基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法与流程
本发明涉及了一种高层建筑风致响应边界评估方法技术领域,尤其是一种基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法的技术领域。
背景技术
传统的高层建筑风致响应的估计方法通常基于平稳风场假设。也就是说,建筑高度的参考风速假定在某风向角下为常数。该方法结合风洞试验可以估计在此风向角下的结构风响应峰值。然而,在台风经过时,建筑物附近的实际风速随时间而变化。对高层建筑在台风过程中的边界行为进行估计,有助于采取必要的措施,如启动振动控制设备或实施疏散计划,以应对台风灾害。
技术实现要素:
本发明实施例提供了一种可以评估非平稳风荷载作用下高层建筑风致响应边界的分析方法,该方法可以根据气象部门提前预测台风风速时变分布的上下边界,结合高频底座测力天平风洞试验数据,能够预测每个时刻结构响应的边界值,对结构工程的防灾减灾具有很好的参考价值。
本发明实施例提供了一种基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法,该边界评估方法包括:
根据风洞测试测得的模型基底气动系数,计算实际建筑物的基底弯矩上下边界;
根据所述实际建筑物的基底弯矩上下边界,计算实际建筑物的结构模态力上下边界;
根据杜哈梅积分和根据所述实际建筑物的单自由度弹簧-质量-阻尼系统,采用杜哈梅积分递推法计算所述实际建筑物的结构响应;
根据实际建筑物的结构模态力上下边界,使用凸模型过程来表示激励,计算所述实际建筑物的结构上下边界响应;
比较所述实际建筑物的结构响应和所述实际建筑物的结构上下边界响应,得到所述实际建筑物的风致响应边界评估结果。
进一步地,在所述根据风洞测试测得的模型基底气动系数,计算实际建筑物的基底弯矩上下边界之前,从气象局获得参考风速的上边界和下边界,所述风速的上边界为vu,所述风速的下边界为vl。
进一步地,在所述从气象局获得参考风速的上边界和下边界之后,根据风洞试验测得模型的基底倾覆力矩;所述风洞试验测得模型在x、y和z方向上的基底倾覆力矩分别为mx、my和mz。
进一步地,在根据风洞试验测得模型的基底倾覆力矩之后,根据所述基底倾覆力矩,计算得到实际建筑物结构的基底倾覆力矩系数,具体为:
所述基底倾覆力矩系数在x、y和z方向的表达式分别如下:
其中,mx、my和mz分别为风洞试验测得模型在x、y和z方向上的基底倾覆力矩,ρ为空气密度,vh为模型参考高度处的平均风速,bmodel为模型特征宽度,hmodel为模型的总高度。
进一步地,所述根据实际建筑物结构的基底倾覆力矩系数,计算实际建筑物的基底弯矩上下边界,具体为:
所述基底弯矩的上下边界在x、y和z方向上的表达式分别为:
mlx=0.5ρvl2bfullhfull2μx,mux=0.5ρvu2bfullhfull2μx(4)
mly=0.5ρvl2bfullhfull2μy,muy=0.5ρvu2bfullhfull2μy(5)
mlz=0.5ρvl2bfull2hfullμz,muz=0.5ρvu2bfull2hfullμz(6)
其中,mux,muy和muz分别为实际结构x、y和z方向上的上边界基底弯矩,mlx、mly和mlz分别为实际结构x、y和z方向上的下边界基底弯矩,vu、vl分别为时变风速的上下边界,bfull为建筑物的特征宽度,hfull为建筑物的总高度。
进一步地,所述根据实际建筑物的基底弯矩的上下边界,计算实际建筑物的结构模态力上下边界,具体为:
所述实际建筑物的结构模态力上下边界在x、y和z方向上的表达式分别如下所示:
flx=αvl2,fux=αvu2,(7)
fly=βvl2,fuy=βvu2,(8)
flz=γvl2,fuz=γvu2,(9)
其中,α=0.5ρbfullhfullμx,β=0.5ρbfullhfullμy,γ=0.5ρbfull2μz;fux,fuy,fuz分别为实际建筑物结构在x,y,z方向上模态力上边界;flx,fly,flz分别为实际建筑物结构在x,y,z方向上模态力下边界。
进一步地,所述根据杜哈梅积分和根据所述实际建筑物的单自由度弹簧-质量-阻尼系统,采用杜哈梅积分递推法计算所述实际建筑物的结构响应,具体为:
根据单自由度弹簧-质量-阻尼系统,得到运动方程:
其中,质量为m,刚度为k,阻尼系数为c,外力为f(t);
根据实际建筑物结构在ti时刻的响应,计算实际建筑物结构在ti+1时刻的响应,具体为:
将实际台风平均风速的时间间隔定义为δt,δt由以下公式得出:
其中,fmodel、dmodel和vmodel分别为模型上的采样频率、迎风面宽度和风速。ffull、dfull和vfull分别为实际建筑物上的采样频率、迎风面宽度和风速;
根据时间间隔δt=ti+1-ti,对应τ时刻的外荷载
ui+1=vui+hfi+1(12)
将公式(12)进行恒等变换和逆向推导,依次得到实际建筑物的
结构位移响应、结构速度响应和结构加速度响应:
xk+1=(hx)1x+(hf)1f,(13a)
其中,(·)i(i=1,2,3)表示矩阵第i行向量,
进一步地,所述根据实际建筑的结构模态力上下边界,使用凸模型过程来表示激励,计算所述实际建筑物的结构上下边界响应,具体为:
使用凸模型过程来表示不确定性激励fi(t),得到如下表达式:
根据凸模型过程理论,得到激励fi(t)的不确定域:
(f-fc)tωf-1(f-fc)≤1(15)
根据实际建筑物的结构响应和激励fi(t)的不确定域将不确定位移响应xk+1转化为如下的最优化问题,由公式(13)和公式(15)得到:
和
其中,f为优化向量;
根据最优化问题,计算最优解f为:
将实际建筑物结构模态力的上下边界作为外部激励,为生成实际建筑物响应的上下边界提供基础条件,根据结合最优化问题和最优解,计算位移响应的上下边界响应、速度响应的上下边界响应、加速度响应的上下边界响应;
所述位移响应的上下边界响应分别可以写为:
所述速度响应的上下边界响应分别可以写为:
所述加速度响应的上下边界响应分别可以写为:
进一步地,所述比较所述实际建筑物的结构响应和所述实际建筑物的结构上下边界响应,得到所述实际建筑物的风致响应边界评估结果,具体为:所述实际建筑物的结构响应只能测试实际建筑物的风速的平均值,所述实际建筑物的结构上下边界响应能测试实际建筑物的每时刻风速上下边界,比较所述实际建筑物的结构响应和所述实际建筑物的结构上下边界响应,得出台风对实际建筑物的破坏程度大小的评估结果。
实施本发明实施例,具有如下有益效果:
本发明实施例提供了一种可以评估非平稳风荷载作用下高层建筑风致响应边界的分析方法,该方法可以根据气象部门提前预测台风风速时变分布的上下边界,结合高频底座测力天平风洞试验数据,能够预测每个时刻结构响应的边界值,对结构工程的防灾减灾具有很好的参考价值。
附图说明
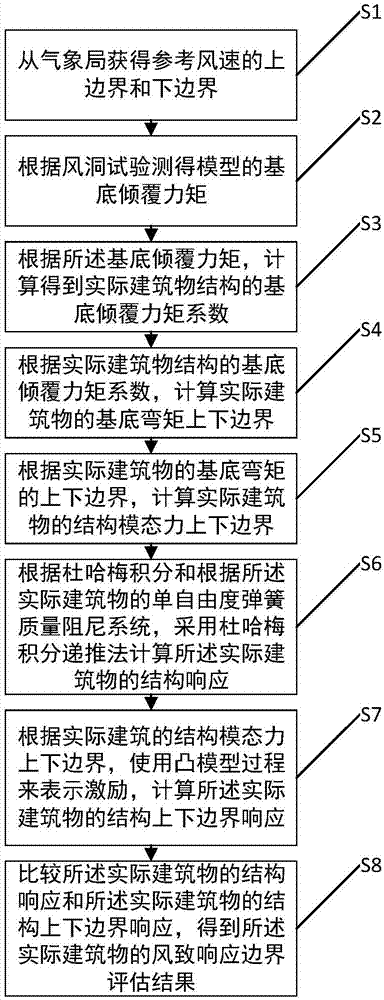
图1为本发明提供一种基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法的一种实施例的流程示意图。
图2为本发明提供的广州某塔风洞试验模型图。
图3为本发明中气象台提供的某次台风的风速图。
图4为本发明提供的台风的风速上下边界图。
图5为本发明提供的由本发明创造提出的方法计算得到广州某塔结构的位移响应上下边界和传统duhamel积分方法得到结构位移响应的对比图。
图6为本发明提供的由本发明创造提出的方法计算得到广州某塔结构的速度响应上下边界和传统duhamel积分方法得到结构速度响应的对比图。
图7为本发明提供的由本发明创造提出的方法计算得到广州某塔结构的加速度响应上下边界和传统duhamel积分方法得到结构加速度响应的对比图。
具体实施方式
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
参见图1,图1为本发明提供的一种基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法的一种流程示意图,如图1所示,一种基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法,包括步骤s1至步骤s8,各步骤具体如下:
步骤s1:从气象局获得参考风速的上边界和下边界,具体为:所述风速的上边界为vu,所述风速的下边界为vl。
步骤s2:根据风洞试验测得模型的基底倾覆力矩,具体为:所述风洞试验测得模型在x、y和z方向上的基底倾覆力矩分别为mx、my和mz。
步骤s3:根据所述基底倾覆力矩,计算得到实际建筑物结构的基底倾覆力矩系数,具体为:所述基底倾覆力矩系数在x、y和z方向的表达式分别如下:
其中,mx、my和mz分别为风洞试验测得模型在x、y和z方向上的基底倾覆力矩,ρ为空气密度,vh为模型参考高度处的平均风速,bmodel为模型特征宽度,hmodel为模型的总高度。
步骤s4:根据风洞测试测得的模型基底气动系数,计算实际建筑物的基底弯矩上下边界,具体为:
所述基底弯矩的上下边界在x、y和z方向上的表达式分别为:
mlx=0.5ρvl2bfullhfull2μx,mux=0.5ρvu2bfullhfull2μx(4)
mly=0.5ρvl2bfullhfull2μy,muy=0.5ρvu2bfullhfull2μy(5)
mlz=0.5ρvl2bfull2hfullμz,muz=0.5ρvu2bfull2hfullμz(6)
其中,mux,muy和muz分别为实际结构x、y和z方向上的上边界基底弯矩,mlx、mly和mlz分别为实际结构x、y和z方向上的下边界基底弯矩,vu、vl分别为时变风速的上下边界,bfull为建筑物的特征宽度,hfull为建筑物的总高度。
步骤s5:根据所述实际建筑物的基底弯矩上下边界,计算实际建筑物的结构模态力上下边界,具体为:
所述实际建筑物的结构模态力上下边界在x、y和z方向上的表达式分别如下所示:
flx=αvl2,fux=αvu2,(7)
fly=βvl2,fuy=βvu2,(8)
flz=γvl2,fuz=γvu2,(9)
其中,α=0.5ρbfullhfullμx,β=0.5ρbfullhfullμy,γ=0.5ρbfull2μz;fux,fuy,fuz分别为实际建筑物结构在x,y,z方向上模态力上边界;flx,fly,flz分别为实际建筑物结构在x,y,z方向上模态力下边界。
步骤s6:根据杜哈梅积分和根据所述实际建筑物的单自由度弹簧-质量-阻尼系统,采用杜哈梅积分递推法计算所述实际建筑物的结构响应,具体为:
根据单自由度弹簧-质量-阻尼系统,得到运动方程:
其中,质量为m,刚度为k,阻尼系数为c,外力为f(t);
根据实际建筑物结构在ti时刻的响应,计算实际建筑物结构在ti+1时刻的响应,具体为:
将实际台风平均风速的时间间隔定义为δt,δt由以下公式得出:
其中,fmodel、dmodel和vmodel分别为模型上的采样频率、迎风面宽度和风速。ffull、dfull和vfull分别为实际建筑物上的采样频率、迎风面宽度和风速;
根据时间间隔δt=ti+1-ti,对应τ时刻的外荷载
ui+1=vui+hfi+1(12)
其中,
cc=2mωn
令p1=-ωn2(a1+ka3)-2ξωn(b1+kb3),p2=-ωn2(a2+ca3)-2ξωn(b2+cb3)
p3=-ωn2ma3-2ξωnmb3,p4=1/m-2ξωna4-ωn2b4
式(12)可以写成:
通过反复利用式(13),可以得到下列递推式:
令t1=0,由公式(10)可以得到:
将公式(14)进行恒等变换,得到如下变换后公式:
结合公式(13)、(14)、(15),进行逆向推导,得到如下公式:
其中,h=hkhk-1…h1γ,令:
将式(17)代入式(16)依次得到实际建筑物的结构位移响应、结构速度响应和结构加速度响应:
xk+1=(hx)1x+(hf)1f,(18a)
其中,(·)i(i=1,2,3)表示矩阵第i行向量,
步骤s7:根据实际建筑物的结构模态力上下边界,使用凸模型过程来表示激励,计算所述实际建筑物的结构上下边界响应,具体为:
使用凸模型过程来表示不确定性激励fi(t),得到如下表达式:
根据凸模型过程理论,得到激励fi(t)的不确定域:
(f-fc)tωf-1(f-fc)≤1(20)
根据实际建筑物的结构响应和激励fi(t)的不确定域将不确定位移响应xk+1转化为如下的最优化问题,由公式(18)和公式(20)得到:
和
其中,f为优化向量;
根据所述最优化问题,建立拉格朗日函数l:
其中,η为拉格朗日乘子;
令
η[ωf-1+ωf-1](f-fc)t+(hf)1=0.(23)
进一步将公式(23)进行简化,得到如下公式:
根据激励fi(t)的不确定域,计算拉格朗日乘子,具体为:将式子(24)代入到式子(20)中,得到:
将公式(25)计算出来的拉格朗日乘子结合到公式(24)中,计算最优解f为:
将实际建筑物结构模态力的上下边界作为外部激励,为生成实际建筑物响应的上下边界提供基础条件,根据结合最优化问题和最优解,结合公式(21)和公式(26),计算位移响应的上下边界响应、速度响应的上下边界响应、加速度响应的上下边界响应;
所述位移响应的上下边界响应分别可以写为:
所述速度响应的上下边界响应分别可以写为:
所述加速度响应的上下边界响应分别可以写为:
步骤s8:比较所述实际建筑物的结构响应和所述实际建筑物的结构上下边界响应,得到所述实际建筑物的风致响应边界评估结果,具体为:所述实际建筑物的结构响应只能测试实际建筑物的风速的平均值,所述实际建筑物的结构上下边界响应能测试实际建筑物的每时刻风速上下边界,比较所述实际建筑物的结构响应和所述实际建筑物的结构上下边界响应,得出台风对实际建筑物的破坏程度大小的评估结果。
在本实施例二中,针对广州某塔来验证本发明提供的一种基于杜哈梅积分与凸模型的高层建筑风致响应边界评估方法。图2为本发明提供的广州某塔风洞实验图。图3为本发明中气象台提供的某次台风的风速图。图4为本发明提供的台风的风速上下边界图。图5为本发明提供的由本发明创造提出的方法计算得到广州某塔结构的位移响应上下边界和传统杜哈梅积分方法得到结构位移响应的对比图。图6为本发明提供的由本发明创造提出的方法计算得到广州某塔结构的速度响应上下边界和传统杜哈梅积分方法得到结构速度响应的对比图。图7为本发明提供的由本发明创造提出的方法计算得到广州某塔结构的加速度响应上下边界和传统杜哈梅积分方法得到结构加速度响应的对比图。
由图5-图7中可以看出,利用本发明提出的杜哈梅-凸模型理论计算等到结构的响应上下边界基本上包络传统杜哈梅方法计算等到的响应,说明了本发明理论的可行性。通过观察响应图,我们还可以明显的得到广州某塔在非平稳台风荷载作用下每个时刻边界响应值的大小,这有助于对高层建筑在台风过程中的边界响应进行估计,有助于采取必要的措施应对台风灾害,如启动振动控制设备或实施疏散计划等。
本发明实施例提供了一种可以评估非平稳风荷载作用下高层建筑风致响应边界的分析方法,该方法可以根据气象部门提前预测台风风速时变分布的上下边界,结合高频底座测力天平风洞试验数据,能够预测每个时刻结构响应的边界值,对结构工程的防灾减灾具有很好的参考价值。
以上所述是本发明的优选实施方式,应当指出,对于本技术领域的普通技术人员来说,在不脱离本发明原理的前提下,还可以做出若干改进和润饰,这些改进和润饰也视为本发明的保护范围。
- 还没有人留言评论。精彩留言会获得点赞!