单层石墨烯本征缺陷下的电导率计算方法与流程

本发明涉及石墨烯电导率计算技术领域，具体涉及一种单层石墨烯本征缺陷下的电导率计算方法。

背景技术：

据2005年nature杂志的一篇报道，石墨烯是一种具有特殊能带结构的零带隙半导体材料，其导带和价带交于一点，即在这一点附近的载流子能量与波矢的色散关系是线性的。其导出的奇妙结果就是在这一点附近载流子的质量为零，可传播微米级的距离而不受散射。石墨烯中载流子可以是电子也可以是空穴，理想状态下其本征载流子迁移率可达10⁵cm²v^-1s^-1级别。且迁移率几乎与温度无关，载流子的有效速度达到了10⁶m/s。石墨烯因其独特的晶体结构和优异的电学性质，在航天科技中应用广泛，不胜枚举。但凡事都有两面性，空间环境因其特殊性，如大温差、各种电离辐射和电磁辐射、中性辐射、微流星、轨道碎片、高/超高真空等，会对在空间工作的器件和材料产生各种影响。石墨烯也不例外，其良好的导电性在空间环境中由于各种空间环境效应的影响也会发生改变。其中最主要的影响就是电离辐射，空间的γ射线辐射，紫外辐射，各种高能粒子辐射等会对石墨烯导电性产生各种性质的影响。例如紫外辐射，近日空间环境中，紫外辐照是较为重要的因素之一。波长短于300纳米的所有紫外辐照，虽然只占有太阳总辐照能量的1％左右，但作用很大。紫外线的光量子能破坏石墨烯的碳碳键，引起化学结构变化，造成能态密度、电荷密度改变，进而影响其导电性。空间辐照环境主要来自地球辐射带、太阳宇宙射线、银河宇宙射线等，主要成分是电子、质子、少量重离子和γ射线，它们构成了航天器轨道上的辐射环境。高能粒子会轰击石墨烯的晶胞结构，使其产生位移缺陷、空位缺陷和吸附缺陷等，从而改变其电子能态分布等特性，影响其导电性。同样γ射线也会破坏石墨烯的键，从而影响其导电性。

目前通常采用实验检测的方法获得石墨烯的电导率，然而，本征缺陷的数量本来就及其微小，随着石墨烯生长工艺的不断改进，其本征缺陷会越来越少，超出了实验测量极限；因此，需要采用新的方法研究单层石墨烯出现本征缺陷后引起的电导率变化。

技术实现要素：

有鉴于此，本发明提供了一种单层石墨烯本征缺陷下的电导率计算方法，利用第一性原理计算理论，计算出完美石墨烯晶胞结构出现缺陷之后的结构与电子特性的改变，进而得到电导率变化情况。

本发明的单层石墨烯本征缺陷下的电导率计算方法，包括如下步骤：

步骤1，构建不同类型本征缺陷晶胞结构模型，利用第一性原理，计算各类型本征缺陷晶胞的体系总能，最小体系总能所对应的本征缺陷晶胞即为最稳定的本征缺陷晶胞结构；

步骤2，建立步骤1确定的最稳定的本征缺陷晶胞结构的完备晶胞β1；同时建立单层石墨烯完美晶胞结构的完备晶胞β0作为对照；

步骤3，利用第一性原理，分别计算完备晶胞β1和完备晶胞β0的电荷密度分布信息以及电子能态密度分布信息；

步骤4，将两个完备晶胞β1、β0的电子能态密度分别做积分处理，根据两个完备晶胞的电子能态密度积分的变化值计算单层石墨烯在发生本征缺陷后的电导率变化量。

进一步的，所述步骤4中，两个完备晶胞的电子能态密度分别在费米面正负3个kt范围内做积分，得到晶胞β0和晶胞β1的积分能态密度，其中，k为玻尔兹曼常数，t为开氏温度。

进一步的，所述步骤1中，针对各类型本征缺陷晶胞结构模型，首先固定非缺陷原子，对晶胞剩余其他原子进行位置弛豫，得到最稳定构型；然后固定最稳定构型所有原子，对整个晶胞结构再进行一次弛豫，得到对应本征缺陷晶胞的体系总能。

进一步的，所述步骤4中，在计算完备晶胞β1和β0的电子能态密度分布信息时，将石墨烯的褶皱结构作为非线性因素引入第一性原理计算中。

有益效果：本发明从真实物理过程和基本物理原理出发，详细分析了石墨烯本征缺陷对其电导率的影响规律。相对于实验测量，本发明不存在实验测量误差的影响。同时，通过改变不同的计算输入，可以分析不同石墨烯本征缺陷类型、数目对其电导率的影响，相对于实验测量效率更高。最重要的是，理论计算分析可以突破实验测量精度的限制。故通过本发明，对于石墨烯电导率的分析更准、更精且更有效。本发明可为石墨烯及石墨烯基的功能材料、器件及航空航天载荷在辐射环境下电学性质的改变研究提供可靠的技术支撑。

附图说明

图1为点缺陷的tem图像和计算得到的原子排布结构图。

图2为单空穴缺陷的tem图像和计算得到的原子排布结构图。

图3为三种已经观察到的多重空穴缺陷的tem照片和其原子排布结构图。

图4为三种典型的面外碳原子引入缺陷。

图5为本发明实施例中所采用的计算软件vasp及计算所用超级计算机组示意。

图6为本发明实施例中构建vasp计算输入结构文件的商业模拟应用软件materiasstudio界面示意。

图7为本发明实施例中构建的石墨烯完美晶胞结构与各类本征缺陷结构。

图8为本发明实施例中构建的石墨烯完美晶胞结构β0与各类本征缺陷结构α1～α4晶胞常数优化后的相对体系总能。

图9为本发明实施例中计算得到的β1和β0能态密度分布与积分能态密度对比图。

图10为本发明方法步骤流程图。

具体实施方式

下面结合附图并举实施例，对本发明进行详细描述。

本发明提供了一种单层石墨烯本征缺陷下的电导率计算方法，根据第一性原理理论，结合商用计算程序vasp对石墨烯本征缺陷建立结构模型，计算分析其结构与电子特性的变化。

第一性原理在石墨烯研究的初期、高峰、直至将来都是强有力的不可或缺的重要手段之一。这是因为石墨烯独特的结构和电子特性就是因其纳米尺度的结构特点带来的，而第一性原理就是从晶体结构出发，不含一切拟合参数因子来推导出物质的宏观性质。要分析辐射损伤、缺陷对石墨烯导电性的影响，就要从物质导电性的基本概念出发，从固体物理角度来分析晶体导电性的由来。如前所述，石墨烯优异的导电性主要由其能带中狄拉克点附近的电子的弹道输运形成，在狄拉克点，导带低和价带顶重合，能带具有金属性特征，可以用固体物理中的金属电子论理论来分析其电导率的特点。本发明可直接应用到石墨烯相关空间材料及器件的设计、研制、失效分析等方面。

本发明获取单层石墨烯在发生本征缺陷时电导率变化的步骤如下：

步骤1，首先确定利用第一性原理计算软件vasp的计算输入设置。

本发明是利用第一性原理计算单层石墨烯本征缺陷下的结构与电子特性的变化，从而得到单层石墨烯本征缺陷下的电导率变化；本实施例是直接利用软件vasp进行第一性原理的计算，该软件的计算精度高、输入输出可视化、操作方便；但本发明并不限于该软件，只要是能够基于第一性原理，构建晶胞，并实现对晶胞的结构以及电子特性的计算即可。

在vasp中：对于离子、原子等基本粒子之间的相互作用通过赝势来进行描述，即通过平面波扩增投影算法来进行描述粒子之间的相互作用；带电粒子之间的交换相互作用是通过广义梯度近似来进行描述。在进行不同的计算步骤时，设置的monkhorst-pack网格大小逐渐改变。在平面波矢量计算时，本发明采取的截断能初始范围为200至700毫电子伏特，通过优化得到最佳截断能取值为360毫电子伏特。采用这样的截断能可以在近似下达到计算精度的需求。

步骤2，建立石墨烯本征缺陷的晶胞结构模型并确定缺陷晶胞结构的晶胞常数。

室温下，完美单层石墨烯的晶胞常数是已知量，但为了保持模拟计算的统一性，需通过计算确定出完美单层石墨烯在常温下的晶胞常数：在上述的计算设置下，利用vasp构建石墨烯的六角蜂巢状的模型，计算出不同晶胞常数对应的晶胞体系能量，取能量最低点为最概然的晶胞常数。以此晶胞常数为基础，进行后续计算。

其次需要构建石墨烯本征缺陷的晶胞结构模型。大量已知实验和理论已经确定石墨烯各类本征缺陷为：点缺陷，单空穴缺陷，多重空穴缺陷，线缺陷和面外碳原子引入缺陷。

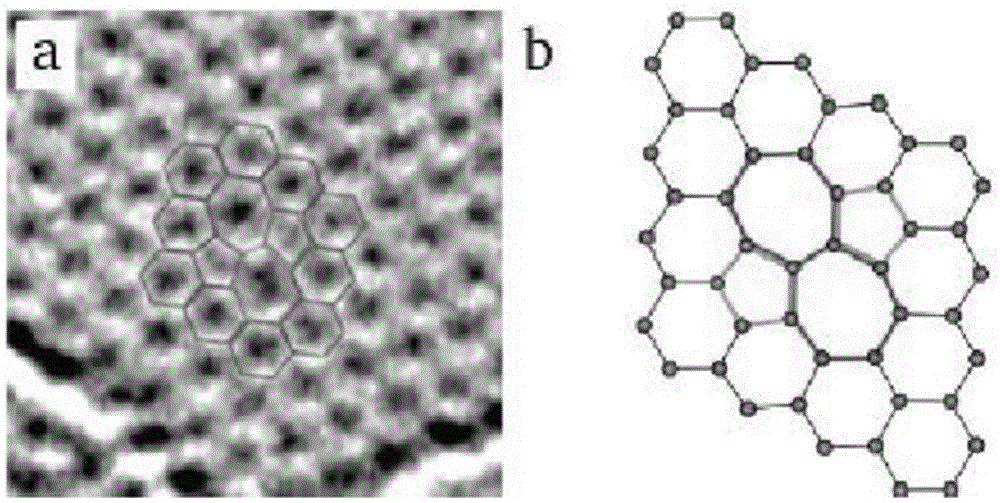
其中，点缺陷：石墨烯的点缺陷是由于c-c键的旋转而形成的，因此该缺陷的形成并没有使石墨烯分子内发生碳原子的引入或者移除，也不会产生具有悬键的碳原子。这种缺陷的形成能大约为5ev。点缺陷可以由于电子束轰击或者在高温环境中快速冷却产生。图1为点缺陷的tem图像和计算得到的原子排布结构图。

单空穴缺陷：如果在连续排列的碳六元环中丢失一个碳原子，石墨烯上就会形成单空穴缺陷。图2为单空穴缺陷的tem图像和计算得到的原子排布结构图。很显然，一个碳原子的丢失必然造成与本来与其相连的三个共价键断裂，其结果是形成了三个悬键。

多重空穴缺陷：单空穴缺陷的基础上，如果再丢失一个碳原子，就会产生多重空穴缺陷，图3展示了三种已经观察到的多重空穴缺陷的tem照片和其原子排布结构图。不难理解，如果能使碳原子丢失的外能量持续存在(如高能电子束轰击)，石墨烯片层上将持续丢失碳原子，多重空穴缺陷会变得更加复杂。

线缺陷：在使用化学气相沉积方法制备石墨烯的过程中，石墨烯会在金属表面的不同位置开始生长，这样生长的随机性导致不同位置生长的石墨烯会有不同的二维空间走向，当这些石墨烯生长到一定大小后，开始发生交叉融合，融合的过程中由于起始晶取向的不同开始出现缺陷，这种缺陷通常呈现线型。一般在石墨烯生长过程中产生。

面外碳原子引入缺陷：单空穴和多重空穴缺陷形成时产生的丢失碳原子，并不一定完全脱离石墨烯，很多时候，这些碳原子在脱离原始碳六元环后，形成了离域原子而在石墨烯表面迁移。当其迁移至石墨烯某一位置时，会形成新的键。这样的缺陷将破坏该区域原有的平面结构，形成立体结构。图4是三种典型的面外碳原子引入缺陷，a～c显示了这样缺陷的空间排布，d～e为对应的丢失碳原子的引入位置。由于面外碳原子引入缺陷或者具有非常快的迁移速度，或者具有很高的形成能量，实际试验中，很难通过各种显微技术(spm、tem)捕捉到，目前还没有见到有关面外碳原子引入缺陷的观测报道。

针对上述本征缺陷情况，分别构建各类本征缺陷下的晶胞结构模型，并构建各缺陷晶胞结构模型所对应的晶胞；然后利用第一性原理计算各类本征缺陷晶胞的体系总能；最低体系总能所对应的本征缺陷晶体结构即为最稳定的情况，也就是最可能的本征缺陷晶体结构模型。具体如下：

在materiasstudio中构建的石墨烯的完美晶胞结构β0与本征缺陷晶胞结构αi(i＝1,2,3,4....)。将结果输出为vasp计算的结构输入文件poscar，在vasp中首先对β0进行弛豫，得到完美石墨烯的晶胞结构常数。其次对晶胞αi(i＝1,2,3,4....)进行结构弛豫，在vasp的输出文件outcar中，可以得到晶胞αi的体系总能。其中选取能量最低值，即为各类缺陷结构的真实晶胞常数，即得到最为稳定的本征缺陷晶胞结构α0。

步骤3，建立完备单层石墨烯本征缺陷晶胞β1。通过vasp依照计算流程依次对β1和β0进行结构优化、静态计算与体系能态密度计算。

具体的，根据得出的石墨烯缺陷结构的晶胞常数信息，构建完备石墨烯本征缺陷晶胞。接下来对完备晶胞β1和完备晶胞β0进行第一性原理vasp计算，得到完备晶胞β1和完备晶胞β0的电荷分布信息以及电子能态密度分布信息：

在结构计算的vasp输出文件中，将contcar文件再次作为结构输入文件，固定晶胞的所有原子，对整个体系做一次自洽的静态计算，即可以得到整个体系的电荷分布信息。

此时，将上一步计算结果中代表电荷分布信息的文件chg和chgcar作为vasp的输入文件，对整个体系在进行一次自洽计算，就得到了体系的电子能态密度分布信息，反映在vasp输出文件的doscar中。

步骤4，结合vasp计算结果，分析完备晶胞β和完备晶胞β0的电导率变化情况。

具体的，首先对β1和β2的电子能态密度进行分析。这里需要做出体系能态密度在费米面附近的积分能态密度，作为下述理论推导的输入数据。

具体为：根据前述分析体系的电导率采用金属电子论：

当给金属施加一个恒定电场e后，实际上在飞秒量级的时间内就会形成一稳定电流密度j，服从欧姆定律：

j＝σe

其中，σ为电导率。

稳定的电流的本质反映了，在恒定外场下，电子达到一个新的定态统计分布，这种定态分布也可以用一个与平衡时相似的分布函数f(k)来描述，一旦确定了分布函数f(k)，就可以直接计算电流密度。

众所周知，在简单的电子理论中，解释欧姆定律的主要物理基础是：

(i):电子在电场e作用下加速；

(ii):电子由于碰撞失去定向运动

对于(i)来说，由能带理论可以证明，在e的作用下，所有的电子状态变化服从：

其中，k为电子波矢，t为时间，e为外加电场，q为基本电荷量，h为玻尔兹曼常数。

而对于(ii)，假定电子有一定的碰撞自由时间τ，一旦遭受碰撞就完全丧失在电场中所获得的定向运动。为了定量研究电子运动理论，引入关于电子输运分布函数的微分方程——波尔兹曼方程。波尔兹曼方程是从考察电子输运分布函数如何随时间变化而确立的，电子输运分布函数的变化有两个来源：

i:由外界条件所引起的统计分布在k空间的“漂移”

ii:碰撞，由于晶胞原子的振动，或者是杂质的存在等具体原因，电子不断地发生从一个状态k到另一个状态k′的跃进，电子态的这种变化叫做散射。假设碰撞的末态和初态可以简化为b和a，则波尔兹曼方程可以简化为：

为f(k)的梯度；碰撞项b-a的积分包含着未知的分布函数，因此，波尔兹曼方程是一个积分-微分方程式，在一般情况下，不能得到简单的解析形式解，在实际中，一个广泛的近似如下：

其中f0是平衡时的费米函数，f＝f(k)，τ为引进的一个参量，叫做弛豫时间。利用能带的基本关系式：最后可得电流密度公式为：

把上式用分量表示：

最后得到电导率：

值得注意的是，上式出现表明，积分的贡献主要来自e＝ef附近，也就是，电导率主要决定于费米面e＝ef附近的情况。假设金属导带电子基本可以用单一的有效质量m^*描述：

将积分展开，忽略高次项，金属电导率最终可以写成：

其中，σ0代表张量σαβ的标量值。石墨烯本征缺陷对其电子迁移率(弛豫时间)τ(ef)和电子有效质量m^*基本无影响，从而对于体系电导率σ0的影响因素就归结到电子体密度n。值得注意的是，此时的n为体系费米面附近价电子的数密度。对于石墨烯完美晶胞或者缺陷晶胞结构来说，整个体系的电子分布函数不变，故结合上述电子能态密度计算结果，对β1和β0做其费米面附近的电子能态密度做积分再比较，就可得出体系的电导率变化情况。其中，k为玻尔兹曼常数，t为开氏温度，费米面正负3个kt范围内的电子能态密度可以很好的反映出晶体的电导特征。

在计算完备晶胞β1和β0的电子能态密度分布信息时，将石墨烯的褶皱结构作为非线性因素引入第一性原理计算中，即在vasp计算的输入文件incar里打开自旋轨道耦合值；如此，计算结果更为精确。

本发明为石墨烯本征缺陷对其电导率的影响情况提供了一个理论分析方案，弥补了实验测量极限的不足。

本发明的结果还可作为理论基础，来进一步研究石墨烯非本征缺陷对其电导率的影响规律。

下面结合具体例子进行说明：

图5为本发明计算采用的第一性全量子计算商业软件vasp，其版本为vasp.5.3.5，所用超级计算机组为上海超算中心。使用赝势为paw-gga。

单层石墨烯的晶格常数是已知的，但为了保证本研究的一致性，利用第一性原理计算工具vasp，计算了单层石墨烯的完美的晶格常数，首先在商业应用软件materiasstudio中构建其晶胞，如图6。

将结构信息作为输入，写入vasp的结构输入文件poscar，通过晶格弛豫，计算出单层石墨烯的晶胞基矢长度为a＝0.247nm，而实验测得，室温(300k)下，单层石墨烯的晶胞基矢长度为0.246nm。故验证了采用的计算工具是较为吻合实际情况的。

当单层完美石墨烯晶胞出现本征缺陷时，前面已经讨论，共有点缺陷，单空穴缺陷，多重空穴缺陷，线缺陷和面外碳原子引入缺陷五种。根据分析，线缺陷和面外碳原子引入缺陷属于石墨烯生长过程中产生的工艺缺陷，随着石墨烯生长工艺的不断进步这类缺陷可以避免。那么需要对其它几类缺陷进行晶胞构建：单空位缺陷、双空位缺陷、stone-wales缺陷和555-777缺陷，如图7，分别为石墨烯完美晶胞β0，石墨烯不同类型结构缺陷晶胞αi(i＝1,2,3,4)。通过商业应用软件materiasstudio导出β0和αi(i＝1,2,3,4)的vasp结构输入文件poscar。代入vasp进行晶格弛豫，得出各类晶胞的最稳定结构和与之对应的体系最低晶胞能量，并进行了对比，如图8。可见，单空位缺陷为石墨烯最为可能形成的本征缺陷，因其体系能量相对其余缺陷结构最低，即所需外界扰动的能量最小。故选取石墨烯单空位缺陷为接下来计算的缺陷结构晶胞β1。

根据上述计算结果，对单层石墨烯完美结构晶胞β0和单空位本征缺陷晶胞β1进行体系能态密度计算。

在计算体系能态密度之前，需要对β0和β1进行结构弛豫和自洽的静态计算。所谓静态自洽计算，即为固定每个原子的位置，从最基本的薛定谔方程出发，对整个体系进行不断的自我迭代计算，最后在所设置的精度范围内，得到整个体系的最置信组态。

前面的分析表明对于β0，其电导率标量值σ0计算公式为：

产生单空位缺陷后对整个体系的价电子来说，其电子迁移率(弛豫时间)和电子有效质量不发生改变，从而对于体系电导率的影响因素就归结到电子体密度n。且n为体系费米面附近价电子的数密度。

在上一步静态计算的结果中，得到了晶胞β0和β1的自洽电荷密度，体现在vasp的输出文件chgcar和chg中，接着上一步，对β0和β1进行能态密度计算。这时候，设置输入文件incar的时候，里面的ichagr＝2就要改为icharg＝11，代表采用已经计算好的输入文件chgcar和chg，这时候再进一步加大kpoints的计算精度，同时依旧固定原子的坐标。计算得到了β0和β1的能态密度分布与积分能态密度，结果如图9所示。

通过对费米能级附近的积分态密度进行累加再做加权平均比较，得到单空位缺陷晶胞β1较对照组完美晶胞β0积分能态密度减小量为3％。对于吸附前后来说，整个体系的电子分布函数不变，故体系费米面附近价电子的数密度n，也就是体系电导率减小量亦为3％，与文献报道石墨烯空位缺陷的电子输运性能下降5％左右的实验测量结果较为吻合。

建立石墨烯本征缺陷结构的晶格构型模型；利用第一性原理计算软件vasp确定缺陷结构最为稳定的晶格常数；根据得出的晶格结构缺陷模型，建立第一性原理的计算晶胞；利用第一性原理计算软件vasp计算晶胞的晶胞结构、静态情形、能态密度；根据计算结果，理论分析并推导出石墨烯出现本征缺陷之后的电导率变化情况。该方法创新性高，基于严谨理论分析手段拓展了实验测量，即适用于石墨烯缺陷对其电导率的极为敏感的影响分析，尤其适用于当实验中难于确定石墨烯本征缺陷类型时。在本发明的基础上，继续研究并系统建立各类石墨烯缺陷对其电导率影响规律，在基于石墨烯的材料和器件的航空航天辐射环境下应用评价中将有巨大应用价值。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。