一种基于主成分分析法的硬件木马检测方法与流程

本发明涉及一种集成电路的硬件木马检测方法，尤其涉及一种基于主成分分析法的硬件木马检测方法，属于集成电路安全性领域。

(二)

背景技术：

由于集成电路工艺的精密性和复杂性，其制造过程需要在专业的芯片制造工厂内完成。因此，集成电路的研发工作一般都是由设计师完成电路的设计，然后将包含电路版图信息的文件交给芯片代工厂，必要时甚至需在其它国家加工，这使加工环节脱离安全控制，为硬件木马攻击提供了可能，也使集成电路面临硬件木马的威胁。考虑到集成电路常用与通信工程与系统控制，硬件木马严重威胁集成电路的使用安全。

侧信道分析技术是一种利用集成电路在工作时的侧信道信号(例如电流、电路延时或电磁信号等)来检测硬件木马的方法。考虑到被植入的硬件木马电路会对原有目标电路的一些侧信道信号产生影响，通过观察集成电路的侧信道信号并与金片的侧信道信号比较，可以检测出集成电路是否被植入硬件木马。基于侧信道分析的硬件木马检测技术的最大优点是可以是硬件木马在没有被触发的情况下被检测出来。且在未知硬件木马的类型时，基于侧信道分析的检测方法较为通用，且准确度较高。

但是这种检测方法也有一定的局限性，当待测集成电路的总体规模较大，且被植入的硬件木马所占面积较小时，侧信道信号的变化较小。且考虑到集成电路本身制造工艺导致的偏差和测试过程中的引入的噪声也会使侧信道信号产生变化。因此为了减小工艺偏差及测量噪声对硬件木马检测的影响，现已有学者开始尝试对信号进行处理。目前，主要有以下两类处理方法：一类是对侧信道信息进行整体处理，通过将侧信道信息投影到特征空间实现信号主特征的提取和数据的压缩，再用少量的主特征实现检测。另一类是对信号微弱差异进行识别，实现对信号细节的观察与处理。两类检测方法均能实现一定程度的硬件木马检测，但是对数据处理的程度仍旧有限，导致检测精度还有提高空间，所以针对硬件木马检测的数据特点进行研究，探索更加全面有效的数据处理方法将十分有必要。

主成分分析法是一种可以提取原始数据样本中的特征向量，对数据进行降维优化的统计学方法。它以原有数据的均方差最小为目标，挑选出最能体现原有数据样本特征的投影矩阵，并使数据在分析时，由于主成分分析产生的误差最小。利用主成分分析法可以实现选取并分析原有数据的有效成分，可以有效提高数据的信噪比，并降低数据结构的复杂程度，减小数据中的噪声和冗余对数据特征的影响。

侧信道检测方法对于检测面积较小的硬件木马具有一定的局限性，因此需要利用数据降维算法降低工艺偏差对检测效果的干扰，同时区分被植入和未被植入硬件木马的功率数据。现有的仅利用主成分分析法(即pca的检测方法)无法检测面积小于1％的硬件木马。针对这一问题，本文提出了基于pca和马氏距离的硬件木马检测方法，在pca的基础上利用马氏距离进一步区分被植入和未植入硬件木马的功率数据，进而提高检测方法的准确度。本方法在主成分分析法的基础上，利用马氏距离对信号进一步分离，处理和分析电源电流数据，有效分离木马信号与目标信号，增加检测的准确性。

(三)

技术实现要素：

1.目的：

本发明的目的是为了提供一种基于主成分分析法的硬件木马检测方法，它能解决目前基于侧信道分析的硬件木马检测方法无法检测面积小于1％的硬件木马的问题。

2.技术方案：

本发明提出一种基于主成分分析法的硬件木马检测方法，先记录不同时钟频率下母本数据、训练样本和待测样本的电源电流并分别形成样本集，然后对母本数据进行主成分分析并计算训练样本和待测芯片的特征矩阵，再计算训练样本和待测芯片的马氏距离，最后判断待测芯片的马氏距离是否超出了训练样本的统计分布，若待测样本的马氏距离超出了训练样本的分布范围，则待测芯片含有硬件木马；若待测样本的马氏距离在分布范围内，则待测芯片不含有硬件木马。

本发明一种基于主成分分析法的硬件木马检测方法，该方法包括以下步骤：

步骤一：在芯片运行频率的附近选取q个频率作为外部输入的时钟频率，并记录q个不同时钟频率下m+t个无木马芯片和待测芯片的电源电流；不同时钟频率下芯片的电源电流不同，通过记录m个无木马芯片在不同时钟下的电源电流值可以形成母本数据集a；记录t个无芯片木马的电源电流，形成训练样本集b；记录待测芯片的电源电流值形成待测样本数据集d；

步骤二：对母本数据集进行主成分分析，计算母本数据协方差矩阵c的特征值，其具体实现方式如下：

式中：c为协方差矩阵，表示矩阵内部各个组成元素之间的相关性；

a为m个无木马芯片在不同时钟下的电源电流值形成的母本数据集；

p^tcp＝λ

p为c的特征向量矩阵，λ为特征值矩阵，按照从大到小的顺序排列特征值及其对应的特征向量；按顺序计算各成分对矩阵特征的贡献率，选取前k个成分的贡献率之和大于一个定值，对应的k个特征向量构成的投影变换矩阵pm×k；

对特征值进行从大到小排序，选取贡献率较高的前k个特征值对应的特征向量形成特征向量矩阵pm×k；

步骤三：计算训练数据的特征投影矩阵y1，待测样本的特征投影矩阵y2，其具体实现方式如下：

y1＝bt×q×pq×k

y2＝d1×q×pq×k

式中：b为t个无芯片木马的电源电流形成的训练样本集；

d为待测芯片的电源电流值形成的待测样本数据集；

将b、d投影到p得到降维后的主成分矩阵y1、y2，维度由q降到k，同时还能够有效的反应原始数据的主要特征；

步骤四：计算训练数据的马氏距离z1，及待测样本与母本的马氏距离z2，其具体实现方式如下：

其中，代表矩阵a的重心，的表达式如下：

∑是矩阵a的协方差矩阵：

式中：ai是母本数据集a中第i个主成分组成的向量；

步骤五：统计训练数据的马氏距离分布并判断待测样本的马氏距离是否超出了训练数据的分布范围，其具体实现方式如下：

考虑到工艺偏差的分布为随机分布，且马氏距离不改变分布情况，利用区间估计，计算训练样本的马氏距离的置信区间。均匀分布的置信区间计算公式如下：

ul＝m+a×st

ul＝m-a×st

其中，ul为置信上限，ll为置信下限；m为训练样本的马氏距离均值，st为训练样本的马氏距离标准差；a的取值与置信度有关，当置信度为95％时，a＝1.96；

若待测样本的马氏距离超出了训练样本的分布范围，则待测芯片含有硬件木马；若待测样本的马氏距离在分布范围内，则待测芯片不含有硬件木马；

通过以上步骤，就能利用主成分分析法和马氏距离判别检测芯片中是否含有硬件木马；在主成分分析法的基础上，利用马氏距离对信号进一步分离，处理和分析电源电流数据，有效分离木马信号与目标信号，增加检测的准确性。

其中，在步骤二中所述的“主成分分析”，是指计算母本数据协方差矩阵c的特征值，其具体实现方式如下：

式中：c为协方差矩阵，表示矩阵内部各个组成元素之间的相关性；

a为m个无木马芯片在不同时钟下的电源电流值形成的母本数据集；

p^tcp＝λ

p为c的特征向量矩阵，λ为特征值矩阵，按照从大到小的顺序排列特征值及其对应的特征向量；按顺序计算各成分对矩阵特征的贡献率，选取前k个成分的贡献率之和大于一个定值，对应的k个特征向量构成的投影变换矩阵pm×k。

其中，在步骤三中所述的“计算训练数据的特征投影矩阵y1，待测样本的特征投影矩阵y2”，其具体实现方式如下：

y1＝bt×q×pq×k

y2＝d1×q×pq×k

将b、d投影到p得到降维后的主成分矩阵y1、y2，维度由q降到k，同时还能够有效的反应原始数据的主要特征。

其中，在步骤四中所述的“计算训练数据的马氏距离z1，及待测样本与母本的马氏距离z2”，其具体实现方式如下：

其中，代表矩阵a的重心，的表达式如下：

∑是矩阵a的协方差矩阵：

式中：ai是母本数据集a中第i个主成分组成的向量；

其中，在步骤五中所述的“统计训练数据的马氏距离分布”，其具体实现方式如下：

考虑到工艺偏差的分布为随机分布，且马氏距离不改变分布情况，利用区间估计，计算训练样本的马氏距离的置信区间；均匀分布的置信区间计算公式如下：

ul＝m+a×st

ll＝m-a×st

其中，ul为置信上限，ll为置信下限；m为训练样本的马氏距离均值，st为训练样本的马氏距离标准差；a的取值与置信度有关，当置信度为95％时，a＝1.96。

3.优点及功效：

本发明提供一种基于主成分分析法的硬件木马检测方法，该发明的优点是：

(1)提供了硬件木马的检测流程

(2)主成分分析法的基础上，利用马氏距离对信号进一步分离，处理和分析电源电流数据，有效分离木马信号与目标信号，增加检测的准确性。

(四)附图说明：

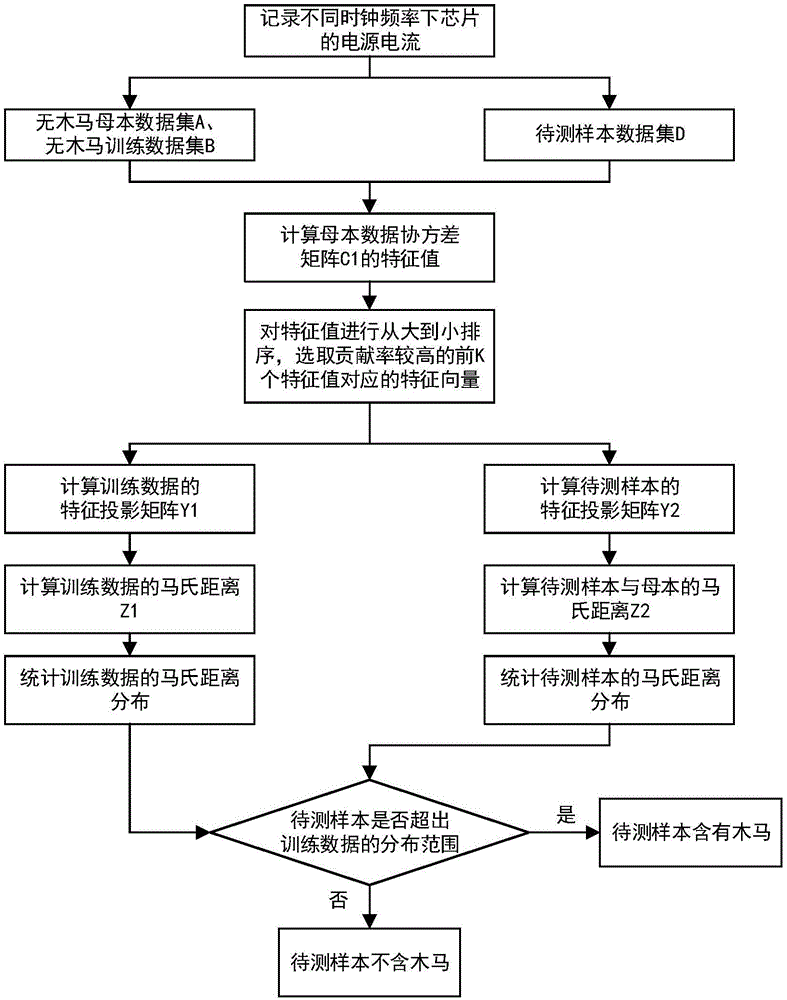
图1本发明所述方法流程图。

图2待测芯片与训练样本特征投影对比图。

图3待测芯片与训练样本马氏距离对比图。

(五)具体实施方式：

本发明选取xilinx公司的xc6slx9型fpga作为硬件木马的攻击芯片。xc6slx9为平面封装的塑封器件。共选取201个样品作为检测对象，并对样品进行编号，其中无硬件木马芯片200个，待测芯片1个。本案例的硬件木马在植入目标电路后占用了16个寄存器，13个逻辑单元，而xc6slx9型fpga具有11440个寄存器，5720个逻辑单元，硬件木马的资源占有率远低于1％，属于面积较小的硬件木马。结合具体的实际案例，对本发明所述的一种基于主成分分析法的硬件木马检测方法进行详细说明。

本发明一种基于主成分分析法的硬件木马检测方法，其流程图如图1所示，具体实施步骤如下：

步骤一：改变外部输入的时钟频率，并记录23个不同时钟频率下200个无木马芯片和待测芯片的电源电流；不同时钟频率下芯片的电源电流不同，通过记录100个无木马芯片在不同时钟下的电源电流值可以形成母本数据集a；记录另100个无芯片木马的电源电流，形成训练样本集b；记录待测芯片的电源电流值形成待测样本数据集d；

步骤二：对母本数据集进行主成分分析；对特征值进行从大到小排序，选取贡献率较高的前10个特征值对应的特征向量形成特征向量矩阵p100x23；

步骤三：计算训练数据的特征投影矩阵y1，待测样本的特征投影矩阵y2，见图2；

步骤四：计算训练数据的马氏距离z1，及待测样本与母本的马氏距离z2，见图3；

步骤五：统计训练数据的马氏距离分布并判断待测样本的马氏距离是否超出了训练数据的分布范围；在置信区间为95％的情况下，n为1.96，训练样本的马氏距离区间估计值为(2.7066,9.4339)。待测芯片的马氏距离为15.1044，该芯片中被植入了硬件木马。

通过以上步骤，就能利用主成分分析法和马氏距离判别检测芯片中是否含有硬件木马。