一种基于四维陈氏超混沌系统与K-means聚类的图像加密方法与流程

本发明涉及图像处理领域，更具体地，涉及一种基于四维陈氏超混沌系统与k-means聚类的图像加密方法。

背景技术：

随着互联网和信息技术的快速发展，各种数字信息不断地通过电子设备传播。在数字信息中，数字图像是一种比较直观生动的信息。由于数字图像可能涉及国家安全、商业利益和个人隐私等，因此，需要对其进行加密保护，特别是在传输过程中。当前，主流的数字图像加密方案是基于混沌理论的置乱-扩散方案，即利用混沌系统生产的混沌序列，先对图像像素进行空间位置置乱，得到置乱图像，然后再对置乱图像进行像素值扩散，最后得到加密密文。

基于混沌理论的置乱-扩散图像加密方案总体上具有较好的安全性，但也存在一些问题，主要表现在以下几个方面。首先，基于低维混沌系统的秘钥仍存在被破译的风险，特别是对于一维混沌系统。其次，对于高维混沌系统而言，其具有较高的安全性，但通常也具有较高的时空复杂性，影响了图像加解密的效率，特别是当频繁产生混沌序列的时候。最后，通过混沌系统生成的混沌序列多数没有经过统计测试，其伪随机性有待检验，因此，加密安全需要进一步提升。

技术实现要素：

针对当前加密方案的不足，本发明提出一种基于四维陈氏超混沌系统与k-means聚类的图像加密方法，以进一步提升基于混沌系统的数字图像加密安全同时兼顾加密效率，为数字图像信息安全技术领域提供重要的应用基础。

为了实现上述目的，本发明的技术方案为：

一种基于四维陈氏超混沌系统与k-means聚类的图像加密方法，采用高维连续超混沌系统——四维陈氏系统来生成混沌序列，保障算法具有更大的密钥空间，并通过k-means聚类算法对陈氏系统产生的混沌序列进行0,1化处理，得到伪随机性能良好的二值序列(通过usnist统计测试)。其次，根据明文图像的位(bit)面分解的性质，设计高效的置乱算法，并在置乱与扩散之间增加中间结果分存环节，提升加密安全。最后，改进传统的线性扩散函数，利用伪随机二进制序列产生的扩散矩阵，对初步密文像素执行线性双向扩散，进一步提升系统抵御差分分析攻击的性能。

优选的，上述方法具体为：

采用四维超混沌陈氏系统来生成混沌序列，并通过k-means聚类算法对四维超混沌陈氏系统产生的混沌序列进行0,1化处理，得到伪随机二进制序列，其过程为：

第一步，已知四维超混沌陈氏系统为：

其中，x,y,z,w为关于时间t的未知量，dx/dt,dy/dt,dz/dt,dw/dt为未知量关于时间t的导数，a,b,c,d,r为控制参数；

当参数a＝35,b＝3,c＝12,d＝7,r＝0.6时，系统(1)进入混沌状态；给定初值x＝0.1,y＝-0.1,z＝0.1,w＝-0.1，时间步长取δt＝0.001，利用runge-kutta算法求解方程(1)，分别舍弃最初的部分值，得到四个长度皆为l的实值混沌序列，为：x＝{x1,x2,...,xl},y＝{y1,y2,...,yl},z＝{z1,z2,...,zl},w＝{w1,w2,...,wl}

记序列x＝{x1,x2,...,xl}的最小值和最大值分别为xmin,xmax，把区间[xmin,xmax]等分成t个子区间，则t-1个等分点为i＝1,2,...,t-1，令

下面利用k-means算法对序列x进行聚类处理，形成t个类，并设置t个类的初使类中心为i＝1,2,...,t，经过k-means算法处理后得到的t个类记为si，相应的类中心分别为νi，i＝1,2,...,t，

第三步：把每个类中的元素减去对应的类中心后，得到集合即i＝1,2,...,t，接着利用符号函数(2)对集合进行0、1化处理后得到二进制集合即

最后合并集合得到伪随机二进制序列

第四步：类似地，按照第二、三步两步对混沌序列y＝{y1,y2,...,yl},z＝{z1,z2,...,zl},w＝{w1,w2,...,wl}进行同样的处理，分别得到二进制序列

第五步：利用x',y',z',w',根据(3)式，得到最终的伪随机二进制序列b＝{b1,b2,b3,b4,...,b4l-1,b4l}；

上式b41就是b4,b42就是b8，以此类推，下标数字是乘积关系。

根据明文图像的位(bit)面分解的性质，设计置乱算法，并在置乱与扩散之间增加中间结果分存环节，其过程为：

第六步：记待加密的明文图像为i＝(ii,j)m×n,其中m,n分别为图像的高度和宽度；按照(4)式对像素ii,j进行bit位分解：

其中，为按照(5)式得到的二进制数，

这里mod表示取模运算，代表像素ii,j的最高位，代表最低位；令矩阵p＝(pi,j,k)m×n×8的分量为其中i＝1,2,...,m,j＝1,2,...,n,l＝1,2,...,8，定义p的m行n列二维子矩阵，p^l为：

p^l:＝(pi,j,l)m×n(6)

则8个二维二进制矩阵p^l构成明文图像矩阵i的位面分解；其中，p⁸为像素最高位对应的位面，而p¹为像素最低位对应的位面；

从伪随机二进制序列b中截取4个长度为8m的子序列，并分别将它们转化为0到255之间的整数序列s1,x,s2,x,s3,x,s4,x，其中每8个二进制数转化为一个整数，序列的长度分别为m，接着，类似地，再从b中截取4个长度为8n的子序列，并分别将它们转化为整数序列s1,y,s2,y,s3,y,s4,y，序列的长度分别为n，

分别对p⁸，p⁷和p⁶进行行列循环移位，行列循环移位是指从左至右，从上至下移位，其中，p⁸行列的移位步长分别为s1,x,s1,y，p⁷行列移位步长为s2,x,s2,y，p⁶行列移位步长为s3,x,s3,y，而p⁵,p⁴,p³,p²,p¹对应的行列移位步长都为s4,x,s4,y，即把低5位的位面作为一个整体进行行列移位操作；移位后的位面记为

从二进制序列b中截取另一长度为m·n·8的子序列，并将其重塑为4个规模为m×n×8的三维二进制矩阵d1,d2,d3,d4，根据(6)式分别定义对应的bit面它们按照(7)式形成的二维十进制矩阵被称为载体矩阵；

分别利用位面p⁸,p⁷,p⁶替换d1,d2,d3相对应的位面得到更新的三维二进制矩阵此外利用p^q,q＝1,2,...,5替换d4相应的位面得到通过位面替换，明文图像i的信息就被分存到d1,d2,d3,d4对应的4个载体矩阵中；由于p⁸,p⁷,p⁶所占的信息量比较大，分别各自使用一个载体矩阵，而p^q,q＝1,2,...,5所占的信息量较少，因此整体使用一个载体矩阵；

对执行(8)式的按位异或运算，得到新的三维二进制矩阵c，

其中，表示按位异或运算；将c按照(7)式转化为二维十进制矩阵，得到初步密文图像e。

优选的，对密文图像e的像素值进行正反双向扩散；继续从二进制序列b中截取一个长度为m·n·8的子序列，并将其进一步转化为0到255间的二维十进制矩阵f，其被称为扩散矩阵；

记正反扩散后的图像分别为g,k,先利f对e按照(9)进行正向扩散，

gi,j＝αgi,j-1+βfi,j+ei,j,gi,0＝gi-1,n(9)

其中i＝1,2,...,m,j＝1,2,...,n，参数α为新增的扩大因子，有利于增加明文变化对密文的影响，g0,n为给定的初值；反向扩散方法如下：

ki,j＝αki,j+1+βfi,j+gi,j,ki,n+1＝ki+1,0(10)

其中i＝m,m-1,...,1,j＝n,n-1,...,1,km+1,0为给定的初值；经过正反双向扩散后，k即为最终的密文图像。

本发明提出了基于四维陈氏超混沌系统与k-means聚类的图像加密方法，旨在进一步提升数字图像加密安全，同时兼顾算法的执行效率。与现有技术相比，本发明技术方案的有益效果如下：

(1)采用四维陈氏超混沌系统产生混沌序列，并利用k-means聚类算法对混沌序列进行0、1化处理，得到性能良好的伪随机二进制序列，并通过了usnist统计测试。伪随机二进制序列是加密算法的基石，具有良好伪随机性的序列从基础上保障了图像加密安全。

(2)在bit级最小粒度对图像进行置乱，并将图像按bit位进行分解，得到8个位面，其中高三位所包含的信息量高达87.84％，而低五位所占的信息量只有12.16％。根据此性质，将其中高3位对应的3个位面分别独立作为一个操作单元，而低5位对应的5个位面整体作为一个操作单元。因此，可以有效地提升算法执行效率。

(3)在传统加密方案的置乱和扩散环节中间，增加分存环节，即把置乱后的图像巧妙地嵌入四个载体矩阵，实现加密中间结果的分存。该环节进一步提升了加密安全。

(4)在图像像素扩散阶段，改进了传统的双线性扩散方案，在线性扩散递推式中添加扩大因子，以增加明文变化对密文的影响，提升加密系统应对差分分析攻击的抵御能力。

附图说明

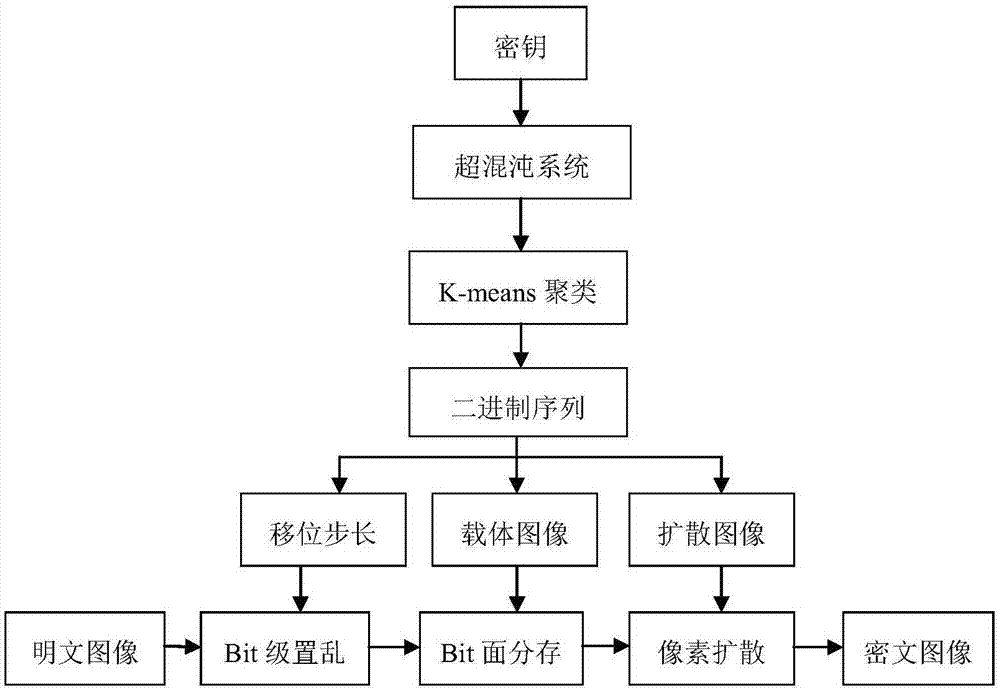
图1为本发明所提出的加密方法执行流程图。

图2为秘钥敏感性测试图；

(a)为明文lena图像；(b)为密文，加密秘钥为(18)；(c)为利用秘钥(18)解密图像；(d)为利用扰动后秘钥解密图像。

图3为明文和密文图像分别在水平、垂直和对角线方向上的相关性示意图；

(a)为明文图像水平方向相关性；(b)为密文图像水平方向相关性；(c)为明文图像垂直方向相关性；(d)为密文图像垂直方向相关性；(e)为明文图像对角线方向相关性；(f)为密文图像对角线方向相关性。

具体实施方式

附图仅用于示例性说明，不能理解为对本专利的限制；为了更好说明本实施例，附图某些部件会有省略、放大或缩小，并不代表实际产品的尺寸；

对于本领域技术人员来说，附图中某些公知结构及其说明可能省略是可以理解的。下面结合附图和实施例对本发明的技术方案做进一步的说明。

一种基于四维陈氏超混沌系统与k-means聚类的图像加密方法，以进一步提升基于混沌系统的数字图像加密安全同时兼顾加密效率，为数字图像信息安全技术领域提供重要的应用基础。

一种基于四维陈氏超混沌系统与k-means聚类的图像加密方法，具体为：

已知四维超混沌陈氏系统为：

其中，x,y,z,w为关于时间t的未知量，dx/dt,dy/dt,dz/dt,dw/dt为未知量关于时间t的导数，a,b,c,d,r为为控制参数。当参数a＝35,b＝3,c＝12,d＝7,r＝0.6时，系统(1)进入混沌状态。给定初值x＝0.1,y＝-0.1,z＝0.1,w＝-0.1,时间δt＝0.001,利用runge-kutta算法求解方程(1)得，

分别舍弃最初的一部分值，得到四个长度皆为l的实值混沌序列x＝{x1,x2,...,xl},y＝{y1,y2,...,yl},z＝{z1,z2,...,zl},w＝{w1,w2,...,wl}.

记序列x＝{x1,x2,...,xl}的最小值和最大值分别为xmin,xmax，把区间[xmin,xmax]等分成t个子区间，则t-1个等分点为i＝1,2,...,t-1.令下面利用k-means算法对序列x进行聚类处理，形成t个类，并设置t个类的初使类中心为i＝1,2,...,t.经过k-means算法处理后得到的t个类记为si,相应的类中心分别为νi,i＝1,2,...,t.

把每个类中的元素减去对应的类中心后，得到集合即i＝1,2,...,t.接着利用符号函数(2)对集合进行0、1化处理后得到二进制集合即

最后合并集合得到伪随机二进制序列

类似地，对混沌序列y＝{y1,y2,...,yl},z＝{z1,z2,...,zl},w＝{w1,w2,...,wl}进行同样的处理，分别得到二进制序列

利用x',y',z',w',根据(3)式，得到最终的伪随机二进制序列b＝{b1,b2,b3,b4,...,b4l-1,b4l}。

记待加密的明文图像为i＝(ii,j)m×n,其中m,n分别为图像的高度和宽度。按照(4)式对像素ii,j进行bit位分解

其中，为按照(5)式得到的二进制数，

这里mod表示取模运算，代表像素ii,j的最高位，代表最低位。令矩阵p＝(pi,j,k)m×n×8的分量为其中，i＝1,2,...,m,j＝1,2,...,n,l＝1,2,...,8.定义p的m行n列二维子矩阵p^l(l＝1,2,...,8)为

p^l:＝(pi,j,l)m×n,(6)

则8个二维二进制矩阵p^l(l＝1,2,...,8)构成明文图像矩阵i的位面分解。其中，p⁸为像素最高位对应的位面，而p¹为像素最低位对应的位面。

从二进制序列b中截取4个长度为8m的子序列，并分别将它们转化为0到255之间的整数序列s1,x,s2,x,s3,x,s4,x,其中每8个二进制数转化为一个整数，序列的长度分别为m.接着，类似地，再从b中截取4个长度为8n的子序列，并分别将它们转化为整数序列s1,y,s2,y,s3,y,s4,y,序列的长度分别为n.

分别对p⁸，p⁷和p⁶进行行列循环移位(从左至右，从上至下)，其中，p⁸行列的移位步长分别为s1,x,s1,y，p⁷行列移位步长为s2,x,s2,y，p⁶行列移位步长为s3,x,s3,y,而p⁵,p⁴,p³,p²,p¹对应的行列移位步长都为s4,x,s4,y,即把低5位的位面作为一个整体进行行列移位操作。移位后的位面记为

从二进制序列b中截取另一长度为m·n·8的子序列，并将其重塑为4个规模为m×n×8的三维二进制矩阵d1,d2,d3,d4.根据(6)式分别定义对应的bit面它们按照(7)式形成的二维十进制(0到255)矩阵被称为载体矩阵。

分别利用位面p⁸,p⁷,p⁶替换d1,d2,d3相对应的位面得到更新的三维二进制矩阵此外利用p^q,q＝1,2,...,5替换d4相应的位面得到通过位面替换，明文图像i的信息就被分存到d1,d2,d3,d4对应的4个载体矩阵中。由于p⁸,p⁷,p⁶所占的信息量比较大，分别各自使用一个载体矩阵，而p^q,q＝1,2,...,5所占的信息量较少，因此整体使用一个载体矩阵。

对执行(8)式的按位异或运算，得到新的三维二进制矩阵c，

其中，表示按位异或运算。将c按照(7)式转化为二维十进制矩阵，得到初步密文图像e.

为进一步提高安全性，对密文图像e的像素值进行正反双向扩散。继续从二进制序列b中截取一个长度为m·n·8的子序列，并将其进一步转化为0到255间的二维十进制矩阵f，其被称为扩散矩阵。记正反扩散后的图像分别为g,k,先利f对e按照(9)进行正向扩散，

gi,j＝αgi,j-1+βfi,j+ei,j,gi,0＝gi-1,n,(9)

其中i＝1,2,...,m,j＝1,2,...,n,参数α为新增的扩大因子，有利于增加明文变化对密文的影响，g0,n为给定的初值。反向扩散方法如下

ki,j＝αki,j+1+βfi,j+gi,j,ki,n+1＝ki+1,0,(10)

其中i＝m,m-1,...,1,j＝n,n-1,...,1,km+1,0为给定的初值。经过正反双向扩散后，k即为最终的密文图像。

其算法的执行的流程如图1所示。

本发明采用高维连续超混沌系统——四维陈氏系统来生成混沌序列，保障算法具有更大的密钥空间，并通过k-means聚类算法对陈氏系统产生的混沌序列进行0,1化处理，得到伪随机性能良好的二值序列(通过usnist统计测试)。其次，根据明文图像的位(bit)面分解的性质，设计高效的置乱算法，并在置乱与扩散之间增加中间结果分存环节，提升加密安全。最后，改进传统的线性扩散函数，利用伪随机二进制序列产生的扩散矩阵，对初步密文像素执行线性双向扩散，进一步提升系统抵御差分分析攻击的性能。

实验例

(1)usnist统计测试。利用通用标准usnist统计测试组对伪随机二进制序列b＝{b1,b2,b3,...,b4l-1,b4l}进行随机性测试。令序列长度l＝1000000，显著水平α＝0.01，表1列出了统计测试结果。可以看出，序列b很好地通过了所有的统计测试，表明其具有良好的伪随机性能。

表1二进制序列b的nist统计测试结果

(2)秘钥敏感性实验。设置秘钥为x0＝-0.1,y0＝0.1,z0＝-0.1,w0＝0.1，对明文图像lena(图2a)进行加密，得到密文图像(图2b)。接着再分别用两组秘钥对密文图像进行解密。其中，第一组为原秘钥，而第二组为对原秘钥中的x0执行一个10^-14级的微小扰动，即x0＝-0.1+10¹⁴.图2a和图2b显示了lena图像分别用第一、第二组密钥进行加、解密后的图像。可见，即使密钥相差10^-14也无法对密文图像进行正确解密。敏感性测试显示,算法对秘钥高度敏感，该测试也同时表明敏感性精度至少为10^-14.结合秘钥参数，本文的秘钥空间高达10^-140,可有效应对穷举暴力攻击。

(3)相关性分析实验。分别从明文图像和密文图像中随机选择2500对相邻的像素，然后计算相邻像素序列的相关系数。表2给出了明文和密文图像在三个方向(水平、垂直和对角线)上的相关系数。可见，相对于明文图像，密文图像的像素相关性得到了有效的降低，最高降幅达99％。图3对明文和密文图像的像素相关性进行了可视化显示。

表2明文和密文图像在三个方向的相关系数

(4)差分分析实验。差分攻击是一种常用的选择明文攻击方法，其通过分析特定明文差分对相应密文差分的影响来获得密钥。攻击者对明文图像进行微小的改动，然后对比加密前后图像之间的差别，从中寻找相关性，从而对加密方案进行破解。如果明文图像的微小改动(即使是1bit)，都能使加密后的密文图像有一半以上的像素发生改变，那么差分攻击将失效。因此，抵御差分攻击要求加密算法对明文高度敏感。这种明文敏感性通过两个指标来度量，一个是像素数改变率(numberofpixelschangerate,npcr)，另一个是归一化像素值平均改变强度(unifiedaveragechangingintensity,uaci).npcr度量的是密文像素的变化率，其越接近理想期望值99.61％，加密算法对明文变化越敏感，抵抗明文攻击的能力越强。uaci度量的是密文像素的平均变化强度，其越接近理想期望值33.46％，加密系统能越有效地抵抗各种攻击。表3给出了lena明文图像不同位置像素值变化1bit时密文图像对应的npcr和uaci，可以看出，本发明算法密文图像的npcr和uaci均非常接近于理想值。

表3密文图像的npcr和uaci计算结果.

显然，本发明的上述实施例仅仅是为清楚地说明本发明所作的举例，而并非是对本发明的实施方式的限定。对于所属领域的普通技术人员来说，在上述说明的基础上还可以做出其它不同形式的变化或变动。这里无需也无法对所有的实施方式予以穷举。凡在本发明的精神和原则之内所作的任何修改、等同替换和改进等，均应包含在本发明权利要求的保护范围之内。