通过耦合的图像相关性与机械建模来识别机械性能的计算机实现方法与流程

本发明的一般领域是材料和结构科学领域，更确切地说是材料和结构在经受各种机械应力时的性能的知识领域。

主要的工业应用与材料的强度有关。然而，还存在诸如无损检测、某些生物学应用或医用弹性成像之类的其他应用领域。

一般地，测量是借助于包括成像设备的机械测试系统进行的。这些设备主要是在可见光波长或接近可见光波长下工作的视频摄像头或静态摄像头，或是诸如扫描电子显微镜或原子力显微镜之类的微观分析系统。断层扫描装置也可用于分析材料样品的整个体积。这种装置有各种类型。将非穷尽地提及x射线断层扫描装置、磁共振断层扫描装置或“mri”和光学相干断层扫描装置。

这些成像设备的一般工作原理如下。例如，在应用确定的机械或热负载条件之前和期间，拍摄一定数量的表示样品的图像。这些图像可以是二维的、立体的或视频的，或甚至是体积图像。当然，如果期望识别具有物理尺寸的机械性能，那么对样品尺度的了解是必不可少的。

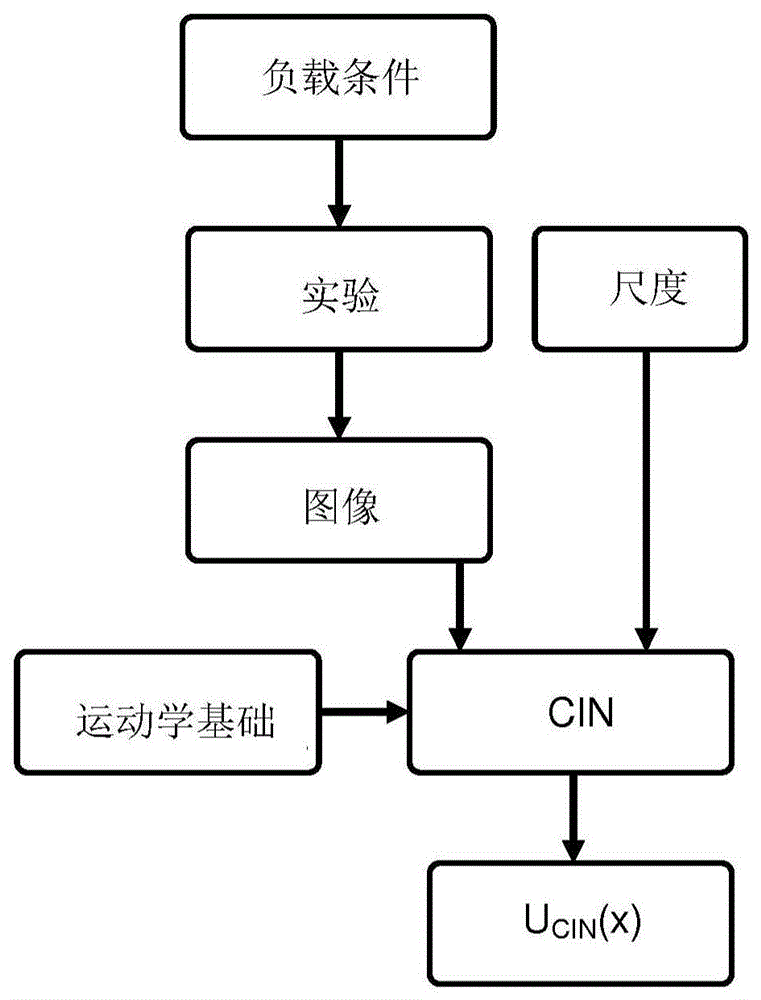
存在能够使用获得的图像来表征负载效果的各种方式。这些图像可以借助于数字图像相关性(cin)来使用，这一方法也被缩写为“dic”。将特别参考出版物“imagecorrelationforshape,motionanddeformationmeasurements:basicconcepts,theoryandapplications”，masutton，jjorteu，hschreier，springer(2009)。该方法包括在代表性运动学基础上分解样品的运动。这种基础可以是基于样品的几何网格的“有限元”类型的描述。将有负载情况下获得的多个图像与无负载情况下获得的那个或那些图像进行对比的分析使得可以测量应力情况下的样品的位移场ucin(x)，x表示样本点的坐标。图1示出了数字图像相关性方法表征的该一般原理。

同样的机械实验可以借助于有限元方法或借助于其他技术进行数值建模，以计算随后用ucal(x)表示的位移场。

建模需要：

-样品的几何形状的知识；

-包括时间的负载条件的知识，；

-诸如区域边缘的位移或力的测量值之类的边界条件的知识，；

-样品或组成样品的各相的机械行为的规律的知识；

-针对多相介质的各相的精确位置的知识。

这些不同的元素可以经由统称为{pi}的参数集以数学方式描述，i是从1变化到n的索引，n是所讨论的参数数量。图2示出了通过建模表征的该一般原理。

当然，只有当位移场ucal(x)与位移场ucin(x)相同或非常接近时，建模才能真实地反映观测值。因此，参数{pi}的优化是借助于迭代循环来实现的，在迭代循环中修改该参数，直到两个位移场彼此对应到最佳可能的程度为止。图3示出了测量、建模和优化的整个过程，使得能够确定正确的参数。

这种方法有一些缺点。具体地说，图像总是有噪声的，并且dic对这种噪声的或多或少的敏感程度取决于运动学基础的选择。在所研究区域的边缘处，这种影响尤其明显。建模的主要缺点是位移场对于某些参数的敏感性很低，使得这些参数难以确定。甚至可能在所有参数{pi}之间存在污染影响。最后，尽管存在测量缺陷，但在整个识别过程中，该位移场是不可更改的。

为了优化该方法，已经提出了各种方法。因此，名称为“elastographyimagingmodalitiesforcharacterisingpropertiesoftissue”的美国专利us7257244描述了在弹性成像的限定背景下，在图像的相关性与所讨论样品的弹性性能的建模之间进行耦合直到获得图像之间的最佳重合的迭代方法。在该方法中，假定边界条件已知，并且在迭代期间不重新考虑边界条件。

j.réthoré在int.j.num.meth.eng.84:631-660(2010)中发表的名称为“afullyintegratednoiserobuststrategyfortheidentificationofconstitutivelawsfromdigitalimages”的出版物中提出了另一种方法。该方法通过引入要被最小化的泛函来关联识别与dic，所述泛函通过强制实施两个位移场的识别来关联两个目标。识别部分通过使与平衡的偏差最小化来进行，所述与平衡的偏差是基于应用于位移的二阶微分算子的二次泛函。因此，它的最小化涉及关于位移u的四阶微分算子。

所描述的图像相关性是基于位移场的“有限元”类型离散化的全局方法。对于同一个位移场，一旦校正了当前位移场，参考图像与畸变图像之间的图像二次差以及与平衡的偏差最小化使得可以在通过dic获得的测量值和识别结果之间找到折衷点，并且关于目标本构参数{p}对该折衷点进行优化。根据图像相关性直接且唯一地产生所传递的力不为零的边界条件。该方法经由图像的重合提供了对弹性且非线性的本构规律的识别。然而，应强调的是，边缘位移的测量受到噪声的严重影响，并且使用基于位移u的二阶导数的二次泛函(通过最小化四阶微分算子产生)导致对噪声的敏感度大大增加。用这种方法处理的示例清楚地证明在施加运动学的边缘附近的误差大大增加了。在比参考文献中使用的条件更为不利的情况下，这些边界条件甚至可能妨碍机械性能的正确确定。因此，可以观察到，即使所提议的dic/识别耦合解决了上述一些缺点，但仍存在其他弱点，可能会限制定量识别能力。

更具体地，本发明的一个主题是一种识别经受机械应力的对象的、被称为“目标参数”的至少一个机械参数的计算机实现的方法，其特征在于，所述方法包括以下步骤：

-步骤1：通过成像装置获取应用所述机械应力之前和期间拍摄的所述对象的至少两个图像，并且测量所述对象的尺度因子；

-步骤2：计算第一泛函tcin(ucin)，所述第一泛函tcin(ucin)对应于数字图像的相关性，所述数字图像的相关性取决于使用第一运动学基础表示的所述位移场ucin，所述位移场ucin是在有负载和无负载的情况下、在所述对象的所述图像之间的应力下、在所述对象的任意点处进行测量的；

-步骤3：计算所述对象的任意点处的计算位移场ucal；

-步骤4：基于所述计算位移场ucal计算第二泛函tcal(ucal,{p},{q})，所述计算位移场ucal是使用第二运动学基础表示的，所述第二泛函对应于所述应力的机械模型的变分公式，所述变分公式取决于所述对象的所述几何形状、所施加的力、边界条件、至少所述目标参数{p}和预定机械参数{q}；

-步骤5：计算二次范数形式的第三泛函tpar(ucin,ucal)，所述第三泛函tpar(ucin,ucal)等于ucin与ucal之差；

-步骤6：将总泛函ttot(ucin,ucal,{p},{q})关于ucin、ucal和{p}最小化，所述总泛函ttot(ucin,ucal,{p},{q})至少包括以下项：

ttot(ucin,ucal,{p},{q})＝αtcin(ucin)+βtcal(ucal,{p},{q})+γtpar(ucin,ucal)

-α、β和γ是三个非零权重系数，所述权重系数(α,β,γ)是根据与所述泛函中涉及的各种量相关联的不确定度和/或根据与泛函ttot最小化相切的问题的条件数进行调整的。

有利的是，当对象的行为经受与时间有关的应力时，第二泛函tcal(ucal,{p},{q})取决于所确定的时间。

有利的是，该方法的步骤1包括力、时间或温度的附加测量值fmes，该方法的步骤3包括与附加测量值相对应的评估值fcal，在步骤4之后是步骤4bis，步骤4bis是计算第四泛函tfor(fcal,fmes)，第四泛函tfor(fcal,fmes)与这些量之间的二次偏差成比例，并且步骤5的总泛函ttot(ucin,ucal,{p},{q})等于：

ttot(ucin,ucal,{p},{q})＝αtcin(ucin)+βtcal(ucal,{p},{q})+γtpar(ucin,ucal)+χtfor(fcal({p},{q}),fmes)

χ是第四权重系数，权重系数χ是根据与泛函中涉及的各种量相关联的不确定度和/或根据与泛函ttot的最小化相切的问题的条件数来调整的。

有利的是，总泛函ttot的最小化是通过迭代方法实现的，这可能需要或不需要计算ttot的梯度。

有利的是，第一运动学基础与第二运动学基础相同。

有利的是，测量不确定度是由具有收敛性的泛函ttot的海塞函数通过可用的采集噪声的测量来估计的。

有利的是，第一运动学基础或第二运动学基础是在有限元网格上产生的。

本发明的另一主题是根据上述方法的适于识别至少一个机械参数的计算机设备。

本发明的另一主题是具有用于执行根据上述方法的方法的程序的计算机可读介质。

通过阅读以下不作限制的描述并且通过附图，本发明将得到更好的理解，并且其他优点将变得显而易见，其中：

已经描述的图1示出了使用称为cin(dic)的数字图像相关性方法进行监测来表示样本中的应力的各个步骤；

已经描述的图2示出了通过建模方法表示样本中应力的各个步骤；

已经描述的图3示出了通过根据现有技术的迭代方法优化目标参数{p}(诸如，机械性能、几何结构或边界条件)的各个步骤；

图4示出了通过根据本发明的迭代全局方法优化目标参数的各个步骤。

作为示例，图4示出了根据本发明的迭代全局方法优化目标参数的各个步骤。如果将根据本发明的方法与根据图3的现有技术的方法进行比较，则这两种方法之间的主要变化是运动学计算的位置，特别是关于边界条件的位置。在根据本发明的方法中，建模也介入到这些运动学值中，因此这些运动学值不再是常数，而是构成优化回路的一部分。

根据本发明的用于识别经受已知机械应力的试件或零件的本构材料的、被称为“目标参数”的至少一个机械参数的计算机实现的方法包括下述步骤。

第一步骤包括通过成像装置获取应用机械应力之前、期间和(对于某些应用)在施加机械应力之后拍摄的对象的数字图像，并且测量对象的尺度因子。事实上，如果想要确定具有物理尺寸的机械性能，那么对样品尺度的了解是必不可少的。

成像装置可以是单独使用或组合使用的、使得可以获得对象的至少一个图像的任何设备。通过所述装置获得的图像可以是在本领域技术人员熟知的各种波长范围内获得的光学图像。

其次，基于使用所选择的方法获得的图像来计算第一泛函tcin。该第一泛函对应于基于位移场ucin的数字图像的相关性，所述位移场ucin是使用(例如，有限元网格上的)第一相关运动学基础来表示的。

传统上，该第一泛函是研究区域上的参考图像与位移场的一个或多个校正失真图像之间的平方差的和，但是可以选择诸如互相关或信息的联合熵之类的其他准则。

该方法的第一步骤可能包括诸如力、时间或温度测量值之类的附加测量值fmes。

第三步骤包括计算使用第二运动学基础表示的计算位移场ucal，该第二泛函对应于应力的机械模型的变分公式，所述变分公式取决于对象的几何形状、所施加的力、边界条件、至少目标参数{p}和预定机械参数{q}。

实际上，同样的机械实验可以通过有限元方法或者通过其他技术来进行数值模拟，以计算随后用ucal(x)表示的位移场。

第四步骤包括计算第二泛函tcal(ucal,{p},{q})，所述第二泛函tcal(ucal,{p},{q})取决于一种或更多种材料的机械行为、零件的几何结构、可能包括所施加的力和以目标{p}或预定{q}参数的形式聚集在一起的一个或多个所讨论时间的边界条件，以及计算目标参数的标称值集合。该方法的第四步骤可以包括对与附加测量值fmes相对应的力、时间或温度(如果它们可用)的评估值fcal，从而可以制定与最后两个量的平方差成比例的附加泛函tfor(fcal,fmes)，该附加泛函tfor(fcal,fmes)可能由测量值的方差的倒数进行加权。

第五步骤，以ucin和ucal之间的差的二次范数形式引入第三泛函tpar(ucal,ucin)。这两个位移场与在目标参数被很好地识别且预定参数合适的情况下测量并计算的其他物理量以及所使用的模型合并在一起。

因此，所建议的识别原理是在最终步骤中，对这三个或四个泛函的权重和ttot关于两个位移场ucal和ucin以及目标参数{p}进行最小化：

ttot(ucin,ucal,{p},{q})＝αtcin(ucin)+βtcal(ucalv,{p},{q})+γtpar(ucin,ucal)+χtfor(fcal({p},{q}),fmes)

在该方法不包括附加测量值的情况下，该泛函ttot被简化为前三项。

应注意的是，如果应力范围、几何结构甚至图像的定义不合适，则问题可能仍然不适定的(ill-posed)。在这种情况下，并不是所有的目标参数都可以测量。对应于已识别参数与预期参数之间偏差的惩罚的tikhonov正则化可能需要对问题进行数值求解。然后，应使用所获得的解自身的不确定度来判断该解，例如，通过考虑预先表征的测量噪声对最小化ttot的影响而不考虑tikhonov正则化来判断。

权重系数(α,β,γ,χ)使得能够根据与泛函中所涉及的量相关联的不确定度和/或根据与泛函ttot最小化相切的问题的条件数来赋予各个项更大或更小的重要性。应当注意，任意选择的权重的任一者都可以设定为1。

如果不能直接获得机械模型的变分表达式，应注意的是，泛函tpar关于ucal的最小化可以例如在有限元代码中由线性弹性连接简单地表示，该线性弹性连接在各个节点处产生与ucal与ucin之间的偏差成比例的节点力。因此，对于使用当前专业计算机代码执行的有限元建模(其能够包括任意复杂的本构关系)，所提出的ttot公式在其关于ucal的最小化中只需要在网格的各个节点处引入附加线弹性连接。所得到的解正是在ucin、{p}和{q}固定的情况下使总泛函最小化的解。通过关于不同的未知数子集来交替进行最小化步骤，使得如果该问题是适定的，则可能达到目标最小化。

例如，可以经由连续线性化和校正，借助于牛顿-拉斐逊方法来执行泛函ttot的最小化。

有利的是，具有收敛性的泛函ttot的海赛函数(hessian)使得如果例如在执行机械实验之前经由无应力情况下的重复采集获得了对采集噪声的测量值，则可以估计测量不确定度。特别地，可以理解，问题的适定性对应于严格正的特征值，并且在这种情况下，条件数对应于海赛函数的谱半径。否则，可以提出tikhonov正则化。

有利的是，这些元素也使模型有效或无效。具体地：

-位移场ucin使得能够估计图像相关性的剩余场，即，ucin位移场的畸变和校正图像与参考图像之间的差；

-建模使得可以验证本构规律和平衡条件是否满足；

-可获得的任何附加测量值与从建模中得到的那些值进行比较；

-将两个位移场(一个位移场接近测量值ucin，另一个位移场接近模型ucal)组合在衡量这两种方法的一致性的同一个泛函中。

因此，所使用的各个泛函都提供了自己的验证。相反地，残差太大，无法与采集噪声信号模型或测量误差兼容，并且提供了关于如何丰富解释性模型或识别非预期测量伪影的指示。

有利的是，泛函的各个项的耦合使得能够补偿这个泛函或那个泛函的不适定性或病态性(ill-conditionedcharacter)。例如，低对比度或照明不足的区域可能不允许仅使用泛函tcin来测量ucin。然后，泛函tpar可以通过计算来补偿信息的缺乏。

对称地，当本构规律或几何非线性导致机械问题解的稳定性或唯一性丧失时，耦合泛函tpar随即使得可以恢复问题的适定性，并且经由模型跟踪同一分支。

在收敛的情况下，针对位移场ucin、不同计算出的位移场ucal、模型fcal的力、时间或温度或其他物理量的值、以及识别对象的目标参数{p}的估计，总泛函达到其最小值。这些参数可能是与一个或更多个相有关的材料的参数，或是对象的几何结构或其他量(例如边界条件)。

该方法由计算机实现，因此可以根据上述方法使计算机设备适于识别至少一个机械参数。

因此，根据本发明的方法基本上可以通过使用当前计算工具完全可以实现的数值计算装置来实现，但是在实践中可以分析更广泛的材料，或者使用更便宜的硬件(尤其是与给定最终结果的采集硬件的质量有关)。