饱和多孔介质大变形分析的CCPDI-IMPM方法与流程

本发明属于计算力学技术领域，具体涉及一种饱和多孔介质大变形分析的ccpdi-impm方法。

背景技术：

饱和多孔介质是一种自然界中广泛存在的多相多孔材料，其由可变形的固体骨架及充满其间的孔隙流体共同组成。近几十年来，由于饱和多孔介质具有复杂的力学性质而被科研人员高度关注，并在岩土工程、生物工程等诸多领域被广泛应用。通过对其进行数值模拟可以得到可靠的仿真结果进而对实际工程应用中多孔结构的功能性和安全性进行有效评估，从而对相关地质灾害预防、安全高效生产及人体健康防护等众多方面均产生了重要意义。例如，岩土工程中常应用的边坡、堤坝的稳定性分析和石油及页岩气开采过程中涉及的水力压裂技术；生物工程中有关动物体内生物软组织的动力响应及非线性行为的数值分析等。因此，在现今计算机技术快速发展的时代，发展高效的数值计算方法并结合计算机超高的计算能力对结构在复杂工况条件下进行深度数值仿真分析已成为前沿科技发展的主流趋势。对于饱和多孔介质的数值模拟相关理论研究最早可追溯到terzaghi固结理论，随后biot将其理论拓展至三维固结分析，并建立了考虑饱和多孔介质内流-固相互作用的动力控制方程，即biot理论。之后，truesdell等人提出混合物理论，bowen等人基于此理论发展了土力学中耦合系统方程。为了进一步研究变形土体的强非线性行为，zienkiewicz和prevost提出了广义增量方程为分析饱和土的材料非线性及大变形行为提供了求解方法。而后，prevost首次采用有限单元法(fem)对饱和多孔介质的非线性行为进行了数值模拟，为之后饱和多孔介质理论的快速发展奠定了基础。1984年，zienkiewicz从土壤整体平衡方程和流体运动方程出发，基于terzaghi有效应力理论建立了饱和土的广义biot理论模型，并导出了适用于高速运动过程分析的饱和多孔介质固以相位移和液相位移为未知变量的u-u控制方程，及适用于中、低速运动过程的动力和固结过程分析的以固相位移和孔隙流体压强为未知变量的u-p控制方程。之后，一系列基于fem方法的饱和多孔介质理论模型被提出，如：两相流体模型，热-水-力模型，全耦合动力模型等。

随着理论研究不断深入，运用fem分析大变形、冲击及侵彻等问题时存在诸多困难，由于其自身的强网格依赖性致使结构变形较大时局部网格会发生严重畸变，因而需要网格重构，但这不仅增大了计算量，而且严重影响计算精度。由此，无网格法的提出成功解决了上述难题，而物质点法(mpm)作为一种最具有代表性的无网格法，自1994年被sulsky提出至今已得到快速发展。由于mpm最初被提出是基于显式时间积分方法，故其被广泛用于求解动力问题。研究发现运用显式物质点法(empm)分析准静态问题时存在计算量大、计算精度低，以及求解一些耦合场问题时存在边界处理相较复杂等缺陷，而guilkey提出的基于隐式时间积分格式的物质点法(impm)很好地克服了上述empm的缺陷，且兼并传统物质点法求解大变形问题的优势。因此，本工作将采用隐式物质点法(impm)并结合对流粒子域插值技术(cpdi)发展一种耦合对流粒子域插值隐式物质点法(ccpdi-impm)对饱和多孔介质大变形固结/动力过程展开相关研究。

技术实现要素：

本发明要解决的技术问题：本发明采用基于混合物理论的饱和多孔介质连续体模型，创新性的提出了一种饱和多孔介质大变形固结/动力分析的耦合对流粒子域插值隐式物质点方法(ccpdi-impm)，其目的在于解决现有技术存在的以下问题：克服基于传统fem方法模拟饱和多孔介质大变形时发生网格畸变造成严重数值误差的缺陷；克服基于empm方法模拟饱和多孔介质固结/动力过程时施加流体压力边界条件过程复杂的不足，并且最重要的是发展一种新的耦合物质点算法克服应用传统empm求解固结问题出现计算量大、计算精度低等问题。

本发明的技术方案：

饱和多孔介质大变形分析的ccpdi-impm方法，

基于广义biot理论的u-p形式控制方程，以及对流粒子域插值技术(cpdi)，提供了一种饱和多孔介质大变形分析的ccpdi-impm方法，该方法主要包括饱和多孔介质大变形固结过程分析及饱和多孔介质大变形动力过程分析两个部分，具体步骤如下：

(1)首先，针对饱和多孔介质大变形固结过程分析，基于等温假设，且忽略阻尼效应和不考虑重力影响情况下，其耦合系统强形式控制方程为：

式中：σ＝σ″-αpi为总应力张量，σ″为有效应力张量，p为液相孔隙压强，α为biot系数，i是二阶单位张量，b为体积力矢量，ρ为混合物密度，表示成ρ＝nρw+(1-n)ρs，n为孔隙率，ρs、ρw分别表示固相和液相的密度，为孔隙压力变化率，为固相速度矢量，kw为渗透率，表示为kw＝k/μw，k为固有渗透系数，μw为液相动力粘性，ks、kw分别表示固相和液相的体积模量；

耦合系统的初始条件、边界条件为：

初始位移、压强边界条件：在求解域ω和边界上u＝u0，p＝p0

式中：u0、u、分别为初始位移、固相位移、指定边界位移，为指定边界面力，nτ为在边界上外法线矢量，且有p0、p、分别为初始压强、液相孔隙压强、指定边界压强，为指定边界流量，nq为在边界上外法线矢量，且有

然后，对式(1)、(2)中耦合系统强形式控制方程进行空间域上离散，先采用galerkin法并考虑式(3)中耦合系统初始和边界条件，获得其弱形式控制方程为：

式中：w^s、w^w分别是位移场和孔隙压力场的任意试函数；

再通过在物质点上累加获得其空间离散方程：

式中：np表示物质点总数，nn表示活动网格节点总数，vp表示物质点p的粒子域体积，上标s、w分别表示变量与位移场和压力场相关，下标p、i分别表示变量与物质点和背景网格节点相关，φi、分别表示背景网格广义插值数值基函数及其梯度，表示可替代的背景网格数值基函数；

由于试函数是任意函数，故上式(6)、(7)整理得到如下矩阵方程：

最后，采用newmark积分和newton-raphson迭代策略对空间离散方程(8)在时域上进行离散，通过推导可得如下耦合系统对称的离散格式迭代方程和耦合系统等效刚度矩阵：

式中各变量表征如下：

固-液耦合矩阵

液-固耦合矩阵

液相压缩矩阵

液相渗流矩阵

固相切线刚度矩阵

固相外载荷

液相外载荷

上述式(15)中kmat、kgeo分别表示固相材料刚度矩阵和固相几何刚度矩阵，且各式中上标i，n+1表示n+1时间步内第i个迭代步，其中δ、θ为newmark积分参数，δt为时间增量，分别表示位移场和压力场的插值形函数，bi，l、bi，nl分别表示压力场梯度算子、线性应变-位移矩阵和非线性应变-位移矩阵，为cauchy应力矩阵，表示材料本构张量，m在处理一维、二维问题时为[110]^t，处理三维问题时为[111000]^t；

过程二：对于饱和多孔介质大变形动力过程分析，其相较固结分析过程考虑了惯性力项，基于等温假设，且忽略阻尼效应和不考虑重力影响情况下，其强形式控制方程为：

其中为固相加速度矢量；

耦合系统的初始条件、边界条件为：

由于式(18)、(19)中耦合系统强形式控制方程在空间域和时间域上离散方式与固结过程一致，故此直接给出其空间离散方程和时间离散方程的表达式，则空间离散方程为：

耦合系统对称的时间离散迭代方程和耦合系统等效刚度矩阵为：

式中固-液耦合矩阵csw、液-固耦合矩阵cws、液相压缩矩阵pww、液相渗流矩阵hww、固相刚度矩阵kt、固相外载荷液相外载荷如式(11)-(17)所示，且混合物质量矩阵m、液相质量矩阵mw表达如下：

混合物质量矩阵

液相质量矩阵

根据上述理论推导得出的饱和多孔介质固结/动力分析过程的增量迭代离散形式控制方程，并选取材料本构模型，再结合cpdi插值方法和impm数值计算方法即可实现本发明提出的饱和多孔介质大变形分析的ccpdi-impm方法，其具体实施步骤如下：

步骤一、在所研究问题求解域内建立离散物质点模型、划分euler背景网格，并定义物质点物理材料参数，且根据给定初始条件初始化域内物质点的物理属性，以及根据具体问题选择饱和多孔介质大变形数值分析过程；

步骤二、初始化euler背景网格，并在离散的物质点和网格节点间通过cpdi插值方法建立映射关系，对euler网格划分活动网格及非活动网格、活动节点及非活动节点；且通过插值函数将物质点携带的物理信息映射到背景网格节点，再由newmark积分策略初始预测网格节点运动状态；

步骤三、根据确定的饱和多孔介质大变形数值分析过程选择对应状态离散控制方程，并以物质点作为积分点完成耦合系统等效刚度矩阵的组装，并施加位移场和孔隙压力场边界条件，再通过newmark积分策略更新网格节点动量信息及利用newton-raphson迭代策略完成当前时间步内耦合系统增量迭代方程求解；

步骤四、根据后变形后的背景网格节点信息更新物质点位置及运动状态，并返回步骤二，进入下一计算时间步，直至数值计算完成。

在步骤二中，采用cpdi插值技方法需基于如下两个基本假设：粒子域为平行四边形，以及变形梯度在粒子域内近似常数；则广义插值网格奇函数及其梯度解析表达为：

式中：vp为物质点p的粒子域体积，和分别表示粒子域向量坐标，表示物质点p的粒子域角点i关于euler背景网格的插值基函数；

在步骤二、步骤三中，采用newmark积分策略更新背景网格节点动量信息，具体实施过程如下：

式中：和δt为时间增量，δ、θ为newmark积分参数，且需满足无条件稳定条件：δ≥0.5，θ≥0.25(0.5+δ)²；

在步骤三中，为了有效施加耦合系统的位移场和孔隙压力场边界条件，提出一种扩展物质点罚因子法(参见图2)用以处理物质点上施加指定位移边界和压力边界条件；假定域内有n6个活动网格节点，p^s、p^w分别为指定位移物质点和指定压力物质点，则具体实施过程为：

首先，形成以下系数矩阵和系数向量：

位移场系数矩阵

压力场系数矩阵

边界约束系数向量

式中：为1×n6的矩阵，为2×2n6的矩阵，dof为1×3的向量，分别表示物质点p^s上指定位移自由度和物质点p^w上指定压力自由度；

然后，外力载荷向量、内力载荷向量和耦合系统全局等效刚度矩阵被修正为：

外力载荷向量

内力载荷向量

耦合系统全局等效刚度矩阵

式中：δdof为背景网格自由度增量向量，分别为位移场和孔隙压力场的罚因子；同理，该扩展物质点罚因子法亦与将物质点相关变量替换为与物质点所在粒子域各角点的相关物理量，即实现耦合系统的边界条件施加在粒子域角点上；

饱和多孔介质大变形分析的ccpdi-impm方法的数值实现过程将通过如下伪代码形式展示：

step1.建立饱和多孔介质离散的物质点模型；

step2.定义euler计算网格和物质点物理参数：混合物质量mp、初始体积初始位移初始粒子域向量初始变形梯度杨氏模量ep、泊松比vp、初始有效应力初始孔隙压力初始加速度初始速度初始孔隙压力变化率总时间步数nstep、总迭代步数niter、收敛容差tol；

step3.for：h＝1，2…nstep，do

step3.1初始化背景网格：搜索活动背景网格单元及节点：活动网格节点总数nn、节点自由度总数ndofs、活动网格单元总数ncells，并将物质点和活动网格节点间进行关系匹配；

step3.2通过cpdi插值方法对每个物质点均计算插值网格奇函数及其梯度

及线性和非线性应变-位移矩阵并且初始化网格节点位移增量向量和压力增量向量

step3.3将物质点物理参数mp、映射到网格节点mi、

step3.4采用newmark积分策略初始预测th+1＝th+δt时刻网格动力信息：

step3.5施加外载荷和流量边界：

step3.6初始化耦合系统增量自由度向量：

step3.7for：k＝1，2…niter，do

step3.7.1计算等效刚度矩阵：

step3.7.2计算残差力向量：

step3.7.3施加位移场、孔隙压力场边界约束，并求解耦合系统增量迭代方程：

step3.7.4计算h+1时间步内耦合系统自由度增量向量：

step3.7.5采用newmark积分策略更新当前迭代步网格节点加速度、速度、孔隙压力变化率：

step3.7.6更新物质点变形梯度：

step3.7.7更新当前迭代步孔隙压力场插值函数梯度线性和非线性应变-位移矩阵

step3.7.8更新物质点孔隙压力梯度：

step3.7.9更新物质点体积：

step3.7.10更新变形后物质点的位置位移孔隙压力

step3.7.11收敛性判断：如果且或k≥niter，则进入step3.8；否则返回step3.7；

step3.8更新物质点的孔隙压力变化率、加速度、速度：

step3.9更新物质点的粒子域向量：

step3.10保存收敛后物质点上各物理量进入下一计算时间步：如果h≤nstep，则返回step3；否则进入step4；

step4.计算结束，保存并输出结果。

上述伪代码展示了饱和多孔介质大变形动力分析过程的详细数值实施流程，当考虑饱和多孔介质大变形固结分析时，仅需将系统惯性力项忽略，即在步骤3.4和步骤3.7.5更新网格节点动量信息时设置并且在步骤3.8中更新物质点速度时可采用背景网格节点的速度直接插值得到。

在步骤3.7.6中物质点的变形梯度采用增量形式更新，即用当前时间步内增量变形梯度乘以上一时间步收敛后的变形梯度。则当前时间步内增量变形梯度采用如下方程计算：

然后，通过上述增量变形梯度的逆矩阵乘以当前时间步初始插值形函数梯度即可更新当前变形后的插值形函数梯度：

最后即可更新每一时间步内迭代步所需的背景网格插值形函数梯度线性和非线性应变-位移矩阵式中表示当前h+1时间步内网格节点位移增量，分别表示当前h+1时间步初始物质点位置坐标和当前迭代步变形后物质点位置坐标，δij表示狄拉克函数。

本发明的有益效果：

采用本发明提供的技术方案与现有技术相比，具有如下显著效果：

(1)本发明提供的一种饱和多孔介质大变形分析的ccpdi-impm方法，通过采用对流粒子域插值技术(cpdi)克服了传统物质点方法中因物质点穿越网格边界造成数值不稳定及计算精度低的问题，并且该方法结合cpdi的网格边界光滑插值优势及impm的euler-lagrangian描述优势在处理大变形及极端变形时相较传统fem计算性能更加稳健；

(2)本发明提供的一种饱和多孔介质大变形分析的ccpdi-impm方法，通过采用隐式时间积分策略克服了传统empm受临界时间步长限制的缺陷，特别在求解准静态问题时显著提高计算效率，如饱和多孔介质大变形固结过程分析，并且采用隐式时间积分策略相较于显式积分还可提高计算精度，解决了应用基于传统empm方法求解饱和多孔介质变形问题时物质点孔隙压力对背景网格划分密度产生敏感性的问题；

(3)本发明还创新性的提供了一种扩展物质点罚因子法(参见图2)用以处理物质点上施加指定位移边界和压力边界条件，规避了应用传统empm方法模拟饱和多孔介质变形问题时需设定边界压强层用以施加压强边界条件操作复杂的问题，并且描述耦合系统边界条件更加真实准确。

附图说明

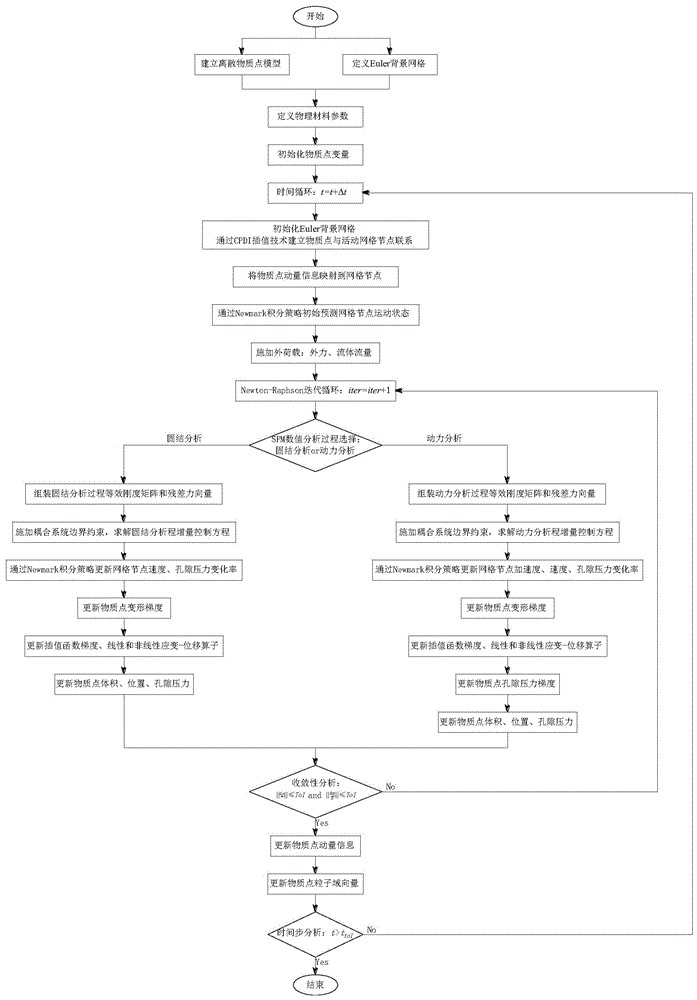
图1为本发明的一种饱和多孔介质大变形分析的ccpdi-impm方法的操作流程图；

图2为本发明的一种扩展物质点罚因子法的施加耦合系统边界示意图；

图3为本发明大变形固结过程分析实施例1二维饱和矩形土块结构及加载示意图；

图4为本发明大变形固结过程分析实施例1中a点竖向沉降位移时程曲线结果对比图(a)载荷f＝1.5×10⁶pa、(b)载荷f＝2.4×10⁶pa；

图5为本发明大变形固结过程分析实施例1中b点水平位移时程曲线结果对比图(a)载荷f＝1.5×10⁶pa、(b)载荷f＝2.4×10⁶pa；

图6为本发明大变形固结过程分析实施例1中c点孔隙压力时程曲线结果对比图(a)载荷f＝1.5×10⁶pa、(b)载荷f＝2.4×10⁶pa；

图7为本发明大变形固结过程分析实施例1由fem(a-c)及ccpdi-impm(d-f)在载荷f＝1.5×10⁶pa工况下得到的不同时刻(a)(d)55.6h、(b)(e)125h、(c)(f)166.7h结构内部孔隙压力分步云图；

图8为本发明大变形固结过程分析实施例1由ccpdi-impm在载荷f＝2.4×10⁶pa工况下得到不同时刻(a)111.1h、(b)200h、(c)250h结构发生极端大变形时内部孔隙压力分步云图；

图9为本发明大变形动力过程分析实施例2二维饱和方形土块结构及加载示意图；

图10为本发明大变形动力过程分析实施例2中a点竖向位移时程曲线结果对比图(a)载荷f＝1.5×10⁷pa、(b)载荷f＝2.4×10⁷pa；

图11为本发明大变形动力过程分析实施例2中a点孔隙压力时程曲线结果对比图(a)载荷f＝1.5×10⁷pa、(b)载荷f＝2.4×10⁷pa；

图12为本发明大变形动力过程分析实施例2由fem(a-d)及ccpdi-impm(e-h)在载荷f＝1.5×10⁷pa工况下得到的不同时刻(a)(e)0.2s、(b)(f)0.4s、(c)(g)0.6s、(d)(h)0.8s结构内部孔隙压力分步云图；

图13为本发明大变形动力过程分析实施例2由ccpdi-impm在载荷f＝2.4×10⁷pa工况下得到不同时刻(a)0.2s、(b)0.4s、(c)0.6s、(d)0.8s结构发生极端大变形时内部孔隙压力分步云图。

具体实施方式

下面结合附图和实施例对本发明的实施方式作进一步详细说明。以下实施例用于说明本发明，但不能用来限制本发明的范围。

为了使本发明的目的、技术方案和优点展示更加清晰明了，下面通过两个具体实施例结合附图3～13对本发明的优势性、准确性和有效性做进一步的详细说明。

首先，针对饱和多孔介质大变形固结/动力过程模拟，本发明示例性的选取可压缩neo-hookean材料用以描述饱和多孔介质固体骨架的大变形行为，其应变能密度函数为：

式中μ0和λ0分别表示剪切模量和第一拉梅常数，c＝f^tf为右cauchy-green张量，f为变形梯度，j＝det(f)为变形梯度的jacobi行列式，ic＝trace(c)和j²＝iiic＝det(c)分别表示右cauchy-green张量的第一和第三不变量。

定义λ＝λ0和μ＝μ0-λlnj，再通过应变能密度函数对右cauchy-green张量求一阶偏导数，则饱和多孔介质的有效cauchy应力可以表示为：

然后通过乘法链式法则使应变能密度函数对右cauchy-green张量求二阶偏导数，即可得推导出前推到当前构型的空间弹性张量：

以下两个实施例中为了便于比较，本发明的euler背景网格尺寸设置与fem的单元网格尺寸一致，并且每个网格内物质点的数量与高斯积分点的数量相同。

表1饱和多孔介质参数说明

(1)实施例一：饱和多孔介质大变形固结过程分析(附图3～8)

如图3所示，实施例一为平面应变假设条件下二维饱和矩形土块在上端中部竖直加载作用下结构变形与内部流体流动演化问题。如图3(a)所示，矩形土块结构尺寸为40m×25m，对该结构上、下边界均为非渗透边界，并且下边界固定水平和竖直方向自由度，而左、右边界均为p＝0自由渗透边界，并且均固定水平方向自由度。对于本发明提出的ccpdi-impm采用80×50个物质点的离散模型，则fem相应将模型划分40×25个有限单元。本实施例采取f＝1.5×10⁶pa和f＝2.4×10⁶pa两个工况载荷，如图3(b)所示，对于工况一f＝1.5×10⁶pa：时间增量步长δt＝200s，线性加载时间t0＝125h，总固结模拟时间t＝222.2h；对于工况二f＝2.4×10⁶pa：时间增量步长δt＝200s，线性加载时间t0＝200h，总固结模拟时间t＝355.5h。选择特征点a(20m，25m)、b(10m，15m)、c(20m，10m)并考察其上位移和孔隙压力随时间变化关系。具体饱和多孔介质材料参数如下表2所示。

表2饱和多孔介质大变形固结过程分析材料参数及变量设置

图4～图6分别展示了两种载荷工况下a点的竖直沉降位移时程曲线、b点的水平位移时程曲线、c点的孔隙压力时程曲线。对于工况载荷f＝1.5×10⁶pa的数值模拟结果如图4(a)～图6(a)所示及图7所示该工况载荷下不同时刻结构内部孔隙压力演化云图，可以看出本发明提出的ccpdi-impm方法所获得结果与传统fem结果几乎完全吻合，从而验证了本发明所提出的方法分析饱和多孔介质大变形固结过程的准确性和有效。对于工况载荷f＝2.4×10⁶pa的数值模拟结果如图4(b)～图6(b)可以观察到传统fem由于结构在极端大变形情况下发生严重的网格畸变从而导致数值计算中断，但是，本发明提出的ccpdi-impm方法对极端大变形模拟依然展现出稳健的性能，数值模拟结果良好。进而结合图8为极端大变形情况下不同时刻结构内部孔隙压力演化云图可以有效说明本发明提出的ccpdi-impm方法相较传统fem处理饱和多孔介质固结分析大变形及极端大变形时的有效性和优越性。

此外，在本算例载荷工况f＝1.5×10⁶pa的数值模拟过程中，我们还采用基于显式积分格式ccpdi-empm方法对该固结过程模拟了前10s，由于其是使用显式积分策略，故增量时间步长选取受限于courant-friedrichs-lewy条件，则设置δt＝2×10^-3s，且基于frotran语言编制的ccpdi-empm算法模拟固结过程的前10s使用cpu时间为1397s，由此可以推算模拟整个固结过程需耗时约1293天，而采用本发明的ccpdi-impm模拟整个历程仅需约7小时。因此，通过该实施例又进一步验证了本发明提出的ccpdi-impm由于采用隐式积分策略则相较ccpdi-empm处理静态及准静态问题时更加高效省时。

(2)实施例二：饱和多孔介质大变形动力过程分析(附图9～13)

如图9所示，实施例二为平面应变假设条件下二维饱和方形土块垂直加载动力问题分析。如图9(a)所示，土块结构尺寸为10m×10m，对该结构的上边界设置为p＝0自由渗透边界，左、右、下边界均为非渗透边界，并且下边界固定竖直方向自由度，左、右边界均固定水平方向自由度。对于本发明提出的ccpdi-impm和对比算法ccpdi-empm均采用40×40个物质点的离散模型，则fem相应将模型划分20×20个有限单元。本实施例采取f＝1.5×10⁷pa和f＝2.4×10⁷pa两个工况载荷，如图9(b)所示，对于两种载荷工况：线性加载时间t0＝0.1s，总模拟时间t＝1s。对于ccpdi-impm及fem设置其时间增量步长δt＝1×10^-3s，而ccpdi-empm设定时间增量步长δt＝1×10^-4s。选择特征点a(2m，8m)并考察其上位移和孔隙压力随时间变化关系。具体饱和多孔介质材料参数如下表3所示。

表3饱和多孔介质大变形动力过程分析材料参数及变量设置

图10、图11分别展示了两种载荷工况下a点的竖直位移时程曲线和孔隙压力时程曲线。对于在工况载荷f＝1.5×10⁷pa下三种数值方法所得如图10(a)、图11(a)所示a点历史曲线对比结果及图12所示采用本发明的ccpdi-impm及fem获得的不同时刻结构内部孔隙压力演化云图，可以清晰看出本发明提出的ccpdi-impm方法数值模拟获得的结果与其他两种对比方法的结果吻合良好，从而验证了本发明所提出的方法分析饱和多孔介质大变形动力过程的准确性和有效。从图10(b)～图11(b)中可以观察到传统fem在工况载荷f＝2.4×10⁶pa的饱和多孔介质极端大变形动力过程模拟中由于网格畸变先产生较大数值误差，最后导致数值计算中断。而本发明提出的ccpdi-impm方法和所采用的对比算法ccpdi-empm对极端大变形模拟依然表现出算法的稳健性，得到良好的数值模拟结果。并且结合图13为本发明的ccpdi-impm在极端大变形情况下获得不同时刻结构内部孔隙压力演化云图可以很好的说明本发明提出的ccpdi-impm方法相较传统fem处理饱和多孔介质动力分析极端大变形时的有效性和优越性。而在本实施例中ccpdi-impm采用比ccpdi-empm更大的增量时间步长得到的结果仍吻合良好，一定程度上提高了计算效率，从而说明了本发明所提出方法的采用隐式积分策略的优越性和准确性。

综上所述，通过三种不同的数值方法对上述两个典型实施例进行有效数值模拟，可以很好的说明本发明提出的一种饱和多孔介质大变形分析的ccpdi-impm方法的可行性和发展必要性，通过精确的数值结果对比阐释了本发明提出ccpdi-impm方法的有效性和准确性，且因其自身euler-lagrangian描述特性使其在饱和多孔介质极端大变形模拟中表现出比fem更稳健的计算性能。虽然本发明给出的两个实施例是对二维饱和多孔介质大变形问题进行了数值模拟，但其很容易被拓展至三维饱和多孔介质大变形问题分析。因此，本发明提出的ccpdi-impm方法是一种颇具发展潜力的高效算法。

本发明的实施例是为了示例和描述起见而给出的，而并不是无遗漏的或者将本发明限于所公开的形式。很多修改和变化对于本领域的普通技术人员而言是显而易见的。选择和描述实施例是为了更好的说明本发明的原理和实际应用，并且使本领域的普通技术人员能够理解本发明从而设计适于特定用途的带有各种修改的各种实施例。