一种融合多个特征的多尺度目标跟踪方法与流程

本发明涉及一种计算机视觉目标跟踪技术领域，具体的涉及一种融合多个特征的多尺度目标跟踪方法。

背景技术：

目标跟踪是计算机视觉中重点研究方向之一，包含了机器学习、事件检测、信号处理、视频监控、自动驾驶、统计学等相关方面知识。虽然目标跟踪这些年取得了很大进展，但由于跟踪目标存在诸如遮挡、快速运动、模糊、光照及变形等因素，相关滤波跟踪方法仍面临巨大挑战。

现有的基于多特征的目标跟踪方法的不足之处在于无法处理遮挡、变形和平面外旋转。当目标发生遮挡而导致跟踪失败时，没有目标重检测模块，本文在现有方法的跟踪器的基础上，优化了寻找输出响应最大值所对应的最佳尺度估计和目标最佳中心点位置的方法，并提出了利用图像分块重检测的思想，对分块后的图像块逐一进行相关滤波，找出最大响应值的位置，更新当前帧的目标中心点位置。此外引入模型更新策略，目标正常跟踪则正常更新模型，当目标开始遮挡时，更新缓慢甚至停止更新模型，防止产生模型的错误累积。

技术实现要素：

为了弥补先有技术的不足，本发明提供了一种从分类器训练、模型更新和自适应尺度估计三方面提出一种融合多个特征的多尺度目标跟踪方法。

为实现上述目的，设计了四个部分：分类器训练、位置估计、自适应尺度估计和模型更新。

其各个部分的方法如下：

所述分类器训练，通过建立最小化代价函数为每层神经网络训练一个位置滤波器，得到最优相关滤波器：

式(1)中，f^l是一个d维特征向量，d代表所选特征的维数,l∈{1,2,...d}。每个通道对应的滤波器为h^l，*表示卷积运算，上标l表示特征的某一维度，g表示理想高斯函数输出，l是正则化系数，λ的作用一方面是消除频谱中零频分量的影响，另一方面避免滤波器过拟合，式(1)可在频域中求解得式(2)：

其中，大写字母为对应变量的频域形式，上划线表示该变量的共轭复数。

所述位置估计用于预测目标位置，其具体工作为：

滤波器训练完成后对下一帧的目标进行位置估计，提取测试样本的hog特征和cn特征后，分别得到相应特征目标位置的空间响应：

其中表示傅里叶反变换，z表示新一帧中输入的候选样本的频域描述。采用固定权重融合策略进行hog特征和cn特征的响应图融合，响应最大值即为预测目标位置。融合公式为：

y＝(1-r)yhog+rycolor(4)

所述的尺度估计工作为：

在对目标进行尺度估计时,利用目标图像的hog特征，在预测目标位置上，利用尺度滤波器找到目标最佳尺度。目标尺度估计过程与位置滤波器预测目标位置类似，具体操作为：

假设输入样本大小为p×r，目标最佳尺度由输入样本与一维尺度滤波器进行卷积得到的尺度响应最大值确定，评估目标尺度样本的选择原则为：

式(5)中，a为步长因子；p、r分别为目标在前一帧的宽、高；s为尺度数量。

所述的滤波器更新方式：

对于跟踪任务来说目标始终处于变化之中，需对位置和尺度滤波器进行更新以适应目标外观及尺度变化。为解决图像中的每个像素点要计算d×d维的线性方程，可以对式(2)中分子和分母bt分别进行更新:

位置滤波器和尺度滤波器均按照式(6)进行更新。为了避免因遮挡、旋转、光照变化等情况影响模型更新训练，出现跟踪漂移现象，本文方法引入模型更新策略控制模型更新的快慢，目的在于减小目标模型的累积错误。设定一个阈值tr，当响应最大值y>tr时，则正常更新当前帧(第t帧)的模型即公式(6)；反之，则认为此时的目标区域存在不确定性，不予以更新。

本发明的与现有的主流相关滤波跟踪方法相比，其优点在于：

1、hog特征对目标细小形变、光照变化等有较好的适应能力，但当目标发生较大形变或遮挡时，hog特征不能适应目标变化从而丢失目标；cn特征是一种基于像素点的全局特征，能够有效处理目标形变和尺度变化问题，但是无法适应光照变化。所以利用融合hog特征和cn特征的方式，能很好地互补其缺点，使跟踪能够适应各种情况，提高目标跟踪方法的准确性和鲁棒性。

2、提出了一种基于图像分块重检测的改进方法，优化了最大响应搜索方法，同时引入模型自动更新策略能够有效处理目标遮挡问题，在光照变化、遮挡、运动模糊和旋转等复杂场景下能够实现鲁棒的目标跟踪。

附图说明

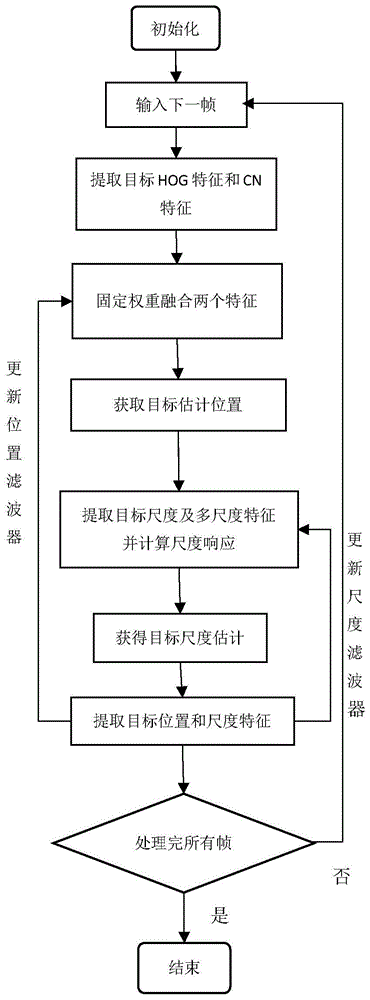
图1是本发明的方法流程图。

具体实施方式

为了对本发明的技术特征、目的和效果有更加清楚的理解，现对照附图说明本发明的具体实施方式。

图1是本发明的方法流程图：

第一步：获取目标的初始位置信息以及尺度信息。

第二步：根据第一步获取的初始信息提取目标的hog特征和cn特征。

通过建立最小化代价函数训练一个位置滤波器，得到最优相关滤波器：

式(1)中，f^l是一个d维特征向量，d代表所选特征的维数,l∈{1,2,...d}。每个通道对应的滤波器为h^l，*表示卷积运算，上标l表示特征的某一维度，g表示理想高斯函数输出，λ是正则化系数，λ的作用一方面是消除频谱中零频分量的影响，另一方面避免滤波器过拟合，式(1)可在频域中求解得式(2)：

其中，大写字母为对应变量的频域形式，上划线表示该变量的共轭复数。

第三步：根据第二步分别建立相关滤波模型，提取测试样本的hog特征和cn特征，分别得到相应特征目标位置的空间响应：

其中表示傅里叶反变换，z表示新一帧中输入的候选样本的频域描述。

采用固定权重融合策略进行hog特征和cn特征的响应图融合，响应最大值即为预测目标位置。融合公式为：

y＝(1-r)yhog+rycolor(10)

第四步：根据第三步的滤波响应，预测目标位置。响应最大值y即为预测目标位置。

第五步：根据第四步预测的目标位置信息，在此基础上对目标提取hog特征,利用尺度滤波器找到目标最佳尺度。

设输入样本大小为p×r，目标最佳尺度由输入样本与一维尺度滤波器进行卷积得到的尺度响应最大值确定，评估目标尺度样本的选择原则为：

式(5)中，a为步长因子；p、r分别为目标在前一帧的宽、高；s为尺度数量。

第六步：根据前面预测目标响应值，为此我们可以设定一个阈值tr，当响应最大值y>tr时，则正常更新当前帧(第t帧)的模型即公式(6)；反之，则认为此时的目标区域存在不确定性，不予以更新。

位置滤波器和尺度滤波器均按照式(6)进行更新。

以上仅是本发明的优选实施例，当然不可能限制本发明的范围。因此，在本发明的权利要求中进行的等同变化仍然在本发明的范围内。