基于K-means改进的SMOTE算法的制作方法

本发明涉及smote算法、k-means算法、不平衡数据集的处理及其应用技术领域，尤其是用来实现不平衡数据集的基于k-means改进的smote算法。

背景技术：

smote算法的出现,改进了处理非平衡数据中传统的随机过采样算法,可以有效地对非平衡数据进行纠偏,整体上提高了模型的精度,同时还很大程度上降低了模型的误识率,这是smote算法的优点。其缺陷是没有消除噪声样本，无法确定建模效果的偏差，无法解决非平衡数据的分布问题,容易产生分布边缘化问题,对于边缘的少类样本,对其进行k近邻生成样本也位于边缘且会越来越边缘化,这会使得正负样本的边界越来越模糊,加大样本分类的难度。

技术实现要素：

本发明是为了解决smote算法无法消除噪声样本,容易产生分布边缘化问题,对于边缘的少类样本,对其进行k近邻生成样本也位于边缘且会越来越边缘化,这会使得正负样本的边界越来越模糊,加大样本分类的难度。

实现本发明目的的具体技术方案是：

首先使用k-mean使用算法通过对少数类数据进行聚类操作，选取每个聚类的簇心。这样相当于对少数类数据进行了一个数据的划分，使每个聚类中间的数据相似度最高，且分布均匀，接着修正smote算法的过采样公式。修正后的过采样公式不需要对每一个数据样本选取它的k个最近邻，只需要以每一个簇心为核，每一个聚类内的数据样本为点，进行随机插值。由于在处理不同属性的数据时欧氏距离可能会受到变量量纲的影响,影响距离远近的判断。在本部分使用该方法时,首先对所有变量先进行标准化(即取值减去均值后除以标准差),然后运用该抽样方法得到抽样结果,最后再通过反向标准化(乘以标准差加上均值)进行数据还原,这样能够帮助模型更好地适应原始数据。··

附图说明

通过参考以下结合附图的说明及权利要求书的内容,并且随着对本发明专利的更全面理解,本发明专利的其它目的及结果将更加明白及易于理解。在附图中：

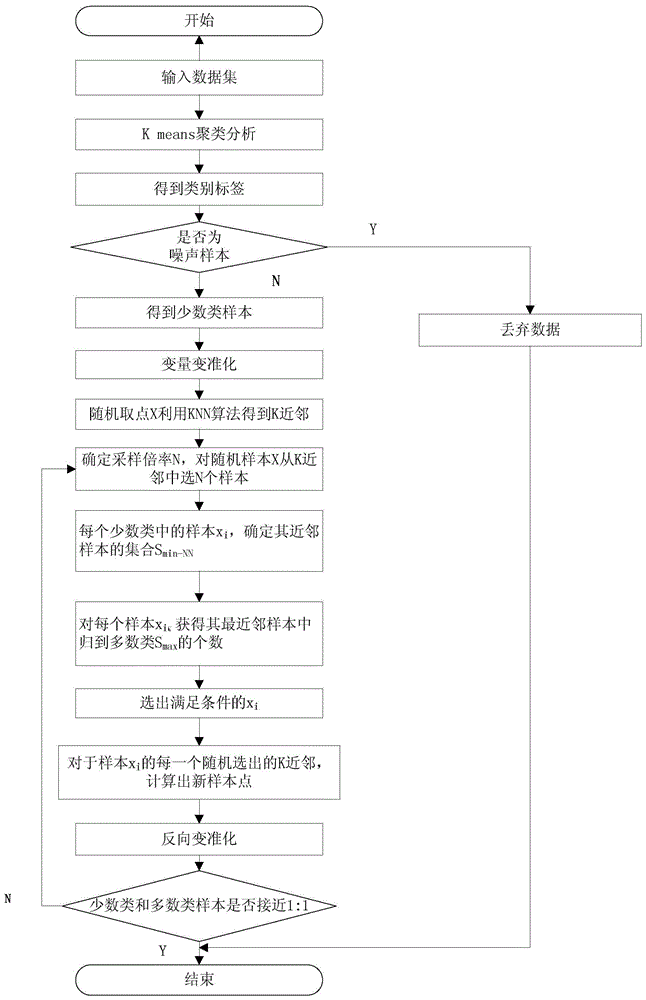
图1为基于k-means算法改进的smote算法流程图；

图2为不同算法对相同数据集处理的召回率对比图

具体实施方式

1、对少数类样本运用基于k-means的聚类算法进行分析，由于基于密度的聚类算法能够很容易识别噪声样本，这样每个样本得到一个类别标签；··

2、剔除基于密度聚类算法识别出来的噪声样本，得到剰余少数类样本；

3、对得到的所有变量先进行标准化(即取值减去均值后除以标准差)，通过计算x到该类样本集所有样本的欧式距离,利用knn算法,选出离样本x最近的k个同类样本点,得到其k近邻。

4、根据正负样本比例确定采样倍率为n,对每一个样本x分别随机从k近邻中选取n个样本,假设选择的近邻为x1,x2,…,xn。

5、对每个少数类中的每一个样本xi，确定其最近邻样本的集合,记为smin-nn,并且smin-nn∈s；

6、针对每个样本xi,获得其最近邻样本中归到多数类smax的个数,根据公式

|smin-nn∩smax|

7、选出满足的xi

8、对于样本xi的每一个随机选出的k近邻(i＝1,2,…,n),新样本计算公式：

式中:xi表示少数类别中的一个样本点；(i＝1,2,…,n)表示从k近邻中随机挑选的样本点；rand(0,1)表示生成0～1之间的随机数。

9、再通过反向标准化(乘以标准差加上均值)进行数据还原

不断进行上述过程，当少数类和多数类样本数量几乎差不多停止。并将改进的算法应用于信用卡欺诈检测中,并通过在信用卡检测数据集上的实验,进一步验证了本发明的可用性。