基于CNN-ARX模型的直线一级倒立摆系统建模方法及模型与流程

本发明涉及工程设计与优化领域，一种可以利用直线一级倒立摆系统的输入输出离散时间序列数据，特别是一种基于cnn-arx模型的直线一级倒立摆系统建模方法。

背景技术：

直线一级倒立摆是一类强非线性、不稳定的、较为复杂的系统，可以采用数据驱动的方式对其进行建模，构建系统输入输出变量的关系模型以描述倒立摆系统的动态特性。状态相依arx模型作为一种非线性建模方法，具有状态相依函数型系数对非线性动态特性的描述能力和自回归结构易于应用于控制的优势，在工业过程系统、金融系统和生态系统等非线性时间序列建模领域有着广泛的应用，采用状态相依arx模型对倒立摆系统建模的核心问题之一就是寻找合适的状态相依函数型系数的结构，利用神经网络逼近状态相依arx模型的系数可获得更高性能的辨识模型，如rbf-arx，dbn-arx等，理论上神经网络在网络层次足够深的情况下，可以拟合任意复杂的非线性关系，而实际应用中，神经网络有可能存在欠拟合、过拟合以及梯度消失等问题。

卷积神经网络(cnn)是一种具有局部连接、权重共享等特性的深层前馈神经网络，这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性。该网络模型具有较强的非线性特征提取能力，且与传统神经网络相比，卷积神经网络的参数更少，能避免传统神经网络参数优化时收敛速度慢的局限性。目前卷积神经网络已成功应用于语音识别、文本处理和图像识别等领域。

技术实现要素：

本发明所要解决的技术问题是，结合状态相依arx模型与卷积神经网络，提供一种基于cnn-arx模型的直线一级倒立摆系统建模方法，提高倒立摆系统辨识模型的预测精度与鲁棒性。

为解决上述技术问题，本发明所采用的技术方案是：一种基于cnn-arx模型的直线一级倒立摆系统建模方法，包括以下步骤：

1)根据直线一级倒立摆系统结构选择u(t)＝a(t),y(t)＝θ(t)，其中小车的加速度a为直线一级倒立摆系统的输入，摆杆顺时针方向偏离竖直向上方向的角度θ为直线一级倒立摆系统的输出，利用系统的输入输出离散时间序列数据构建直线一级倒立摆的cnn-arx模型；模型中的cnn由n个模块与全连接层构成，其中第k个模块(1≤k≤n)包括mk个卷积层与一个池化层。选择cnn-arx模型的输入变量阶次p、输出变量阶次q、状态向量阶次d、cnn中模块个数n、模块中的卷积层数mk以及卷积层中卷积核的尺寸与个数；

2)针对长度为n的训练数据，由cnn-arx模型通过前向运算得到预测输出序列以预测输出序列与期望输出序列y＝(y(1),y(2),…y(n))^t的均方差作为优化目标，通过rmsprop算法更新cnn中的权值与偏置，使均方差最小化，得到最优参数；

3)根据上述最优参数，计算cnn-arx模型的预测输出序列及损失函数值

4)重复上述步骤1)～步骤3)，选择损失函数值最小情况下的cnn-arx模型的输入变量阶次p、输出变量阶次q与状态向量阶次d作为cnn-arx模型的当前阶次；

5)重复上述步骤1)～步骤4)，修改cnn中的模块个数、卷积层数以及卷积核的尺寸与个数，比较不同情况下cnn-arx模型的损失函数值，选取损失函数值最小时的cnn结构作为当前cnn结构，获得直线一级倒立摆系统的cnn-arx模型。

步骤1)中，直线一级倒立摆系统的cnn-arx模型的表达式为：

其中，为t时刻一级倒立摆系统的输出值；为t时刻一级倒立摆系统的控制输入值；为高斯白噪声；p和q分别为cnn-arx模型输出、输入回归多项式的阶次；φh(w(t-1))为cnn的输出值；为倒立摆系统t-iy时刻输出量的系数；为倒立摆系统t-iu时刻输入量的系数；x^l为网络的第l层输出，其中表示第l层为cnn第k个模块中的第r个卷积层，lk(down)表示第l层为cnn第k个模块中的池化层；x⁰为cnn-arx模型的输入值即状态向量，d为状态向量的阶次；为网络第l层的第j个特征图；w^l为第l层网络与第l-1层网络之间的权值矩阵，为第l层中第j个特征图对应第l-1层中第i个特征图的权值矩阵即卷积核矩阵，代表卷积操作，m为第l-1层的特征图个数；b^l为网络第l层的偏置，为第l层中第j个特征图对应的偏置；激活函数和f(·)均选择relu函数，池化函数down(·)对大小为n的输入求平均值或者求最大值，使得输出的大小变为原来的1/n，为第l层特征图j对应的乘性偏置；为x^l经过dropout操作后的输出，其中r^l～bernoulli(p)即概率向量服从bernoulli分布，也就是随机生成仅包含0或1的向量以此实现让该层神经元以某一概率停止工作。

步骤2)中，对直线一级倒立摆系统的cnn-arx模型进行前向运算得到预测输出的具体实现过程包括：

a)选取适当的状态向量w(t-1)作为cnn-arx模型的输入，初始化同时通过xavier分布对cnn的参数进行初始化，其中xavier分布是一种可自动选取分布范围的均匀分布，它保证了输入输出数据的均值以及方差一致，可以加快网络的收敛；

b)令k＝1；

c)令r＝1；

d)计算卷积层输出

e)重复步骤d)直到r＝mk；

f)计算池化层输出

g)根据cnn结构中模型个数，重复c)d)e)f)直到k＝n；

h)对隐含层输出使用dropout后得到其中r^l～bernoulli(p)；即概率向量服从bernoulli分布，也就是随机生成仅包含0或1的向量以此实现让该层神经元以某一概率停止工作；

i)计算cnn网络输出

j)利用cnn前向运算得到的输出值φh(w(t-1))计算倒立摆系统模型的输出值y(t)。

cnn-arx模型的损失函数为：其中，为cnn-arx模型的期望输出，n为训练样本个数。

根据下式更新cnn的参数w′：其中α为学习率，由于全连接层中引入了dropout操作，模型训练时会随机丢弃一些神经元，但测试时无法随机丢弃神经元，否则会导致输出结果不稳定。将训练好的参数w′乘上概率作为测试时的网络参数以保证测试数据与训练数据的一致性。

步骤5)中得到的cnn-arx模型的表达式为：

其中，φh(w(t-1))(h＝0,1,…,p+q)为cnn前向运算得到的输出值。

本发明还提供了一种直线一级倒立摆系统模型，该模型的表达式为：

其中，为t时刻一级倒立摆系统的输出值；为t时刻一级倒立摆系统的控制输入值；为高斯白噪声；p和q分别为cnn-arx模型输出、输入回归多项式的阶次；φh(w(t-1))为cnn的输出值；为倒立摆系统t-iy时刻输出量的系数；为倒立摆系统t-iu时刻输入量的系数；x^l为网络的第l层输出；表示第l层为cnn第k个模块中的第r个卷积层；lk(down)表示第l层为cnn第k个模块中的池化层；x⁰为cnn-arx模型的输入值，即状态向量；d为状态向量的阶次；为网络第l层的第j个特征图；w^l为第l层网络与第l-1层网络之间的权值矩阵；为第l层中第j个特征图对应第l-1层中第i个特征图的权值矩阵即卷积核矩阵，代表卷积操作，m为第l-1层的特征图个数；b^l为网络第l层的偏置，为第l层中第j个特征图对应的偏置；激活函数和f(·)均选择relu函数，池化函数down(·)对大小为n的输入求平均值或者求最大值，使得输出的大小变为原来的1/n，为第l层特征图j对应的乘性偏置；为x^l经过dropout操作后的输出，其中r^l～bernoulli(p)，即概率向量服从bernoulli分布，也就是随机生成仅包含0或1的向量以此实现让该层神经元以某一概率停止工作。

作为一个发明构思，本发明还提供了一种用于预测直线一级倒立摆系统输出的cnn-arx模型，该模型的输入为t时刻一级倒立摆系统的控制输入值该模型表达式为：

其中，为t时刻一级倒立摆系统的输出值；为高斯白噪声；p和q分别为cnn-arx模型输出、输入回归多项式的阶次；φh(w(t-1))为cnn的输出值；为倒立摆系统t-iy时刻输出量的系数；为倒立摆系统t-iu时刻输入量的系数；x^l为网络的第l层输出；表示第l层为cnn第k个模块中的第r个卷积层；lk(down)表示第l层为cnn第k个模块中的池化层；x⁰为cnn-arx模型的输入值，即状态向量；d为状态向量的阶次；为网络第l层的第j个特征图；w^l为第l层网络与第l-1层网络之间的权值矩阵；为第l层中第j个特征图对应第l-1层中第i个特征图的权值矩阵即卷积核矩阵，代表卷积操作，m为第l-1层的特征图个数；b^l为网络第l层的偏置，为第l层中第j个特征图对应的偏置；激活函数和f(·)均选择relu函数，池化函数down(·)对大小为n的输入求平均值或者求最大值，使得输出的大小变为原来的1/n，为第l层特征图j对应的乘性偏置；为x^l经过dropout操作后的输出，其中r^l～bernoulli(p)，即概率向量服从bernoulli分布，也就是随机生成仅包含0或1的向量以此实现让该层神经元以某一概率停止工作。

与现有技术相比，本发明所具有的有益效果为：本发明综合了状态相依arx模型对非线性系统的描述能力和cnn(卷积神经网络)的特征提取能力，提出了一种基于cnn-arx模型的直线一级倒立摆系统建模方法。在cnn中使用relu激活函数在很大程度上避免了梯度消失和爆炸的问题；采用dropout(随机失活)技术，在学习过程中通过将隐含层的输出随机归零，降低节点间的相互依赖性，从而实现网络的正则化，减小网络过拟合的风险，有效提高非线性系统辨识模型的预测精度和鲁棒性；本发明提出的cnn-arx模型可以用于直线一级倒立摆系统的数据建模、数据预测以及基于模型的直线一级倒立摆系统控制器设计等领域，具有较高的价值和应用前景。

附图说明

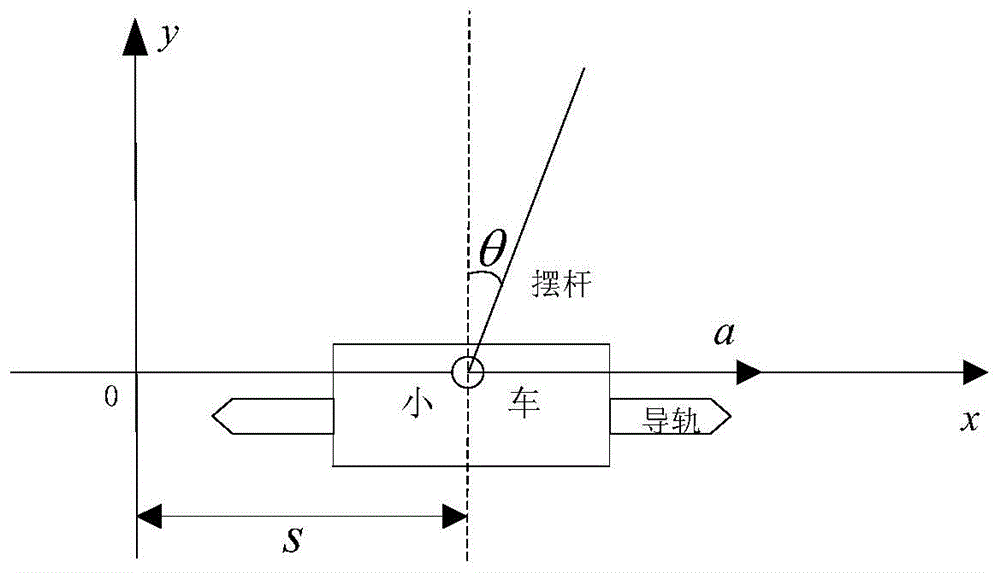
图1为直线一级倒立摆系统结构图；

图2为本发明中cnn-arx模型参数辨识流程图；

图3为本发明中cnn-arx模型结构示意图。

具体实施方式

1)本发明从直线一级倒立摆系统的结构入手，直线一级倒立摆系统的输入为小车的加速度a，输出为摆杆顺时针方向偏离竖直向上方向的角度θ、小车距离启动位置的位移s，而直线一级倒立摆的摆杆角度θ与小车位移s之间无互相依赖关系，故可对小车位移s直接使用物理公式建模。选择u(t)＝a(t),y(t)＝θ(t)，利用系统的输入输出离散时间序列数据构建直线一级倒立摆的cnn-arx模型；选定状态向量w(t-1)＝[y(t-1),y(t-2),…,y(t-d)]^t，选择cnn-arx模型的输入变量阶次p、输出变量阶次q、状态向量阶次d、cnn中模块个数n、各个模块中的卷积层数mk以及卷积层中卷积核的尺寸与个数，构建初始的cnn-arx模型：

其中，为t时刻一级倒立摆系统的输出值；为t时刻一级倒立摆系统的控制输入值；为高斯白噪声；p和q分别为cnn-arx模型输出、输入回归多项式的阶次；φh(w(t-1))为cnn的输出值；为倒立摆系统t-iy时刻输出量的系数；为倒立摆系统t-iu时刻输入量的系数；x^l为网络的第l层输出，其中表示第l层为cnn第k个模块中的第r个卷积层，lk(down)表示第l层为cnn第k个模块中的池化层；x⁰为cnn-arx模型的输入值即状态向量，d为状态向量的阶次；为网络第l层的第j个特征图；w^l为第l层网络与第l-1层网络之间的权值矩阵，为第l层中第j个特征图对应第l-1层中第i个特征图的权值矩阵即卷积核矩阵，代表卷积操作，m为第l-1层的特征图个数；b^l为网络第l层的偏置，为第l层中第j个特征图对应的偏置；激活函数和f(·)均选择relu函数，池化函数down(·)对大小为n的输入求平均值或者求最大值，使得输出的大小变为原来的1/n，为第l层特征图j对应的乘性偏置；为x^l经过dropout操作后的输出，其中r^l～bernoulli(p)。

2)完成直线一级倒立摆系统cnn-arx模型的初步构造后，对该模型进行前向运算，前向运算过程如下：

输入：状态向量w(t-1)

过程：

a):初始化x⁰＝w(t-1)＝[y(t-1),y(t-2),…,y(t-d)]^t，定义本层的输入维度为n，输出维度为m，利用xavier分布初始化cnn参数，使网络参数均匀分布于区间xavier初始化方法在很大程度上保证了输入输出数据的均值以及方差一致，加快了网络的收敛。

b):对cnn进行前向运算，根据选定的cnn结构计算不断计算卷积层输出以及池化层输出对隐含层输出使用dropout后得到其中r^l～bernoulli(p)；接着计算cnn网络输出利用cnn前向运算得到的输出值φh(w(t-1))计算倒立摆系统模型的输出值y(t)。

输出：预测值y(t)

得到输出y(t)后，构造结构风险损失函数如下：

其中，为直线一级倒立摆系统的期望输出，n为训练样本个数。通过rmsprop算法最小化损失函数e并不断更新模型的参数w′；

rmsprop算法(即均方根反向传播算法)为每个参数选择不同的学习率，该算法能有效抑制梯度的锯齿下降，rmsprop算法的迭代公式如下：

其中ε为全局学习率，gt为一批m个数据的梯度，r为梯度平方的指数平均值，m表示每次选择数据的样本大小，超参数ρ为衰减速率，用于控制移动平均的长度范围，θ为待辨识模型中的参数，小常数δ用于数值稳定，一般设置为10^-6。通过rmsprop优化器不断更新参数直到损失函数达到要求或者不再降低，即得到了模型的最优参数。

3)在得到最优参数的情况下计算cnn-arx模型的预测输出序列及损失函数值

4)选择不同阶次情况下损失函数最小时的输入变量阶次p、输出变量阶次q与状态向量阶次d作为当前模型阶次；

5)改变cnn结构，如修改cnn中的模块个数、卷积层数以及卷积核的尺寸与个数等，比较在当前阶次下不同cnn结构的损失函数大小，并选取损失函数值为最小情况下的结构作为当前cnn结构，获得直线一级倒立摆的cnn-arx模型；

6)最终得到的直线一级倒立摆系统cnn-arx模型的表达式如下：

其中，φh(w(t-1))(h＝0,1,…,p+q)为cnn前向运算得到的输出值。

综上可得，本发明综合了带外生变量的状态相依自回归模型对非线性系统的描述能力和卷积神经网络的特征提取能力，相比于现有的直线一级倒立摆系统建模方法而言，有效提高了模型的预测精度和鲁棒性，具有较高的价值和应用前景。