一种空化水射流喷嘴结构设计方法与流程

本发明涉及属于金属表面强化、表面清洗领域，具体涉及一种空化水射流喷嘴结构设计方法。

背景技术：

空化水射流技术是利用高速水射流产生的大量微小空泡群，空泡群在固体边界附近溃灭时产生高达上千mpa的冲击压强和微射流，可用于清洗、表面强化等，具有环保、节能、高效、易操作等特点。喷嘴设计人员通常选用圆形、椭圆形、正方形、锥形等作为传统空化喷嘴截面，并采用试错法进行选型设计，虽然已在数值模拟和试验研究方面取得了很多成果，但结构设计理论基础不足，喷嘴结构仍不够优化。

技术实现要素：

本发明目的是为了克服现有技术的不足而提供一种空化水射流喷嘴结构设计方法。

为达到上述目的，本发明所采用的技术方案为：

一种空化水射流喷嘴结构设计方法，所述设计方法依次包括如下步骤：

①、根据伯努利原理计算流体中某点的压强与该点处流体横截面直径之间的比例关系；

②、根据步骤①中的比例关系，计算处于空化水射流喷嘴内的流体压降与缩颈长度之间的比例关系；

③、根据步骤②中的比例关系，在喷嘴内流体压强随运动距离呈连续函数变化时，计算喷嘴横截面内径与缩颈长度之间的函数关系。

优选地，步骤①中流体中某点的压强与该点处流体横截面直径的四次方呈反比关系。

优选地，步骤②中喷嘴内的流体压降与缩颈长度的4次方倒数呈正比关系。

优选地，步骤③中的喷嘴内流体压强随缩颈长度呈连续函数变化包括：一、流体压强随缩颈长度呈等比例变化；二、流体压强随缩颈长度呈线性变化。

优选地，步骤①中比例关系计算方法如下：根据努利原理计算公式，p+0.5ρv²+ρgh＝c

式中，p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，c是一个常量，变形后得，

p＝c-0.5ρv²-ρgh

将流速v＝q/s(q为流量，s为截面面积)代入上式得，

对于圆形截面喷嘴，s＝πd²/4，d为截面直径，代入上式得，

计算出流体中某点的压强p与喷嘴截面直径d的四次方呈反比关系。

优选地，步骤②中比例关系计算方法如下：设流体在喷嘴入口端盒出口端的流速、压强、水头分别为v1、p1、h1和v2、p2、h2，则压降为，

喷嘴垂直放置时，h1-h2＝l，即

喷嘴水平放置时，则

优选地，步骤③中喷嘴横截面内径d与缩颈长度l之间的函数关系p＝f(l):根据

可得,

优选地，在流体压强p随缩颈长度l呈等比例变化情况下,喷嘴横截面内径d与缩颈长度l之间的函数关系：根据其中k1为比例常数，

变形可得，

优选地，在流体压强p随缩颈长度l呈线性变化情况下,喷嘴横截面内径d与缩颈长度l之间的函数关系：l＝k2-k3p²或其中k2，k3为常数，

则

可得，

由于以上技术方案的实施，本发明与现有技术相比具有如下优点：

本发明从水流的伯努利原理出发，根据理论推导计算，以定量控制喷嘴出入口水压变化为基础，设计喷嘴出入口截面直径与长度之间关系，可获得水压等比变化、连续变化及阶梯变化的喷嘴结构，可为喷嘴设计人员提供设计方法和思路并提供选型理论基础和依据。为进一步优化喷嘴结构，提高空化效率夯实基础。

附图说明

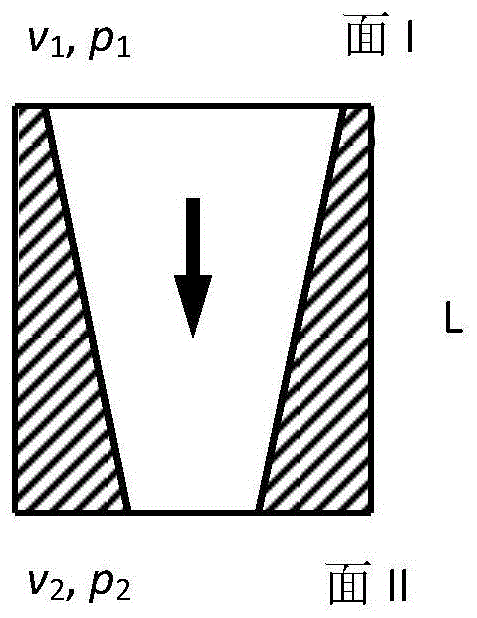
图1空化泡形成缩颈位置微单元结构示意图；

图2压力随缩颈长度呈线性下降时喷嘴内径与缩颈长度关系曲线；

图3压力随缩颈长度呈先慢后快抛物线型下降时喷嘴内径与缩颈长度关系曲线；

图4喷嘴内径与长度呈台阶串联变化的缩颈结构示意图。

具体实施方式

下面结合附图和具体的实施例对本发明做进一步详细的说明。

如图1至图4所示，根据伯努利原理，对于定常流(在流动系统中，流体在任何一点之性质不随时间改变)、不可压缩流(密度为常数)、无摩擦流(摩擦效应可忽略，忽略黏滞性效应)、流体沿着流线流动的流体，在任意位置满足如下关系：

p+0.5ρb²+ρgh＝c

式中，p为流体中某点的压强，v为流体该点的流速，ρ为流体密度，g为重力加速度，h为该点所在高度，c是一个常量。变形后得：

p＝c-0.5ρv²-ρgh

将流速v＝q/s(q为流量，s为截面面积)代入上式得：

对于圆形截面喷嘴，s＝πd²/4，d为截面直径，代入上式得：

可以看出流体中某点的压强p与喷嘴截面直径d的四次方呈反比关系。

如图1所示，空化现象发生的关键因素在喷嘴结构的缩颈(喷嘴横截面变化)，假设喷头缩颈前为i，缩颈后为ii，液体从i截面流入，ii截面流出，假设i和ii截面液流的流速、压力、水头分别为v1、p1、h1和v2、p2、h2，则压降为：

垂直放置时，h1-h2＝l，即

水平放置时，则

由于实验过程中进口端水压往往为数十mpa，出口端压力很低，接近大气压，因此压降(p1-p2)很大。喷嘴高度h一般为10-20mm左右，ρgl值约为0.0001-0.0002mpa，其值很小，可以忽略。根据质量守恒，在两处的流量相等，假设水的密度不变，或密度变化影响可忽略，则对于空化水射流喷嘴，压力下降可认为仅与喷嘴内径有关，即与缩颈长度的4次方的倒数呈正比。

在空化水射流生成空穴过程中，需要在缩颈处水压下降到某一范围内。对于不同截面形状，压力下降速率不同，从而导致出水空化效果不同。采用控制压力随缩颈长度下降速率的方法，可以为设计人员提出一种新思路，具体如下：

采用压力随缩颈长度呈连续函数变化p＝f(l)设计喷嘴截面内径d与缩颈长度l的关系，使得压力升降的值按照特定规律变化。即：

可得，

一、流体压强随缩颈长度呈等比例变化(参见图2)；即

k1为比例常数，变形得：

故，喷嘴截面内径d随缩颈长度l呈四次方倒数关系，即：

或d＝(a2*l+b2)^-1/4

其中

举例一：试验用高压泵加载水压p为30mpa，水密度ρ为1000kg/m³，流量q为2m³/h，喷嘴进口直径10mm＝0.01m，水平放置，高度h为0，喷嘴进口段缩颈长度l为20mm，内径为2mm，则：

当l＝0时，p0＝30mpa，

常量c为：

当l＝20mm时，d＝2mm有

求得k1＝781250000

则

则曲线方程变为：d＝(3119639062500*l+99828450)^-1/4

二、流体压强随缩颈长度呈线性变化(参见图3)，即l＝k2-k3p²或k2，k3为常数，则

可得，

举例二：

当l＝0时，p＝30mpa，即

当l＝20mm时，d＝2mm，同上，有p＝14375000，即

解得，k2＝0.02596，k3＝2.884*10^-17

此外，本发明也适用于采用不连续函数设计喷嘴截面内径与缩颈长度的关系，形成台阶串联结构，如图4所示。

综上所述，本发明从水流的伯努利原理出发，根据理论推导计算，以定量控制喷嘴出入口水压变化为基础，设计喷嘴出入口截面直径与长度之间关系，可获得水压等比变化、连续变化及阶梯变化的喷嘴结构，可为喷嘴设计人员提供设计方法和思路并提供选型理论基础和依据。为进一步优化喷嘴结构，提高空化效率夯实基础。

上述实施例只为说明本发明的技术构思及特点，其目的在于让熟悉此项技术的人士能够了解本发明的内容并据以实施，并不能以此限制本发明的保护范围，凡根据本发明精神实质所作的等效变化或修饰，都应涵盖在本发明的保护范围之内。