一种量子平均池化计算方法与流程

本发明涉及语音分析和图像识别领域的量子神经网络计算技术领域，尤其是一种量子平均池化计算方法。

背景技术：

卷积神经网络是一种特殊的人工神经网络，目前已经成为语音分析和图像识别领域最常使用的工具之一，因此也是人工神经网络研究热点。hubeldh等人通过对猫的视觉皮层进行研究发现每个单个神经元不会对整个图像做出回应，而只对其负责的感受野(receptivefiled)做出响应。fukushimak等人在感受野概念的基础上首次提出神经认知机(neocognitron)模型，被公认为是第一个卷积神经网络(cnn)模型。lecuny等提出lenet-5模型，由卷积层、下采样、全链接层构成卷积神经网络，在手写体数字识别实验上取得巨大成功。krizhevskya等人提出alexnet的出现标志着神经网络的复苏和深度学习的崛起。hek等人提出resnet的在imagenet图片分类竞赛上表现超过人类水准的算法。

2006年，研究人员成功利用gpu加速了cnn，相比cpu运算速率快了4倍。但随着数据量的增加，gpu也将无法满足卷积神经网络的计算需求，有必要提出一种新的计算方法应对计算能力的无限提升。依据cnn原理及量子计算的并行计算能力，许兴阳等人构建了量子门组卷积神经网络(qgcnn)模型，congi等人引入量子卷积神经网络(qcnn)量子线路模型，将cnn关键特性扩展到了量子域。qcnn由卷积层、池化层、全链接层构成，不断的执行卷积层池化层直到系统足够小，全链接层作用于最后剩余量子比特，最后通过测量固定数量的输出量子位获得线路结果。基于qcnn量子线路模型，结合量子通用门构建了量子平均池化线路模型。

标准cnn模型通常由卷积层、池化层、非线性激活层以及全链接层构成，卷积层对输入信息进行特征提取，池化层依据池化核的大小及步长对卷积输出结果信息进行维度的减小和增加平移不变性，池化分为最大池化与平均池化。

技术实现要素：

本发明的目的就是针对上述情况提出一种量子平均池化计算方法，该计算方法具有经典计算机无法比拟的超级计算能力，为人工智能、深度学习卷积神经网络等大规模计算难题提供解决方案。

本发明的具体方案是：一种量子平均池化计算方法，具体包括以下步骤：

1)将量子卷积结果信息|fn>长宽各n-qbit，按行展开得到|f2n>＝(c0,c1,c2,…,c2n)^t作为输入信息，再将量子态|f2n>输入进搭建好的量子平均池化线路模型中；

2)经交换门d2n作用，|f2n>量子态基态的位置发生改变；

3)在第1量子比特与第2n量子比特通过h门作用，其余量子比特经单位阵作用，在此时刻有操作，得到加减相加的量子态基态，其中表示张量积；

4)通过作用后的量子态测量，当测量结果为|00>态时输出量子平均池化结果。

进一步的，本发明中所述交换门d2n为矩阵结构，其是为了完成两个量子比特a和b状态的互换，交换门在计算基态|a,b>上的一系列作用为：

其中表示模2加法。

进一步的，本发明中所述h门矩阵表述为：

进一步的，本发明中卷积结果信息|fn>共含有n个量子比特，n＝2ⁿ个状态，记为|i>表示信息的位置，ci表示在i处的概率幅值，满足归一化条件。

本发明中，通过多量子比特通用门搭建量子平均池化线路模型，输出平均池化结果，对卷积后的结果信息进行下采样处理、减少参数维度，更有利于信息传输到下一模块进行特征提取；同时利用量子相干叠加的方式实现了信息的高效存储和并行处理，具有经典计算机无法比拟的超级计算能力，为人工智能、深度学习卷积神经网络等大规模计算难题提供解决方案。

附图说明

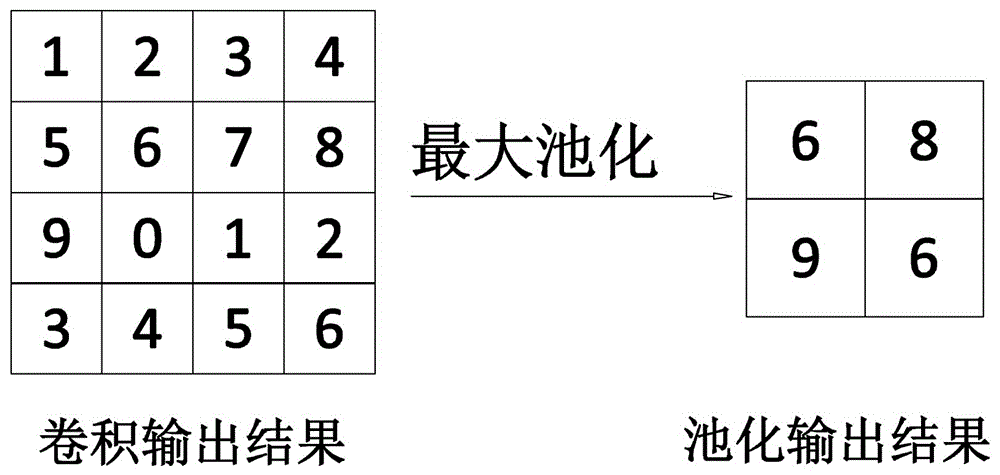
图1是经典池化计算中的池化核大小为2*2，步长为2的最大池化计算示例示意图；

图2是经典池化计算中的池化核大小为2*2，步长为2的平均池化计算示例示意图；

图3是本发明中2n-qbit量子平均池化线路模型示意图；

图4是本发明中交换门量子线路等价框图；

图5是本发明中交换门真值表；

图6是本发明中两量子比特h门线路示意图；

图7是本发明的一种实施例4-qbit量子平均池化线路模型示意图；

图8是本发明的一种实施例4-qbit平均池化中量子态交换门真值表；

图9是本发明的一种实施例4-qbit量子平均池化示意图；

图10是本发明的第二种实施例6-qbit量子平均池化线路模型示意图；

图11是本发明的第二种实施例6-qbit平均池化中量子态交换门真值表；

图12是本发明的第二种实施例6-qbit量子平均池化示意图；

图13是本发明的第三种实施例8-qbit量子平均池化线路模型示意图。

具体实施方式

本发明是一种量子平均池化计算方法，具体包括以下步骤：

1)将量子卷积结果信息|fn>长宽各n-qbit，按行展开得到|f2n>＝(c0,c1,c2,…,c2n)^t作为输入信息，再将量子态|f2n>输入进搭建好的量子平均池化线路模型中；

2)经交换门d2n作用，|f2n>量子态基态的位置发生改变；

3)在第1量子比特与第2n量子比特通过h门作用，其余量子比特经单位阵作用，在此时刻有操作，得到加减相加的量子态基态，其中表示张量积；

4)通过作用后的量子态测量，当测量结果为|00>态时输出量子平均池化结果。

进一步的，本实施例中所述交换门d2n为矩阵结构，其是为了完成两个量子比特a和b状态的互换，交换门在计算基态|a,b>上的一系列作用为：

其中表示模2加法，交换门如图4所示，输入输出量子真值表如图5所示。

例如记交换门矩阵表述为dn，n表示含有的量子比特数，则

进一步的，本实施例中所述h门矩阵表述为：

进一步的，本实施例中卷积结果信息|fn>共含有n个量子比特，n＝2ⁿ个状态，记为|i>表示信息的位置，ci表示在i处的概率幅值，满足归一化条件。

在上述过程中h门矩阵表述为

将h门放置在图6的量子线路上，量子线路中的量子态随时间发生演化，在第2个量子态遇到h门时而被操作，而此时的第1个量子比特执行单位阵操作状态不发生改变。在该时刻下两量子比特纠缠态遇到矩阵表述为

下面结合具体的计算实施过程来进行具体的说明。

实施例1：4-qbit量子信息平均池化计算：

如图9所示，卷积结果信息长宽各为2-qbit，共含有4-qbit量子信息，将其按行展开记为量子态|f4>，|f4>＝(c0,c1,c2,c3,c4,c5,c6,c7,c8,c9,c10,c11,c12,c13,c14,c15)^t。以设定的平均池化核对卷积结果信息进行平均池化操作，输出共含有2-qbit平均池化结果，记为|g2>＝(d0,d1,d2,d3)^t，取部分值进行说明，即

为求得上述平均池化结果|g2>，将量子态|f4>输入如图7所示的量子平均池化线路模型中，量子态|f4>首先经交换门d4作用后量子态基态位置发生交换，量子态交换门操作如图8所示真值表表格进行，其中d4矩阵表述为d4·|f4>是经交换门作用后的量子比特状态，其矩阵表述为(c0,c1,c4,c5,c2,c3,c6,c7,c8,c9,c12,c13,c10,c11,c14,c15)^t。将h门作用在第一和最后一个量子比特上，其余量子比特进行单位阵即得到矩阵表述为

为了输出全为相加的量子态，需要对结果进行测量，当测量结果输出为|00>时则满足结果所需，输出结果矩阵表述为

因输出结果为量子态信息，当对量子比特进行测量时其状态会以一定概率坍缩到|0>或|1>上，此时的结果信息也即被破坏，应用到量子卷积神经网络池化层的设计时无需对其输出结果进行测量。平均池化计算中需对每个数值对应求和，并计算其平均值，因此在量子计算中输出|g2>＝(d0,d1,d2,d3)^t。

实施例2：6-qbit量子信息平均池化计算：

长宽各3-qbit的卷积结果信息|f6>经平均池化核操作后得到池化结果信息|g4>，量子平均池化示意图如图12，取部分值进行说明即

首先将量子态|f6>＝(c0,c1,c2,c3,c4,c5,c6,c7,…,c60,c61,c62,c63)^t输入进量子线路模型图10中，经3量子比特的交换门操作使得量子态基态位置发生改变，变化后的量子态为(c0,c1,c8,c9,c2,c3,c10,c11,…,c54,c55,c62,c63)^t，具体交换门操作真值表如图11表格所示。在下一时刻，交换过的量子态经h门及单位阵作用后，以每相邻的四个基矢加减作用成为一个新的量子态基态，且新的量子态基态每四个为一小组构成了作用后的量子态，新的量子态矩阵表述为为了输出全为相加的量子态基态，对量子比特进行测量，当测量结果为|00>时输出量子平均池化结果将结果简记为|g4>＝(d0,d1,d2,…,d15)^t。

实施例3：8-qbit量子信息平均池化计算：计算方法同实施例1和实施例2的计算方法相同，8-qbit量子平均池化线路模型如图13所示。

通过上述实施例1、实施例2和实施例3的计算过程，可以推广到2n-qbit量子平均池化线路模型中，如图3所示，量子卷积结果信息长宽各n-qbit，按行展开得到|f2n〉＝(c0,c1,c2,…,c2n)^t作为输入信息，得到量子平均池化结果需通过以下步骤：

1)、将量子态|f2n>输入进搭建好的量子平均池化线路模型图3中。

2)、经交换门d2n作用，|f2n>量子态基态的位置发生改变。

3)、在第1量子比特与第2n量子比特通过h门作用，其余量子比特经单位阵作用，在此时刻有操作，得到加减相加的量子态基态。

4)、通过作用后的量子态测量，当测量结果为|00>态时输出量子平均池化结果。

通过多量子比特通用门搭建量子平均池化线路模型，输出平均池化结果，对卷积后的结果信息进行下采样处理、减少参数维度，更有利于信息传输到下一模块进行特征提取。利用量子相干叠加的方式实现了信息的高效存储和并行处理，具有经典计算机无法比拟的超级计算能力，为人工智能、深度学习卷积神经网络等大规模计算难题提供解决方案。