一种水环境数学模型模拟精度综合评价方法与流程

本发明涉及一种水环境数学模型模拟精度综合评价方法，属于模型模拟技术领域。

背景技术：

随着国民经济的快速发展和各行各业对自然资源需求的急剧增加，水环境问题也日益突出，许多国家和地区都加强了水环境监测、水环境模拟、水环境管理和修复等问题的研究。水环境模型因其具有投资少、运行周期短、效率高、灵活性等优势，在水环境问题的研究中有着十分重要的作用。

水环境模型按照研究对象分类，可分为地表水环境模型、地下水环境模型等。其中，地表水环境质量模型可以模拟和预测水流、水质、泥沙等运动规律，为环境管理决策提供技术支持。地表水环境质量模型是识别地表水环境问题、研究污染物在地表水环境中演化规律的不可或缺的工具，它是环境管理决策的重要依据。

当前水环境模型成为水环境定量化管理中的重要工具,如efdc、wasp、mike等复杂的机理模型在各类水体中得到了大量应用。为了使机理模型能够更为详细地体现水体中污染物的迁移转化过程,对模型的模拟精度要求也越来越高，因此，建立水环境模型模拟精度评价体系具有重要意义。目前水环境数学模型模拟精度评价的分析尚缺乏统一的评价指标体系，大多只通过一个简单的指标进行判定。

技术实现要素：

本发明的目的在于提供一种水环境数学模型模拟精度综合评价方法，以解决现有技术中存在的传统水环境模型模拟精度评价方法考虑不全面、大多只通过一个简单的指标进行判定的缺点。

为实现上述目的，本发明采用如下技术方案：

一种水环境数学模型模拟精度综合评价方法，包括如下步骤：

确定反映模型模拟精度的评价指标；

确定用于评价模型水动力模拟精度的水动力评价因子；

确定用于评价模型水质模拟精度的水质评价因子；

选取模型模拟精度评价点位；

设定模拟时长，以相同时间频率获取各评价点位上水动力评价因子和水质评价因子的实测值、模拟值；

根据获取的各评价点位上水动力评价因子的实测值、模拟值，计算各评价点位上水动力评价因子的评价指标；

根据获取的各评价点位上水质评价因子的实测值、模拟值，计算各评价点位上水质评价因子的评价指标；

根据计算出的各评价点位上水动力评价因子的评价指标，计算模型水动力模拟精度的平均评价指标；

根据计算出的各评价点位上水质评价因子的评价指标，计算模型水质模拟精度的平均评价指标；

根据计算出的模型水动力模拟精度和模型水质模拟精度的平均评价指标，对水环境数学模型模拟精度进行综合评价分析。

进一步地，所述评价指标包括：相对误差、决定系数、纳什效率系数。

进一步地，所述各评价点位上水动力评价因子的评价指标通过以下公式计算得到：

式(1)中，i为水动力评价因子，rei为水动力评价因子相对误差，mia为水动力评价因子模拟平均值，sia为水动力评价因子实测平均值；式(2)中，ri²为水动力评价因子决定系数，mij为水动力评价因子第j时间模拟值，sij为水动力评价因子第j时间实测值，n为模拟时长；式(3)中，nsei为水动力评价因子纳什效率系数。

进一步地，所述各评价点位上水质评价因子的评价指标通过以下公式计算得到：

式(1’)中，g为水质评价因子，reg为水质评价因子相对误差，mga为水质评价因子模拟平均值，sga为水质评价因子实测平均值；式(2’)中，rg²为水质评价因子决定系数，mgj为水质评价因子第j时间模拟值，sgj为水质评价因子第j时间实测值，n为模拟时长；式(3’)中，nseg为水质评价因子纳什效率系数。

进一步地，所述模型水动力模拟精度的平均评价指标通过以下公式计算得到：

式(4)中，i为水动力评价因子，k为评价点位，m为评价点位个数，reik为评价点位k上水动力评价因子i的相对误差，reia为水动力评价因子i的平均相对误差；式(5)中，rik²为评价点位k上水动力评价因子i的决定系数，ria²为水动力评价因子i的平均决定系数；式(6)中，nseik为评价点位k上水动力评价因子i的纳什效率系数，nseia为水动力评价因子i的平均纳什效率系数；式(7)中，rea为水动力模拟平均相对误差，h为水动力评价因子个数；式(8)中，ra²为水动力模拟平均决定系数；式(9)中，nsea为水动力模拟平均纳什效率系数。

进一步地，所述模型水质模拟精度的平均评价指标通过以下公式计算得到：

式(4’)中，g为水质评价因子，k为评价点位，m为评价点位个数，regk为评价点位k上水质评价因子g的相对误差，rega为水质评价因子g的平均相对误差；式(5’)中，rgk²为评价点位k上水质评价因子g的决定系数，rga²为水质评价因子g的平均决定系数；式(6’)中，nsegk为评价点位k上水质评价因子g的纳什效率系数，nsega为水质评价因子g的平均纳什效率系数；式(7’)中，rea’为水质模拟平均相对误差，z为水质评价因子个数；式(8’)中，ra’²为水质模拟平均决定系数；式(9’)中，nsea’为水质模拟平均纳什效率系数。

进一步地，所述水动力评价因子包括流量和水位。

进一步地，所述水质评价因子包括氨氮、cod、总磷中的至少一个。

与现有技术相比，本发明具有以下优点：

本发明建立了一套全新的水环境数学模型模拟精度综合评价方法，综合考虑相对误差、决定系数、纳什效率系数三个评价指标，克服了传统评价方法中考虑不全面的缺点，客观、科学地对水环境数学模型模拟精度进行评价，使评价结果更为全面和客观。

附图说明

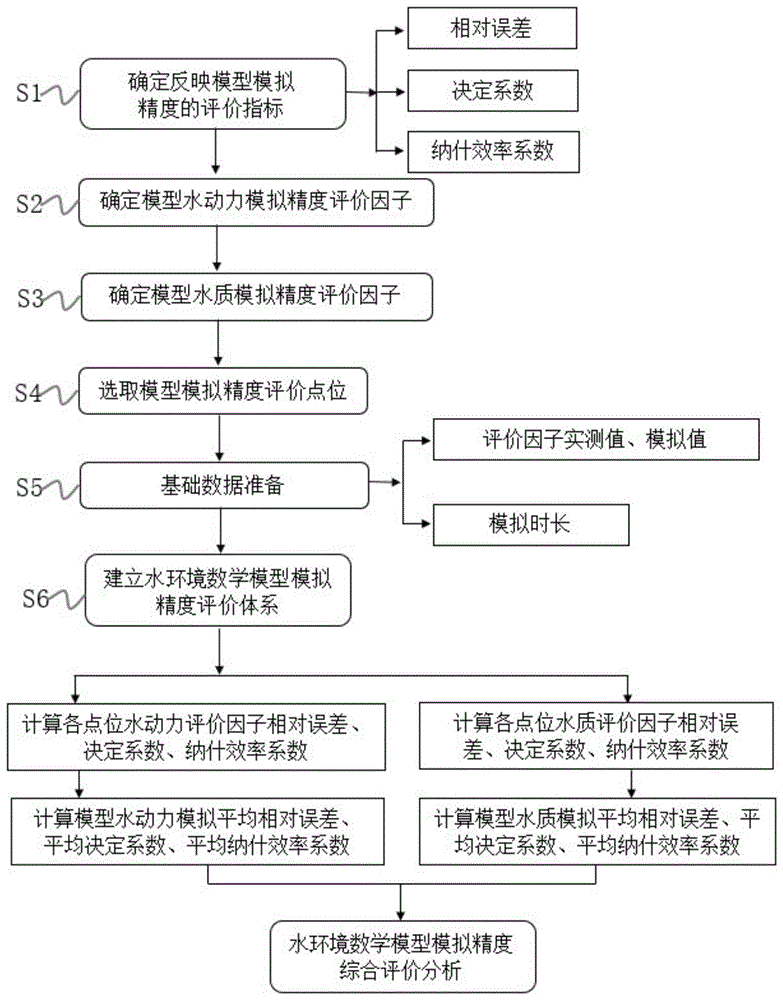
图1为本发明实施例的一种水环境数学模型模拟精度综合评价方法的流程示意图。

具体实施方式

下面结合具体实施例对本发明作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

如图1所示，一种水环境数学模型模拟精度综合评价方法，包括如下步骤：

s1.确定反映模型模拟精度的评价指标：相对误差、决定系数、纳什效率系数；

s2.确定模型水动力模拟精度评价因子(水动力评价因子)；

s3.确定模型水质模拟精度评价因子(水质评价因子)；

s4.选取模型模拟精度评价点位；

s5.基础数据准备：设定模拟时长，以相同时间频率获取各评价点位上水动力评价因子和水质评价因子的实测值、模拟值；

s6.建立水环境数学模型模拟精度评价体系。

其中，步骤s6具体包括以下步骤：

a1.根据获取的各评价点位上水动力评价因子的实测值、模拟值，计算各评价点位上水动力评价因子的相对误差、决定系数、纳什效率系数；

a2.根据获取的各评价点位上水质评价因子的实测值、模拟值，计算各评价点位上水质评价因子的相对误差、决定系数、纳什效率系数；

a3.根据计算出的各评价点位上水动力评价因子的相对误差、决定系数、纳什效率系数，计算模型水动力模拟精度的平均相对误差、决定系数、纳什效率系数；

a4.根据计算出的各评价点位上水质评价因子的相对误差、决定系数、纳什效率系数，计算模型水质模拟精度的平均相对误差、决定系数、纳什效率系数；

a5.根据计算出的模型水动力模拟精度和模型水质模拟精度的平均相对误差、决定系数、纳什效率系数，对水环境数学模型模拟精度进行综合评价分析。

下面以某水环境数学模型模拟结果a为例，阐述本发明实施例的具体实施步骤：

s1.确定反映模型模拟精度的评价指标

本实施例中评价指标包括相对误差、决定系数、纳什效率系数。

s2.确定模型水动力模拟精度评价因子

本实施例中模型水动力模拟精度评价因子包括流量和水位。

s3.确定模型水质模拟精度评价因子

水质模拟精度评价因子需根据实测水质数据与模型水质边界条件决定，选取包含在模型水质边界中且具有实测数据的评价因子，常见评价因子有氨氮、cod、总磷等，评价因子的选取数量至少为一个。本实施例中模型水质模拟精度评价因子选取数量为2个，分别为氨氮和cod。

s4.选取模型模拟精度评价点位

评价点位需根据实际情况决定，选取具有模型水动力模拟精度评价因子实测数据与模型水质模拟精度评价因子实测数据的点位，评价点位的选取数量至少为一个。本实施例中模型模拟精度评价点位选取数量为3个，分别为点位1、点位2、点位3。

s5.基础数据准备

基础数据包括模拟时长、评价点位上水动力评价因子和水质评价因子实测值、模拟值等，评价点位上水动力评价因子和水质评价因子模拟值的输出频率需根据实测值的监测频率与模型精度要求决定，一般输出频率为一分钟一个数据。本实施例中模拟时长为8小时(480分钟)，模拟值的输出频率为一分钟一个数据，共480个数据，各评价点位上水动力评价因子和水质评价因子部分实测值、模拟值数据见表1、表2。

表1

表2

s6.建立水环境数学模型模拟精度评价体系

a1.以选取的模型水动力模拟精度评价因子为输出目标，计算各点位水动力评价因子相对误差、决定系数、纳什效率系数，计算公式如下：

式(1)中，i为水动力评价因子；rei为水动力评价因子相对误差；mia为水动力评价因子模拟平均值；sia为水动力评价因子实测平均值；式(2)中，ri²为水动力评价因子决定系数；mij为水动力评价因子第j分钟(秒或小时)模拟值；sij为水动力评价因子第j分钟(秒或小时)实测值，根据模拟数据输出频率决定；n为模拟时长；式(3)中，nsei为水动力评价因子纳什效率系数。

计算结果见表3。

表3

a2.以选取的模型水质模拟精度评价因子为输出目标，计算各点位水质评价因子的相对误差、决定系数、纳什效率系数，计算公式如下：

式(1’)中，g为水质评价因子；reg为水质评价因子相对误差；mga为水质评价因子模拟平均值；sga为水质评价因子实测平均值；式(2’)中，rg²为水质评价因子决定系数；mgj为水质评价因子第j分钟(秒或小时)模拟值；sgj为水质评价因子第j分钟(秒或小时)实测值，根据模拟数据输出频率决定；n为模拟时长；式(3’)中，nseg为水质评价因子纳什效率系数。

计算结果见表4。

表4

a3.计算模型水动力模拟精度的平均相对误差、平均决定系数、平均纳什效率系数，计算公式如下：

式(4)中，i为水动力评价因子；k为评价点位；m为评价点位个数；reik为评价点位k上水动力评价因子i的相对误差；reia为水动力评价因子i的平均相对误差；式(5)中，rik²为评价点位k上水动力评价因子i的决定系数；ria²为水动力评价因子i的平均决定系数；式(6)中，nseik为评价点位k上水动力评价因子i的纳什效率系数；nseia为水动力评价因子i的平均纳什效率系数；式(7)中，rea为水动力模拟平均相对误差；h为水动力评价因子个数；式(8)中，ra²为水动力模拟平均决定系数；式(9)中，nsea为水动力模拟平均纳什效率系数。

计算结果见表5。

a4.计算模型水质模拟精度的平均相对误差、平均决定系数、平均纳什效率系数，计算公式如下：

式(4’)中，g为水质评价因子；k为评价点位；m为评价点位个数；regk为评价点位k上水质评价因子g的相对误差；rega为水质评价因子g的平均相对误差；式(5’)中，rgk²为评价点位k上水质评价因子g的决定系数；rga²为水质评价因子g的平均决定系数；式(6’)中，nsegk为评价点位k上水质评价因子g的纳什效率系数；nsega为水质评价因子g的平均纳什效率系数；式(7’)中，rea’为水质模拟平均相对误差；z为水质评价因子个数；式(8’)中，ra’²为水质模拟平均决定系数；式(9’)中，nsea’为水质模拟平均纳什效率系数。

计算结果见表5。

表5

a5.根据模型水动力模拟和水质模拟平均相对误差、平均决定系数和平均纳什效率系数的计算结果，对水环境数学模型模拟精度进行综合评价分析。

根据步骤a3和a4中模型水动力模拟和水质模拟平均相对误差、平均决定系数和平均纳什效率系数的计算结果可知：模型水动力模拟精度平均相对误差为18.2％，在20％以内，平均决定系数为0.49，小于0.6，平均纳什效率系数为0.349，小于0.6，平均决定系数、平均纳什效率系数均不满足要求，故模型水动力模拟不满足精度要求；模型水质模拟精度平均相对误差为1.15％，在20％以内，平均决定系数为0.75，大于0.6，平均纳什效率系数为0.771，大于0.6，平均相对误差、平均决定系数、平均纳什效率系数均满足要求，故模型水质模拟满足精度要求。

以上已以较佳实施例公布了本发明，然其并非用以限制本发明，凡采取等同替换或等效变换的方案所获得的技术方案，均落在本发明的保护范围内。