一种考虑源荷时序相关性的光伏消纳容量计算方法及装置与流程

本发明属于配电网光伏消纳技术领域，具体涉及一种考虑源荷时序相关性的光伏消纳容量计算方法及装置。

背景技术：

近年来，随着配电网光伏渗透率的逐渐上升，对于高渗透率下光伏消纳能力的研究也日趋深入。一方面，通过建立不同标准的数学评估模型研究网架的光伏消纳能力：比如利用潮流传输通道潮流熵建立网架评估模型或者建立考虑oid控制策略的配电网最大光伏电源有效接纳量评估模型，但缺乏对于光伏出力特性、负荷特性的分析，没有考虑两者时序相关性给电网带来的冲击；另一方面，通过多种方式简化模拟光伏的出力特性与典型场景，降低算法的维度，比如]采用超立方抽样处理新能源出力与负荷的相关性，或者通过序列化的方法、基于电压灵敏度的随机场景模拟法、蒙特卡洛随机法模拟描述含分布式电源的配电网系统的随机变化情况，并结合线路状态转移模型，对网架潮流进行风险评估。

综上，目前配电网光伏消纳能力分析还存在着两点不足。一是没有考虑到光伏出力的季节特性与当地负荷特性，电网实际的消纳能力应该将季节与时序特性涵盖进来，从而更加贴近电网的实际消纳能力；二是没有考虑实际配电网运行方式。目前，配电网的运行控制日趋网格化，网格化的运行控制以110kv公用变电站为核心对区域负荷实现切割，一个区域内按照负荷的水平由一至两个变电站为电源点，向下级配电网辐射供电。在单个配电网网格内，网格的主变升压容量、负荷水平与线路潮流限额数据清楚，网架简单同时潮流流向单一，光伏消纳能力的分析应以网格化为基础，分层分析区域的消纳能力，从而大幅度降低潮流计算维度，提高运算速度。

技术实现要素：

本发明的目的在于克服现有技术中的不足，提供了一种考虑源荷时序相关性的光伏消纳容量计算方法及装置，解决现有技术中因没有考虑光伏出力与地区负荷的相关性导致的光伏消纳能力评估偏差以及大规模电网光伏消纳能力计算维度高等技术问题。

为解决上述技术问题，本发明提供了一种考虑源荷时序相关性的光伏消纳容量计算方法，其特征是，包括以下过程：

获取各季节的典型负荷水平；

考虑源荷时序相关性，获取各季节在各个光伏典型场景下的光伏出力；

根据各季节的典型负荷水平和各季节的各个光伏典型场景下的光伏出力，结合预设的评估网格内最大消纳容量目标函数，计算得到各季节所对应的光伏最大消纳容量；

选取各季节所对应的光伏最大消纳容量中的最小值作为一年四季内光伏最大消纳容量。

进一步的，所述根据各季节的典型负荷水平和各季节的各个光伏典型场景下的光伏出力，结合预设的评估网格内最大消纳容量目标函数，计算得到各季节所对应的光伏最大消纳容量，包括：

针对某一季节，选取某一时刻的典型负荷水平以及该时刻下某一光伏典型场景下的光伏出力，在以上两个约束条件下，结合预设的评估网格内最大消纳容量目标函数，计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量；

针对各光伏典型场景下该时刻下的光伏出力，重复上一步过程，计算得到该季节在各个光伏典型场景下此时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节在此时刻的光伏最大消纳容量；

针对典型负荷水平内各个时刻，重复上一步过程，计算得到该季节各个时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节全天光伏最大消纳容量；

针对一年四季，重复以上所有过程，计算得到各季节所对应的光伏最大消纳容量。

进一步的，所述获取各季节的典型负荷水平具体包括以下过程：

1)对某一季节的日负荷数据进行聚类得到各个聚类中心序列；

2)选取日平均负荷率最低的聚类中心序列作为该季节的典型负荷水平。

进一步的，所述对某一季节的日负荷数据进行聚类得到各个聚类中心序列包括，对某一季节的日负荷数据进行dmk-means聚类得到各个聚类中心序列。

进一步的，所述对某一季节的日负荷数据进行dmk-means聚类得到各个聚类中心序列，具体包括以下过程：

11)对日负荷数据中的每一个日负荷时序序列，计算其最近邻集合；

12)计算每一个日负荷时序序列对应的最近邻集合的密度函数值；

13)从日负荷数据中删除密度值小于平均密度值的日负荷时序序列，剩余的日负荷时序序列形成新的密集数据矩阵；

14)对密集数据矩阵中各个日负荷时序序列进行聚类，得到各个聚类中心序列。

进一步的，所述考虑源荷时序相关性，获取各季节的各个光伏典型场景下的光伏出力，具体包括以下过程：

1)以全年为维度，将全年的光伏数据划分为四个维度：春、夏、秋、冬；

设第i季节的光伏数据矩阵为pvi＝[pvi,1,pvi,2,…,pvi,m,…,pvi,m]^t，其中为第i季节第m天的光伏出力序列，为第i个季节的第m天的d时刻光伏出力数据；

2)对于第i季节的典型日负荷时序序列和某一光伏出力序列pvi,m，将其转换成斜率时序序列c′i与pv′i,m，即：

式中，δt＝ttotal/d，ttotal为一天总时长；

3)采用时间序列的模式来描述时间序列的变化趋势，将斜率时序序列c′i与pv′i,m依据模式的评估标准，形成模式序列hci与hpvi,m，即：

式中，以及的评估过程如下：

式中，为转换成斜率组成的典型负荷时间序列的值，εcl、εcm、εch分别为负荷低增长、中增长、高增长的变化阈值；

式中，为转换成斜率组成的光伏出力时间序列的值，εvl、εvm、εvh分别为光伏出力低增长、中增长、高增长的变化阈值；

4)因此光伏出力序列pvi,m与典型日负荷时序序列ci的时序斜率距离为：

式中，kd为分段斜率距离，其计算公式为：

5)利用式(11)时序斜率距离来修正传统的欧式距离，即对于光伏出力序列pvi,m、pvi,n，其考虑源荷时序相关性的欧式距离公式为：

式中，λt是源荷时序相关性的权重系数；

6)利用式(13)考虑源荷时序相关性的欧式距离公式，采用dmk-means算法对某一季节的光伏出力序列进行聚类；筛选出不同光伏典型场景相对应的光伏典型出力时序序列代表不同光伏典型场景，指第i个季节第个光伏典型场景第d时刻的光伏出力值，d为一天的总时间。

进一步的，所述计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量包括，采用模拟退火粒子群算法计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量。

相应的，本发明还提供了一种考虑源荷时序相关性的光伏消纳容量计算装置，其特征是，包括获取典型负荷水平模块、获取光伏出力模块、计算单季光伏消纳容量模块和计算全年光伏消纳容量模块，其中：

第一计算模块、第二计算模块、第三计算模块和第四计算模块；其中：

获取典型负荷水平模块，用于获取各季节的典型负荷水平；

获取光伏出力模块，用于考虑源荷时序相关性，获取各季节在各个光伏典型场景下的光伏出力；

计算单季光伏消纳容量模块，用于根据各季节的典型负荷水平和各季节的各个光伏典型场景下的光伏出力，结合预设的评估网格内最大消纳容量目标函数，计算得到各季节所对应的光伏最大消纳容量；

计算全年光伏消纳容量模块，用于选取各季节所对应的光伏最大消纳容量中的最小值作为一年四季内光伏最大消纳容量。

7.根据权利要求6所述的一种考虑源荷时序相关性的光伏消纳容量计算装置，其特征是，计算单季光伏消纳容量模块中，所述根据各季节的典型负荷水平和各季节的各个光伏典型场景下的光伏出力，结合预设的评估网格内最大消纳容量目标函数，计算得到各季节所对应的光伏最大消纳容量，包括：

针对某一季节，选取某一时刻的典型负荷水平以及该时刻下某一光伏典型场景下的光伏出力作为约束条件，结合预设的评估网格内最大消纳容量目标函数，计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量；

针对各光伏典型场景下该时刻下的光伏出力，重复上一步过程，计算得到该季节在各个光伏典型场景下此时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节在此时刻的光伏最大消纳容量；

针对典型负荷水平内各个时刻，重复上一步过程，计算得到该季节各个时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节全天光伏最大消纳容量；

针对一年四季，重复以上所有过程，计算得到各季节所对应的光伏最大消纳容量。

进一步的，所述获取典型负荷水平模块中，获取各季节的典型负荷水平具体包括以下过程：

对某一季节的日负荷数据进行聚类得到各个聚类中心序列；

选取日平均负荷率最低的聚类中心序列作为该季节的典型负荷水平。

进一步的，所述获取典型负荷水平模块中对某一季节的日负荷数据进行聚类得到各个聚类中心序列包括，对某一季节的日负荷数据进行dmk-means聚类得到各个聚类中心序列。

进一步的，所述获取典型负荷水平模块中对某一季节的日负荷数据进行dmk-means聚类得到各个聚类中心序列，具体包括以下过程：

11)对日负荷数据中的每一个日负荷时序序列，计算其最近邻集合；

12)计算每一个日负荷时序序列对应的最近邻集合的密度函数值；

13)从日负荷数据中删除密度值小于平均密度值的日负荷时序序列，剩余的日负荷时序序列形成新的密集数据矩阵；

14)对密集数据矩阵中各个日负荷时序序列进行聚类，得到各个聚类中心序列。

进一步的，所述获取光伏出力模块中，考虑源荷时序相关性获取各季节的各个光伏典型场景下的光伏出力，具体包括以下过程：

1)以全年为维度，将全年的光伏数据划分为四个维度：春、夏、秋、冬；

设第i季节的光伏数据矩阵为pvi＝[pvi,1,pvi,2,…,pvi,m,…,pvi,m]^t，其中为第i季节第m天的光伏出力序列，为第i个季节的第m天的d时刻光伏出力数据；

2)对于第i季节的典型日负荷时序序列和某一光伏出力序列pvi,m，将其转换成斜率时序序列c′i与pv′i,m，即：

式中，δt＝ttotal/d，ttotal为一天总时长；

3)采用时间序列的模式来描述时间序列的变化趋势，将斜率时序序列ci'与pv′i,m依据模式的评估标准，形成模式序列hci与hpvi,m，即：

式中，以及的评估过程如下：

式中，为转换成斜率组成的典型负荷时间序列的值，εcl、εcm、εch分别为负荷低增长、中增长、高增长的变化阈值；

式中，为转换成斜率组成的光伏出力时间序列的值，εvl、εvm、εvh分别为光伏出力低增长、中增长、高增长的变化阈值；

4)因此光伏出力序列pvi,m与典型日负荷时序序列ci的时序斜率距离为：

式中，kd为分段斜率距离，其计算公式为：

5)利用式(11)时序斜率距离来修正传统的欧式距离，即对于光伏出力序列pvi,m、pvi,n，其考虑源荷时序相关性的欧式距离公式为：

式中，λt是源荷时序相关性的权重系数；

6)利用式(13)考虑源荷时序相关性的欧式距离公式，采用dmk-means算法对某一季节的光伏出力序列进行聚类；筛选出不同光伏典型场景相对应的光伏典型出力时序序列代表不同光伏典型场景，指第i个季节第个光伏典型场景第d时刻的光伏出力值，d为一天的总时间。

进一步的，所述第一计算模块中计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量包括，采用模拟退火粒子群算法计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量。

与现有技术相比，本发明所达到的有益效果是：本发明提供的一种考虑源荷时序相关性的光伏消纳容量计算方法，可以快速地计算出地区配电网的剩余光伏消纳容量。当前随着光伏产业的迅猛发展，地方政府、供电公司在发展光伏产业时应基于电网现有的容量合理有效地规划剩余可开发利用的容量空间，本方法基于实际网架，能够快速的给出当地电网可接入的极限光伏消纳容量，为决策单位作出光伏建设规划决策提供关键性支撑依据。

附图说明

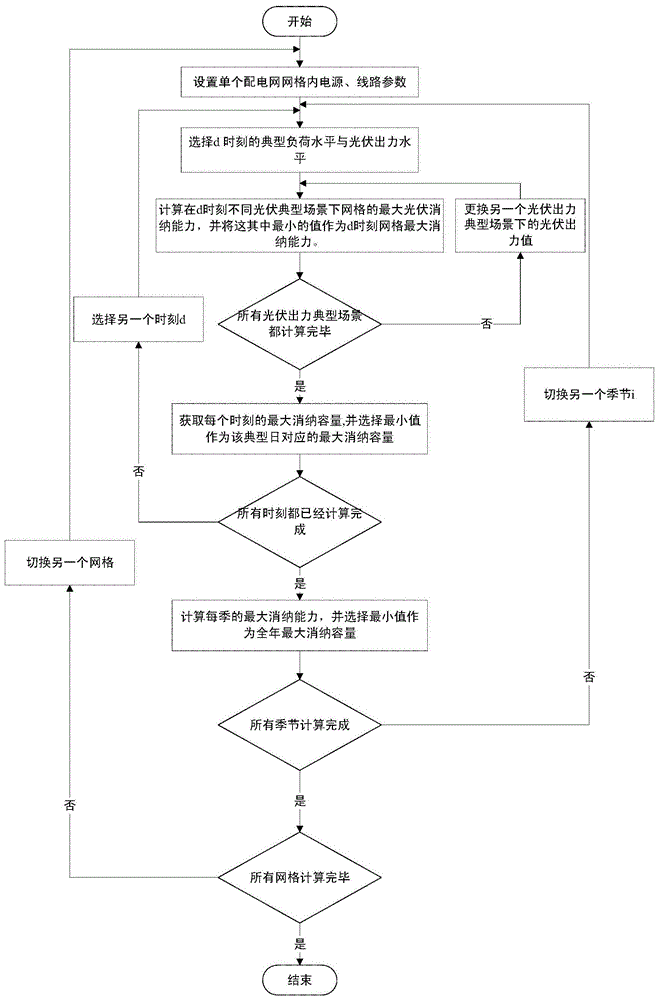
图1为本发明方法总体流程图；

图2为某区域配电网网格划分图；

图3为某网格网架结构图；

图4为四季典型负荷曲线图；

图5为典型光伏出力场景筛选曲线图；

图6为春季不同光伏出力场景下的接入容量曲线；

图7为四季网格最大接入光伏容量曲线图。

具体实施方式

下面结合附图对本发明作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

现有的配电网网架通常会划分成多个网格，该网格划分通常依据供电公司提供的运行方式对网格进行划分，保证每个网格由一个或两个220kv变电站供电，网格与网格间保持联络线联络，但通常为馈供网络。在计算光伏消纳容量时先针对单个配电网网格进行计算，则整个配电网区域的光伏极限消纳容量为单个网格消纳量的累加之和。

本发明的一种考虑源荷时序相关性的光伏消纳容量计算方法，包括以下过程：

s1，获取各季节的典型负荷水平；

s2，考虑源荷时序相关性，获取各季节在各个光伏典型场景下的光伏出力；

s3，针对某一季节，选取某一时刻的典型负荷水平以及该时刻下某一光伏典型场景下的光伏出力，在以上两个约束条件下，计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量；

s4，针对各光伏典型场景下该时刻下的光伏出力，重复步骤s3，计算得到该季节在各个光伏典型场景下此时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节在此时刻的光伏最大消纳容量；

s5，针对典型负荷水平内各个时刻，重复步骤s4，计算得到该季节各个时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节全天光伏最大消纳容量；

s6，针对一年四季，重复步骤s3～s5，计算得到各季节所对应的光伏最大消纳容量，选取其中的最小值作为一年四季内光伏最大消纳容量。

利用已有的地区全年的光伏出力与负荷波动曲线，利用考虑“源-荷”时序相关性的聚类方法，筛选出典型负荷水平下的多个光伏出力场景；并基于现有配电网区域的单元网格规划，对单个网格采用模拟退火粒子群优化算法计算可接入的光伏容量，并进一步获取单个网格极限消纳容量与整个配电网区域网格极限消纳容量。

实施例1

本发明的一种考虑源荷时序相关性的光伏消纳容量计算方法，参见图1所示，描述的是针对配电网的单个网格进行计算光伏消纳容量的详细步骤，具体包括以下步骤：

步骤一：从历史负荷数据中获取各季节的典型日负荷时序序列(负荷水平)。

首先获取单个网格的历史日负荷数据，以全年四季为维度，将全年的负荷数据划分为四个维度：春、夏、秋、冬。

设其中某一季节的日负荷数据矩阵为μi＝[μi,1,μi,2,…,μi,m,…,μi,m]^t，其中，i＝1,2,3,4代表一年四季，m为一季的总天数，为第i个季第m天的日负荷时序序列，在以下描述中可简称为序列或时序序列，为第i个季节第m天的d时刻负荷数据，d为负荷时序序列的一天的总时间(例如为早8点到晚10点的总时间)。

四个季节的典型日负荷时序序列(负荷水平)计算过程是一样的，下面以某一个季节为例来详细描述从单个季节的历史负荷数据中获取此季节的典型日负荷时序序列(负荷水平)的详细过程，具体包括以下步骤：

1)对第i季节的日负荷数据矩阵μi进行dmk-means聚类，得到聚类数量及各个聚类中心序列。

dmk-means聚类(densitymathematicskmeans，密度数据k均值聚类方法)是基于数据挖掘的k均值聚类方法，聚类的依据就是采用数据与数据之间的欧式距离来聚类。

对某一季的日负荷数据矩阵μi进行dmk-means聚类，具体的聚类过程为：

11)对日负荷数据矩阵μi中的每一个日负荷时序序列μi,m，计算其在给定邻域半径δ的最近邻集合nm为在μi,m邻域范围内的相邻日负荷时序序列数，邻域半径δ为经验值。

最近邻集合的计算过程为：将满足d(μi,m,μi,n)≤δ且μi,n∈μi条件的日负荷时序序列μi,n放入最近邻集合中，d(μi,m,μi,n)为日负荷时序序列μi,m、μi,n间的欧式距离，即：

12)计算每一个日负荷时序序列μi,m的密度函数值density(μi,m)，密度函数采用高斯函数，即：

式中，e为高斯函数，nm为最近邻集合中日负荷时序序列数，μi,ζ为最近邻集合中的某一日负荷时序序列(泛指)。

13)从日负荷数据矩阵μi中删除密度值小于平均密度值的日负荷时序序列，剩余的日负荷时序序列形成新的密集数据矩阵μi'。为了便于后续聚类，将密集数据矩阵μi'中各日负荷时序序列按密度值大小升序排列。

即对日负荷数据矩阵μi中的某一日负荷时序序列μi,m，判断是否满足以下条件：

式中，μi,ζ为最近邻集合中的某一日负荷时序序列(泛指)。

将满足上述条件的日负荷时序序列μi,m视为稀疏时序序列并从日负荷数据矩阵μi中剔除。判断完所有日负荷时序序列，从而得到一个排除了稀疏时序序列的密集数据矩阵μi'。

14)从密集数据矩阵μi'中，选取密度值最大的日负荷时序序列作为第一个初始聚类中心时序序列c1；然后从密度数据矩阵μi'中取距离c1最远的时序序列作为第二个初始聚类中心时序序列c2；对于第j个初始聚类中心序列cj的选取则是满足如下条件的序列：μi,j∈μ′i，i代表第i个季节，j代表第j个初始聚类中心，且该序列满足与目前已有的聚类中心序列的欧式距离之和最小的条件，即min(d(μi,j,c1)+d(μi,j,c2)+…+d(μi,j,cj-1))，则将序列μi,j作为第j个初始聚类中心序列为第i个季节第j个初始聚类中心序列第d时刻的值，直到得到最终所需的k个初始聚类中心序列，并代表k个聚类簇(k为预先设定的经验值)。

15)计算密集数据矩阵μi'中各个日负荷时序序列μi,m至各个初始聚类中心序列cj(j＝1,2,…,k)的欧式距离，计算公式为：

其中，为第i个季节第j个初始聚类中心序列第d时刻的值。

如果日负荷时序序列μi,m到第j个初始聚类中心序列cj的欧式距离为最小的距离值，则将该日负荷时序序列μi,m归于聚类中心cj所代表的聚类簇中，聚类中心cj所代表的聚类簇中时序序列的总数设为nj。当有新的日负荷时序序列加入聚类中心cj所代表的聚类簇中时，需要对聚类中心加以更新，聚类中心更新的方式是取这个聚类簇中所有日负荷时序序列值的平均值，即

式中，nj代表该聚类簇中的序列总数，代表第i个季节第j个聚类簇中第τ个时序序列中第d个时刻的值。

重复该过程直至最终聚类完成，得到k个聚类簇及各个聚类中心序列cj(j＝1,2,…,k)，每个聚类簇中有一个或者多个时序序列。

2)为了便于计算出配电网单个网格光伏消纳的最大能力，在k个聚类中心序列中选取日平均负荷率最低的聚类中心序列作为该i季节的典型日负荷时序序列

聚类中心序列cj的日平均负荷率的计算公式为：

式中，umean(cj)为聚类中心序列cj的日平均负荷率，j＝1,2,…,k，k为聚类簇总数；为第i个季节的第j个聚类中心序列的d时刻负荷数据，d为一天的总时间。

步骤二，考虑源荷时序相关性，从历史光伏数据中获取各季节的各个光伏典型场景下的光伏出力(其中，i代表与负荷划分相同的第i个季节，代表第个光伏典型场景，光伏典型场景指的是在不同天气条件下光伏出力呈现出的不同的光伏出力时序序列，不同天气下光伏的出力时序序列差异很大，因此把不同天气下光伏出力的典型时序序列作为光伏典型场景下的时序序列)。

四个季节的光伏出力计算过程是一样的，下面以某一个季节为例，来详细描述从某一季节的光伏数据中获取此季节的各个光伏典型场景下的光伏出力的详细过程，具体包括以下步骤：

1)与负荷曲线的划分相对应，以全年四季为维度，将全年的光伏数据划分为四个维度：春、夏、秋、冬。

设其中某一季的光伏数据矩阵为pvi＝[pvi,1,pvi,2,…,pvi,m,…,pvi,m]^t，i＝1,2,3,4代表一年四季，m为一季的总天数，其中为第i个季节第m天的光伏出力序列，为第i个季节的第m天的d时刻光伏出力数据。

2)对于上一步获得的第i个季节的典型日负荷时序序列和某一光伏出力序列pvi,m，将其转换成斜率时序序列c′i与pv′i,m，即：

式中，δt＝ttotal/d，ttotal为一天总时长。

3)采用时间序列的模式来描述时间序列的变化趋势，定义模式h＝{-3，-2，-1,0,1,2,3}分别用以表示{快速下降，保持下降，平稳下降，水平，缓慢上升，保持上升，快速上升}。将斜率时序序列ci'与pvi,'m依据模式h的评估标准，形成模式序列hci与hpvi,m，即：

式中，以及的评估过程如下：

式中，为转换成斜率组成的典型负荷时间序列的值，εcl、εcm、εch分别为负荷低增长、中增长、高增长的变化阈值。

式中，为转换成斜率组成的光伏出力时间序列的值，εvl、εvm、εvh分别为光伏出力低增长、中增长、高增长的变化阈值。

4)因此光伏出力序列pvi,m与典型日负荷时序序列ci的时序斜率距离为：

式中，kd为分段斜率距离，其计算公式为：

5)利用式(11)时序斜率距离来修正传统的欧式距离，即对于光伏出力序列pvi,m、pvi,n，其考虑源荷时序相关性的欧式距离公式为：

式中，λt是源荷时序相关性的权重系数。源指的是光伏出力，是电源；荷是负荷。这里的时序相关性就是利用光伏和负荷的变化趋势来聚类，所以叫源荷时序相关性。

6)利用式(13)考虑源荷时序相关性的欧式距离公式替代式(1)和式(4)的欧式距离，采用步骤一所述的dmk-means算法对某一季节的光伏出力序列进行聚类；并且由于光伏出力受天气影响，光伏有晴天、多云、突变等不同的典型场景，利用聚类筛选，不同天气的曲线会自动聚类成不同类，在曲线图中很明显能看出来。

利用聚类筛选出光伏典型场景，以及与不同光伏典型场景相对应的光伏典型出力时序序列(i＝1,2,3,4代表一年四季，代表不同光伏典型场景，例如晴天、多云、突变天气，指第i个季节第个光伏典型场景第d时刻的光伏出力值，d为一天的总时间)，聚类过程在此不再赘述。

步骤三，利用sa-pso(模拟退火粒子群)算法，在该光伏出力以及负荷水平的约束条件下，结合预设的评估网格内最大消纳容量目标函数，计算出该光伏出力以及负荷水平所对应的光伏最大消纳容量

详细步骤为：

1)评估网格内最大消纳容量的目标函数为：

式中，xl为网格内第l个节点接入的光伏总容量，n为网格内节点总数(含上级电源点)。

该目标函数的约束条件如下：

式中，ps、pl、pload、ploss分别代表网格内电源点供电有功出力(就是光伏出力)、第l个节点的光伏出力，总负荷(就是负荷水平)和总网损；vl为第l个节点的电压值；vlmin和vlmax分别为第l个节点的最小允许电压值和最大允许电压值；ij为第j条线路的电流值，ijmax为第j条线路的最大热稳定电流限值；pst代表网格内变电站主变升压或者降压的有功功率值，pst＞0代表变电站主变降压，pst＜0代表变电站主变升压倒送，smax为该变电站主变容量，为主变功率因数。

2)采用模拟退火粒子群算法(sa-pso)求解网格内光伏最大消纳容量。

21)初始化

设置粒子数为n，则对于第l个节点初始生成光伏接入容量的数组[xl,1,xl,2,…,xl,ξ,…,xl,n]^t，式中，xl,ξ代表第l个节点的第ξ个光伏接入容量值。容量就是每个光伏接入点需要接入多大的光伏；这个值一开始是初始值，是随机的；后续会通过sa-pso算出这个值；容量乘以典型光伏出力曲线就是光伏出力。

对整个区域，形成一个配电网网格的光伏接入容量方案的矩阵，如下：

式中，gξ(x)为初始状态下整个网格第ξ个光伏接入方案。

针对全天的某一时刻d，获取某一季节该时刻的典型负荷水平选取某一季节某一光伏典型场景下该时刻的的光伏出力对n个光伏接入方案进行潮流计算，获得目标函数所对应的全局最优光伏接入初始方案：

gbest-ini(x)＝[xbest-ini,1,…,xbest-ini,l,…,xbest-ini,n-1](17)

式中，xbest-ini,l表示第l个节点的全局最优光伏接入容量初始值。

22)依据初始方案和下述的更新公式对网格内的光伏接入容量方案矩阵{g1[x(m)],…,gξ[x(m)],…,gn[x(m)]}^t进行更新，该式中，gξ[x(m)]代表第m次迭代过程整个网格第ξ个的光伏接入方案，该矩阵如下：

式中，代表第m次迭代过程中第l个节点第ξ个光伏接入容量。

设xl,ξ(m)和vl,ξ(m)为第m次迭代时第l个节点可接入的第ξ个光伏容量值以及其变化量，则第l个节点的光伏容量值及其变化量的更新公式可表示为：

vl,ξ(m+1)＝χ[vl,ξ(m)+c1r1(xbest,l(m)-xl,ξ(m))+c2r2(xbest,l(m)-xl,ξ(m))](19)

xl,ξ(m+1)＝xl,ξ(m)+vl,ξ(m+1)(20)

式中，m为当前的迭代次数；c1、c2为加速常数；r1、r2为0～1均匀分布的随机数；xbest,l(m)为第m次迭代时刻的全局最优方案gbest[x(m)]中第l个节点接入的光伏容量(gbest[x(m)]＝[xbest,1(m),…,xbest,l(m),…,xbest,n-1(m)])；xbest,l(m)为全局最优方案gbest中第l个节点接入的光伏容量(gbest＝[xbest,1(m),…,xbest,l(m),…,xbest,n-1(m)])；χ为压缩因子，取决于加速常数，其计算公式为：

若发现第m次迭代后的区域最优方案gbest[x(m)]所对应的目标函数值大于全局最优方案gbest对应的目标函数值，则将全局最优方案替代为：gbest＝gbest[x(m)]。

23)重复步骤22)，依据xl,ξ(m)和vl,ξ(m)的更新公式进行迭代计算，获得gbest[x(m)]，并与gbest比较，不断更新全局最优方案。若迭代达到最大次数(例如10次)，全局最优方案均未发生变化或者超过迭代次数上限，退出迭代，输出全局最优的光伏接入方案gbest。

3)该网格针对第i季节d时刻的负荷水平以及第i季节第光伏典型场景下d时刻的光伏出力求解到的第i季节第光伏典型场景下d时刻的最大光伏消纳容量为：

式中，表示第l个节点依据第i个季节的第个典型场景下第d个时刻的光伏出力序列值以及第i个季节的第d时刻典型负荷时序序列值的条件下迭代获得的最大光伏消纳容量。n代表一个配电网网格内的节点数。

步骤四：对于第i季节各个光伏典型场景的光伏出力，重复上述步骤三，求解得到在不同光伏典型场景下d时刻所对应的光伏最大消纳容量，选取其中的最小值作为第i季节d时刻的光伏最大消纳容量

步骤五：光伏出力一般是从早6点至晚6点，对于第i季节典型日负荷时序序列内光伏出力不为零的各个时刻d，重复上述步骤四，从而获取了第i季节典型日负荷时序序列内各个时刻所对应的最大消纳容量，再从中选取最小值作为第i季节典型日负荷时序序列对应的该配电网网格的光伏最大消纳容量gi。

步骤六：对于一年四季，重复上述步骤三至五，计算得到四个季节的光伏最大消纳容量，取光伏消纳容量最小值作为一年四季内该网格光伏最大消纳容量，即gmin＝min(gi),i＝1,2,3,4。

计算出单个网格后，整个配电网区域的光伏最大消纳容量为每个网格光伏最大消纳容量之和。

实施例2

相应的，本发明还提供了一种考虑源荷时序相关性的光伏消纳容量计算装置，包括获取典型负荷水平模块、获取光伏出力模块、第一计算模块、第二计算模块、第三计算模块和第四计算模块；其中：

获取典型负荷水平模块，用于获取各季节的典型负荷水平；

获取光伏出力模块，用于考虑源荷时序相关性，获取各季节在各个光伏典型场景下的光伏出力；

第一计算模块，针对某一季节，选取某一时刻的典型负荷水平以及该时刻下某一光伏典型场景下的光伏出力，在以上两个约束条件下，结合预设的评估网格内最大消纳容量目标函数，计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量；

第二计算模块，针对各光伏典型场景下该时刻下的光伏出力，计算得到该季节在各个光伏典型场景下此时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节在此时刻的光伏最大消纳容量；

第三计算模块，针对典型负荷水平内各个时刻，计算得到该季节各个时刻所对应的光伏最大消纳容量，选取其中的最小值作为该季节全天光伏最大消纳容量；

第四计算模块，针对一年四季，计算得到各季节所对应的光伏最大消纳容量，选取其中的最小值作为一年四季内光伏最大消纳容量。

进一步的，所述获取典型负荷水平模块中，获取各季节的典型负荷水平具体包括以下过程：

1)对某一季节的日负荷数据进行聚类得到各个聚类中心序列；

2)选取日平均负荷率最低的聚类中心序列作为该季节的典型负荷水平。

进一步的，所述获取典型负荷水平模块中对某一季节的日负荷数据进行聚类得到各个聚类中心序列包括，对某一季节的日负荷数据进行dmk-means聚类得到各个聚类中心序列。

进一步的，所述获取典型负荷水平模块中对某一季节的日负荷数据进行dmk-means聚类得到各个聚类中心序列，具体包括以下过程：

11)对日负荷数据中的每一个日负荷时序序列，计算其最近邻集合；

12)计算每一个日负荷时序序列对应的最近邻集合的密度函数值；

13)从日负荷数据中删除密度值小于平均密度值的日负荷时序序列，剩余的日负荷时序序列形成新的密集数据矩阵；

14)对密集数据矩阵中各个日负荷时序序列进行聚类，得到各个聚类中心序列。

进一步的，所述获取光伏出力模块中，考虑源荷时序相关性获取各季节的各个光伏典型场景下的光伏出力，具体包括以下过程：

1)以全年为维度，将全年的光伏数据划分为四个维度：春、夏、秋、冬；

设第i季节的光伏数据矩阵为pvi＝[pvi,1,pvi,2,…,pvi,m,…,pvi,m]^t，其中为第i季节第m天的光伏出力序列，为第i个季节的第m天的d时刻光伏出力数据；

2)对于第i季节的典型日负荷时序序列和某一光伏出力序列pvi,m，将其转换成斜率时序序列c′i与pv′i,m，即：

式中，δt＝ttotal/d，ttotal为一天总时长；

3)采用时间序列的模式来描述时间序列的变化趋势，将斜率时序序列c′i与pv′i,m依据模式的评估标准，形成模式序列hci与hpvi,m，即：

式中，以及的评估过程如下：

式中，为转换成斜率组成的典型负荷时间序列的值，εcl、εcm、εch分别为负荷低增长、中增长、高增长的变化阈值；

式中，为转换成斜率组成的光伏出力时间序列的值，εvl、εvm、εvh分别为光伏出力低增长、中增长、高增长的变化阈值；

4)因此光伏出力序列pvi,m与典型日负荷时序序列ci的时序斜率距离为：

式中，kd为分段斜率距离，其计算公式为：

5)利用式(11)时序斜率距离来修正传统的欧式距离，即对于光伏出力序列pvi,m、pvi,n，其考虑源荷时序相关性的欧式距离公式为：

式中，λt是源荷时序相关性的权重系数；

6)利用式(13)考虑源荷时序相关性的欧式距离公式，采用dmk-means算法对某一季节的光伏出力序列进行聚类；筛选出不同光伏典型场景相对应的光伏典型出力时序序列代表不同光伏典型场景，指第i个季节第个光伏典型场景第d时刻的光伏出力值，d为一天的总时间。

进一步的，所述第一计算模块中计算得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量包括，采用模拟退火粒子群算法计算评估网格内最大消纳容量目标函数，得到该季节在此光伏典型场景下此时刻所对应的光伏最大消纳容量。

实施例3

本发明实施例以南通海安县实际电网验证本消纳预警评估方法的合理性。南通市海安地区的配电网已经采用网格化的分区管理方式，将整个地区划分为66个子网格，其中接入新能源的网格共有24个，需要评估全县的光伏消纳能力。南通海安县的网格化划分图如附图2所示。

以海安县110kv李堡变为例，其配电网网架以李堡变为中心，向四周呈辐射状分布，如附图3所示。该网格内配电网结构清晰，功率流向稳定，有效降低了配电网潮流计算的复杂度与计算量。

以南通市海安县2016年6月～2017年5月全年的负荷数据为基础，采用dmk-means算法对四季的典型负荷曲线进行聚类分析，获得的四季典型负荷水平如附图4所示。

基于附图4所示的四季典型负荷曲线，采用考虑源荷时序相关性的dmk-means聚类方法，对海安县各个季节的光伏出力场景进行筛选。以春季为例，取参数λt＝0.75，筛选出光伏在不同天气条件下的出力场景(不同的天气对应不同的典型出力场景)，如附图5所示。

图5显示了采用本申请中的考虑时序相关的dmk-means聚类与现有技术的k-means聚类筛选出的光伏在不同天气条件下的出力场景。从附图5中可以看出，考虑时序相关的dmk-means聚类由于引入了斜率距离，使得光伏出力曲线间的变化趋势能够互相匹配(指相同天气的光伏出力具备相似性，即相同天气的光伏出力相互匹配)，从而准确地分出代表晴天的c1以及代表多云的c2，具有较好的降噪效果；而k-means的聚类结果较为模糊，并不能有效区分c1与c2的不同特征。在c3突变天气上，由于突变天气的特征不明显，两类聚类均不能给出统一的模式，但是考虑时序相关的dmk-means聚类可以更好的匹配春季典型负荷曲线8时-12时的负荷波动，筛选出该时段与负荷曲线突变趋势相反的曲线，从而便于对网架的极限消纳能力进行更精确的校核。

以附图3中展示的网格为例，该网格中线路输送能力如表1所示。

表1李堡变网格情况表

李堡变的主变容量为31.5+63mva，尚海线接入光伏1mw，曹园线接入光伏5.5mw，依据附图4中的地区典型负荷曲线以及附图5中筛选出的光伏典型出力场景，对该网格的极限消纳能力进行计算，其在不同光伏出力场景下的春季最大消纳能力如附图6(a)所示，附图6(b)是由附图6(a)中多场景下的消纳能力曲线包络而成，从中可以获知该网格春季极限消纳能力为46.45mw。

进一步对四个季节的光伏消纳能力进行计算，获得的全年时序消纳能力如附图7所示。从附图7中可以看出，该网格的光伏极限消纳能力随着季节负荷水平以及光伏出力场景的变化而变化，最终计算得到的该网格全年极限消纳能力为46mw。

传统的光伏消纳能力估算通常为潮流通道(含线路与主变)的输送能力与网格最大负荷的迭加，依据此传统方法估算出本网格的全年极限消纳能力为55mw。然而这种粗略的估算并没有考虑到光伏出力的逆调峰特性，在负荷高峰时刻，光伏出力可能呈现突变(白天天气变化)或者零出力(夜间负荷高峰)的情况，使得光伏极限消纳能力的计算存在误差，导致光伏消纳预警等级的评估结果存在误判的可能。

与现有技术相比，本发明的有益效果为：

本发明将光伏出力的突变性与当地负荷特性综合考虑，充分考虑了光伏逆调峰可能给当地电网带来的潮流阻塞、主变升压过载的问题，从而在传统方法的基础上，进一步精确地计算出光伏极限消纳容量。同时，本文采用考虑源荷时序相关性的聚类方法，有效地提取出典型日负荷时序序列与典型光伏出力场景，有效地降低了数据维度，又保持了数据的典型特征，计算结果能够为当地光伏规划提供有效支撑。

本领域内的技术人员应明白，本申请的实施例可提供为方法、系统、或计算机程序产品。因此，本申请可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本申请可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。

本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。

这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。

这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。

以上所述仅是本发明的优选实施方式，应当指出，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变形，这些改进和变形也应视为本发明的保护范围。