基于多模态分布估计算法的卫星布局优化设计方法与流程

本发明涉及卫星设计技术领域，具体涉及一种基于多模态分布估计算法的卫星布局优化设计方法。

背景技术：

随着空间技术及产业化的迅速发展，卫星设计的要求越来越高；通常为了缩短卫星设计周期、降低研制成本、以及保证卫星设计的可靠性、标准化、系列化和通用化，要求在卫星确定有效载荷和公用平台后，对卫星上的组件进行合理的总体布局。

卫星组件的布局优化设计是卫星总体方案设计的重要内容，现有的卫星组件的布局优化设计方法通过建立一个单目标卫星布局优化设计模型，并设计相应的单目标布局优化算法来对该单目标卫星布局优化设计模型进行求解，以获得一组布局优化结果；工作人员基于获得的布局优化结果，依赖工程经验给出满足要求的一个或几个较优的卫星布局设计方案。但由于卫星布局设计方案利用工程经验给出，无法验证提出的卫星布局设计方案是否为最优方案；并且，现有的单目标布局优化设计算法主要包括梯度法和智能优化算法，但梯度法容易陷入局部最优，而大多数的智能优化算法只能求得一个可行解且无法保证得到的可行解是否为最优方案。

技术实现要素：

为解决上述现有技术中存在的技术问题，本发明提供一种基于多模态分布估计算法的卫星布局优化设计方法。

为此，本发明公开了一种基于多模态分布估计算法的卫星布局优化设计方法，所述方法包括如下内容：

(1)对卫星内部的结构和设备进行近似描述，建立卫星布局设计方案的简化结构模型；

(2)基于所述简化结构模型，确定设计约束和设计目标，建立单目标多约束的卫星布局优化设计模型；

(3)利用多模态分布估计算法对所述单目标多约束的卫星布局优化设计模型进行优化求解，以获取所述设计约束和所述设计目标下的卫星布局设计方案解集；

(4)根据获取的所述卫星布局设计方案解集，确定所述设计约束和所述设计目标下的所述卫星的最终布局方案。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述对卫星内部的结构和设备进行近似描述，建立卫星布局设计方案的简化结构模型，包括：

设定卫星舱外壳为圆柱体或立方体，设定卫星组件为圆柱体或立方体，以及设定所述卫星组件质量均匀分布且质心与形心重合；

设定所述卫星组件均安装在所述卫星舱内的承力板上，且不同所述承力板上的所述卫星组件无空间干涉；

基于上述设定，建立卫星布局的三维坐标系o-xyz，将所述承力板的中心作为坐标原点o，将所述承力板的安装面作为xoy面，并使z轴垂直于所述承力板的安装面向上，x轴、y轴和所述z轴构成右手直角坐标系。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述设计约束包括卫星系统质心误差和卫星系统惯性夹角误差，所述设计目标包括降低卫星整体的转动惯量。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述单目标多约束的卫星布局优化设计模型表述为：

其中，x表示卫星的布局方案，n表示卫星组件总数，(xi,yi)表示卫星组件i的位置坐标，f(x)表示对应卫星整体的转动惯量的目标函数，jx'表示卫星绕着x轴的转动惯量，jy'表示卫星绕着y轴的转动惯量，jz'表示卫星绕着z轴的转动惯量，g1(x)表示卫星组件之间的不干涉约束，δvij表示卫星组件i和卫星组件j之间的干涉量，g2(x)和g3(x)表示卫星系统质心约束，(xc,yc)表示卫星的真实质心坐标，(xe,ye)表示卫星的期望质心坐标，(δxe,δye)表示所允许的卫星的最大质心偏差，g4(x)、g5(x)和g6(x)表示卫星系统惯性夹角约束，(θx',θy',θz')表示卫星绕三个坐标轴方向的惯性夹角，(δθx',δθy',δθz')表示所允许的卫星绕三个坐标轴方向的最大惯性夹角。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述利用多模态分布估计算法对所述单目标多约束的卫星布局优化设计模型进行优化求解，以获取所述设计约束和所述设计目标下的卫星布局设计方案解集，包括：

(a1)根据卫星的设计约束和设计目标，确定目标函数；

(a2)基于目标函数，产生设定数目的卫星布局设计方案，并设置循环终止条件；

(a3)利用小生境算法将设定数目的卫星布局设计方案划分为多个小生境；

(a4)挑选出每个小生境中的当前最优方案，利用高斯分布估计算法进行采样迭代以获取每个小生境的一个最优方案；

(a5)在获取的每个小生境的一个最优方案处使用序列二次规划法进行局部寻优，获取并输出多个全局最优方案；

(a6)将获取的每个小生境的一个最优方案存入档案集中，若档案集不存在，设置一个初始为空集的档案集；

(a7)判断循环终止条件是否满足，若是，输出档案集，若否，进行下一步；

(a8)计算确定最优方案数目，基于目标函数，产生多个新卫星布局设计方案，且使新卫星布局设计方案的数目等于设定数目减去最优方案数目，将最优方案和新卫星布局设计方案作为卫星布局设计方案，返回步骤a3。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述利用小生境算法将设定数目的卫星布局设计方案划分为多个小生境，包括：

根据自适应半径划分小生境；

根据等数目原则进行小生境调整。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述根据自适应半径划分小生境，包括：

(b1)根据目标函数，计算确定设定数目的卫星布局设计方案对应的目标函数值；

(b2)根据卫星布局设计方案所对应的目标函数值对未划分小生境的卫星布局设计方案进行排序；

(b3)选择最小目标函数值对应的卫星布局设计方案作为聚类中心，根据其他剩余卫星布局设计方案与聚类中心的距离进行排序，依次比较相邻的两个卫星布局设计方案的目标函数值的大小，当大小关系出现变化时，以聚类中心和出现变化时对应的卫星布局设计方案间的距离作为小生境半径，将聚类中心和与聚类中心的距离小于小生境半径的所有卫星布局设计方案划分为一个小生境；

(b4)判断未划分小生境的卫星布局设计方案的数目是否为0，若是，进行步骤b5，若否，返回步骤b2；

(b5)输出获取的所有小生境。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述根据等数目原则进行小生境调整，包括：

(c1)确定每个小生境内的卫星布局设计方案个数；

(c2)根据卫星布局设计方案所对应的目标函数值对每个小生境内的卫星布局设计方案进行排序；

(c3)依次判断每个小生境内的卫星布局设计方案个数和设定数目与小生境数目的比值的关系，若卫星布局设计方案个数等于设定数目与小生境数目的比值，输出对应的小生境的全部卫星布局设计方案；若卫星布局设计方案个数大于设定数目与小生境数目的比值，输出对应的小生境中位于前序的部分卫星布局设计方案，且该部分卫星布局设计方案的数目等于设定数目与小生境数目的比值；若卫星布局设计方案个数小于设定数目与小生境数目的比值，利用目标函数产生卫星布局设计方案，且产生的卫星布局设计方案的数目等于设定数目与小生境数目的比值和对应的小生境内的卫星布局设计方案个数的差值，将产生的卫星布局设计方案添加到对应的小生境，输出对应的小生境的全部卫星布局设计方案。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，所述利用高斯分布估计算法进行采样迭代以获取每个小生境的一个最优方案，包括：

(d1)根据目标函数，设定终止条件；

(d2)根据设计空间范围，确定方案容量，设定初始采样概率密度函数的分布参数向量；

(d3)判断终止条件是否满足，若是，进行步骤d7；若否，进行下一步；

(d4)根据概率密度函数生成相互独立的卫星布局设计方案并计算卫星布局设计方案对应的目标函数值；

(d5)将目标函数值以从大到小的顺序进行排序；

(d6)利用一个小生境中的所有方案对分布参数向量进行更新，而后返回步骤d3；

(d7)结束循环，输出最小目标函数值对应的卫星布局设计方案。

进一步地，在上述基于多模态分布估计算法的卫星布局优化设计方法中，概率密度函数为高斯分布函数，概率密度函数的分布参数向量包括均值向量和方差向量，均值利用下述公式2进行计算更新，方差利用下述公式3和公式4进行计算更新；

其中，表示第i个小生境的第t个高斯分布的均值，表示第i个小生境的第t个高斯分布中目标函数值最小的方案，为第i个小生境的初始方差，α为控制系数，用于控制初始采样方案的分布空间，控制系数越大，初始采样越集中，ub(d)为第d维设计变量上限，lb(d)为第d维设计变量下限，d为设计变量的维数，d为维数参数，为第i个小生境的第t个高斯分布的方差，为第i个小生境的第t个高斯分布的所有方案，x为第i个小生境的第t个高斯分布的一个方案，为第i个小生境的第t个高斯分布的均值，为第i个小生境的第t个高斯分布的方案数目。

本发明技术方案的主要优点如下：

本发明的基于多模态分布估计算法的卫星布局优化设计方法通过利用基于小生境算法和高斯分布估计算法更新机制的多模态分布估计算法，并在多模态分布估计算法中应用序列二次规划法局部优化机制和交叉算子，能够实现卫星布局设计问题的优化求解，获得在设定设计约束和设计目标下的最优卫星布局设计方案，且能有效地降低求解工作量。

附图说明

为了更清楚地说明本发明实施例或现有技术中的技术方案，下面将对实施例或现有技术描述中所需要使用的附图作简单地介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。

图1为本发明一实施例的基于多模态分布估计算法的卫星布局优化设计方法的流程图；

图2为本发明一实施例的卫星布局设计方案的简化结构模型；

图3为本发明一实施例的多模态分布估计算法的流程图；

图4为本发明一实施例的自适应小生境半径的确定原理示意图。

具体实施方式

为使本发明的目的、技术方案和优点更加清楚，下面将结合本发明具体实施例及相应的附图对本发明技术方案进行清楚、完整地描述。显然，所描述的实施例仅是本发明的一部分实施例，而不是全部的实施例。基于本发明的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。

以下结合附图，详细说明本发明实施例提供的技术方案。

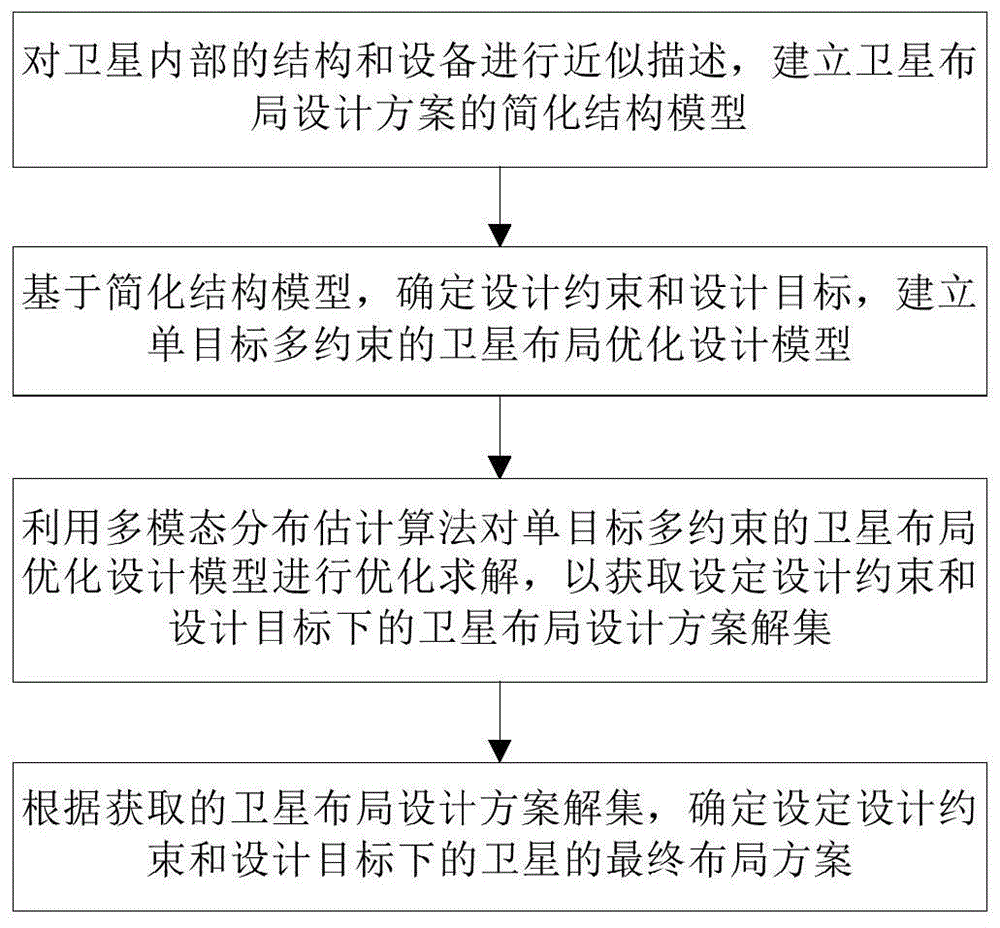
如附图1所示，本发明一实施例提供了一种基于多模态分布估计算法的卫星布局优化设计方法，该方法包括如下步骤：

(1)对卫星内部的结构和设备进行近似描述，建立卫星布局设计方案的简化结构模型；

(2)基于简化结构模型，确定设计约束和设计目标，建立单目标多约束的卫星布局优化设计模型；

(3)利用多模态分布估计算法对单目标多约束的卫星布局优化设计模型进行优化求解，以获取设定设计约束和设计目标下的卫星布局设计方案解集；

(4)根据获取的卫星布局设计方案解集，确定设定设计约束和设计目标下的卫星的最终布局方案。

以下对本发明一实施例提供的基于多模态分布估计算法的卫星布局优化设计方法的各个步骤及原理进行具体说明。

本发明一实施例中，基于现有的卫星的结构特点，如附图2所示，步骤1中对卫星内部的结构和设备进行近似描述，建立卫星布局设计方案的简化结构模型，可以采用如下方式进行：

设定卫星舱外壳为圆柱体或立方体，设定卫星组件为圆柱体或立方体，以及设定卫星组件质量均匀分布且质心与形心重合；

设定卫星组件均安装在卫星舱内的承力板上，且不同承力板上的卫星组件无空间干涉；

基于上述设定，建立卫星布局的三维坐标系o-xyz，将承力板的中心作为坐标原点o，将承力板的安装面作为xoy面，并使z轴垂直于承力板的安装面向上，x轴、y轴和z轴构成右手直角坐标系。

其中，每一个承力板建立一个相对应的三维坐标系。

如此设置，在进行卫星三维布局优化设计时，由于卫星组件只安装在某一个承力板上，在对该承力板上的卫星组件的布局进行研究，只需研究沿z轴方向进行投影后的二维平面布局优化问题，即可将卫星布局的三维布局优化设计问题转化为两个或多个二维平面内的矩形与圆的布局优化问题。

基于上述的卫星布局设计方案的简化结构模型，设计约束例如可以包括卫星系统质心误差和卫星系统惯性夹角误差，设计目标例如可以为降低卫星整体的转动惯量。当然，设计约束也可以为三个及以上，本发明一实施例将设计约束设定为两个，是用于对本发明一实施例提供的多目标卫星布局优化设计方法的具体步骤和原理进行示例说明，并不限定设计约束的个数；根据本发明一实施例具体提供的针对两个设计约束和一个设计目标的卫星布局优化设计方法，可以得出针对三个以上的设计约束的卫星布局优化设计方法。

在上述设定的两个设计约束和一个设计目标下，单目标多约束的卫星布局优化设计模型可表述为：

其中，x表示卫星的布局方案，n表示卫星组件总数，(xi,yi)表示卫星组件i的位置坐标，f(x)表示对应卫星整体的转动惯量的目标函数，jx'表示卫星绕着x轴的转动惯量，jy'表示卫星绕着y轴的转动惯量，jz'表示卫星绕着z轴的转动惯量，g1(x)表示卫星组件之间的不干涉约束，δvij表示卫星组件i和卫星组件j之间的干涉量，g2(x)和g3(x)表示卫星系统质心约束，(xc,yc)表示卫星的真实质心坐标，(xe,ye)表示卫星的期望质心坐标，(δxe,δye)表示所允许的卫星的最大质心偏差，g4(x)、g5(x)和g6(x)表示卫星系统惯性夹角约束，(θx',θy',θz')表示卫星绕三个坐标轴方向的惯性夹角，(δθx',δθy',δθz')表示所允许的卫星绕三个坐标轴方向的最大惯性夹角。

进一步地，基于上述设定的两个设计约束和一个设计目标，利用多模态分布估计算法对单目标两约束的卫星布局优化设计模型进行优化求解，以获取设定设计约束和设计目标下的卫星布局设计方案解集。

具体地，本发明一实施例中，利用多模态分布估计算法对单目标多约束的卫星布局优化设计模型进行优化求解，以获取设定设计约束和设计目标下的卫星布局设计方案解集，包括如下内容：

(a1)根据卫星的设计约束和设计目标，确定目标函数；

具体地，以设计约束为卫星系统质心误差和卫星系统惯性夹角误差，设计目标为降低卫星整体的转动惯量为例，目标函数则可表示为f(x)＝jx'(x)+jy'(x)+jz'(x)，f(x)表示对应卫星整体的转动惯量的目标函数，jx'表示卫星绕着x轴的转动惯量，jy'表示卫星绕着y轴的转动惯量，jz'表示卫星绕着z轴的转动惯量。

(a2)基于目标函数，产生设定数目的卫星布局设计方案，并设置循环终止条件；

具体地，设定数目可以根据具体设定的设计约束和设计目标进行确定，设计约束和设计目标越多，相对应的优化问题越复杂，则设定数目越多，在上述步骤a1确定的设定约束、设计目标和目标函数的基础上，设定数目例如可以设置为400；循环终止条件可以为迭代次数或者目标函数计算次数，迭代次数的具体值或者目标函数计算次数的具体值可以根据具体设定的设计约束和设计目标进行确定，在上述步骤a1确定的设定约束、设计目标和目标函数的基础上，循环终止条件例如可以为300次迭代次数或者40000次目标函数计算次数。

(a3)利用小生境算法将设定数目的卫星布局设计方案划分为多个小生境；

具体地，本发明一实施例中，利用小生境算法将设定数目的卫星布局设计方案划分为多个小生境，包括：根据自适应半径划分小生境；根据等数目原则进行小生境调整。

其中，根据自适应半径划分小生境可以包括如下内容：

(b1)根据目标函数，计算确定设定数目的卫星布局设计方案对应的目标函数值；

(b2)根据卫星布局设计方案所对应的目标函数值对未划分小生境的卫星布局设计方案进行排序；

(b3)选择最小目标函数值对应的卫星布局设计方案作为聚类中心，根据其他剩余卫星布局设计方案与聚类中心的距离进行排序，依次比较相邻的两个卫星布局设计方案的目标函数值的大小，当大小关系出现变化时，以聚类中心和出现变化时对应的卫星布局设计方案间的距离作为小生境半径，将聚类中心和与聚类中心的距离小于小生境半径的所有卫星布局设计方案划分为一个小生境；

(b4)判断未划分小生境的卫星布局设计方案的数目是否为0，若是，进行步骤b5，若否，返回步骤b2；

(b5)输出获取的所有小生境。

以下通过示例对本发明一实施例提供的根据自适应半径划分小生境的原理进行说明：

如附图2所示，假设：a、b、c和d是卫星布局设计方案，以求解目标函数最小值问题为例，x表示自变量，y表示函数值，a和c则分别代表最优卫星布局设计方案和最差卫星布局设计方案，由于a对应的函数值最小，a被确定为聚类中心，根据其他所有卫星布局设计方案与a的距离进行排序，依次比较两个卫星布局设计方案对应的函数值大小，当出现相邻卫星布局设计方案对应的函数值大小关系出现变化时，那么小生境半径则被确定，例如b对应的函数值小于c，而c对应的函数值大于d，此时a和c的距离r即确定为小生境半径。

进一步地，当采用根据自适应半径划分小生境的方式将卫星布局设计方案划分为多个小生境时，每个小生境中的卫星布局设计方案个数可能不完全一致，本发明一实施例中，为了保证获取的每个小生境中的卫星布局设计方案个数相同，在根据自适应半径划分小生境后，还根据等数目原则进行小生境调整。

具体地，根据等数目原则进行小生境调整可以包括如下内容：

(c1)确定每个小生境内的卫星布局设计方案个数；

(c2)根据卫星布局设计方案所对应的目标函数值对每个小生境内的卫星布局设计方案进行排序；

(c3)依次判断每个小生境内的卫星布局设计方案个数和设定数目与小生境数目的比值的关系，若卫星布局设计方案个数等于设定数目与小生境数目的比值，输出对应的小生境的全部卫星布局设计方案；若卫星布局设计方案个数大于设定数目与小生境数目的比值，输出对应的小生境中位于前序的部分卫星布局设计方案，且该部分卫星布局设计方案的数目等于设定数目与小生境数目的比值；若卫星布局设计方案个数小于设定数目与小生境数目的比值，利用目标函数产生卫星布局设计方案，且产生的卫星布局设计方案的数目等于设定数目与小生境数目的比值和对应的小生境内的卫星布局设计方案个数的差值，将产生的卫星布局设计方案添加到对应的小生境，输出对应的小生境的全部卫星布局设计方案。

如此，能够将根据目标函数产生的卫星布局设计方案划分为多个小生境，并保证划分后的每个小生境内的卫星布局设计方案的数目一致，以便后续处理。

(a4)挑选出每个小生境中的当前最优方案，利用高斯分布估计算法进行采样迭代以获取每个小生境的一个最优方案；

具体地，利用高斯分布估计算法进行采样迭代以获取每个小生境的一个最优方案，包括如下内容：

(d1)根据目标函数，设定终止条件；

(d2)根据设计空间范围，确定方案容量，设定初始采样概率密度函数的分布参数向量；

(d3)判断终止条件是否满足，若是，进行步骤d7；若否，进行下一步；

(d4)根据概率密度函数生成相互独立的卫星布局设计方案并计算卫星布局设计方案对应的目标函数值；

(d5)将目标函数值以从大到小的顺序进行排序；

(d6)利用一个小生境中的所有方案对分布参数向量进行更新，而后返回步骤d3；

(d7)结束循环，输出最小目标函数值对应的卫星布局设计方案。

其中，终止条件可以为迭代次数或者目标函数计算次数，迭代次数的具体值或者目标函数计算次数的具体值可以根据具体设定的设计约束和设计目标进行确定，在上述步骤a1确定的设定约束、设计目标和目标函数的基础上，终止条件例如可以为100次迭代次数或者20000次目标函数计算次数。

本发明一实施例中，概率密度函数为高斯分布函数，概率密度函数的分布参数向量包括均值向量和方差向量；在利用高斯分布估计算法进行采样迭代时，先根据目标函数和设计空间范围，确定一个初始中心点和初始标准差，即初始均值向量和初始方差向量，再利用初始中心点和初始标准差产生第一代方案；然后基于第一代方案，进行均值向量和方差向量的更新，再利用新的均值向量和方差向量产生下一代方案进行迭代计算，再利用新的一代方案进行均值向量和方差向量的更新；循环迭代，直到最终结果达到设定的终止条件。

传统分布估计算法中概率模型更新时，均值采用计算精英样本(方案)的均值，这种方法虽然具有较好的鲁棒性，但收敛速度慢，且精英样本比例对于均值更新有较大影响；本发明一实施例中，由于划分为小生境后，每个小生境覆盖的区域并不复杂，为此使用小生境中最优方案进行均值更新。

具体地，均值可以利用公式2进行更新；

式中，表示第i个小生境的第t个高斯分布的均值，表示第i个小生境的第t个高斯分布中目标函数值最小的方案。

进一步地，由于对于设计空间进行了划分，因此不需要对全空间进行采样，在已知上下界的情况下，本发明一实施例中，方差可以利用公式3和公式4进行更新；

式中，为第i个小生境的初始方差，α为控制系数，用于控制初始采样方案的分布空间，控制系数越大，初始采样越集中，ub(d)为第d维设计变量上限，lb(d)为第d维设计变量下限，d为设计变量的维数，d为维数参数，为第i个小生境的第t个高斯分布的方差，为第i个小生境的第t个高斯分布的所有方案，x为第i个小生境的第t个高斯分布的一个方案，为第i个小生境的第t个高斯分布的均值，为第i个小生境的第t个高斯分布的方案数目。

(a5)在获取的每个小生境的一个最优方案处使用序列二次规划法进行局部寻优，获取并输出多个全局最优方案；

具体地，在经过上述步骤a4的迭代之后，得到多个最优方案中每个方案基本接近最优解区域，但精度可能相对不高，为了进一步得到全局最优方案，通过在得到的多个最优方案的每个方案处使用序列二次规划法(sequentialquadraticprogramming，sqp)进行局部寻优，能够得到目标函数的多个全局最优解，以实现卫星布局优化目的。

(a6)将获取的每个小生境的一个最优方案存入档案集中，若档案集不存在，设置一个初始为空集的档案集；

(a7)判断循环终止条件是否满足，若是，输出档案集，若否，进行下一步；

(a8)计算确定最优方案数目，基于目标函数，产生多个新卫星布局设计方案，且使新卫星布局设计方案的数目等于设定数目减去最优方案数目，将最优方案和新卫星布局设计方案作为卫星布局设计方案，返回步骤a3。

具体地，为了提高迭代过程中的样本多样性，提高最终获取的全局最优解的精度，以得到在设定设计约束和设计目标下的最优卫星布局设计方案，多个新卫星布局设计方案可以利用不同小生境之间的交叉算子产生；

本发明一实施例中，可以利用公式5确定多个新卫星布局设计方案；

式中，表示通过交叉算子产生的新卫星布局设计方案，表示第j个小生境的最优方案，表示第k个小生境的最优方案，d表示设计变量的维数，d为维数参数，rand()表示随机数。

进一步地，在完成卫星布局设计方案的全局最优解的求解后，由于每一个全局最优解都是在设定设计约束和设计目标下的一个局部最优卫星布局设计方案，通过对获取的多个局部最优卫星布局设计方案进行比较，即可得到在设定设计约束和设计目标下的最优卫星布局设计方案。

可见，本发明一实施例提供的基于多模态分布估计算法的卫星布局优化设计方法通过利用基于小生境算法和高斯分布估计算法更新机制的多模态分布估计算法，并在多模态分布估计算法中应用序列二次规划法局部优化机制和交叉算子，能够实现卫星布局设计问题的优化求解，获得在设定设计约束和设计目标下的最优卫星布局设计方案，且能有效地降低求解工作量。

需要说明的是，在本文中，诸如“第一”和“第二”等之类的关系术语仅仅用来将一个实体或者操作与另一个实体或操作区分开来，而不一定要求或者暗示这些实体或操作之间存在任何这种实际的关系或者顺序。而且，术语“包括”、“包含”或者其任何其他变体意在涵盖非排他性的包含，从而使得包括一系列要素的过程、方法、物品或者设备不仅包括那些要素，而且还包括没有明确列出的其他要素，或者是还包括为这种过程、方法、物品或者设备所固有的要素。此外，本文中“前”、“后”、“左”、“右”、“上”、“下”均以附图中表示的放置状态为参照。

最后应说明的是：以上实施例仅用于说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。