一种基于快速构建邻域覆盖的个人信用风险评估方法与流程

[0001]
本发明属于计算机科学与技术领域，具体涉及一种基于快速构建邻域覆盖的个人信用风险评估方法。


背景技术：

[0002]
随着信贷产业不断的发展，信贷数据量呈现爆炸式的增长，仅通过专业人员对贷款人的个人属性确定贷款人的信用好坏，不但会大量消耗人力物力，同时效率低下，甚至无法完成对贷款人评估。其次，贷款人的信息属性不仅多样化，而且属性之间往往具有一定的关联性。而粗糙集理论等数据挖掘方法可应用于个人信用风险评估中，能快速有效挖掘出贷款人的信息属性的关联性，达到较好的个人信用风险评估效果。
[0003]
粗糙集是由pawlak教授于1982提出的一种处理不精确、不一致、不完全信息和知识的重要数学工具，已经被广泛应用于机器学习、知识发现、数据挖掘、决策支持与分析等邻域。但是pawlak粗糙集只适用于处理离散型数据，而天津大学胡清华教授提出了基于邻域粒化的邻域粗糙集模型，实际上，邻域粗糙集提供了一种构造数据空间的近似方法。从拓扑学的角度，证明了邻域空间比数据空间的概念更一般化，这表明将原始数据空间转化为邻域空间有助于数据的泛化。
[0004]
现有技术中对个人信用风险评估的方法中包括5c要素分析法、财务比率综合分析法、多变量信用风险判别模型等等；例如多变量信用风险判别模型是以特征财务比率为解释变量，运用数量统计方法推导建立的标准模型。运用此模型预测某种性质事件发生的可能性，及时发现信用危机信号，使用户能及早的预防。但是上述方法中，需要大量的数据对模型进行训练，且由于训练的数据存在重叠，使得对模型的训练时间较长，消耗的能耗较多，训练得到的结果准确度低；因此，急需一种能提高检测效率的个人信用风险评估方法。


技术实现要素：

[0005]
为解决以上现有技术存在的问题，本发明提出了一种基于快速构建邻域覆盖的个人信用风险评估方法，该方法包括：获取贷款人的个人信息数据，将该信息数据输入到训练好的个人信用风险评估模型中进行风险评估，根据风险评估结果确定是否对贷款人进行贷款；
[0006]
对个人信用风险评估模型进行训练的过程包括：
[0007]
s1：获取贷款人的原始个人信息数据，将原始个人信息数据转化为决策信息表；
[0008]
s2：对决策信息表中的数据进行预处理；
[0009]
s3：采用k-means聚类算法对预处理后的数据进行聚类，构建邻域覆盖序列；
[0010]
s4：计算邻域覆盖序列中的邻域中心局部密度和相对距离；根据邻域中心的局部密度和相对距离对邻域进行排序；
[0011]
s5：对排序后的邻域进行选择，并对选择的邻域进行风险评估预测，得到预测结果。
[0012]
优选的，获取贷款人的个人信息数据包括账户状况、信贷历史、贷款金额、资产情况、住房情况、本银行信贷次数以及家庭成员收入情况。
[0013]
优选的，对决策信息表中的数据进行预处理的过程包括：采用当前数据属性均值对缺失的数据进行数据填充处理，将填充后的数据信息进行归一化处理。
[0014]
优选的，构建邻域覆盖序列的过程包括：
[0015]
s31：确定k个初始聚类中心；
[0016]
s32：根据初始聚类中心和k-means算法对样本数据进行聚类，得到k个类簇；
[0017]
s33：对得到的所有类簇进行初始化；计算所有的样本数据到初始聚类中心的距离；
[0018]
s34：根据计算的距离找到距离样本最近的聚类中心，并根据该聚类中心更新类簇；
[0019]
s35：根据更新后的类簇重新计算聚类中心，若计算后k个聚类中心不变，则输出k个类簇和聚类中心集合，否则返回步骤s33；
[0020]
s36：根据k个类簇和聚类中心集合计算聚类中心对应的邻域半径，根据邻域半径构建邻域。
[0021]
进一步的，重新计算聚类中心的公式为：
[0022][0023]
进一步的，邻域的公式为：
[0024]
o(v
i
)＝{x
j
∈cl
i
|δ(x
j
,v
i
)≤r(v
i
)}
[0025]
优选的，邻域中心v
i
的局部密度为：
[0026]
ρ
i
＝|o(v
i
)|
[0027]
邻域中心v
i
的相对距离为：
[0028]
δ
i
＝min{δ(v
i
,v
j
)|ρ
j
＞ρ
i
,o(v
j
)∈o}
[0029]
优选的，对选择的邻域进行风险评估预测的过程包括：
[0030]
若样本x仅处于单个邻域之中，则将该邻域的类别分配给样本x；
[0031]
若样本x处于多个邻域之中，设这多个邻域计算邻域集合o
inner
中邻域中心与x的距离，选择邻域中心到样本x最近的邻域，将最近的邻域的类别分配给样本x；
[0032]
若样本x不处于任意邻域之中，计算所有邻域中心与x的距离，选择邻域中心到样本x最近的邻域，将此邻域的类别分配给样本x。
[0033]
本发明的优点：
[0034]
1、通过采用本发明使用的方法，工作人员可根据预测结果辅助判断贷款人是否存在信用风险，能够极大的提高工作效率与服务质量；
[0035]
2、在传统基于邻域覆盖的规则学习方法中，需要计算所有样本的半径，从而得到初始邻域覆盖，进而通过邻域覆盖约简剔除冗余的邻域，整个过程需要大量的训练时间；本发明使用k-means算法形成邻域覆盖，从而减少邻域之间的重叠，能够达到线性的时间复杂度，大幅度减少模型的训练时间，且提出的半径能够规避离群样本的影响；
[0036]
3、通过邻域中心的局部密度与相对距离的乘积对邻域进行选择，能够更好的评估邻域的分类能力，使得在更少的邻域(规则)下得到更高的精度。
附图说明
[0037]
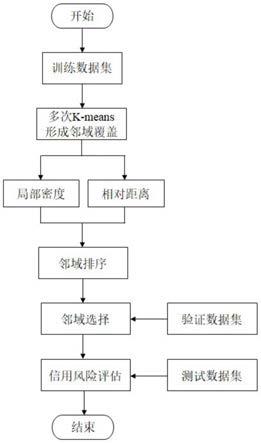
图1为本发明的个人信用风险评估方法流程图；
[0038]
图2为本发明的第一次聚类的结果图；
[0039]
图3为本发明的在进行邻域覆盖时的结果图；
[0040]
图4为本发明的一种实施例的邻域覆盖结果图；
[0041]
图5为本发明的一种实施例的用户预测结果图。
具体实施方式
[0042]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0043]
一种基于快速构建邻域覆盖的个人信用风险评估方法，如图1所示，该方法包括：获取贷款人的个人信息数据，将该信息数据输入到训练好的个人信用风险评估模型中进行风险评估，根据风险评估结果确定是否对贷款人进行贷款。
[0044]
对个人信用风险评估模型进行训练的过程包括：
[0045]
s1：获取贷款人的原始个人信息数据，将原始个人信息数据转化为决策信息表；
[0046]
s2：对决策信息表中的数据进行预处理；
[0047]
s3：采用k-means聚类算法对预处理后的数据进行聚类，构建邻域覆盖序列；
[0048]
s4：计算邻域覆盖序列中的邻域中心局部密度和相对距离；根据邻域中心的局部密度和相对距离对邻域进行排序；
[0049]
s5：对排序后的邻域进行选择，并对选择的邻域进行风险评估预测，得到预测结果。
[0050]
从企业数据库中采集贷款人的个人信息数据，其个人信息数据包括：账户状况、信贷历史、贷款金额、资产情况、住房情况、本银行信贷次数、家庭成员收入情况等属性。将上述个人信息数据转化为决策信息表＜u,a,d＞，其中，u＝{x1,x2,...,x
n
}为样本集合，a＝{a1,a2,...,a
m
}为条件属性集合，d为决策属性集。
[0051]
一种将个人信息数据转化为决策信息表的实施，其转换结果如表1所示，本实施例选取两列数据进行分析，其中u＝{x1,x2,...x
16
}，a＝{a1,a2}，d＝{d}＝{0,1}；若d＝1，则代表该贷款人高风险；若d＝0，则代表该贷款人低风险。
[0052]
表1.决策信息表
[0053][0054]
在对决策信息表中的数据进行分类预测中，把样本集合分割为训练数据集u
train
，验证数据集u
ver
和测试数据集u
test
。训练数据集用于模型训练，验证数据集用于寻找模型的最优参数，测试数据集用于评估模型；表1中“？”即为需要预测的样本；本实施例中，将u分为：u
train
＝{x1,x2,...,x
10
}，u
ver
＝{x
11
,x
12
,x
13
}和u
test
＝{x
14
,x
15
,x
16
}。
[0055]
对决策信息表中的数据进行预处理的过程包括：采用当前数据属性均值对缺失的数据进行数据填充处理，将填充后的数据信息进行归一化处理；对数据进行归一化处理的公式为：
[0056][0057]
其中，x
ij
表示第i个样本的第j个属性的值，min(x
j
)表示第j个属性的最小值，max(x
j
)表示第j个属性的最大值。
[0058]
对表1中的数据进行归一化处理后，得到的数据如表2所示：
[0059]
表2.归一化后的决策信息表
[0060][0061]
根据归一化后的决策信息表构建邻域覆盖序列。在构建邻域覆盖序列过程中，计算样本与样本之间的距离，本发明采用欧式距离公式计算各个样本之间的距离，并通过欧式距离来判断样本之间的相似程度。欧式距离越大，则样本间的相似度越低。其中，对于任意的样本x
i
和x
j
，即x
i
与x
j
的欧式距离定义为：
[0062][0063]
其中，x
ik
表示第i个样本下第k个属性的属性值。
[0064]
本发明采用k-means聚类算法构建邻域。确定k-means聚类算法的参数k值，本发明中k的参数值为k＝|d|，其中|
·
|表示集合的势(样本个数)；本发明中的k个聚类中心为相同类别样本的属性均值，在决策属性d下对给定的决策信息表＜u
train
,a,d＞和u
train
进行划
分，划分的表达式为：
[0065]
u
train
/{d}＝{x1,x2,...x
k
}
[0066]
其中，d表示决策属性，x
k
表示u
train
中第k个类别的样本集合。
[0067]
建邻域覆盖序列的过程包括：
[0068]
s31：确定k个初始聚类中心；初始聚类中心的公式为：
[0069][0070]
其中，v
i
表示聚类中心，cl
i
表示第i个类簇，x
j
表示类簇cl
i
中第j个样本，|x
i
|表示类簇中样本的个数，k表示类簇的数量。
[0071]
根据初始聚类中心的公式得到k个聚类中心v＝{v1,v2,...v
k
}，其中，v
k
表示第k个聚类中心。
[0072]
s32：根据初始聚类中心和k-means聚类算法对样本数据进行聚类，得到k个类簇。所示k个类簇为cl＝{cl1,cl2,...,cl
k
}；其中cl
k
表示第k个簇。
[0073]
s33：对得到的所有类簇进行初始化，即计算所有的样本数据到初始聚类中心的距离δ(x
i
,v
j
)。
[0074]
s34：找出所有样本距离自身最近的聚类中心，并根据该聚类中心更新类簇。对类簇进行更新的公式为：
[0075]
cl
j
＝cl
j
∪{x
i
}
[0076]
其中，∪表示对数据进行求并运算，{x
i
}表示u
train
中第i个样本形成的集合。
[0077]
s35：根据更新后的类簇重新计算聚类中心，若计算后k个聚类中心不变，则输出k个类簇和聚类中心集合，否则返回步骤s33。
[0078]
重新计算聚类中心的公式为：
[0079][0080]
其中，v
i
表示聚类中心，cl
i
表示第i个类簇，x
j
表示类簇cl
i
中第j个样本，|cl
i
|表示类簇cl
i
中样本的个数，k表示类簇的数量。
[0081]
s36：采用k个类簇和聚类中心集合构建邻域。
[0082]
对于和形成的邻域可以定义为：
[0083]
o(v
i
)＝{x
j
∈cl
i
|δ(x
j
,v
i
)≤r(v
i
)}
[0084]
其中，o(v
i
)表示覆盖的邻域，r(v
i
)表示中心v
i
的距离阈值，且r(v
i
)的计算公式为：
[0085]
r(v
i
)＝min(max{δ(v
i
,x
j
)|x
j
∈cl
i
},min{δ(v
i
,v
j
)|v
j≠i
∈v})
[0086]
为了使形成的邻域中包含所有的样本，首先计算类簇中样本与中心最远的距离值，但是直接取最大值，会被离群样本影响，导致邻域间出现过多的重叠部分。因此，在本发明中，计算出中心之间的距离，在类簇中样本与中心最远的距离值和中心之间的距离值选择最小的距离形成半径，既能尽可能包含更多的样本，又能避免离群样本的影响。且由于半径的选取，可能导致部分样本不存在任一邻域之中，但是此种样本往往是离群样本，因此直
接设置该样本形成的邻域的中心即为本身，半径设为0，此时形成的邻域集合o＝{o(v
i
)|i＝1,2,...,l}为数据样本u上的一个覆盖。
[0087]
由于在邻域集合o中存在部分邻域中有异类样本，那么对于有异类样本的邻域继续进行聚类，聚类方式以及邻域形成与上述一致，直到邻域集合o中所有邻域中均为同类样本时停止聚类。
[0088]
在第一次聚类中，时间复杂度为k-means聚类所产生的时间复杂度o(n)，在后续聚类中，仅需要分批对邻域中存在不同种类的样本进行聚类，时间复杂度远低于o(n)，且在计算出邻域半径时，需要构建邻域，这一步骤的时间复杂度为o(n)。因此，本发明构建邻域覆盖的时间复杂度为o(n)。
[0089]
一种构建邻域覆盖序列的具体实施例，对表2中的数据集u
train
＝{x1,x2,...,x
10
}构建邻域覆盖序列。首先通过决策属性对u
train
进行划分，得到u
train
/{d}＝{x1,x2}，其中x1＝{x1,x2,x3,x4,x5}，x2＝{x6,x7,x8,x9,x
10
}。计算得出初始聚类中心为v1＝(0.38,0.44)，v2＝(0.7,0.66)，通过k-means算法得到cl1＝{x1,x2,x3,x4}，cl2＝{x5,x6,x7,x8,x9,x
10
}；v1＝(0.3,0.45)，v2＝(0.7,0.62)；并计算出r(v1)＝0.18，r(v2)＝0.22。因此，可以得到邻域o(v1)＝{x1,x2,x3,x4}和o(v2)＝{x5,x6,x7,x8,x9,x
10
}。第一轮聚类后邻域产生的图像如图2所示。
[0090]
从图2中可知邻域o(v2)中出现不同类的样本，只需对o(v2)中的样本继续聚类，步骤与第一轮相同。最终得到样本集合u上的一个覆盖o＝{o(v1),o(v2),o(v3)}，其中o(v1)＝{x1,x2,x3,x4},r(v1)＝0.18；o(v2)＝{x6,x7,x8,x9,x
10
},r(v2)＝0.12；o(v3)＝{x5},r(v3)＝0。覆盖o所形成的结果如图3所示。
[0091]
为了同时刻画邻域的分类能力以及邻域之间的多样性，本发明通过邻域中心的局部密度和邻域中心的相对距离的乘积对邻域进行排序。对于邻域中心v
i
的局部密度为：
[0092]
ρ
i
＝|o(v
i
)|
[0093]
其中，|
·
|表示集合的势(样本个数)。
[0094]
邻域o(v
i
)的局部密度即为o(v
i
)中的样本个数，邻域中心v
i
的相对距离公式为：
[0095]
δ
i
＝min{δ(v
i
,v
j
)|ρ
j
＞ρ
i
,o(v
j
)∈o}
[0096]
其中，ρ
i
表示邻域中心v
i
的局部密度，ρ
j
表示邻域中心v
j
的局部密度。若在所有邻域中心中v
i
的局部密度最大，则δ
i
＝max{δ(v
i
,v
j
)|o(v
j
)∈o}。
[0097]
根据邻域中心的局部密度以及相对距离，本发明采用综合变量γ对所有邻域进行从大到小的排序，综合变量计算公式为：
[0098]
γ
i
＝ρ
i
*δ
i
[0099]
以表2中的数据作为本发明排序的一种实施例，根据综合变量计算公式可以得到γ1＝1.72，γ2＝2.15，γ3＝0.22，根据γ值对邻域进行从大到小的排序，得到排序后的邻域集合o
r
＝{o(v2),o(v1),o(v3)}。
[0100]
由于邻域中所有的样本都是同类的，因此每个邻域对应一个分类规则，可用于对测试数据集的分类(个人信用风险评估)。但是，如果将所有邻域形成的规则对测试数据集中的样本进行预测，容易受到噪声样本以及离群样本的影响。因此，本发明通过验证数据集选择前h邻域，在通过这前h邻域对测试数据集进行预测评估。设待评估样本为x，预测的规
则为：
[0101]
(1)若样本x仅处于单个邻域之中，则将该邻域的类别分配给样本x。
[0102]
(2)若样本x处于多个邻域之中，设这多个邻域计算邻域集合o
inner
中邻域中心与x的距离，选择邻域中心到样本x最近的邻域，将最近的邻域的类别分配给样本x。
[0103]
(3)若样本x不处于任意邻域之中，计算所有邻域中心与x的距离，选择邻域中心到样本x最近的邻域，将此邻域的类别分配给样本x。
[0104]
一种对选择的邻域进行风险评估预测的实施例，根据邻域集合o
r
＝{o(v2),o(v1),o(v3)}与验证数据集u
ver
得出如图4所示的结果。根据上述预测规则可以得出，当h＝1时，预测精度为33％；当h＝2时，预测精度为100％；当h＝3时，预测精度为100％。因此，选择前h＝2个邻域，即
[0105]
根据邻域集合和验证数据集u
test
得到如图5所示的结果图，从图5中可以看出样本x
14
,x
15
均不处于任意邻域，则通过规则(3)进行分配，得出样本x
14
的类别为1，因此样本x
14
为高风险用户；样本x
15
的类别为0，因此样本x
15
为低风险用户；对于样本x
16
处于单个邻域o(v2)中，则通过规则(1)，得出x
16
的类别为0，因此样本x
16
为低风险用户。
[0106]
以上所举实施例，对本发明的目的、技术方案和优点进行了进一步的详细说明，所应理解的是，以上所举实施例仅为本发明的优选实施方式而已，并不用以限制本发明，凡在本发明的精神和原则之内对本发明所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。