一种流体锂氧电池功率平衡模型算法的制作方法

本发明属于流体锂氧电池功率平衡领域，具体涉及一种流体锂氧电池功率平衡模型算法。

背景技术：

随着可再生能源技术的发展，氧化还原流体锂氧电池(rfbs)作为电能存储系统(ees)越来越受到关注，其主要优点为设计灵活性，能量/功率解耦可行性，同时可以减少不常用电池组件的数量。

尽管目前人们使用不同的化学物质(催化剂、氧化还原介质、有机电解液、锂插层流动电极、微/纳米结构材料)来提高动力电池的性能，但多数研究成果主要集中在材料科学上。arenas等人提出对流体锂氧电池的结构和实际性能进行工程研究，评价电池的整体功率平衡。材料科学应用中，电化学模型方法将推动锂离子电池、锂硫电池和流体锂氧电池等新型储能技术的发展。锂氧离子(li2o2)是一种绝缘材料，在放电过程中，随着li2o2在阴极上的形成，电池的过电位增大。li2o2限制了电池的放电容量，导致充电电压上限高于3.7v。同时，在高化学反应性化合物(如过氧化物和超氧物)存在的情况下，高压充电会降低电解液和碳电极的化学稳定性，减少电池的循环寿命。laoire和peng深入研究电解液组成对流体锂氧电池性能的影响程度。monaco等人利用电池流体力学设计原理，显著提高电池的效率响应。

实际应用中，流动循环的能量消耗降低了锂流电池的整体效率。相应的功率损耗(ploss)为锂电池的体积流量速率(v)和压降(δp)的乘积，即：

上式中，η为流速效率。在设计良好的流动性rfb中，ploss可以降到2％～4％。但是，使用粘性和半固态流体会增加功率损耗，其值不可忽略。zeng等人证明了平均速度为v的流体通过长度为l的玻璃态碳(rvc)电极，δp可以由forchheimer方程模拟：

δp/l＝(μ/k)·v+(ρβ/2)·v²

式中，μ和ρ分别是液体电解质的动态粘度和密度。k表示rvc磁导率，即对穿过多孔介质的流动粘性阻力。β为流体的惯性因子，表示路径弯曲引起的流体加速/减速的微观惯性效应。

技术实现要素：

本发明的目的是克服现有技术中的不足，提供一种流体锂氧电池功率平衡模型算法。

这种流体锂氧电池功率平衡模型算法，包括以下步骤：

步骤1、设计测试单体电池的测试装置；设置测试压降条件，并测量不同阴极离子流速vrvc下，流体锂氧电池的实际输出功率；

步骤2、建立锂氧流单体电池的输出功率pout的半经验模型，利用测试数据计算锂氧流单体电池的输出功率pout和功率损耗ploss；

步骤3、设计长度l、宽度w和厚度σ的棱柱状堆栈流体锂氧电池结构模型；

步骤4、计算棱柱状堆栈流体锂氧电池模型的输出功率pout，建立棱柱状堆栈流体锂氧电池的输出功率pout与体积的半经验拟合函数，电流大小、锂氧流单体电池的输出功率pout和功率损耗ploss与玻璃态碳电极(rvc)面积相关；计算功率损失ploss和净功率pn；

步骤5、设计最大限度地提高锂氧流单体电池的输出功率pout且减少锂氧流单体电池的功率损失ploss的多孔玻璃态碳电极(rvc)：利用两片gf/f-whatman玻璃纤维过滤器，分离多孔玻璃态碳电极(rvc)和锂离子电极，为了避免锂表面被溶解在阴极中的氧气污染，允许锂/多孔玻璃态碳电极(rvc)堆积层存在不对称位移。

作为优选，步骤1具体包括如下步骤：

步骤1.1、设置测试压降条件：增大测试装置中锂氧流单体电池(flob电池)内多孔玻璃态碳电极(rvc)的入口面积，减小多孔玻璃态碳电极(rvc)的出口面积，使流体锂氧电池的流量通道压降分布均匀；

步骤1.2、在多孔玻璃态碳电极(rvc)中不同阴极离子流速vrvc下，测量流体锂氧电池的实际输出功率和与流体锂氧电池的阴极离子流速vrvc相关的功率损失；对玻璃态碳电极(rvc)的磁导率k和惯性因子β进行实验评估。

作为优选，步骤2具体包括如下步骤：

步骤2.1、计算锂氧流单体电池的输出功率pout，建立锂氧流单体电池的输出功率pout的半经验模型：

将流体锂氧电池的实际输出功率与流体锂氧电池的阴极离子流速vrvc关联，设锂氧流单体电池的输出功率pout只取决于阴极面积，阴极面积与玻璃态碳电极(rvc)总孔表面和体积相关；记录不同充放电电压条件下锂氧流单体电池的输出功率pout与阴极离子流速vrvc，并将记录的锂氧流单体电池的输出功率pout与阴极离子流速vrvc拟合得到关系曲线；利用插值算法建立锂氧流单体电池的输出功率pout的半经验模型：

上式中，为锂氧流单体电池的输出功率密度，a和p0为拟合常数，vτ为与时间常数相关的流速，vrvc为玻璃态碳电极(rvc)中的阴极离子流速；

步骤2.2、测得不同阴极体积流量速率v下通过流体锂氧电池的压降δp，并记录该值；计算锂氧流单体电池的与阴极离子相关的功率损耗ploss：

上式中，η为流速效率，δp为压降，v为体积流量速率；则功率损失ploss取决于沿流动方向穿过多孔玻璃态碳电极(rvc)的压降δp和体积流量速率v；由forchheimer方程得压降δp取决于玻璃态碳电极(rvc)的磁导率k、惯性因子β和多孔玻璃态碳电极(rvc)的长度l；forchheimer方程为：

δp/l＝(μ/k)·v+(ρβ/2)·v²(3)

上式中，μ为液体电解质的动态粘度；ρ是液体电解质的密度；k表示玻璃态碳电极(rvc)的磁导率，磁导率k为对穿过多孔介质的流动粘性阻力；β为流体的惯性因子，表示路径弯曲引起的流体加速/减速的微观惯性效应。

作为优选，步骤4具体包括如下步骤：

步骤4.1、建立棱柱状堆栈流体锂氧电池的输出功率pout与体积的半经验拟合函数，在给定阴极离子流速vrvc条件下，将棱柱状堆栈流体锂氧电池的输出功率pout与玻璃态碳电极(rvc)的体积关联：

上式中，pout为棱柱状堆栈流体锂氧电池的输出功率，w为玻璃态碳电极(rvc)的宽度，l为玻璃态碳电极(rvc)的长度，σ为玻璃态碳电极(rvc)的厚度，a和p0为拟合常数，vrvc为多孔玻璃态碳电极(rvc)中的阴极离子流速，vτ为与时间常数相关的流速；为锂氧流单体电池的输出功率密度，计算方式为：

步骤4.2、建立体积流量速率与多孔玻璃态碳电极(rvc)尺寸的关系方程：

上式中，vrvc为多孔玻璃态碳电极(rvc)中的阴极离子流速，ε为多孔玻璃态碳电极(rvc)的空隙率；σ为玻璃态碳电极(rvc)的厚度，w为玻璃态碳电极(rvc)的宽度；

步骤4.3、结合forchheimer方程和式(5)计算功率损失ploss和净功率pn：

上式中，a和p0为拟合常数；为拟合常数p0的平均值；δp为压降；为多孔玻璃态碳电极的体积流量速率；μ为液体电解质的动态粘度；ρ是液体电解质的密度；β为流体的惯性因子；vrvc为多孔玻璃态碳电极(rvc)中的阴极离子流速；w为玻璃态碳电极(rvc)的宽度，l为玻璃态碳电极(rvc)的长度，σ为玻璃态碳电极(rvc)的厚度，ε为多孔玻璃态碳电极(rvc)的空隙率；pout为锂氧流单体电池的输出功率；

上式(7)表明净功率pn随着多孔玻璃态碳电极(rvc)的体积增大而增加；在恒定多孔玻璃态碳电极(rvc)体积条件下改变锂氧流单体电池(flob电池)的几何结构，对增强锂氧流单体电池的输出功率pout与功率损失ploss没有影响，因为两个参数具有相同的线性依赖性(w·l·σ)；上式(4)至上式(6)表明锂氧流单体电池的功率损失ploss和阴极离子流速vrvc在指数和多项式方面存在不同的增长速率。

作为优选，步骤1中测试装置包括储气罐、流体锂氧电池、压力计和蠕动泵；储气罐一端连接蠕动泵一端，蠕动泵另一端连接流体锂氧电池一端，流体锂氧电池另一端连接储气罐另一端，形成回路；压力计的两端并联在流体锂氧电池两端上。

作为优选，步骤1中单体电池的充放电电压范围为2.3v～2.7v。

作为优选，步骤2.1中计算锂氧流单体电池的输出功率pout的方式为：pout＝电流*电池的充放电电压。

本发明的有益效果是：本发明提出的流体锂氧电池功率平衡模型针对复杂电池系统，在不需要获得动态数据的前提下，描述流体锂氧电池的特殊化学组成和反应过程；本发明设计一种合理的多孔玻璃态碳电极(rvc)及测试该单体电池的测试装置，最大化输出功率且最小化功率损耗；半经验模型将拦截阴极流体的三维多孔阴极的几何结构与净功率输出进行函数关联，给出了净功率输出与锂氧流流速的关系方程，同时考虑单体电池的特殊化学过程和结构组成；充分开发了流体锂氧电池的化学特性。

附图说明

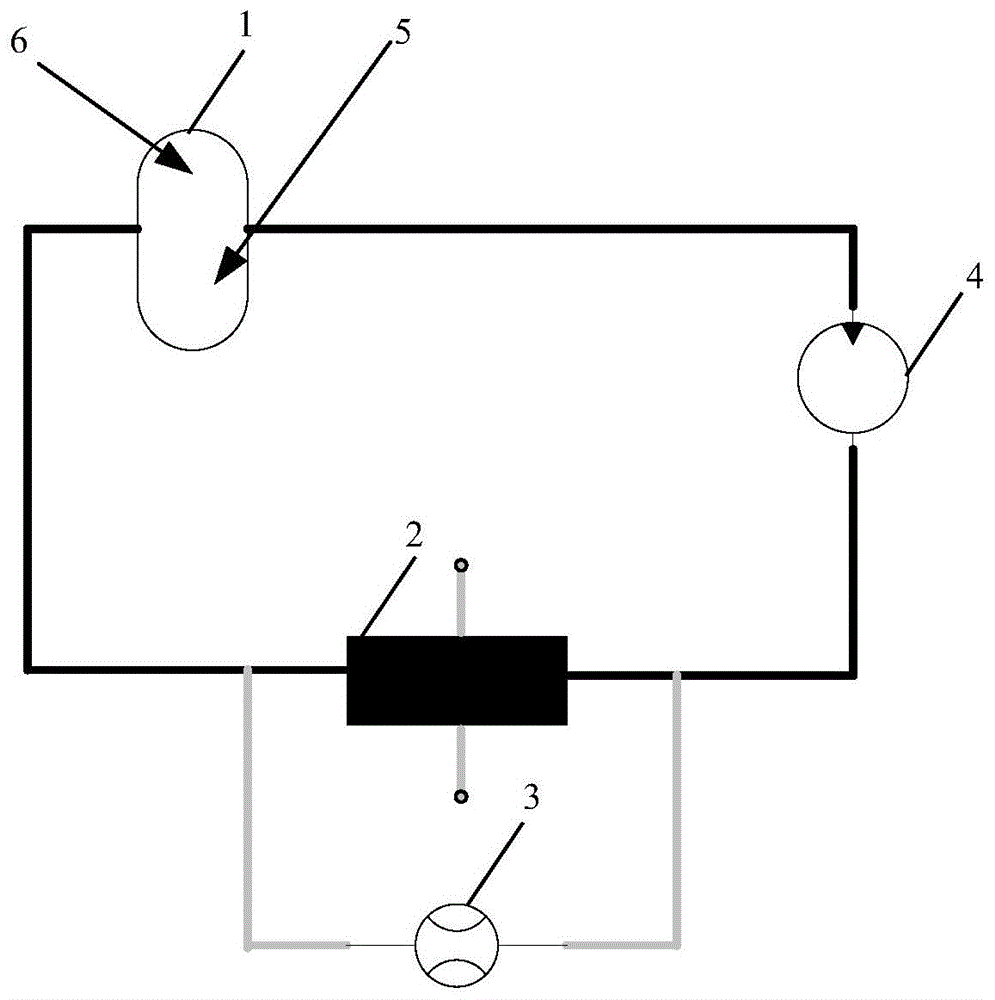
图1为测试单体电池的实验装置图；

图2为输出功率密度与阴极离子流速关系曲线图；

图3为长度l、宽度w和厚度σ的棱柱状堆栈电池结构模型图；

图4为在蠕动泵泵速为200rpm时(阴极离子流速不同)，不同电池电压(2.6v、2.5v、2.4v和2.3v)flob放电电流分布曲线图；

图5为输出功率pout与单体电池电压的关系曲线图；

图6为不同泵速条件下输出功率pout和损耗功率ploss的比较曲线图；

图7中(a)为流体速度vrvc与蠕动泵泵速关系图；(b)为不同几何形状(g1,g2和g3)条件下，pout与蠕动泵泵速的关系曲线图；(c)为不同几何形状(g1,g2和g3)条件下，ploss与蠕动泵泵速的关系曲线图；(d)为净功率pn随蠕动泵泵速变化曲线图。

附图标记说明：储气罐1、流体锂氧电池2、压力计3、蠕动泵4、外部气体5、内部气体6。

具体实施方式

下面结合实施例对本发明做进一步描述。下述实施例的说明只是用于帮助理解本发明。应当指出，对于本技术领域的普通人员来说，在不脱离本发明原理的前提下，还可以对本发明进行若干修饰，这些改进和修饰也落入本发明权利要求的保护范围内。

本发明提出流体锂氧电池实际功率性能的实验评估方法和建模方法。设计一种新型半经验模型，建立电池净功率输出与锂氧流流速的关系方程。

作为一种实施例，一种流体锂氧电池功率平衡模型算法，具体为：

步骤1、如图1所示，设计测试单体电池的测试装置，该测试装置包括储气罐1、锂氧流单体电池(flob电池)2、压力计3和蠕动泵4；储气罐1一端连接蠕动泵4一端，蠕动泵4另一端连接锂氧流单体电池2一端，锂氧流单体电池2另一端连接储气罐1另一端，形成回路；压力计3的两端并联在锂氧流单体电池2两端上；

步骤1.1、设置测试压降条件：增大测试装置中锂氧流单体电池(flob电池)2内多孔玻璃态碳电极(rvc)的入口面积，减小多孔玻璃态碳电极(rvc)的出口面积，使锂氧流单体电池(flob电池)2的流量通道压降分布均匀；

步骤1.2、在多孔玻璃态碳电极(rvc)中不同阴极离子流速vrvc下，测量流体锂氧电池的实际输出功率和与流体锂氧电池的阴极离子流速vrvc相关的功率损失；对玻璃态碳电极(rvc)的磁导率k和惯性因子β进行实验评估；

步骤2、利用测试数据估计锂氧流单体电池的输出功率pout和功率损耗ploss；

步骤2.1、计算锂氧流单体电池的输出功率pout，建立锂氧流单体电池的输出功率pout的半经验模型：

将流体锂氧电池的实际输出功率与流体锂氧电池的阴极离子流速vrvc关联，设锂氧流单体电池的输出功率pout只取决于阴极面积，阴极面积与玻璃态碳电极(rvc)总孔表面和体积相关；记录不同充放电电压条件下锂氧流单体电池的输出功率pout与阴极离子流速vrvc，并将记录的锂氧流单体电池的输出功率pout与阴极离子流速vrvc拟合得到关系曲线，图2为不同充放电电压条件下的实验数据与拟合数据(实点为实验数据，实线为拟合数据的拟合曲线)；利用插值算法建立锂氧流单体电池的输出功率pout的半经验模型：

上式中，为锂氧流单体电池的输出功率密度，a和p0为拟合常数，vτ为与时间常数相关的流速，vrvc为玻璃态碳电极(rvc)中的阴极离子流速；

步骤2.2、由压力计3测得不同阴极体积流量速率v下通过流体锂氧电池的压降δp，并记录该值；计算锂氧流单体电池的与阴极离子相关的功率损耗ploss：

上式中，η为流速效率，δp为压降，v为体积流量速率；则功率损失ploss取决于沿流动方向穿过多孔玻璃态碳电极(rvc)的压降δp和体积流量速率v；由forchheimer方程得压降δp取决于玻璃态碳电极(rvc)的孔隙度磁导率k、惯性因子β和多孔玻璃态碳电极(rvc)的长度l；forchheimer方程为：

δp/l＝(μ/k)·v+(ρβ/2)·v²(3)

上式中，μ为液体电解质的动态粘度；ρ是液体电解质的密度；k表示玻璃态碳电极(rvc)的磁导率，磁导率k为对穿过多孔介质的流动粘性阻力；β为流体的惯性因子，表示路径弯曲引起的流体加速/减速的微观惯性效应；

步骤3、如图3所示，设计长度l、宽度w和厚度σ的棱柱状堆栈流体锂氧电池结构模型；设定三种rvc几何形状记为g1、g2和g3，三种几何形状具有相同的厚度、体积和横截面积，根据不同长宽比定义g1为细长几何体，g2为正方形几何体，g3为大几何体。三种几何形状的长宽比分别为，g1：l＝10cm和w＝1cm(细长几何体)，g2：l＝w＝3.16cm(正方形几何体)，g3：l＝1cm和w＝10cm(大几何体)；

步骤4、计算棱柱状堆栈流体锂氧电池模型的功率值，电流大小、锂氧流单体电池的输出功率pout和功率损耗ploss与玻璃态碳电极(rvc)面积相关；

步骤4.1、建立棱柱状堆栈流体锂氧电池的输出功率pout与体积的半经验拟合函数，在给定阴极离子流速vrvc条件下，将棱柱状堆栈流体锂氧电池的输出功率pout与玻璃态碳电极(rvc)的体积关联：

上式中，pout为棱柱状堆栈流体锂氧电池的输出功率，w为玻璃态碳电极(rvc)的宽度，l为玻璃态碳电极(rvc)的长度，σ为玻璃态碳电极(rvc)的厚度，a和p0为拟合常数，vrvc为多孔玻璃态碳电极(rvc)中的阴极离子流速，vτ为与时间常数相关的流速；为锂氧流单体电池的输出功率密度，计算方式见式(1)；

步骤4.2、建立体积流量加速度与多孔玻璃态碳电极(rvc)尺寸的关系方程：

上式中，vrvc为多孔玻璃态碳电极(rvc)中的阴极离子流速，ε为多孔玻璃态碳电极(rvc)的空隙率；σ为玻璃态碳电极(rvc)的厚度，w为玻璃态碳电极(rvc)的宽度；

步骤4.3、结合式(2)、式(3)和式(5)计算功率损失ploss和净功率pn：

上式中，a和p0为拟合常数；为拟合常数p0的平均值；δp为压降；μ为液体电解质的动态粘度；ρ是液体电解质的密度；β为流体的惯性因子；vrvc为多孔玻璃态碳电极(rvc)中的阴极离子流速；w为玻璃态碳电极(rvc)的宽度，l为玻璃态碳电极(rvc)的长度，σ为玻璃态碳电极(rvc)的厚度，ε为多孔玻璃态碳电极(rvc)的空隙率；pout为锂氧流单体电池的输出功率；

上式(7)表明净功率pn随着多孔玻璃态碳电极(rvc)的体积增大而增加；在恒定多孔玻璃态碳电极(rvc)体积条件下改变锂氧流单体电池(flob电池)的几何结构，对增强锂氧流单体电池的输出功率pout与功率损失ploss没有影响，因为两个参数具有相同的线性依赖性(w·l·σ)；上式(4)至上式(6)表明锂氧流单体电池的功率损失ploss和阴极离子流速vrvc在指数和多项式方面存在不同的增长速率；

步骤5、设计一种最大限度地提高锂氧流单体电池的输出功率pout且减少锂氧流单体电池的功率损失ploss的多孔玻璃态碳电极(rvc)：利用两片gf/f-whatman玻璃纤维过滤器，分离多孔玻璃态碳电极(rvc)和锂离子电极，为了避免锂表面被溶解在阴极中的氧气污染，允许锂/多孔玻璃态碳电极(rvc)堆积层存在不对称位移。

实验结果1：

通过蠕动泵4控制泵速为200rpm时，电池电压分别为2.6v、2.5v、2.4v和2.3v的锂氧流单体电池(flob电池)的电流分布曲线如图4所示；由于氧在电极上的传输质量得到改善，流量的增加能够改善不同电压数值下的电流值；在给定的流速下，电流随电池极化而增加。

实验结果2：

控制泵速分别为0rmp、50rmp、100rmp和150rmp，通过将电流乘以电池电压来计算锂氧流单体电池的输出功率pout，得到如图5所示锂氧流单体电池的输出功率pout与电池电压的关系图；由图可知：

1)泵速越大，锂氧流单体电池的输出功率pout越大；

2)在相同泵速条件下，输出功率pout越大，电池电压越小；

3)若泵速增大，则输出功率随着电压增大减小更快。

实验结果3：

得到不同泵速条件下输出功率pout和损耗功率ploss的比较曲线如图6所示，图6中实折线为功率损耗ploss，4条虚曲线为不同电池电压的输出功率pout。结果表明，本实施例的单体电池具有正能量平衡(pout>ploss)的可行性区域，该可行性区域在0到30rpm之间。

实验结果4：

考虑流体速度与蠕动泵速率关系，图7(a)表示对应的流体速度vrvc，图7(b)和图6(c)表示不同的几何形状(g1,g2和g3)条件下，pout和ploss与泵速的关系曲线。由图可知：

1)流速增加(体积从g3变到g1)，pout和ploss同时增加；

2)几何形状g1的输出功率pout最高，可以达到20mw，几何形状g3的功率损耗ploss最小；

3)pout和ploss的变化趋势随着锂氧流体的流速变化不同而不同；(4)图7(d)为净功率pn随流速变化曲线。由图可知，pn在vrvc＝0m/s时达到最大值，并随rvc的体积大小不同而不同。

4)实验证明，在蠕动泵速率范围内，最大化净功率增益的最佳几何结构是具有最大流量横截面积的几何结构g3。