一种风电机组滚动轴承故障诊断方法

1.本发明涉及机电设备的状态监测与故障诊断技术领域。


背景技术：

2.近年来，风能作为一种绿色能源在世界能源结构中发挥的作用愈来愈重要，与此同时，风电相关装备也因此得到迅猛发展。在风电机组各种故障中，传动系统故障虽然故障次数不是最多的，但是其故障导致的停机时间却是最长的。因此，研究风电机组滚动轴承的故障诊断对降低影响风电机组安全、稳定运行的风险会有实际意义。
3.传统意义上的故障诊断方法大多采用阈值判别的方式，这种方式存在的主要缺点是常常难以客观地反映故障与特征之间的准确规律。风电机组滚动轴承的振动信号是一种典型的时间序列信号，提取的时频故障特征依然保持着其时序信息，虽然人工神经网络、模糊理论、支持向量机等智能诊断方法被用于滚动轴承的故障诊断中，表现出了较好的诊断效果，但是这些诊断方法没有充分利用滚动轴承振动信号的时序特征，其诊断结果仍未达到理想的效果。
4.其中，bp神经网络是较递归神经网络应用较早的方法，但是随着其应用的深入，其自身的局限性也逐渐显现出来，如可能陷入局部最优值，网络的收敛速率较慢，样本依赖性强等缺陷。针对这些缺陷出现了许多改进的方法，比如利用lm方法对bp神经网络进行改进，该方法兼有梯度法和牛顿法的优点，从而显著增加了bp神经网络的诊断精确性，同时加快了bp神经网络的收敛速率。通过实验对bp神经网络和递归神经网络，在故障诊断方面所表现出的性能做了充分地比较，表明了递归神经网络在算法收敛速度、诊断结果精确性和算法稳定性方面与bp神经网络相比，均有良好改善。递归神经网络在故障诊断中的优势逐渐显现出来，其应用也随之增多。但是传统的递归神经网络也有其自身的缺点，如在每次回馈的过程中信息都会出现部分损失，时间积累到一定的时候，初始信息就会退化，出现梯度消失效应。


技术实现要素：

5.本发明要解决的技术问题是提供一种风电机组滚动轴承故障诊断方法，它具有故障判断准确率高的特点。
6.为解决上述技术问题，本发明所采取的技术方案是：
7.一种风电机组滚动轴承故障诊断方法，包括如下步骤：
8.a.将振动传感器安装在滚动轴承的外壳上，用于采集滚动轴承的轴承振动信号，设得到的采集的轴承振动信号为：
[0009][0010]
式中，n为样本点数目，j为第j个采样点，t＝{1,2,
…
,n}，j＝{1,2,
…
,n}，采样频率为f
s
；
[0011]
b.对步骤a中所采集的振动信号x
j
(t)(t＝1,2,
…
,n)进行l层小波包分解，振动信
号在第k层第t
′
点处的小波包分解系数递推公式如下：
[0012][0013][0014]
式中，m为滤波器系数序号，i＝{0,1,2,
…
,2
k
‑
1}为小波包子空间序号，k＝{0,1,2,
…
,l}为分解尺度，h(m)和g(m)为一对正交镜像滤波器；
[0015]
经过l层小波包分解，原振动信号被划分为2
l+1
‑
2个小波包子空间，各子空间对应的频带为：
[0016][0017]
式中，f
s
为采样频率；
[0018]
c.根据步骤b中所得到的各子空间对应的频带，计算振动信号在小波包最佳子空间下的特征矢量，其具体方法如下：
[0019]
a).定义振动训练样本集，振动训练样本集包括风电机组滚动轴承正常状态下的正常训练样本和各故障状态下的故障振动训练样本，振动训练样本集在特征空间v
i
中有c个类别，其分别是(v1,v2,
…
,v
c
)，振动训练样本集为其中表示第r类的第s个q维的振动训练样本，n
s
为第r类中振动训练样本的个数，n
q
为振动训练样本的维数；
[0020]
b).计算振动训练样本的平均类内距离和平均类间距离，计算公式为：
[0021][0022][0023]
式中，分别表示所有样本第q维的重心和第r类中的样本第q维的重心；
[0024]
c).定义距离准则d
s
，其定义公式为：
[0025][0026]
由步骤c)可计算出1
‑
l各尺度下的所有2
l+1
‑
2个子空间的距离准则d
s
的值；
[0027]
d).确定最佳小波包子空间,设l
′
尺度下的第p个子空间的距离准则值为其中l
′
＝(1,2,
…
,l)，p＝(1,2,
…
,2
l
′
)；若满足则对应的子空间为最佳小波包子空间；
[0028]
e).计算步骤a中所采集的轴承振动信号在所有最佳小波包子空间上的能量，计算
方法如下式所示：
[0029][0030]
式中，x
j
(i)为第j个最佳小波包子空间的第i个能量系数，n
j
为最佳小波包子空间总数；
[0031]
f).最佳小波包子空间上的能量提取出来之后，将其作为风电机组滚动轴承特征矢量；
[0032]
d.将风电机组滚动轴承的特征矢量输入到bp神经网络中，实现风电机组的故障诊断。
[0033]
采用上述技术方案所产生的有益效果在于：
[0034]
循环神经网络(recurrent neural network,rnn)模型以其更高的非线性能力，更高的精度和收敛速度，在旋转机械故障诊断中表现出了极强的生命力，非常适合处理带有时间信息的序列数据。但是传统的rnn在每次误差反馈的过程中信息都会出现部分损失，时间积累到一定的时候，初始信息就会退化，出现梯度消失效应。因此，传统rnn丧失了长时间记忆的能力，而长短时记忆(long short
‑
term memory,lstm)神经网络通过引入记忆元，可以解决梯度消失的问题。
[0035]
本发明利用小波包变换处理复杂的、非线性、非平稳的风电机组滚动轴承振动信号，有效提取出其故障特征，并采用gru(gated recurrent unit)模型(结构图如图1所示)作为长短时记忆神经网络的记忆单元，进行风电机组滚动轴承的故障诊断，该方法与传统rnn相比能够有效处理具有长时间依赖关系的信号，长时间记忆的能力，有效解决了传统rnn存在的梯度消失问题，并且与一般的意义上的长短时记忆神经网络相比，gru模型更简单，训练速度更快，适合处理较大规模的数据。
[0036]
它具有故障判断准确率高的特点。
附图说明
[0037]
图1是gru型作为长短时记忆神经网络记忆单元结构图；
[0038]
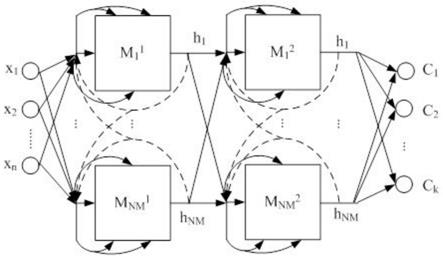
图2是本发明所建立以gru型长短时记忆神经网络为核心的用于故障诊断的网络架构；
[0039]
图3是整体算法流程图。
具体实施方式
[0040]
下面将结合附图和具体实施例对本发明进行进一步详细说明。
[0041]
本发明提出了一种基于gru型长短时记忆神经网络的风电机组故障轴承故障诊断方法，通过利用gru型长短时记忆神经网络模型快速处理具有长时间依赖关系的信号的优势，结合小波包变换给出了一种新的适合风电机组滚动轴承的故障诊断方法。该方法首先采用小波包变换将具有非线性、非平稳特征的滚动轴承振动信号划分为多个小波包子空间；然后基于分类距离准则选取小波包最佳子空间，选取出若干最佳小波包子空间；然后计算每个最佳小波包上的能量值，将其作为滚动轴承的故障特征；最后将滚动轴承的故障特征输入到本发明所建立的诊断网络，从而实现风电机组滚动轴承的故障诊断。
[0042]
一种风电机组滚动轴承故障诊断方法，包括如下步骤：
[0043]
a.将振动传感器安装在滚动轴承的外壳上，用于采集滚动轴承的轴承振动信号，设得到的采集的轴承振动信号为：
[0044][0045]
式中，n为样本点数目，j为第j个采样点，t＝{1,2,
…
,n}，j＝{1,2,
…
,n}，采样频率为f
s
；
[0046]
b.对步骤a中所采集的振动信号x
j
(t)(t＝1,2,
…
,n)进行l层小波包分解，振动信号在第k层第t
′
点处的小波包分解系数递推公式如下：
[0047][0048][0049]
式中，m为滤波器系数序号，i＝{0,1,2,
…
,2
k
‑
1}为小波包子空间序号，k＝{0,1,2,
…
,l}为分解尺度，h(m)和g(m)为一对正交镜像滤波器；
[0050]
经过l层小波包分解，原振动信号被划分为2
l+1
‑
2个小波包子空间，各子空间对应的频带为：
[0051][0052]
式中，f
s
为采样频率；
[0053]
c.根据步骤b中所得到的各子空间对应的频带，计算振动信号在小波包最佳子空间下的特征矢量，其具体方法如下：
[0054]
a).定义振动训练样本集，振动训练样本集包括风电机组滚动轴承正常状态下的正常训练样本和各故障状态下的故障振动训练样本，振动训练样本集在特征空间v
i
中有c个类别，其分别是(v1,v2,
…
,v
c
)，振动训练样本集为其中表示第r类的第s个q维的振动训练样本，n
s
为第r类中振动训练样本的个数，n
q
为振动训练样本的维数；
[0055]
b).计算振动训练样本的平均类内距离和平均类间距离，计算公式为：
[0056][0057][0058]
式中，分别表示所有样本第q维的重心和第r类中的样本第q维的重心；
[0059]
c).定义距离准则ds，其定义公式为：
[0060][0061]
由步骤c)可计算出1
‑
l各尺度下的所有2
l+1
‑
2个子空间的距离准则d
s
的值；
[0062]
d).确定最佳小波包子空间,设l
′
尺度下的第p个子空间的距离准则值为其中l
′
＝(1,2,
…
,l)，p＝(1,2,
…
,2
l
′
)；若满足则对应的子空间为最佳小波包子空间；
[0063]
e).计算步骤a中所采集的轴承振动信号在所有最佳小波包子空间上的能量，计算方法如下式所示：
[0064][0065]
式中，x
j
(i)为第j个最佳小波包子空间的第i个能量系数，n
j
为最佳小波包子空间总数；
[0066]
f).最佳小波包子空间上的能量提取出来之后，将其作为风电机组滚动轴承特征矢量；
[0067]
d.将风电机组滚动轴承的特征矢量输入到bp神经网络中，实现风电机组的故障诊断。
[0068]
详细过程如下：
[0069]
若模型的输入序列为x，在时刻t时，第l层的第j个记忆单元的状态可用以下公式表示：
[0070][0071][0072][0073][0074]
式中，sigm为logistic sigmoid函数，w为相应的权重，b为偏置，为t时刻第l层第j个gru记忆单元的最终输出值；
[0075]
e.将步骤d中gru型长短时记忆神经网络的输出作为softmax多分类器的输入，实现风电机组滚动轴承在多个故障模式下的分类问题。通过最小化代价函数计算每一种分类结果出现的概率，如果某一概率值最大，即可确定当前的故障模式；
[0076]
采用softmax回归的方法，分别计算每种故障模式j的概率p(y＝j|x)大小作为故障模式的分类依据。假设风电机组滚动轴承有k个故障模式，输入为x，则softmax回归系统的假设函数h
θ
(x)的形式如下：
[0077][0078]
式中，是该模型的参数，此时参数θ表示全部的模型参数，其形式如下：
[0079][0080]
在采用梯度下降法优化模型参数时，需要最小化代价函数j(θ)，其表达式为：
[0081][0082]
式中，λ＞0，项为权重衰减项，该项会惩罚过大的参数值，引入该项后代价函数j(θ)就变成了严格的凸函数，可保证有唯一解；
[0083]
代价函数j(θ)的导数表达式为：
[0084][0085]
式中，本身是一个向量，它的第一个元素是j(θ)对θ
j
的第l个分量的偏导数。
[0086]
利用代价函数j(θ)的偏导数采用梯度下降法即可最小化j(θ)；
[0087]
即可输出故障的概率值。
[0088]
本发明的特征在于将小波包变换和gru型长短时记忆神经网络相结合，利用小波包变换处理复杂的飞线性、非平稳的风电机组滚动轴承的振动信号的优势，以及gru型长短时记忆神经可以有效解决传统rnn网络处理具有长时间依赖关系的信号时所存在的梯度消失问题，并且gru型长短时记忆神经网络与标准的lstm神经网络模型更简单，训练速度更快，且适合处理较大规模数据。
[0089]
本文案例中所使用的gru型lstm神经网络的组成含有两层隐藏层，每层隐藏层包含有200个gru记忆模块。模型输入是小波包变换提取出的一个8维的风电机组轴承故障的特征矢量，第一层隐含层的输出是第二层隐含层的输入，输出层是由四个softmax多分类单元组成的，对应4位的故障编码，其输出单元的意义如表1所示。选取了北方某风电场相同型号1.5mw的4台风电机组的滚动轴承振动信号作为样本数据，可将其分成两部分：训练与测
试数据。利用小波包变换后，并得出各频带上的能量特征从而构成样本的特征矢量。其中，训练数据长度为24576的序列，测试数据是长度为8192的序列。故障诊断结果见表2。
[0090]
表1输出单元的意义
[0091]
输出单元c1输出单元c2输出单元c3输出单元c4意义1000滚动体剥落0100内圈剥落0010外圈剥落0001正常
[0092]
表2诊断结果
[0093][0094]
由输出结果看出，诊断的最终结果与风电机组滚动轴承所发生的故障类型一致。