一种用于介质电性研究的计算方法、可读介质及设备与流程

本发明涉及地球物理勘探、岩石物理实验技术领域，具体涉及一种用于介质电性研究的计算方法、可读介质及设备。

背景技术：

在岩石物理、电磁勘探中，常常需要用合适的电模型把岩石(或其他孔隙固体)的宏观电性(电导率、介电常数)与岩石的岩性参数(孔隙度、饱和度、水含量)联系起来，以便于得到石油、地下水或金属矿体的具体含量。同时在材料科学中，混凝土的延迟力学行为和耐久性能也都取决于其含水量。而水含量与孔隙度息息相关，因此，评估孔隙度对于土木工程结构和岩石勘探至关重要。

但是现有的电分析模型都有一定的局限性，并不能适用于所有情况。

landauer基于有效介质理论，提出了一种混合介质的混合介电常数公式。但是此公式假设所有的介质都是由球形颗粒堆积而成，当介质的微观结构分布和均匀分布差距较大的时候，使用此公式会有较大的误差。

现在常用的岩电模型都存在一定的问题。最常用的阿尔奇公式是一个经验公式，并没有理论的推导过程，且无法应用于泥质含量较高的岩石中；同时存在一些对阿尔奇公式进行修正了的模型，这些模型参数复杂，只适用一些特定的情况；除此之外，基于理论推导的maxwell-garnettequation、bruggemanself-consistenteffectivemediumapproximation和jaysundere-smithequation公式，以及他们的一系列衍生公式则需要混合介质中存在某一相完全离散，且体积分数至少<0.5。

总的来说，现有的岩电模型都有一定的局限性，没有一种现有的模型能适用于所有的混合电性的情况。而本发明寻找到了一种适用于任何体积分数、任何微观形态分布的岩电模型，可以广泛应用于大部分情况。

技术实现要素：

本发明提出的一种用于介质电性研究的计算方法，具体涉及孔隙介质孔隙度或含水量的求得方法，可解决勘探、材料问题中求取孔隙介质水含量的问题。

为实现上述目的，本发明采用了以下技术方案：

一种用于介质电性研究的计算方法，包括以下步骤：

s100、测量介质中流体相的介电常数，及测量介质骨架的介电常数；

s200、测量样品在不同孔隙度，水饱和度或其他变化情况下的整体介电常数；

s300、推导骨架和流体的介电常数、含水量与整体介电常数的规律关系式；

s400、利用s300所求的关系式，对s100与s200的数据进行分析，求得介质性质参数。

进一步的，所述s300具体包括：

首先通过逐级递推单独不规则颗粒在均匀空间中的极化情况，然后通过有效介质理论，把多相介质的每一个颗粒，都看作是存在于全空间的有效介质体中的一个小颗粒；

则宏观来说，全空间尺度下并不会有极化强度和激发极化场，即把所有颗粒的极化强度求和之后，值应该和为0，最终得到：

即为求得的规律，其中εi为介质每一相的介电常数，fi为每一相体积百分比，<li>为参数，表示介质形状分布，εm为介质的混合介电常数。

进一步的，所述s100具体包括：

使用开放式同轴探针测量介质中流体相的介电常数；

在固体表面不同位置进行多次测量，得到介质骨架的介电常数。

进一步的，所述s100、s200及s300中介电常数换成电导率同样成立。

另一方面，本发明还公开一种计算机可读存储介质，存储有计算机程序，所述计算机程序被处理器执行时，使得所述处理器执行上述方法的s400的步骤。

第三方面，本发明还公开一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，所述计算机程序被所述处理器执行时，使得所述处理器执行上述方法的s400步骤。

由上述技术方案可知，本发明的用于介质电性研究的计算方法，通过新的电学分析模式得到了新的电学规律，利用新的规律去分析测量的介电常数数据。本发明可适用于任何体积分数、任何微观形态分布的孔隙介质，可以广泛应用于大部分勘探、材料的情况。参数相较其他模型较少，在全孔隙度范围具有普适性，在样本孔隙度跨度较大的情况下依旧适用，适用于三相及更多相介质，其他的岩电模型需要额外的修正才能适用于多相介质。本发明不需要任何修正就可以适用于大部分条件，可以得到比以往方法更好的介质性质参数等结果。

附图说明

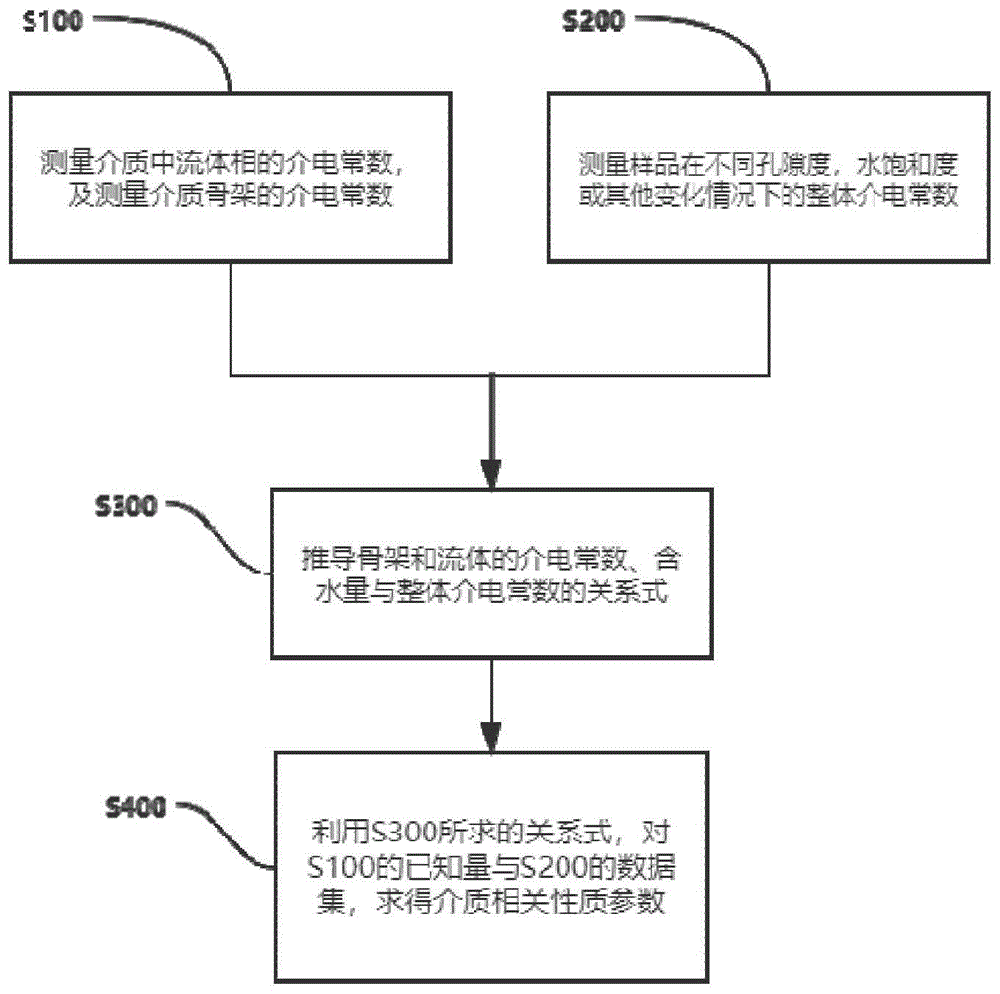
图1是本发明的方法流程图；

图2是本发明的s300分析中的示意图；

图3是本发明实施例1中含水量与整体介电常数的数据图；

图4是本发明实施例1的结果分析对比图；

图5是本发明实施例2的结果分析对比图。

具体实施方式

为使本发明实施例的目的、技术方案和优点更加清楚，下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例是本发明一部分实施例，而不是全部的实施例。

如1所示，本发明实施例的一种用于介质电性研究的计算方法，包括以下步骤：

s100、测量介质中流体相的介电常数，及测量介质骨架的介电常数；

s200、测量样品在不同孔隙度，水饱和度或其他变化情况下的整体介电常数；

s300、推导骨架和流体的介电常数、含水量与整体介电常数的规律关系式；

s400、利用s300所求的关系式，对s100与s200的数据进行分析，求得介质性质参数。

以下具体说明：

s100、对于研究目标，首先使用开放式同轴探针(或其他仪器)测量介质中流体相的介电常数(也可以是电导率)。然后测量介质骨架的介电常数(电导率)，在固体表面不同位置进行多次测量。得到介质骨架的介电常数(电导率)。

s200、得到s100的值后，改变其他条件来扩充需要的数据集。在介质中填充不同量的流体，或改变样品的孔隙度，利用开放式同轴探针(或其他仪器)测量不同水饱和度情况下的整体介电常数(电导率)。得到整体介电常数(电导率)的变化关系；

s300、推导在一般情况下，s100数据与s200数据的变化规律，骨架和流体的介电常数、含水量与整体介电常数的关系。首先如图2，研究一个单独的颗粒在均匀全空间的情况。颗粒的介电常数为ε1。其外部均匀全空间介电常数为εm，外场为e0。问题为求一个颗粒的极化强度。

颗粒的极化强度和电场互相激发最终达到一个稳定状态，但直接求取颗粒极化强度的方法无法适用于不规则的颗粒，所以用递推的思路求取颗粒的总极化强度。首先考虑极化所产生的电场变化还没有发生，考虑没有变化的外场e0所产生的极化强度，称之为第1级极化强度p1，再考虑第1级极化强度p1所产生的极化电场，称之为第1级激发极化场，之后依次递推第2级、第3级、……直到第n级极化强度与激发极化场。在这个假设下，注意这时候并不是电学稳定的状态，所以一些电学推论不成立。因为没有极化电场的影响，极化电荷会均匀的分布在颗粒表面，与无限大介质板的情况类似，电极化强度为界面的极化电荷密度。此时颗粒内外的电场都还没有变化，都为起始的外场e0。此电场在颗粒表面产生的极化电荷为内外电场产生的感应电荷的综合，即：

p1＝εme0-ε1e0＝(εm-ε1)e0(1)

对于极化强度所产生的激发极化场，可以类比退极化场的推导过程，加入一个类似退极化因子参数〈l1〉，得到：

这是第1级极化强度与激发极化场的推导，之后每一级的极化强度与激发极化场都是由上一级的极化强度与激发极化场产生，有递推的规律。得到递推公式：

其中p1为外场e0对应的极化强度；en为第n级激发极化场；pn为第n级极化强度。<l1>为颗粒的形状相关的参数，类似退极化因子，只与颗粒形状有关。化简得到pn的表达式为：

这是每一级的极化强度，关心的是颗粒的总极化强度，所以对n进行求和，得到颗粒的总极化强度p为:

以上为均匀空间的一个不规则颗粒的极化情况。对于多相介质来说，求取混合介电常数的问题可以转化为：寻找一种均匀介质，此介质在宏观上的电学性质与多相介质表现一样，它的介电常数就是所求的混合介电常数。这就是有效介质理论的核心思想。这个均匀介质称之为多相介质的有效介质。在此想法上引申，可以把多相介质的每一个颗粒，都看作是存在于全空间的有效介质体中的一个小颗粒。而宏观来说，全空间尺度下并不会有极化强度和激发极化场，即把所有颗粒的极化强度求和之后，值应该和为0，即：

式中j为颗粒编号。对于多相介质来说，可以用颗粒所属的介质种类重新分类，设i为介质种类编号，fi为第i种介质所占体积百分比，得:

即为求得的规律。使得把介质每一相的介电常数εi、体积百分比fi、介质形状〈li〉与介质的混合介电常数εm直接联系了起来。而混合介质的电导率与介电常数的规律相同，即电导率可以直接使用这里得到的介电常数的关系式。

s400、对s100与s200的测量结果，利用s300所求得的规律进行分析，求得所关注的介质性质(孔隙度、饱和度或孔隙分布情况等)。

具体可根据实际需要进行更细致的分析。如果是材料问题，根据s400所得的介质性质就可以进行后续的含水量与其他材料物性(受力变化、耐久损耗等等)联系进行更好的研究；如果是勘探问题，s400所得的孔隙度、饱和度等信息对后续的地质研究，矿藏或地下水开采有着重要的指示意义。

以下为两个具体的实例：

1：对于实验室材料研究：以水填充的非饱和沙为例，介电常数是用于估算材料水含量的主要属性。首先使用开放式同轴探针测量所使用的水的介电常数，得到介电常数为80。然后测量沙的介电常数，在固体表面不同位置进行了五次测量。得到的介电常数平均值为4.5，标准差等于0.1。即为已知沙和水介电常数情况下，含水量与整体介电常数的关系。在沙中填充不同量的水，通过体积换算得到饱和度；利用开放式同轴探针测量不同水饱和度情况下的整体介电常数实部，数据如图3所示，十字代表数据的误差。利用整体介电常数与含水量的关系，求得本研究方法得到的含水量。为了方便与其他方法对比，在图4中也展示了其他方法得到的结果。其中粗黑线为本专利的方法，其他点与线为其他方法。可以看到本方法得到的含水量与实际的最为贴近。后续可以利用求得的含水量，对沙水混合材料的延迟力学行为和耐久性能与含水量的关系进行研究，得到更加贴近实际关系的数据。

2：对于地下地质勘察：地下的孔隙度分布是地质最关心的问题之一。首先在目标区域进行岩石采样与地下水采样，把样本在实验室进行分析，了解目标区域的的岩石骨架电导率与地下水的电导率的情况。即为已知岩石骨架和水电导率情况下，孔隙度与地层因子(地层因子＝地下水电导率/整体电导率)的关系。利用仪器测量不同孔隙度情况下的整体电导率，数据如图5所示。之后得到整体介电常数与含水量的关系。为了方便与其他方法对比，在图5中也展示了其他方法得到的结果。可以看到本方法得到的关系与实际的关系走向最为贴近。后续对所关注的目标区域进行高密度电法勘探，可以得到区域的地层因子分布图，利用所求得的关系，得到地下的孔隙度随不同位置的分布图。此孔隙度分布图对此区域的地质研究有重要的意义。

综和之上两个实例所展示，本发明寻找到了一种适用于任何体积分数、任何孔隙形态分布的分析技术，可以广泛应用于大部分情况，可以准确的得到所需要的介质性质。由于推导没有任何近似、忽略的过程，所以本方法具有优秀的普适性，在样本孔隙度跨度较大、或其他特殊的情况下依旧适用，甚至可以适用于三相及更多相介质。而其他的岩电模型需要额外的修正或修改之后才能适用于多相介质。而这几点对于实际的复杂地质情况或者孔隙材料十分重要。

另一方面，本发明实施例还公开一种计算机可读存储介质，存储有计算机程序，所述计算机程序被处理器执行时，使得所述处理器执行上述方法的s400的步骤。

第三方面，本发明实施例还公开一种计算机设备，包括存储器和处理器，所述存储器存储有计算机程序，所述计算机程序被所述处理器执行时，使得所述处理器执行上述方法的s400步骤。

本领域内的技术人员应明白，本申请的实施例可提供为方法、系统、或计算机程序产品。因此，本申请可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本申请可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。

本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。

这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。

这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。

以上实施例仅用以说明本发明的技术方案，而非对其限制；尽管参照前述实施例对本发明进行了详细的说明，本领域的普通技术人员应当理解：其依然可以对前述各实施例所记载的技术方案进行修改，或者对其中部分技术特征进行等同替换；而这些修改或者替换，并不使相应技术方案的本质脱离本发明各实施例技术方案的精神和范围。