一种面向环境参数空间的流形建模方法

1.本发明涉及环境仿真与机器学习技术领域，特别提供了一种面向环境参数 空间的流形建模方法。


背景技术：

2.根据真实环境中的太阳光照、平均温度、风速、降雨量、空气相对湿度、 经度、维度等环境参数信息，由于各种参数之间存在着客观物理中的某些联系， 如地理位置(精度及维度)影响太阳光照，区域的光照强度影响该地区的地表 温度，降雨量影响着空气相对湿度等等，直接在欧氏空间中对真实环境中的诸 多参数进行建模，可能会导致以下问题：
3.(1)由于欧氏空间中的各坐标相互正交，若直接在欧氏空间中进行建 模，也就是假设真实环境中的各个参数之间是互斥的(不相关的)。显而易见， 这一假设与实际参数之间的联系不符。
4.(2)真实环境中的参数众多，为了提高环境参数模型的可靠性和准确 性，若对所有参数均进行建模，则参数空间的维数可能过高，计算量复杂。
5.针对以上问题，根据环境参数之间的相互联系，利用非欧几何中的流形空 间，构建真实场景环境参数空间中的几何模型，对仿真模型中的环境参数提供 相应的执置信度评价结果。


技术实现要素：

6.鉴于此，本发明的目的在于提供一种面向环境参数空间的流形建模方法，以 解决深度网络可解释性问题。
7.本发明提供的技术方案是：一种面向环境参数空间的流形建模方法，包括 以下步骤：
8.1)将候选地区的环境参数数据进行预处理，建立该地区环境参数的数值空 间模型；
9.2)利用黎曼流形的几何结构与空间特性，构建环境数值参数对应的流形空 间表征；
10.3)根据候选地区在不同时间下的流形空间位置，对仿真参数进行流形空间 表征；
11.4)对仿真参数进行流形空间表征并计算其对应的测地线距离，输出环境仿 真参数与该地历史环境参数在流形空间中的测地线距离；
12.5)结合环境仿真参数在流形空间中的测地线距离，最终对环境仿真参数的 可靠性进行评估。
13.所述建立该地区环境参数的数值空间模型，包括以下步骤：
14.对于候选地区，环境数据库中包含n天的环境参数样本，即该地区的环境 参数样本空间表示为a＝{v1,v2,
…
,vn}，其中vi代表该地区 不同时期实测的d维环境参数数据向量，包含风速、温度、高度、光照。
15.所述利用黎曼流形的几何结构与空间特性，构建环境数值参数对应的流形 空间表征，具体通过协方差矩阵来对实测的真实环境数据进行流形表征。
16.所述根据候选地区在不同时间下的流形空间位置，对仿真参数进行流形空 间表征，包括以下步骤：
17.通过仿真，得到候选地区不同时期的d维环境参数数据向量；
18.通过协方差矩阵来对仿真参数的环境数据进行流形表征。
19.所述协方差矩阵通过下式得到：
20.构建协方差矩阵空间xr：
[0021][0022]
其中，vi表示不同时期的d维环境参数数据向量，ur为对应均值；
[0023][0024]
所述输出环境仿真参数与该地历史环境参数在流形空间中的测地线距离， 包括以下步骤：
[0025]
仿真数据在流形空间中与实测的真实数据参考点的测地线距离：
[0026][0027]
式中x,y分别为仿真参数数据与实测的真实环境数据协方差矩阵上的任意 两点，trace(
·
)表示矩阵的迹，log(
·
)表示矩阵的对数函数。
[0028]
所述结合环境仿真参数在流形空间中的测地线距离，最终对环境仿真参数 的可靠性进行评估，包括以下步骤：
[0029]
设置可信度阈值为τ；
[0030]
若仿真数据在流形空间中与实测的真实数据参考点的测地线距离 d(x,y)≤τ，则认为所得到的仿真环境参数具有较高的可靠性；否则，认为所 得到的仿真环境参数具有较低的可靠性。
[0031]
所述环境参数数据包含风速、温度、高度、光照。
[0032]
本发明提供的一种面向环境参数空间的流形建模方法，有益效果如下：
[0033]
利用黎曼流形的几何结构与空间特性，构建环境数值参数对应的流形空间 表征，对固定地点在不同时间下的流形空间位置进行定义，通过对仿真参数进 行流形空间表征并计算其对应的测地线距离，输出环境仿真参数与该地历史环 境参数在流形空间中的测地线距离，利用黎曼流形的几何表征方法，能够有效 降低原始高维参数空间中的计算量，结合参数间的耦合关系，提高模型的计算 能力，最终对环境仿真参数的可靠性进行评估。
附图说明
[0034]
下面结合附图及实施方式对本发明作进一步详细的说明：
[0035]
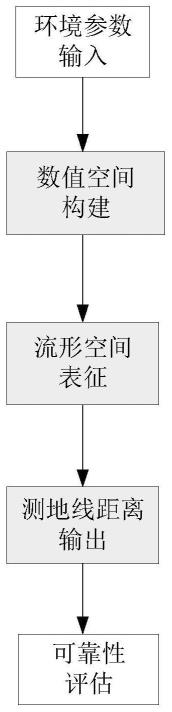
图1为本发明提供的一种面向环境参数空间的流形建模方法流程示意图；
[0036]
图2为本发明提供的一种面向环境参数空间的流形建模方法中环境参数数 据样
本图。
[0037]
图3为本发明提供的一种面向环境参数空间的流形建模方法中环境参数的 流形表征图。
[0038]
图4为仿真环境参数数据的测地线距离计算结果图。
具体实施方式
[0039]
下面将结合具体的实施方案对本发明进行进一步的解释，但并不局限本发 明。
[0040]
本发明公开了一种面向环境参数空间的流形建模方法，方法流程包括：环 境参数输入、数值空间构建、流形空间表征、测地线距离输出、仿真参数可靠 性评估共五个部分。本发明首先对环境参数进行数值空间建模，对于固定地区 的大量环境数据，建立该地区环境参数的数值空间模型；
[0041]
之后，利用黎曼流形的几何结构与空间特性，构建环境数值参数对应的流 形空间表征，对固定地点在不同时间下的流形空间位置进行定义，通过对仿真 参数进行流形空间表征并计算其对应的测地线距离，输出环境仿真参数与该地 历史环境参数在流形空间中的测地线距离，最终对环境仿真参数的可靠性进行 评估。
[0042]
本发明针对环境参数的大量历史数据，有效利用数据的几何结构，对环境 参数的数值空间进行流形建模，对于仿真生成的环境仿真参数数据，通过计算 环境参数在流形空间中的测地线距离，提供了一种环境仿真参数可靠性的评估 方法。
[0043]
一种面向环境参数空间的流形建模方法，包括：
[0044]
步骤一，输入环境参数数据。
[0045]
步骤二，对输入的环境参数数据进行预处理，对于固定地区的大量环境数 据，建立该地区环境参数的数值空间模型。
[0046]
步骤三，构建环境数值参数对应的流形空间表征。
[0047]
步骤四，对固定地点在不同时间下的流形空间位置进行定义，对仿真参数 进行流形空间表征。
[0048]
步骤五，对仿真参数进行流形空间表征并计算其对应的测地线距离。
[0049]
步骤六，输出环境仿真参数与该地历史环境参数在流形空间中的测地线距 离，结合环境仿真参数在流形空间中的测地线距离，最终对环境仿真参数的可 靠性进行评估。
[0050]
所述步骤二对输入的环境参数数据进行预处理，建立该地区环境参数的数 值空间模型，实现参数空间建模中包括如下步骤：
[0051]
步骤2-1，对于真实空间中的环境参数模型，选取固定地区某年的实测环境 数据作为构建环境参数模型的相关数据库。
[0052]
步骤2-2，以固定地区的每天数据为单位，构建样本数据，并筛除某些无效 数据。
[0053]
步骤2-3，对于固定地区而言，对应的大量环境数据库中包含n天的环境参 数样本，即该地区的环境参数样本空间可表示为a＝{v1,v2,
…
,vn}，其中}，其中vi代表该地区每天实测的d维环境参数数据向量，包含风速、温度、 高度、光照等因素。
[0054]
如图2所示的桃仙机场5月真实环境实测数据。对于真实空间中的环境参 数模型，选取辽宁省沈阳市桃仙机场2019年的实测环境数据作为构建环境参数 模型的相关数据库，其中包含参数如下：
[0055]
1)站名；
[0056]
2)站点号；
[0057]
3)日期；
[0058]
4)平均风速(knots)；
[0059]
5)最大持续风速(knots)；
[0060]
6)最大瞬时风速(knots)；
[0061]
7)纬度，经度；
[0062]
8)能见度(mi)；
[0063]
9)降水量(in)；
[0064]
10)露点温度(f)；
[0065]
11)高度(m)；
[0066]
12)平均气温(℃)，日最高气温(℃)，日最低气温(℃)；
[0067]
13)平均相对湿度(％)，最小相对湿度(％)；
[0068]
14)小型蒸发量(mm)；
[0069]
15)平均本站气压(hpa)，日最高本站气压(hpa)，日最低本站气压(hpa)。
[0070]
桃仙机场的环境实测数据如图2所示，其中以每天数据为单位，共包含2019 年的365条数据。该数据来源自官方气象网站，筛除某些无效数据后，共计360 条数据。
[0071]
所述步骤三中包括利用黎曼流形的几何结构与空间特性，构建环境数值参 数对应的流形空间表征。
[0072]
由于获取的实测数据形式为向量形式，构建真实环境数据的流形空间，其 关键问题是如何将向量数据表征在流形空间中。对于环境参数的流形表征，本 专利采用正定对称流形表示方法将实测的环境参数表征在黎曼流形空间。采用 正定对称流形结构建立环境空间模型的理由如下：
[0073]
由于真实环境空间的参数众多，正定对称流形的维度仅与参数的本征维度 有关，与环境参数的数据数量无关，即建立的流形环境参数模型复杂度不受实 测数据的数据量影响。
[0074]
通过协方差矩阵来对实测的真实环境数据进行流形表征。对于不同时期的 历史环境数据，计算其环境参数相关性，构建协方差矩阵空间。
[0075]
所述步骤四包括使用正定对称流形对环境参数进行表征。
[0076]
协方差矩阵在目标分类、目标检测与目标跟踪方面展现出良好的可适用性， 图像的协方差矩阵能够表征出图像区域内每个不同特征维度之间关系。对于环 境参数数据而言，协方差矩阵能够表示出每个环境参数维度之间的相互关系。 因此，对于桃仙机场2019年的360条实测环境参数数据，按照12个月份，每 个月份分别对应构建出由该月的30天实测环境数据组成的月份环境参数矩阵。 一年中12个月份的对应协方差矩阵计算结果如图3所示。
[0077]
所述步骤五包括对仿真参数进行流形空间表征并计算其对应的测地线距离。 通过对仿真参数在正定对称流形空间中进行表征，使用欧氏对数黎曼距离公式， 计算环境仿真参数与该地历史环境参数在流形空间中的测地线距离
[0078]
所述步骤六包括基于环境仿真参数在流形空间中的测地线距离，设置阈值 参数，
判断阈值参数与所计算得到的测地线距离的关系，对环境仿真参数的可 靠性进行评估。
[0079]
如图1所示，本发明提供了一种面向环境参数空间的流形建模方法，包括如 下步骤：
[0080]
步骤一：输入环境参数数据，将环境参数数据向量化表示。实际中，判断 数据的相关性与有效性，选择相关性低的环境因素。
[0081]
步骤二，建立环境参数的数值空间模型。对于真实空间中的环境参数模型， 选取固定地区某年的实测环境数据作为构建环境参数模型的相关数据库。以固 定地区的每天数据为单位，构建样本数据，并筛除某些无效数据。对于固定地 区而言，对应的大量环境数据库中包含n天的环境参数样本，即该地区的环境 参数样本空间可表示为
[0082]
a＝{v1,v2,
…
,vn}，
[0083]
其中vi代表该地区每天实测的d维环境参数数据向量，包 含风速、温度、高度、光照等因素。
[0084]
步骤三，通过协方差矩阵来对实测的真实环境数据进行流形表征。对于不 同时期的历史环境数据，计算其环境参数相关性，构建协方差矩阵空间：
[0085][0086]
其中vi表示不同时期的环境参数历史实测数据，ur为对应均值。ur的计算公式 为：
[0087][0088]
步骤四，使用正定对称流形对环境参数数据进行流形空间表征。协方差矩 阵在目标分类、目标检测与目标跟踪方面展现出良好的可适用性，图像的协方 差矩阵能够表征出图像区域内每个不同特征维度之间关系。类似地，对于环境 参数数据而言，协方差矩阵能够表示出每个环境参数维度之间的相互关系。因 此，对于桃仙机场2019年的360条实测环境参数数据，按照12个月份，每个 月份分别对应构建出由该月的30天实测环境数据组成的月份环境参数矩阵。如 图3所示的桃仙机场2019年真实环境实测数据流形表征。
[0089]
步骤五，通过对仿真参数进行流形空间表征并计算其对应的测地线距离， 输出环境仿真参数与该地历史环境参数在流形空间中的测地线距离，包括以下 步骤：
[0090]
计算仿真参数数据在流形空间中与黎曼几何中心的测地线距离：
[0091][0092]
式中x,y表示正定对称流形上的任意两点，trace(
·
)表示矩阵的迹，log(
·
)表 示矩阵的对数函数。
[0093]
步骤六，测试的仿真数据主要分成两类：一类为合理的仿真数据，根据某 一月份实测真实环境数据为参考获得；另一类为不合理的仿真数据，以此来测 试环境参数流形空间模型的有效性。
[0094]
将计算得出的5月份正定对称流形矩阵作为流形参数空间中的真实数据参 考点，分别对仿真测试数据进行测试，计算仿真数据在流形空间中与各月份真 实数据参考点的测地线距离，最终计算得出的流形测地线距离作为评价仿真参 数可靠性与合理性的判别
依据。
[0095]
具体而言，设置可信度阈值为τ，若计算得出仿真数据在流形空间中与各 月份真实数据参考点的测地线距离d(x,y)≤τ，则认为所得到的仿真环境参数 具有较高的可靠性；否则，若计算得出仿真数据在流形空间中与各月份真实数 据参考点的测地线距离d(x,y)＞τ，则认为所得到的仿真环境参数具有较低的 可靠性。
[0096]
本发明提出的一种面向环境参数空间的流形建模方法所使用的样本库示意 图如图2所示，实验测试结果如图3所示。
[0097]
实验测试的仿真数据主要分成两类：一类为合理的仿真数据，根据某一月 份实测真实环境数据为参考获得；另一类为不合理的仿真数据，以此来测试环 境参数流形空间模型的有效性。
[0098]
实验结果如下：
[0099]
(1)当测试数据为合理的仿真数据时，选取桃仙机场的5月份实测环 境参数数据为参考，生成6组可能的合理仿真环境参数，计算其与该月流形参 考点的测地线距离，若小于阈值，即认定仿真参数合理；
[0100]
(2)类似地，对于不合理的仿真参数数据，计算其与该月流形参考点 的测地线距离，若大于阈值，即认定仿真参数为不合理；
[0101]
对于两类仿真环境参数数据的计算结果如图4所示，其中，一类仿真数据 的距离值为9.7051，而二类仿真数据的距离值为58.8508，输出结果为第一类数 据为合理，第二类数据为不合理数据，验证了此模型的有效性。
[0102]
上面结合附图对本发明的实施方式做了详细说明，但是本发明并不限于上 述实施方式，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本 发明宗旨的前提下作出各种变化。