一种考虑尾流效应的风电场布局优化方法

本发明涉及风电领域，具体涉及一种考虑尾流效应的风电场布局优化方法。

背景技术：

在现代风电场的设计规划中，往往将几十台风电机组依照一定规律排列。当间距和排列方式不合理时，尾流效应就会大大影响发电效率。风轮后尾流区的产生，是由于气流通过上游的风电机风轮后湍流强度会增加、风速会降低。尾流区的尾流效应主要从两个方面影响风电机组：首先是尾流区风速降低会造成尾流区内风电机组发电量损失。其次是湍流强度的增加，其影响风电机组的疲劳载荷和气动性能。国外研究表明，完全工作在尾流环境中的风电机组效率损失最高能达10％～20％。因此，开展风电场尾流计算方法的研究继而优化风电机排布方式，实现风电机效率最大化具有重要的学术价值和经济效益。

技术实现要素：

发明目的：本发明的目的是提供解决多重尾流效应下风电场布局问题的一种新的优化方法。

技术方案：本发明提供的一种考虑尾流效应的风电场布局优化方法，用于获取目标风电场中风电机的最优排布方案，目标风电场为地形平坦的正方形区域，且目标风电场中的各风电机的风轮尺寸彼此相等，各风电机的发电效率η彼此相等；方法包括如下步骤：

步骤1：基于吹入目标风电场中的自然风速v、风电机的数量n，以及各个风电机的发电效率η，构建目标风电场中各风电机在预设时间段t内的发电量之和模型ptotal(v,n,η,t)：

基于风电机的数量n，构建各个风电机的成本之和模型cost(n)：

将各个风电机的成本之和模型cost(n)和各个风电机在预设时间段t内的发电量之和模型ptotal(v,n,η,t)的比作为目标函数；

步骤2：以风电场的大小和风电机安装的最小间距为约束条件，获取一组风电机数量，进而获取一组与各风电机数量相对应的预设风电机排布方案；

步骤3：采集吹入目标风电场中的自然风速v，根据各个风电机排布方案，基于遗传算法，应用目标函数获取与各个风电机排布方案所对应的目标函数值，将目标函数值最小的风电机排布方案作为目标风电场中风电机的最优排布方案。

作为本发明的一种优选方案，在步骤1中，所述目标风电场中各风电机在预设时间段t内的发电量之和模型ptotal(v,n,η,t)为：

其中，r为风电机的风轮半径，ρ为风电机所处区域的空气密度，vi为第i个风电机的输入风速，i＝1,2...n；v为不考虑尾流影响时风电机i的输入风速；各风电机的风轮所在平面与吹入目标风电场中的自然风的风向相垂至，βki为风电机i的上游的第k个风电机在风电机i处的投影面积ash与风电机i的风轮外周构成的圆形区域面积的比值，所述第k个风电机在风电机i处的投影为：风电机i的上游的第k个风电机的各风轮外周构成的圆形区域沿着吹入目标风电场中的自然风的风向在风电机i的风轮所在平面的垂直投影；vw-ki为第k个风电机的尾流区在第i个风电机处的风速。

作为本发明的一种优选方案，在步骤2中，构建的风电机排布模型为：

目标风电场中电机的数量n的算数平方根为n，n为整数；

将目标风电场等分为n行n列，进而获取n×n个面积相等的正方形子区域，各风电机与各正方向子区域一一对应设置，各风电机分别位于对应正方形子区域的中心点处；各风电机的风轮所在平面与吹入目标风电场中的自然风的风向相垂直。

作为本发明的一种优选方案，各风电机的风轮中心位于同一水平面上，风电机i的上游的第k个风电机在风电机i处的投影面积ash的方法包括如下步骤：

步骤a：获取风电机i的上游的第k个风电机的风轮中心和风电机i的风轮中心的距离d，风电机i的上游的第k个风电机的风轮中心距离该两个风电机的投影交接处的水平距离d1；

步骤b：若d1满足条件：r3<d1<r3+r，根据如下公式：

获取风电机i的上游的第k个风电机在风电机i处的投影面积ash；

其中，r3为风电机i的上游的第k个风电机的风轮半径，r为风电机i的风轮半径，z为该两个风电机中任一风电机的风轮中心距离该两个风电机的投影交接处的垂直距离；

若d1满足条件：r3-r<d1<r3，根据如下公式：

获取风电机i的上游的第k个风电机在风电机i处的投影面积ash。

作为本发明的一种优选方案，方法还包括如下步骤：

步骤a-1：以沿着吹入目标风电场中的自然风风向的轴为x轴，以垂直于风电场平面的轴为y轴建立空间坐标系xoy；获取在该空间坐标系xoy中，风电机i的上游的第k个风电机的风轮中心的坐标(xk,yk)，以及风电机i的风轮中心的坐标(xi,yi)；

步骤a-2：分别根据如下公式：

d＝|xk-xi|

获取风电机i的上游的第k个风电机的风轮中心和风电机i的风轮中心的距离d、风电机i的上游的第k个风电机的风轮中心距离该两个风电机的投影交接处的水平距离d1，以及该两个风电机中任一风电机的风轮中心距离该两个风电机的投影交接处的垂直距离z。

作为本发明的一种优选方案，在步骤1中，各个风电机的成本之和模型cost(n)为：

其中，n为目标风电场中风电机的数量。

有益效果：本发明公开了一种考虑尾流效应的基于遗传算法的风电场布局优化方法，通过构建发电量之和模型和成本之和模型，基于该两个模型获取目标函数，并基于遗传算法获取目标函数值最小的风电机排布方案，方法简单且处理速度快。

附图说明

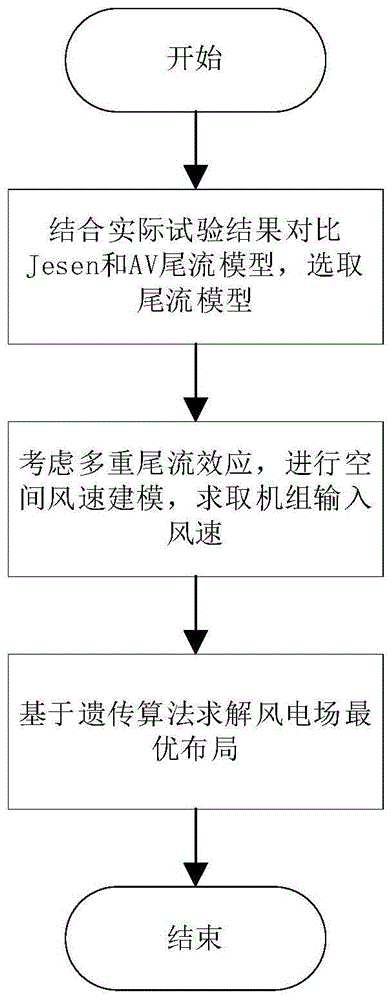
图1为本发明提供的的方法流程图；

图2为本发明实施例提供的一种风电机组尾流部分遮挡情况示意图；

图3为本发明实施例提供的另一种风电机组尾流部分遮挡情况示意图；

图4为本发明实施例提供的坐标变换示意图；

图5为本发明实施例提供的计算多重尾流效应下获取风电机组的输入风速的框图；

图6为本发明实施例提供的一种风电场离散图；

图7为本发明实施例提供的另一种风电场离散图；

图8为本发明实施例提供的一种风况的示意图；

图9为本发明实施例提供的另一种风况的示意图。

具体实施方式

下面结合附图对本发明作进一步描述。以下实施例仅用于更加清楚地说明本发明的技术方案，而不能以此来限制本发明的保护范围。

参照图1，本发明提供的方法包括如下步骤：

结合实际试验结果和实验数据，从jesen尾流模型和av尾流模型中选取av尾流模型进行输入风速计算，在计算时考虑多重尾流效应，获取各风电机的输入风速，基于遗传算法求解目标风电场中各风电机的最优布局。

本方案适用于地形平坦的正方形目标风电场区域，目标风电场中的各风电机的风轮尺寸彼此相等，各风电机的发电效率η彼此相等。

风电场布局优化方法包括如下步骤：

步骤1：基于吹入目标风电场中的自然风速v、风电机的数量n，以及各个风电机的发电效率η，构建目标风电场中各风电机在预设时间段t内的发电量之和模型ptotal(v,n,η,t)。

考虑尾流叠加效应，根据如下公式：

获取风电机i的输入风速vi，i＝1,2...n；

其中，v为不考虑尾流影响时风电机i的输入风速；βki为风电机i的上游的第k个风电机在风电机i处的投影面积ash与风电机i的风轮外周构成的圆形区域面积的比值，所述第k个风电机在风电机i处的投影为：风电机i的上游的第k个风电机的各风轮外周构成的圆形区域沿着吹入目标风电场中的自然风的风向在风电机i的风轮所在平面的垂直投影；vw-ki为第k个风电机的尾流区在第i个风电机处的风速。

根据如下公式：

获取第k个风电机的尾流区在风电机i处的风速vw-ki。

在本方案中，各风电机的风轮中心位于同一水平面上，风电机i的上游的第k个风电机在风电机i处的投影面积ash的方法包括如下步骤：

步骤a：获取风电机i的上游的第k个风电机的风轮中心和风电机i的风轮中心的距离d，风电机i的上游的第k个风电机的风轮中心距离该两个风电机的投影交接处的水平距离d1。

步骤b：若d1满足条件：r3<d1<r3+r，根据如下公式：

获取风电机i的上游的第k个风电机在风电机i处的投影面积ash；

其中，r3为风电机i的上游的第k个风电机的风轮半径，r为风电机i的风轮半径，z为该两个风电机中任一风电机的风轮中心距离该两个风电机的投影交接处的垂直距离；

若d1满足条件：r3-r<d1<r3，根据如下公式：

获取风电机i的上游的第k个风电机在风电机i处的投影面积ash。

两种不同情况的风电机的示意图如图2和图3所示。

具体的，根据步骤a-1至步骤a-2获取风电机i的上游的第k个风电机的风轮中心和风电机i的风轮中心的距离d、风电机i的上游的第k个风电机的风轮中心距离该两个风电机的投影交接处的水平距离d1，以及该两个风电机中任一风电机的风轮中心距离该两个风电机的投影交接处的垂直距离z：

步骤a-1：以吹入目标风电场中的自然风的风向为x轴的正方向，以垂直于风电场平面的轴为y轴建立空间坐标系xoy；获取在该空间坐标系xoy中，风电机i的上游的第k个风电机的风轮中心的坐标(xk,yk)，以及风电机i的风轮中心的坐标(xi,yi)；

步骤a-2：分别根据如下公式：

d＝|xk-xi|

获取风电机i的上游的第k个风电机的风轮中心和风电机i的风轮中心的距离d、风电机i的上游的第k个风电机的风轮中心距离该两个风电机的投影交接处的水平距离d1，以及该两个风电机中任一风电机的风轮中心距离该两个风电机的投影交接处的垂直距离z。

目标风电场中各风电机在预设时间段t内的发电量之和模型ptotal(v,n,η,t)为：

其中，r为风电机的风轮半径，ρ为风电机所处区域的空气密度，各风电机的风轮所在平面与吹入目标风电场中的自然风的风向相垂至，

基于风电机的数量n，构建各个风电机的成本之和模型cost(n)。

各个风电机的成本之和模型cost(n)为：

其中，n为目标风电场中风电机的数量。

将各个风电机的成本之和模型cost(n)和各个风电机在预设时间段t内的发电量之和模型ptotal(v,n,η,t)的比作为目标函数objective，即：

根据上式可知，目标函数和风电机的总数量、吹入目标风电场中的自然风的风速等参数相关。

步骤2：以风电场的大小和风电机安装的最小间距为约束条件，获取一组风电机数量，进而获取一组与各风电机数量相对应的预设风电机排布方案。

本方案适用于目标风电场中电机的数量n的算数平方根为整数的情况，将该算术平方根标记为n，n为整数；

将目标风电场等分为n行n列，进而获取n×n个面积相等的正方形子区域，各风电机与各正方向子区域一一对应设置，各风电机分别位于对应正方形子区域的中心点处；各风电机的风轮所在平面与吹入目标风电场中的自然风的风向相垂直

步骤3：采集吹入目标风电场中的自然风速v，根据各个风电机排布方案，基于遗传算法，应用目标函数获取与各个风电机排布方案所对应的目标函数值，将目标函数值最小的风电机排布方案作为目标风电场中风电机的最优排布方案。

图6和图7所示的风电机排布方案中，风电场为2000*2000m的正方形平坦区域，将其分别离散成10×10和20×20的小正方形区域，每台风电机位于一个小正方形区域的中心；

图8和图9所示的为两种风况，图8所示的情况中，风速恒为12m/s，风向为0°的单向风；图9所示的情况中，风速恒为12m/s，风速从0°开始以10°为步长变化，共变化36次。

当风向变化时，吹入目标风电场中的自然风的风向也会变化，以该风向为x轴的空间坐标系随风向的改变而变化，在风向变化时，参照图4图5，根据如下方法获取各排布方案中各风电机的坐标，

任选参考点建立直角坐标系x0oy0，根据风电机组相对位置确定每台风电机坐标，假设风电场内第二台风电机wt2坐标为(x2,y2)。

以正北方向为参考方向，当风向为α时，计算出迎风第一台风电机的坐标，假设是风电机wt1，其在直角坐标系x0oy0中坐标为(x1,y1)。

坐标平移，形成以风电机wt1为坐标原点的新坐标系xoy，并利用如下公式确定风电机wt2的坐标(xα2,yα2)。

以o点为圆心，把坐标系xoy逆时针旋转成坐标系x'oy'，使其横轴沿着风向，利用公式(16)确定坐标系x'oy'下其他风电机的坐标(x'α2,y'α2)。

参照上述方法，获取风向变换后各风电机在对应空间坐标系中的坐标，根据前述的输入风速计算方法计算各风电机的输入风速，进而结合构建的模型和目标函数获取最优风场布局方法。

本发明提供的考虑尾流效应的基于遗传算法的风电场布局优化方法，通过模型对比，并根据实验实测数据进一步对比，选取本发明的尾流模型，使风电场布局优化结果进一步得到优化。

以上所述仅是本发明的优选实施方式，对于本技术领域的普通技术人员来说，在不脱离本发明技术原理的前提下，还可以做出若干改进和变形，这些改进和变形也应视为本发明的保护范围。