一种基于任务感知的移动边缘计算多用户计算卸载方法

本发明属于边缘计算技术领域，具体涉及一种基于任务感知的移动边缘计算多用户计算卸载方法。

背景技术：

移动边缘计算(mobileedgecomputing，mec)在移动网络的边缘提供计算、存储和网络资源，通过将计算任务卸载到距离用户更近的边缘服务器上处理，能够有效地降低计算任务的处理时延和能耗。由于mec服务器资源有限，需要制定合理的计算卸载决策和资源分配方案，以充分利用mec中有限的资源降低用户时延与能耗，满足多用户需求。现有的任务卸载方法没有考虑任务内容对计算卸载的影响，多个相似任务的卸载可能会造成任务的重复传输和计算，浪费mec有限的资源。

对于识别辅助(如图像识别、语音识别)、虚拟现实、增强现实等一类计算任务来说，多个任务可能会调用相同的服务程序，并且当输入数据足够相似时，任务的结果大概率相同，这会造成任务程序代码重复传输和任务重复计算。

所以，需要一个新的技术方案来解决这个问题。

技术实现要素：

发明目的：为了克服现有技术中存在的移动边缘计算系统中任务卸载方法没有考虑任务内容对计算卸载的影响，造成多个任务调用相同程序或处理相似数据会造成任务重复传输和计算，浪费mec中有限计算和通信资源的问题，提供一种基于任务感知的移动边缘计算多用户计算卸载方法，可以有效减少重复数据传输以及任务重复计算。

技术方案：为实现上述目的，本发明提供一种基于任务感知的移动边缘计算多用户计算卸载方法，包括如下步骤：

s1：任务分类

根据服务器收集到系统中所有用户设备任务的相关信息，对任务进行分类；

s2：任务选择

将任务参数选择问题建模为最小支配集问题，通过基于粒子群优化的任务参数选择算法来选择出实际计算的任务和重用计算结果的任务；

s3：融合任务

将步骤s2中的实际计算的任务和重用计算结果的任务融合成新任务；

s4：利用建立好的任务卸载相关模型，根据步骤s3融合成的新任务，获取到卸载决策，各用户设备执行各自的卸载决策，进行计算卸载。

进一步地，所述步骤s1中任务分类的具体方法为：

a1：抽取程序代码摘要

获取任务程序代码的摘要，各任务的程序代码摘要可表示为

c＝(c1，c2，...，ci，...，cn)；

a2：提取输入参数的特征向量

提取任务输入参数的特征向量，各任务的输入参数特征可表示为

p＝(p1，p2，...，pi，...，pn)；

a3：上传任务信息

每个任务可表示为

其中，为任务程序代码的数据量，为任务输入参数的数据量，ui为任务的计算量，为任务所在设备的计算能力，n为任务数；

获取到任务的上述信息后，将其发送给服务器；

a4：对任务进行分类

在服务器端，根据服务器收集到的各任务程序代码摘要，进行分类，将程序代码摘要相同的任务划分为同一类，同一类的任务是使用相同的程序代码的，任务所属的类别记作gi。

进一步地，所述步骤s2中任务选择的具体方法为：

b1：任务参数特征的相似度对比

使用欧氏距离来度量各特征向量间的相似度，两个任务输入参数的欧氏距离表示为

在得到特征之间的距离后，再根据相似度大小进一步判断任务是否足够相似可重用计算结果；

假设当任务输入参数的特征距离不大于给定阈值时，任务是相似的，可进行计算结果的重用，反之，则是不相似，不可进行计算结果重用；

b2：任务参数选择问题建模

将任务参数选择建模为如下的0-1整数规划问题，约束条件为关键参数集的定义，即任意参数以及与其相邻参数中至少有一个是关键参数，优化目标是最小化关键参数集的参数个数，表示如下：

其中，x＝(x1，x2，...，xi，...，xn)表示图中每个参数是否是关键参数，若i是关键参数，则xi为1，否则，xi为0，表示所有任务的集合，n(i)表示与参数i相似的所有参数，即psg中与i相邻的所有点；

b3：基于离散二进制粒子群优化的任务参数选择策略

采用基于离散二进制粒子群优化的任务参数选择方法分别对psg中的每一个连通分支进行任务参数选择，最后得到的所有连通分支的关键参数集合之和就是整个psg的关键参数集，即得到这一类中选择进行实际计算的任务，所有psg的关键参数集合为所有任务中选中的任务参数，根据剩余的任务和选择出的实际计算的任务的相似度，确定重用计算结果的任务。

进一步地，所述步骤b3中整个psg的关键参数集的获取过程为：

c1：对于每一个连通分支，首先寻找度为0和度为1的点，如果只存在一个度为0的点，则该点构成的集合即为当前连通分支的关键参数集；如果存在度为1的点，则该点加入到关键参数集中，因为度为1的点只有1个邻点，该邻点必定属于连通分支中的某一个最小关键参数集；

c2：对于剩余的点，首先初始化粒子的数量，假设有i个粒子，粒子i的位置向量表示为

xi＝(xi1，xi2，...，xin)，i＝1，2，...，i

其中，n为参数个数，粒子位置向量作为搜索到的解，即每个参数是否是关键参数；

hi＝(hi1，hi2，...，hin)，i＝1，2，...，i

当前每个粒子最优位置表示为

当前所有粒子的最优位置中的最优值，称为当前全局最优位置，表示为

适应度函数为步骤b2所述的优化目标函数；

随后，进行不断地迭代，更新所有粒子的速度和位置；每个粒子的速度更新公式为

其中，k，k+1表示第k次，k+1次迭代，ω为惯性权重，c1与c2是学习因子，r1与r2是[0，1]之间的随机数；为更新位置，先将速度值映射为[0，1]之间的数s

粒子新位置为

每次更新位置时，要检查新位置向量是否满足步骤b2所述的约束条件，如果不满足约束条件，则不进行这一步的更新；

更新完所有粒子位置后，计算相应的适应度，根据适应度大小，更新所有粒子的局部最优值pbi和全局最优值gb。

最终，全局最优位置即为找到的解，其中值为1的参数为选中的关键参数；

求出所有的连通分支的关键参数后，合并到一起即为整个psg的关键参数。

进一步地，所述步骤s3中融合生成的新任务可表示为

其中，gi表示任务所属的类别，这由任务程序代码决定，表示任务的程序代码的数据量，表示任务的输入参数的数据量，r(i)表示重用任务计算结果的其他任务，ui表示任务所需的计算量，fi表示任务所在设备的计算能力。

进一步地，所述步骤s4中任务卸载相关模型的构建方法为：

d1：构建系统模型

假设用户设备可以通过nc个可选信道连接到mec服务器，多个信道表示为

所有任务的计算卸载决策表示为

a＝{a1，a2，...，ai，...，an′}，ai∈{0，1，...，i^c，...，n^c}

其中，ai＝0表示任务在本地进行计算，ai＝i^c表示任务由信道i^c卸载数据到mec服务器上进行实际计算；

任务传输哪些数据，可表示如下

b＝{b1，b2，...，bi，...，bn′}，bi∈{1，2}

其中，bi＝1表示用户设备只上传输入参数数据，不上传程序代码数据，bi＝2表示用户设备上传输入参数数据和程序代码数据；

d2：构建本地计算模型

新任务的本地计算时延定义为

同样地，设备产生的能耗为

其中，ζi为用户设备i单个cpu周期所产生的能耗；

d3：构建通信模型

若计算任务i进行计算卸载，其上行数据传输速率为

其中，w表示系统的无线信道带宽，pi表示用户设备i的传输功率，gi表示接入信道增益，表示高斯白噪声，此处的i′表示与用户设备i接入同一信道的其他设备；

任务i的传输时延根据是否传输代码数据可分为两种情况，表示为

任务i进行计算卸载时的传输能耗为

其中，表示用户设备i的传输功率；

d4：构建边缘计算模型

若计算任务i进行计算卸载，其在边缘服务器上的计算时延为

其中，f^o为mec服务器的计算能力；

d5：构建优化目标

用户任务的时延为

对于在本地计算的任务(ai＝0)来说，计算时延等于本地计算的时延；对于进行计算卸载的计算任务(ai＞0)来说，整个卸载过程分为三步：上传任务相关数据；在边缘服务器上执行任务；返回计算结果。

用户任务产生的能耗为

如果任务在本地计算(ai＝0)，任务的能耗等于本地计算的能耗，如果任务进行计算卸载(ai＞0)，任务的能耗只包括卸载时的数据传输能耗；

优化目标为最大化加权和o(a，b)，表示为

其中，w1，w2为权重系数。

进一步地，所述步骤s4中卸载决策的获取方法为：

建立mdp模型

mdp模型中的状态定义为每一个任务的卸载决策，时间步t时的状态表示为

st＝(a1，a2，...，ai，...，an′)

mdp模型中的动作定义为相邻状态的改变，即单个任务的卸载决策的改变，时间步t时的动作表示为

at＝{i，ai}

其中，i表示要改变决策的用户设备任务，ai，bi为用户任务i的新决策；

由进行任务卸载的设备(ai＞0)中选择传输速率最高的设备传输程序代码，其他任务直接重用其上传的程序代码，表示为

在得到卸载决策a以及b之后，即可求出对应的目标函数值；

mdp模型中的奖励函数设置为前一步决策对应的目标函数值减去新决策对应的目标函数值，表示为

rt(st，at)＝o(st)-o(st+1)

其中，o(st)，o(st+1)表示时间步t，t+1时状态对应的目标函数值，这是由所有任务的卸载决策共同决定的。

基于上述方案，本发明方法可归纳为如下两点：

1、在制定计算卸载决定之前，用户设备向mec服务器发送任务程序代码的md5码，任务输入数据特征向量(在用户设备本地通过特征提取技术得到)等任务信息，mec服务器收集到系统中所有用户设备任务的相关信息，根据任务的md5码判断任务是否使用相同的代码进行分类，对同一类中的任务根据输入数据特征向量，通过欧氏距离度量它们之间的相似度，判断哪些任务是足够相似，可进行计算结果的重用，然后将进行任务选择，将任务参数选择问题建模为最小支配集问题，通过基于粒子群优化的任务参数选择算法来选择哪些任务进行实际计算，哪些任务重用计算结果，然后再将任务融合为新的任务。

2、建立任务卸载相关模型，包括系统模型、本地计算模型、通信模型、边缘计算模型，优化目标。如果多个进行计算卸载的任务使用相同的程序代码，那么只需要传输一次代码数据，根据所建立的问题模型，建立mdp模型，通过基于深度强化学习的计算卸载决策算法得到任务的对应的卸载决策，将对应的卸载决策结果发回给终端设备。各用户设备执行各自的卸载决策，进行计算卸载。

本发明方案中当要处理的多个用户任务运行相同的代码时，可由其中一个任务传输代码，其他任务可重用已传输的代码，无需再上传任务程序代码。对于运行相同代码的任务来说，输入数据特征足够相似的任务之间可以重用计算结果。

有益效果：本发明与现有技术相比，充分利用任务内容信息，考虑任务自身内容对计算卸载的影响，利用识别辅助等一类任务的特点，通过任务程序代码和计算结果的重用，可以有效减少重复数据传输以及任务重复计算，充分利用有限计算和通信资源，从而降低多用户任务的时延与能耗，提高用户体验。

附图说明

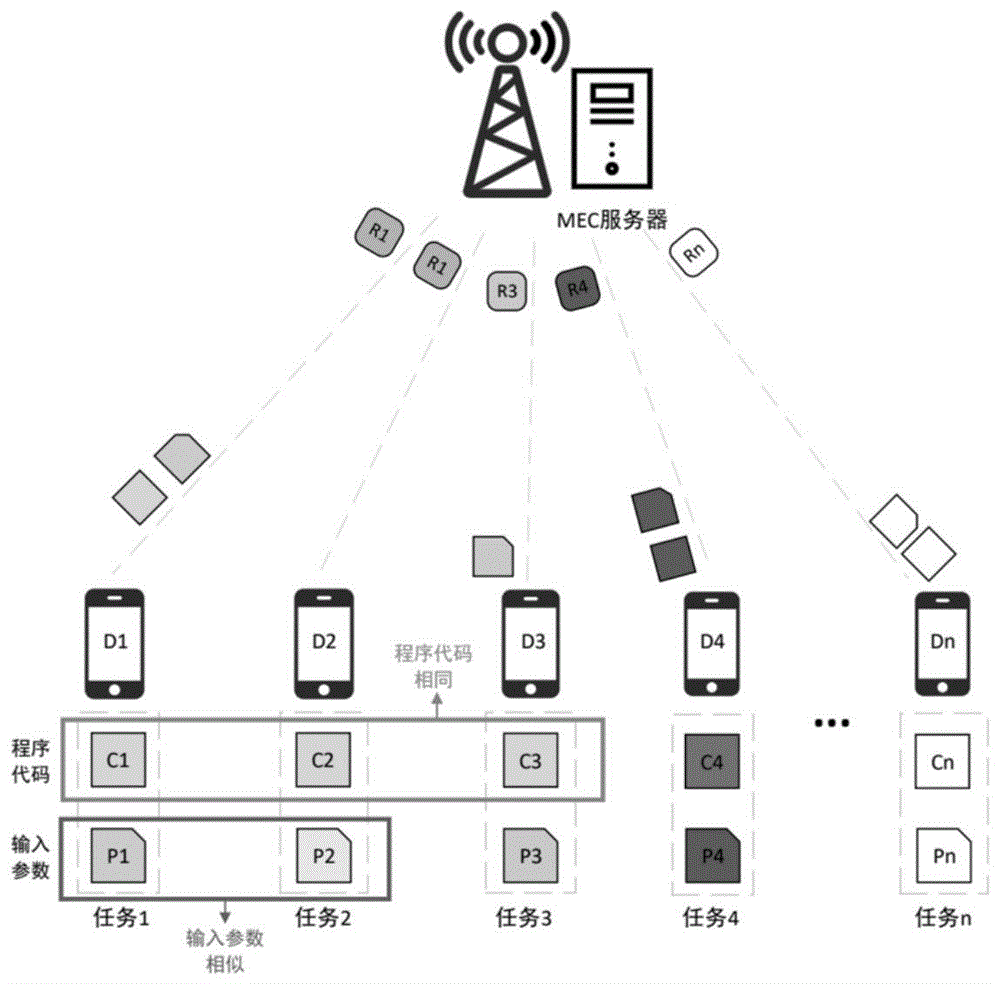
图1为本发明方法的设计思路示意图；

图2为任务融合过程示意图。

具体实施方式

下面结合附图和具体实施例，进一步阐明本发明，应理解这些实施例仅用于说明本发明而不用于限制本发明的范围，在阅读了本发明之后，本领域技术人员对本发明的各种等价形式的修改均落于本申请所附权利要求所限定的范围。

本实施例中将本发明方法应用于mec系统，本发明方法所针对的mec系统为只有一个边缘服务器计算节点，该边缘服务器可同时为多个用户设备提供服务，每一个用户设备都有一个独立且不可再分的计算任务要处理，用户设备可由多个信道向mec计算节点卸载数据。

本发明方法将任务计算所需数据分为两部分，一部分数据为任务计算所需的服务程序代码；另一部分为任务所要处理的输入参数数据。对于程序数据，在进行计算卸载时无需将所有任务的程序数据都上传，相同程序代码冗余传输会浪费mec有限的通信资源，影响多用户服务质量。因此，本实施例中提出在使用相同程序代码的多个任务中由其中一个任务上传一次程序代码，其他任务直接重用已上传的程序代码。另外，图像识别，语音识别等这类任务具有当输入数据足够相似时，输出结果会相同的特点，根据这一特点，本实施例中提出共享相似任务的计算结果以降低任务时延和能耗，一部分任务在本地或卸载到mec服务器上进行实际的计算，另一部分任务不再进行实际计算，直接重用进行实际计算的相似任务的结果。

为了更好的说明本发明方法的实现原理，参照图1进行说明，任务1，2，3的服务程序代码c1，c2，c3是相同的，只需由设备d1传输一次任务1的程序代码c1，任务2，任务3则无需再上传各自的程序代码c2和c3，直接使用已上传的程序代码c1。另外，任务1，任务2不仅程序代码相同而且输出参数p1，p2相似，任务1和任务2具有相同的计算结果，因此只需对任务1的参数1进行实际计算，即可得到任务1和任务2共同的计算结果，任务2无需进行实际计算，最终任务1的参数p1的计算结果r1既要传回给设备d1，又要发送给d2。

基于上述设计理念，以下对本发明方法进行详细说明：

本发明方法分为任务融合阶段和任务卸载决策两个阶段实现。其中步骤1～3为任务融合阶段，步骤4～5为任务卸载决策阶段。具体如下：

步骤1：任务分类

步骤1-1：抽取程序代码摘要

通过md5等信息摘要技术在设备本地获取任务程序代码的摘要，各任务的程序代码摘要可表示为

c＝(c1，c2，...，ci，...，cn)

步骤1-2：提取输入参数的特征向量

利用各种特征提取技术在用户设备本地提取任务输入参数的特征向量，各任务的输入参数特征可表示为

p＝(p1，p2，...，pi，...，pn)

对于不同类型的数据可采取特定的特征提取技术，比如对于图像数据，可采用sift在不同的尺度空间上查找图像特征点并计算特征点的方向，最终得到图像的特征向量。对于语音数据，可采用mfcc利用人耳听觉特性与频率的关系提取语音数据特征；

步骤1-3：上传任务信息

每个任务可表示为

其中，为任务程序代码的数据量，为任务输入参数的数据量，ui为任务的计算量，为任务所在设备的计算能力，n为任务数。

获取到任务的上述信息后，将其发送给mec服务器。

步骤1-4：对任务进行分类

在服务器端，根据服务器收集到的各任务程序代码摘要，进行分类，将程序代码摘要相同的任务划分为同一类，同一类的任务是使用相同的程序代码的，任务所属的类别记作gi。

步骤2：任务选择

步骤2-1：任务参数特征的相似度对比

任务分好类后，需要计算同一类内各任务间的参数特征相似度。可使用欧氏距离来度量各特征向量间的相似度，两个任务输入参数的欧氏距离表示为

在得到特征之间的距离后，再根据相似度大小进一步判断任务是否足够相似可重用计算结果。

假设当任务输入参数的特征距离不大于给定阈值时，任务是相似的，可进行计算结果的重用，反之，则是不相似，不可进行计算结果重用。数值越大表明特征间越相似，数值为0时，表示不相似。不同类型任务的相似性阈值是不同的，由任务所属的类别gi决定。

步骤2-2：任务参数选择问题建模

在得到各任务间相似关系后，需要选择哪些任务的输入参数要进行实际计算，哪些任务不用进行实际计算重用其他任务结果。

根据任务所属的类别以及任意两个任务之间的相似性，可以为每一类任务建立一个任务参数相似关系图(parametersimilaritygraph，psg)。

具体如图2所示，p1～pn表示每个任务的参数特征，在类别1对应的任务参数关系图psg1中，参数p1、p2、p3互相相似，参数p5与p3相似，p4与p2相似，p6则没有参数与之相似。类别2对应的参数相似关系图psg2中的参数p7与p8相似。参数之间的边表上的权值表示上述的参数相似度，如sim7，8表示任务参数p7、p8的相似度。

在psg图中，存在一些任务参数，能够使得图中的任意参数要么属于这些任务参数，要么与这些任务参数相似，这里将这些任务参数称为关键参数，关键参数所属的任务称为关键任务，关键参数构成的集合称为关键参数集(keyparametersset，kps)，如图2(2)psg1中的参数集{p2，p5，p6}。

如果只对关键任务进行计算，剩余非关键任务可以重用其计算结果，这样可以使全部任务都能得到计算结果。因此，为最大程度的降低任务时延和能耗，减少不必要的计算，要使得图中的关键参数数量最少，为此应从图中寻找参数数量最少的关键参数集-最小关键参数集(minimumkeyparametersset，mkps)，然后对关键任务进行实际计算。如图2(2)psg1中参数集{p1，p4，p5，p6}，{p2，p5，p6}，{p2，p3，p6}都是psg的关键参数集，而其中{p2，p5，p6}，{p2，p3，p6}的参数个数最少，为最小关键参数集。

本实施例中发现找最小关键参数集的任务参数选择问题可以转换为寻找图的最小支配集问题，这是因为根据支配集的相关定义，psg图中最小关键参数集即为图的最小支配集。最小支配集问题是np-完全问题。

将任务参数选择建模为如下的0-1整数规划问题，约束条件为关键参数集的定义，即图中任意参数以及与其相邻参数中至少有一个是关键参数，优化目标是最小化关键参数集的参数个数，表示如下：

其中，x＝(x1，x2，...，xi，...，xn)表示图中每个参数是否是关键参数，若i是关键参数，则xi为1，否则，xi为0，表示所有任务的集合，n(i)表示与参数i相似的所有参数，即psg中与i相邻的所有点。

步骤2-3：基于离散二进制粒子群优化的任务参数选择策略

为了提高搜索效率，快速求解，本实施例采用启发式算法来寻找最小关键参数集。

任务参数选择算法分别对psg图中的每一个连通分支进行任务参数选择，最后得到的所有连通分支的关键参数集合之和就是整个psg的关键参数集。

对于每一个连通分支，首先寻找度为0和度为1的点，如果只存在一个度为0的点，则该点构成的集合即为当前连通分支的关键参数集。如果存在度为1的点，则该点加入到关键参数集中，因为度为1的点只有1个邻点，该邻点必定属于连通分支中的某一个最小关键参数集。

对于剩余的点，首先初始化粒子的数量，假设有1个粒子，粒子i的位置向量表示为

xi＝(xi1，xi2，...，xin)，i＝1，2，...，i

其中，n为参数个数，粒子位置向量作为搜索到的解，即每个参数是否是关键参数。

hi＝(hi1，hi2，...，hin)，i＝1，2，...，i

当前每个粒子最优位置表示为

当前所有粒子的最优位置中的最优值，称为当前全局最优位置，表示为

适应度函数为步骤2-2所述的优化目标函数(关键参数集中参数数量)。

随后，进行不断地迭代，更新所有粒子的速度和位置。每个粒子的速度更新公式为

其中，k，k+1表示第k次，k+1次迭代，ω为惯性权重，c1与c2是学习因子，r1与r2是[0，1]之间的随机数。为更新位置，先将速度值映射为[0，1]之间的数s

粒子新位置为

每次更新位置时，要检查新位置向量是否满足步骤2-2的约束条件(关键参数集定义)，如果不满足约束条件，则不进行这一步的更新。

更新完所有粒子位置后，计算相应的适应度，根据适应度大小，更新所有粒子的局部最优值pbi和全局最优值gb。

最终，全局最优位置即为找到的解，其中值为1的参数为选中的关键参数。

求出所有的连通分支的关键参数后，合并到一起即为整个psg的关键参数，即得到这一类中选择进行实际计算的任务。所有psg的关键参数集合为所有任务中选中的任务参数。

基于离散二进制粒子群优化的任务参数选择算法的总体流程描述如下：

选择好进行计算的任务参数后，剩余任务从相似的关键任务中选取最相似的任务进行重用，如图2(2)psg1中的参数p3与p2、p5都相邻，这表示任务3即可重用参数p2的计算结果，也可以重用p5的计算结果，如果p5与p3的相似度大于p2与p3的相似度(sim3，5＞sim2，3)，则任务3重用参数p5的计算结果，而不是p2。

步骤3：融合成新任务

在选择好哪些任务的参数需要进行实际计算后，将以选中计算的任务为基础，与重用其结果的任务融合生成新任务，新任务将参与接下来的计算卸载策略的制定。

融合生成的新任务可表示为

其中，gi表示任务所属的类别，这由任务程序代码决定，表示任务的程序代码的数据量，表示任务的输入参数的数据量，r(i)表示重用任务计算结果的其他任务，ui表示任务所需的计算量(cpu周期数)，fi表示任务所在设备的计算能力。

步骤4：构建任务卸载模型

步骤4-1：构建系统模型

假设用户设备可以通过nc个可选信道连接到mec服务器，多个信道表示为

所有任务的计算卸载决策表示为

a＝{a1，a2，...，ai，...，an′}，ai∈{0，1，...，i^c，...，n^c}

其中，ai＝0表示任务在本地进行计算，ai＝i^c表示任务由信道i^c卸载数据到mec服务器上进行实际计算。

任务传输哪些数据，可表示如下

b＝{b1，b2，...，bi，...，bn′}，bi∈{1，2}

bi＝1表示用户设备只上传输入参数数据，不上传程序代码数据，bi＝2表示用户设备上传输入参数数据和程序代码数据。

步骤4-2：构建本地计算模型

计算任务的本地计算时延，应考虑重用其结果的其他任务的本地时延，因此新任务的本地计算时延定义为

同样地，设备产生的能耗为

其中，ζi为用户设备i单个cpu周期所产生的能耗。

步骤4-3：构建通信模型

若计算任务i进行计算卸载，其上行数据传输速率为

其中，w表示系统的无线信道带宽，pi表示用户设备i的传输功率，gi表示接入信道增益，表示高斯白噪声，此处的i′表示与用户设备i接入同一信道的其他设备。当多个用户设备接入相同信道时，它们之间会产生干扰，相互影响传输速率。

任务i的传输时延根据是否传输代码数据可分为两种情况，表示为

任务i进行计算卸载时的传输能耗为

其中，表示用户设备i的传输功率。

步骤4-4：构建边缘计算模型

若计算任务i进行计算卸载，其在边缘服务器上的计算时延为

其中，f^o为mec服务器的计算能力。

步骤4-5：构建优化目标

用户任务的时延为

对于在本地计算的任务(ai＝0)来说，计算时延等于本地计算的时延，对于进行计算卸载的计算任务(ai＞0)来说，整个卸载过程分为三步：上传任务相关数据；在边缘服务器上执行任务；返回计算结果。由于返回计算结果的过程中，计算结果的数据量比传输任务数据时的数据量要小得多，并且从服务器下行数据传输速率要比上行数据速率快得多，因此可以忽略返回执行结果过程是产生的时延和能耗，计算任务的时延只包括上行传输时延以及边缘服务器上处理时延

用户任务产生的能耗为

如果任务在本地计算(ai＝0)，任务的能耗等于本地计算的能耗，如果任务进行计算卸载(ai＞0)，任务的能耗只包括卸载时的数据传输能耗。

优化目标为最大化加权和o(a，b)，表示为

其中，w1，w2为权重系数。

步骤5：计算卸载算法

目标函数随着用户任务数量的增加，问题的规模会变得很大，可采用深度强化学习的方法找到最优的卸载策略，利用人工神经网络来处理大规模数据。使用强化学习方法，首先要建立马尔可夫决策过程(mdp)模型

步骤5-1：建立mdp模型

mdp模型中的状态定义为每一个任务的卸载决策，时间步t时的状态表示为

st＝(a1，a2，...，ai，...，an′)

mdp模型中的动作定义为是相邻状态的改变，即单个任务的卸载决策的改变，时间步t时的动作表示为

at＝{i，ai}

其中，i表示要改变决策的用户设备任务，ai，bi为用户任务i的新决策。

为了减少传输时延，由进行任务卸载的设备(ai＞0)中选择传输速率最高的设备(argmaxjrj(a))传输程序代码，其他任务直接重用其上传的程序代码，表示为

在得到卸载决策a以及b之后，即可求出对应的目标函数值。

mdp模型中的奖励函数设置为前一步决策对应的目标函数值减去新决策对应的目标函数值，表示为

rt(st，at)＝o(st)-o(st+1)

其中，o(st)，o(st+1)表示时间步t，t+1时状态对应的目标函数值，这是由所有任务的卸载决策共同决定的。当新的卸载决策能够获得更小的目标值时，奖励值为正值，反之为负值。

步骤5-2：基于dqn的计算卸载决策算法

因为当用户设备数量很高时，状态空间维度会很高，问题规模会很大，因此无法再使用传统的强化学习方法来解决此高维问题，因此需要引入人工神经网络，利用神经网络拟合状态值函数，可采用基于dqn的深度强化学习方法来解决该多用户计算卸载问题。

具体算法描述如下：

本实施例还提供一种基于任务感知的移动边缘计算多用户计算卸载系统，该系统包括网络接口、存储器和处理器；其中，网络接口，用于在与其他外部网元之间进行收发信息过程中，实现信号的接收和发送；存储器，用于存储能够在所述处理器上运行的计算机程序指令；处理器，用于在运行计算机程序指令时，执行上述方法的步骤。

本发明还提供一种计算机存储介质，该计算机存储介质存储有计算机程序，在处理器执行所述计算机程序时可实现以上所描述的方法。所述计算机可读介质可以被认为是有形的且非暂时性的。非暂时性有形计算机可读介质的非限制性示例包括非易失性存储器电路(例如闪存电路、可擦除可编程只读存储器电路或掩膜只读存储器电路)、易失性存储器电路(例如静态随机存取存储器电路或动态随机存取存储器电路)、磁存储介质(例如模拟或数字磁带或硬盘驱动器)和光存储介质(例如cd、dvd或蓝光光盘)等。计算机程序包括存储在至少一个非暂时性有形计算机可读介质上的处理器可执行指令。计算机程序还可以包括或依赖于存储的数据。计算机程序可以包括与专用计算机的硬件交互的基本输入/输出系统(bios)、与专用计算机的特定设备交互的设备驱动程序、一个或多个操作系统、用户应用程序、后台服务、后台应用程序等。

本领域内的技术人员应明白，本申请的实施例可提供为方法、系统、或计算机程序产品。因此，本申请可采用完全硬件实施例、完全软件实施例、或结合软件和硬件方面的实施例的形式。而且，本申请可采用在一个或多个其中包含有计算机可用程序代码的计算机可用存储介质(包括但不限于磁盘存储器、cd-rom、光学存储器等)上实施的计算机程序产品的形式。

本申请是参照根据本申请实施例的方法、设备(系统)、和计算机程序产品的流程图和/或方框图来描述的。应理解可由计算机程序指令实现流程图和/或方框图中的每一流程和/或方框、以及流程图和/或方框图中的流程和/或方框的结合。可提供这些计算机程序指令到通用计算机、专用计算机、嵌入式处理机或其他可编程数据处理设备的处理器以产生一个机器，使得通过计算机或其他可编程数据处理设备的处理器执行的指令产生用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的装置。

这些计算机程序指令也可存储在能引导计算机或其他可编程数据处理设备以特定方式工作的计算机可读存储器中，使得存储在该计算机可读存储器中的指令产生包括指令装置的制造品，该指令装置实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能。

这些计算机程序指令也可装载到计算机或其他可编程数据处理设备上，使得在计算机或其他可编程设备上执行一系列操作步骤以产生计算机实现的处理，从而在计算机或其他可编程设备上执行的指令提供用于实现在流程图一个流程或多个流程和/或方框图一个方框或多个方框中指定的功能的步骤。