一种将连续体拓扑优化结果转换为杆系结构的方法
本发明涉及结构拓扑优化技术领域,具体涉及一种将连续体拓扑优化结果转换为杆系结构的方法。
背景技术:
建筑结构优化设计技术通过调整结构构件布局可以尽可能地提高结构抵抗外力的性能,有着十分重要的应用价值。对于钢结构或钢筋混凝土框架结构而言,一般对于结构构件布局进行优化的方法多采用离散优化方法,即在确定结构的基本构件(如钢筋混凝土框架结构的梁、柱)的基础上,对于其他构件(如斜支撑等)进行布局优化,所采用的策略基本上是枚举不同的斜支撑构件的节点连接位置,获得多个斜支撑布局方案,并对每种布局方案下的结构整体进行力学行为分析,然后比较各个方案的优劣性(通常以结构的整体抗侧刚度为指标),从中选出最优的方案,即可认为其是最优拓扑。
然而,由于斜支撑等构件连接节点的可选方案往往非常多,因而上述计算方法的计算量十分巨大,这就意味着离散优化对于计算机硬件要求高,计算耗时长。相对而言,连续体拓扑优化技术具有更高的计算效率,但是连续体拓扑优化的结果往往并非杆系结构,而是设计域内的某一优化后的实体结构,这对于汽车构件制造等领域是可行的,因为非规则的实体结构可以通过模具等进行快速大批量工业化制造,然而对于建筑结构,不规则的实体构件制造成本极高,且不便于安装。
在现有的基于拓扑优化和骨架提取的杆系结构设计方法中,提取的骨架节点图是比较粗糙的,且是人为连成杆系结构的,人工干预性强,没有实现全部过程的计算机自动处理,不具有普遍性。
技术实现要素:
为了克服现有技术存在的缺陷与不足,本发明提供一种将连续体拓扑优化结果转换为杆系结构的方法,提出完整的识别杆件的准则,实现了计算机自动识别杆件并生成杆系结构,使拓扑优化结果便于进行建筑结构设计。
本发明第二目的在于提供一种将连续体拓扑优化结果转换为杆系结构的方法的应用。
本发明第三目的在于提供一种将连续体拓扑优化结果转换为杆系结构的系统;
本发明第四目的在于提供一种存储介质;
本发明第五目的在于提供一种计算设备。
为了达到上述目的,本发明采用以下技术方案:
一种将连续体拓扑优化结果转换为杆系结构的方法,包括下述步骤:
采用simp密度插值模型进行拓扑优化,得到拓扑优化结果;
将拓扑优化结果进行图形二值化处理,得到拓扑二值图;
提取拓扑骨架:对拓扑二值图进行边界扩充,构建e-8邻域检测模型,利用骨架提取算法检测拓扑二值图上当前单元e的8邻域的单元值情况,进行非骨架单元识别,舍弃非骨架单元并保留骨架单元,提取得到拓扑骨架图;
设置第一约束准则,所述第一约束准则设定为:边界约束单元和荷载作用线单元在拓扑骨架提取过程中保持为实体单元;
构建骨架节点判断模型,根据骨架节点判断模型对拓扑骨架图的骨架节点单元提取得到骨架节点图;
设置合并准则合并相近骨架节点,所述合并准则设定为:两两骨架节点计算距离,设置控制距离值,判定两骨架节点的距离小于所述控制距离值时,取两个骨架节点所连直线的几何中点为新的骨架节点,原有的两个骨架节点删除;
设置第二约束准则,所述第二约束准则设定为:当两骨架节点的距离小于控制距离值时,且该两骨架节点的其中一个是边界约束点单元或荷载作用点单元,则合并骨架节点的时另一骨架节点归并到边界约束点单元或荷载作用点单元;
任意两个骨架节点之间采用线性插值生成杆件,基于e-8邻域检测模型检测所述杆件路径上的8邻域的单元值情况,识别杆件,判定杆件路径上的8邻域实体单元的总数大于空洞单元的总数时保留杆件,否则舍弃,将保留的杆件生成杆系结构。
作为优选的技术方案,所述将拓扑优化结果进行图形二值化处理,具体步骤包括:
所述拓扑优化结果包括实体单元、空洞单元和中间单元,所述图形二值化处理将中间单元向实体单元或空洞单元转化,遍历所有单元,判定当前单元e的单元值小于预设的二值化处理阈值时,则将当前单元e置为空洞单元,否则置为实体单元,最终得到拓扑二值图。
作为优选的技术方案,所述对拓扑二值图进行边界扩充,具体步骤包括:将拓扑二值图上、下、左、右各扩充一排空洞单元。
作为优选的技术方案,所述检测拓扑二值图上当前单元e的8邻域的单元值情况,进行非骨架单元识别,判断条件包括:
检测拓扑二值图上当前单元e的8邻域是否满足实体单元个数设定阈值范围;
检测拓扑二值图上当前单元e的8邻域是否满足实体单元连续;
检测当前单元e上侧的单元是否满足8邻域内的实体单元不连续;
检测当前单元e左侧的单元是否满足8邻域内的实体单元不连续;
当判断条件均满足时,判定为非骨架单元,循环迭代判断过程直至将所有非骨架单元舍弃。
作为优选的技术方案,所述构建骨架节点判断模型,具体步骤包括:
构建多个骨架节点单元的基本判断模型,根据物体的形状旋转不变性原则,将骨架节点单元的基本判断模型旋转90°,180°,270°的得到新增判断模型,将骨架节点单元的基本判断模型与新增判断模型作为骨架节点判断模型。
作为优选的技术方案,设置控制距离值,具体步骤包括:
计算从骨架节点中任意选择两个骨架节点连成杆件的排列组合数,将两两骨架节点的距离信息储存在上三角矩阵中,上三角矩阵每行取中位数并求和再除以节点数,得到控制距离值。
为实现本发明的第二目的,本发明提供一种将连续体拓扑优化结果转换为杆系结构的方法的应用,将上述将连续体拓扑优化结果转换为杆系结构的方法应用在悬臂梁结构或简支梁结构中。
为实现本发明的第三目的,本发明提供一种将连续体拓扑优化结果转换为杆系结构的系统,包括:拓扑优化模块、二值化模块、拓扑骨架提取模块、第一约束准则设定模块、骨架节点判断模型构建模块、骨架节点提取模块、相近骨架节点合并模块、第二约束准则设定模块和杆件识别并生成模块;
所述拓扑优化模块用于采用simp密度插值模型进行拓扑优化,得到拓扑优化结果;
所述二值化模块用于将拓扑优化结果进行图形二值化处理,得到拓扑二值图;
所述拓扑骨架提取模块用于提取拓扑骨架,对拓扑二值图进行边界扩充,构建e-8邻域检测模型,检测拓扑二值图上当前单元e的8邻域的单元值情况,进行非骨架单元识别,舍弃非骨架单元并保留骨架单元,提取得到拓扑骨架图;
所述第一约束准则设定模块用于设置第一约束准则,所述第一约束准则设定为:边界约束单元和荷载作用线单元在拓扑骨架提取过程中保持为实体单元;
所述骨架节点判断模型构建模块用于构建骨架节点判断模型;
所述骨架节点提取模块用于根据骨架节点判断模型对拓扑骨架图的骨架节点单元提取得到骨架节点图;
所述相近骨架节点合并模块用于设置合并准则合并相近骨架节点,所述合并准则设定为:两两骨架节点计算距离,设置控制距离值,判定两骨架节点的距离小于所述控制距离值时,取两个骨架节点所连直线的几何中点为新的骨架节点,原有的两个骨架节点删除;
所述第二约束准则设定模块用于设置第二约束准则,所述第二约束准则设定为:当两骨架节点的距离小于控制距离值时,且该两骨架节点的其中一个是边界约束点单元或荷载作用点单元,则合并骨架节点的时另一骨架节点归并到边界约束点单元或荷载作用点单元;
所述杆件识别并生成模块用于任意两个骨架节点之间采用线性插值生成杆件,基于e-8邻域检测模型检测所述杆件路径上的8邻域的单元值情况,识别杆件,判定杆件路径上的8邻域实体单元的总数大于空洞单元的总数时保留杆件,否则舍弃,将保留的杆件生成杆系结构。
为实现本发明的第四目的,本发明提供一种存储介质,存储有程序,所述程序被处理器执行时,实现上述将连续体拓扑优化结果转换为杆系结构的方法。
为实现本发明的第五目的,本发明提供一种计算设备,包括处理器以及用于存储处理器可执行程序的存储器,所述处理器执行存储器存储的程序时,实现上述将连续体拓扑优化结果转换为杆系结构的方法。
本发明与现有技术相比,具有如下优点和有益效果:
(1)本发明采用simp密度插值原理进行拓扑优化,并在拓扑骨架提取过程中附加了约束准则,以保证边界约束和荷载作用点的存在;充分合并相近节点,消除短杆,使结果更加便于工程实际施工设计;提出完整的识别杆件的准则,实现了计算机自动识别杆件并生成杆系结构,使拓扑优化结果便于进行建筑结构设计。
(2)本发明采用边界扩充方法进行拓扑骨架提取和骨架节点提取,解决了边界约束单元和荷载作用线单元不存在8邻域的问题,使整个过程更加简洁且具有通用性。
附图说明
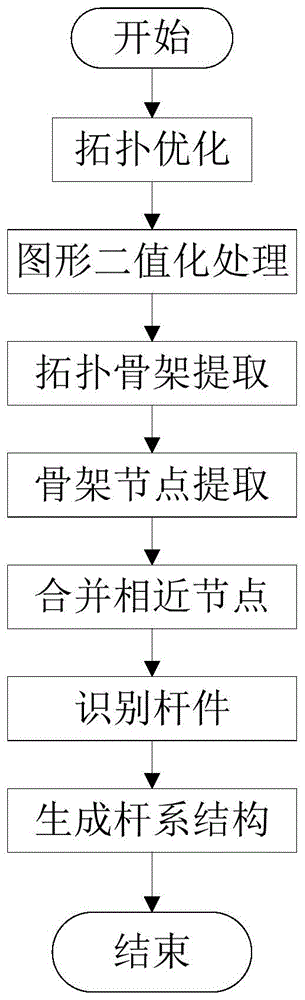
图1为本实施例1的将连续体拓扑优化结果转换为杆系结构的方法的流程示意图;
图2为本实施例1的e-8邻域检测模型示意图;
图3(a)为本实施例1的e-8邻域实体单元的连续模型第一种情况枚举示意图;
图3(b)为本实施例1的e-8邻域实体单元连续模型第二种情况枚举示意图;
图3(c)为本实施例1的e-8邻域实体单元的不连续模型第一种情况枚举示意图;
图3(d)为本实施例1的e-8邻域实体单元的不连续模型第二种情况枚举示意图;
图3(e)为本实施例1利用e-8邻域检测模型检测并提取拓扑骨架过程的示意图;
图4为本实施例1的悬空拓扑骨架图的示意图;
图5为本实施例1的边界约束单元和荷载作用线单元的示意图;
图6(a)为本实施例1的骨架节点单元四种基本判断模型示意图;
图6(b)为本实施例1的骨架节点单元13种判断模型示意图;
图7为本实施例1的杆件上三角矩阵构造示意图;
图8为本实施例1的一节点归并到边界约束点单元或荷载作用线点单元的示意图;
图9为本实施例1的杆件识别的示意图;
图10为本实施例1的二维悬臂梁的设计区域及边界条件示意图;
图11为本实施例1的拓扑优化结果示意图;
图12为本实施例1的图形二值化处理结果示意图;
图13为本实施例1的拓扑骨架提取示意图;
图14为本实施例1的骨架节点提取结果示意图;
图15为本实施例1的合并相近节点结果示意图;
图16为本实施例1的杆件识别并生成杆系结构结果示意图;
图17为本实施例1的杆件误杀和错误保留的情况对比结果示意图;
图18为本实施例2的二维简支梁的设计区域及边界条件示意图;
图19为本实施例2的半结构拓扑优化结果示意图;
图20为本实施例2的图形二值化处理结果示意图;
图21为本实施例2的拓扑骨架提取结果示意图;
图22为本实施例2的骨架节点提取结果示意图;
图23为本实施例2合并相近节点结果示意图;
图24为本实施例2杆件识别并生成杆系结构结果示意图;
图25为本实施例2简支梁拓扑结果图转化为杆系结构结果示意图。
其中,1-第一节点,2-第二节点,3-第三节点,4-第四节点,5-第五节点,6-第六节点,7-第七节点,8-第八节点,9-第九节点,10-第一杆件,11-第二杆件,13-第四杆件,14-第五杆件,15-第六杆件,16-第七杆件,17-第八杆件,18-第九杆件。
具体实施方式
为了使本发明的目的、技术方案及优点更加清楚明白,以下结合附图及实施例,对本发明进行进一步详细说明。应当理解,此处所描述的具体实施例仅仅用以解释本发明,并不用于限定本发明。
实施例1
如图1所示,本实施例提供一种将连续体拓扑优化结果转换为杆系结构的方法,具体包括下述步骤:
s1:拓扑优化
利用simp密度插值模型进行拓扑优化,得到的结果有实体单元,空洞单元和中间单元(也称灰度单元,一般位于实体单元和空洞单元的交界处),其中实体单元其值为1(黑色),空洞单元其值为0(白色),中间单元其值介于0到1之间(灰色)。
s2:图形二值化处理
二值化处理,将单元的值向0和1转化,最后变成一个拓扑二值图,因只有黑白两种颜色,又称黑白二值图。拓扑优化结果图向拓扑二值图转化,需选定一个合理的阈值,进行二值化处理,便可以将中间单元(灰色)向实体单元(黑色)和空洞单元(白色)转化。二值化处理的具体操作:遍历所有单元,判断当前单元e的单元值是否小于选定的二值化处理阈值,如果小于选定的二值化处理阈值,则当前单元e的单元值向0转化,即置为空洞单元(白色)。反之,则向1转化,即置为实体单元(黑色),最终得到拓扑二值图。
s3:提取拓扑骨架
经过二值化处理后的图形是黑白二值图,需要进一步进行拓扑骨架提取。拓扑骨架提取通过以下的拓扑骨架识别算法,保留骨架单元和消灭非骨架单元,最后得到拓扑骨架图,具体过程如下:
s31:构建e-8邻域检测模型
如图2所示,为e-8邻域的相对位置排序,其中e为当前单元,编号1~8的单元为与单元e相邻的8个单元,采用第一单元至第八单元进行说明。要判断当前单元e是否为骨架单元,需要先检测该单元的8个相邻单元,并获取其对应的单元值(空洞单元值为0,实体单元值为1)。由于边界约束单元(即边界处与各种固定端和支撑相接触的单元)和荷载作用线单元(即荷载作用线位置经过的单元)不存在8邻域的问题。本实施例采用边界扩充方法进行拓扑骨架提取和骨架节点提取。边界扩充方法,即将拓扑二值图上、下、左、右各扩充一排空洞单元(白色),如若拓扑二值图矩阵大小为m×n,则扩充后的矩阵大小为(m+2)×(n+2)。
获取了当前单元e的8邻域的单元值情况,进行判断如下:
(1)检测拓扑二值图上当前单元e的8邻域是否满足实体单元(黑色)个数为2到6个;
(2)检测拓扑二值图上当前单元e的8邻域是否满足实体单元(黑色)都连续,连续准则:如果当前单元e的8邻域中所有实体单元(黑色)相邻且不间断,即为实体单元连续。反之,如果实体单元之间存在空洞单元(白色),则实体单元不连续;
本实施例各枚举两种实体单元连续和不连续的情况,如图3(a)-图3(d)所示,图3(a)、图3(b)为实体单元连续,图3(c)、图3(d)为实体单元不连续。图3(a)中e的8邻域中第一单元、第二单元和第三单元为实体单元且相邻不间断,则为实体单元连续。同理,图3(b)中e的8邻域中第二单元、第三单元、第五单元和第八单元为实体单元且相邻不间断,则实体单元连续。图3(c)中e的8邻域中第一单元和第三单元为实体单元但不相邻,被第二单元(空洞单元)隔断,则其为实体单元不连续。同理,图3(d)中e的8邻域中第二单元、第五单元、第八单元为实体单元,第五单元和第八单元虽然相邻,但第二单元和第五单元却被第三单元(空洞单元)隔断,所以不是所有实体单元都连续,则实体单元不连续。
(3)检测拓扑二值图上当前单元e的8邻域是否满足“上,左,右”(即第二单元、第四单元、第五单元)不全为实体单元,或当前单元e上侧的单元(即第二单元)不满足8邻域内的实体单元连续;
(4)检测拓扑二值图上当前单元e的8邻域是否满足“上,左,下”(即第二单元、第四单元、第七单元)不全为实体单元,或当前单元左侧的单元(即第四单元)不满足8邻域内的实体单元连续。
如图3(e)所示,本实施例以悬臂梁为例,介绍利用e-8邻域检测模型检测并提取拓扑骨架过程。此时已不再是黑白二值图,而是黑白灰三值图,分别是2,0,1三种值。e-8邻域检测模型搜索框(即图中黑色搜索框)中心的黑色单元即为当前单元e,其值为2。e-8邻域检测模型搜索框里的灰色单元为当前单元e的8邻域中的实体单元,其值为1。e-8邻域检测模型搜索框里的白色单元为当前单元e的8邻域中的空洞单元,其值为0。e-8邻域检测模型搜索框从左至右,对拓扑二值图的所有实体单元(黑色)逐行进行检测,遍历所有实体单元(黑色)。如果当前单元e的8邻域的单元值情况同时满足以上(1)~(4)四个条件,则当前单元e为非骨架单元,其单元值设为0,变为空洞单元(白色)。然后进行下一个单元的判断,对拓扑二值图所有实体单元遍历判断结束后,更新拓扑二值图,继续重复(1)~(4)的过程进行新一轮的非骨架单元的判断。如此循环迭代,直至把所有非骨架单元消灭,最终剩下就只有骨架单元,则循环终止。
s32:经过e-8邻域检测模型的拓扑骨架提取算法的筛选,得到的拓扑骨架图可能是悬空的,即剩下的骨架单元可能与边界处的支撑失去接触,且荷载作用点处的单元也可能由于是非骨架单元而被删除,如图4所示。这与实际结构必须与边界支撑相接触以及荷载必须作用在结构上的事实情况是不相符的。所以需要附加第一约束准则进行控制,确保边界支撑处以及荷载作用点处必须存在骨架单元。第一约束准则内容是:不管怎么循环迭代,边界约束单元和荷载作用线单元在拓扑骨架提取算法的筛选过程中始终不被消灭,即边界约束单元和荷载作用线单元始终为实体单元,其值始终为1。如图5所示,图中左边一侧的两个方框标记的即为边界约束单元,图中右边一侧方框标记的即为荷载作用线单元。
s4:提取骨架节点
利用e-8邻域检测模型对拓扑骨架图的骨架单元逐个检测,对符合骨架节点要求的骨架单元保留,反之消灭,此过程用于从前述步骤得到的骨架单元中提取结构节点,具体过程如下:如图6(a)所示,图中给出的判断当前单元e是否为节点单元的基本型,其中标识为1(即单元值为1)的单元为实体单元,标识为x的单元既可以是实体单元也可以是空洞单元(即单元值为0或1)。凡是满足图6(a)所示的四种基本型的当前单元e判定为骨架节点。
由物体的形状旋转不变性可知,将图6(a)中的4种基本型旋转90°,180°,270°的所得到的判断模型也符合骨架节点的判断要求。对4种基本判断模型进行旋转并整理,一共有13种模型。其中第一种基本判断模型是中心对称的,故旋转90°,180°,270°后仍保持不变,实为一种模型。其他三种基本判断模型分别旋转90°,180°,270°又各自分别新增3种模型,合计新增9种模型,与4种基本型相加共计13种判断模型,如图6(b)所示。比较当前单元e的8邻域的0、1值情况与这13种模型的任意一种是否匹配,如果匹配,即认为当前单元e是骨架节点。
s5:合并相近节点
经过骨架节点提取步骤得到骨架节点图,如果据此节点以形成相应的杆系结构,部分节点距离过近则会出现短杆等情况,实际工程结构应尽可能避免短杆的出现,因为短杆会导致施工不便且增加接头连接数量导致成本大幅增加,与工程实际要求相背离。
但合并相近节点的过程中亦会遇到如下问题:
问题1:相近节点是个相对的概念,且准则也不尽相同,如果准则设置的距离太近,会遗漏一些相近节点,导致本应合并的节点没有合并完全。反之,如果准则设置的距离太远,又会错杀一些节点,把本不该合并的节点合并。
问题2:在合并的过程中如果不加约束,在形成杆件的过程中亦会出现悬空结构(即结构与边界支撑失去接触),且荷载也无处作用的情况(即荷载作用点处的结构合并后不再存在),这显然不符合实际结构的要求。所以应设定相应的约束准则,保证边界约束点单元和荷载作用点单元(由于此处已经经过了骨架节点的提取,故边界约束单元变为边界约束点单元,荷载作用线单元变为荷载作用点单元)的存在。
针对问题1,本发明提出合并准则的如下:两两骨架节点计算距离,设通过前述步骤已获得n个骨架节点,一共有
针对问题2的解决办法是,设置相应的第二约束准则,以保证边界约束骨架单元和荷载作用点单元的存在。第二约束准则的内容:当两节点的距离小于控制距离时,且该两节点的其中一个是边界约束点单元或荷载作用点单元,则合并节点的时候另一节点归并到边界约束点单元或荷载作用点单元。
如图8所示,提取得到多个骨架节点,包括第一节点1、第二节点2、第三节点3、第四节点4、第五节点5、第六节点6、第七节点7、第八节点8和第九节点9,其中,第三节点3归并到第一节点1,第四节点4归并到第二节点2。
s6:识别杆件
识别杆件的过程中至少存在以下问题:
问题1:杆件存在与否的问题,不是任意两个节点之间都存在杆件。方法不当则会误杀杆件,或者产生了原本不该存在的杆件。
问题2:两个节点之间先用线性插值生成杆件,这种方法生成的杆件与拓扑骨架图的杆件位置会有所偏差,原因是前面拓扑骨架提取这一步和上一步合并相近节点导致的,这就加剧了杆件识别的难度。
解决以上两个问题的具体做法是:
以悬臂梁结构为例,介绍杆件识别具体过程,如图9所示,第一节点1和第三节点3之间先用线性插值生成杆件,此时已不再是黑白二值图,而是黑白浅灰深灰四值图,分别是1,-2,-1,0四种值。在杆件路径上,黑色单元是实体单元,其值为1。浅灰色单元为生成的杆件单元与拓扑骨架单元相重合的单元,故亦是实体单元,其值为-1。而白色单元则是空洞单元,其值为-2。深灰色单元为背景单元,其值为0。利用e-8邻域检测模型检测该杆件路径上的8邻域的单元值情况,如果该杆件路径上的8邻域实体单元的总数大于空洞单元的总数,则认为此处有杆件;反之,此处则不存在杆件。如此便可以有效的解决杆件存在与否的问题以及杆件位置偏差问题。该不存在的杆件消灭,该存在的杆件保留,最后便可以生成杆系结构,整个拓扑骨架提取的全过程到此就结束了。
本实施例以悬臂梁结构为例,具体说明将连续体拓扑优化结果转换为杆系结构的方法的实现方式。
如图10所示,结构拓扑优化的设计空间为60mm×30mm的长方形区域,在结构的左边的竖直边上约束其x,y两个方向的自由度,在其相对的右端底角出施加1kn的垂直向下的集中载荷,设计区域材料的弹性模量为1gpa,泊松比为0.3。对于二维结构,本实施例采用1mm×1mm的正方形单元对整体结构进行有限元离散化,针对本实施例,离散后的悬臂梁结构具有1800个有限元单元。
采用simp密度插值模型求解本实施例,使用matlab编程,惩罚因子p为3,过滤半径取1.5,移动极限m为0.2,阻尼因子选取为0.5,如图11所示,得到最终结构的拓扑优化结果,图形二值化处理的阈值取0.75,如图12所示,得到图形二值化处理后的结果。如图13所示,得到拓扑骨架提取结果,该拓扑骨架保持了原有的拓扑构型,边界条件也符合工程实际。
如图14所示,利用e-8邻域检测模型与13种骨架节点模型一一比对,得到骨架节点图。如图15所示,合并相近节点,得到最终骨架节点图。如图16所示,识别杆件,将不存在的杆件消灭,将存在的杆件保留,最后生成杆系结构。
针对不同结构类型,二值化处理阈值的范围是不一样的。选取的二值化处理阈值是否合理会直接影响后续的识别杆件这一操作,此实施例的二值化处理阈值如果选取为0.58,如图17所示,得到最后的杆件识别结果,原本可以得到第一杆件10、第二杆件11、第四杆件13、第五杆件14、第六杆件15、第七杆件16和第八杆件17;从图中可以发现,原本应该存在的第五杆件14和第六杆件15被误杀,原本不该存在的第九杆件18却被保留下来了。原因是拓扑骨架图的杆件位置与利用骨架节点图线性插值生成的杆件位置会有偏差,利用杆件识别准则进行杆件识别时,虽然可以减少一部分偏差,但当杆件偏差过大时,就会导致杆件被误杀的情况,即生成的第五杆件14和第六杆件15与拓扑骨架图中第五杆件14和第六杆件15位置偏差过大而被误杀。同理,当各杆件位置离得太近的时候,又会影响到周边杆件的识别,第九杆件18的出现则是因为受到拓扑骨架图中第五杆件14和第六杆件15的影响。
实施例2
本实施例以简支梁结构为例,具体说明将连续体拓扑优化结果转换为杆系结构的方法的实现方式,具体如下:
如图18所示,二维简支梁结构拓扑优化设计区域为120mm×20mm的长方形区域,在结构的左下角节点约束其两个方向的自由度,在右下角节点处约束其y方向自由度,在其中间顶部施加2kn的垂直向下的集中载荷,设计区域材料的弹性模量为1gpa,泊松比为0.3。对于二维简支梁结构,本实施例仍然采用1mm×1mm的四边形单元对整体结构进行有限元离散化,针对本实施例,离散后的悬臂梁结构具有2400个四边形结构单元。由于是对称结构,可取结构的一半进行拓扑优化。
采用simp密度插值模型求解本实施例,使用matlab编程,惩罚因子p为3,过滤半径取1.5,移动极限m为0.2,阻尼因子选取为0.5。如图19所示,得到半结构拓扑优化结果。图形二值化处理阈值取0.60,如图20所示,得到二值化处理的结果。如图21所示,得到拓扑骨架提取结果图,该拓扑骨架保持了原有的拓扑构型,边界条件也符合工程实际。
利用e-8邻域检测模型与13种骨架节点模型一一比对,如图22所示,得到骨架节点图。合并相近节点,如图23所示,得到最终骨架节点图。识别杆件,将不存在的杆件消灭,将存在的杆件保留,如图24所示,最后生成杆系结构。利用对称性,如图25所示,最终得到简支梁结构转化为杆系结构结果。
实施例3
本实施例提供一种将连续体拓扑优化结果转换为杆系结构的系统,包括:拓扑优化模块、二值化模块、拓扑骨架提取模块、第一约束准则设定模块、骨架节点判断模型构建模块、骨架节点提取模块、相近骨架节点合并模块、第二约束准则设定模块和杆件识别并生成模块;
在本实施例中,拓扑优化模块用于采用simp密度插值模型进行拓扑优化,得到拓扑优化结果;
在本实施例中,二值化模块用于将拓扑优化结果进行图形二值化处理,得到拓扑二值图;
在本实施例中,拓扑骨架提取模块用于提取拓扑骨架,对拓扑二值图进行边界扩充,构建e-8邻域检测模型,利用骨架提取算法检测拓扑二值图上当前单元e的8邻域的单元值情况,进行非骨架单元识别,舍弃非骨架单元并保留骨架单元,提取得到拓扑骨架图;
在本实施例中,第一约束准则设定模块用于设置第一约束准则,所述第一约束准则设定为:边界约束单元和荷载作用线单元在拓扑骨架提取过程中保持为实体单元;
在本实施例中,骨架节点判断模型构建模块用于构建骨架节点判断模型;
在本实施例中,骨架节点提取模块用于根据骨架节点判断模型对拓扑骨架图的骨架节点单元提取得到骨架节点图;
在本实施例中,相近骨架节点合并模块用于设置合并准则合并相近骨架节点,所述合并准则设定为:两两骨架节点计算距离,设置控制距离值,判定两骨架节点的距离小于所述控制距离值时,取两个骨架节点所连直线的几何中点为新的骨架节点,原有的两个骨架节点删除;
在本实施例中,第二约束准则设定模块用于设置第二约束准则,所述第二约束准则设定为:当两骨架节点的距离小于控制距离值时,且该两骨架节点的其中一个是边界约束点单元或荷载作用点单元,则合并骨架节点时另一骨架节点归并到边界约束点单元或荷载作用点单元;
在本实施例中,杆件识别并生成模块用于任意两个骨架节点之间采用线性插值生成杆件,基于e-8邻域检测模型检测所述杆件路径上的8邻域的单元值情况,识别杆件,判定杆件路径上的8邻域实体单元的总数大于空洞单元的总数时保留杆件,否则舍弃,将保留的杆件生成杆系结构。
实施例4
本实施例公开了一种存储介质,存储有程序,所述程序被处理器执行时,实现实施例1的将连续体拓扑优化结果转换为杆系结构的方法,本实施例中的存储介质可以是磁盘、光盘、计算机存储器、只读存储器(rom,read-onlymemory)、随机存取存储器(ram,randomaccessmemory)、u盘、移动硬盘等介质。
实施例5
本实施例公开了一种计算设备,包括处理器以及用于存储处理器可执行程序的存储器,所述处理器执行存储器存储的程序时,实现实施例1的将连续体拓扑优化结果转换为杆系结构的方法,本实施例中的计算设备可以是台式电脑、笔记本电脑、智能手机、pda手持终端、平板电脑或其他具有处理器功能的终端设备。
上述实施例为本发明较佳的实施方式,但本发明的实施方式并不受上述实施例的限制,其他的任何未背离本发明的精神实质与原理下所作的改变、修饰、替代、组合、简化,均应为等效的置换方式,都包含在本发明的保护范围之内。
- 还没有人留言评论。精彩留言会获得点赞!