一种基于RBF神经网络的农村住房台风灾害预估方法与流程

一种基于rbf神经网络的农村住房台风灾害预估方法
技术领域
1.本发明涉及灾害天气预测技术领域，具体是涉及一种基于rbf神经网络的 农村住房台风灾害预估方法。


背景技术：

2.我国是台风重灾国家，近年来随着全球气候变暖，西太平洋生成台风的平 均强度呈下降趋势，但我国台风平均登陆强度呈逐渐增强趋势。台风是海洋与 大气相互作用的产物之一，通常伴随着强风、大雨和风暴潮。其破坏力极强且 常会引发洪水、泥石流等次生灾害。根据资料统计台风是历年影响沿海城市各 种气象灾害之最，而且倒塌房屋和死亡人数的平均数为最高，相较于城市，农 村住房抗风性能较差，特别是一些老旧农房，极易遭受台风破坏。
3.根据全国第三次农业普查数据显示，农户住房主要为砖混和砖(石)木结 构。住房为砖混结构的13182万户，占57.2％；砖(石)木结构的5993万户， 占26.0％；钢筋混凝土结构的2884万户，占12.5％；竹草土坯结构的640万户， 占2.8％；其他结构的329万户，占1.4％。除了抗风性能较好的钢筋混凝土结构 外，砖混、砖石、竹草等结构房屋都可能因为台风来临而倒塌。因此，对农房 进行合理的灾情评估及预测显得愈发重要。
4.针对台风灾害问题，国内外不少学者进行了研究。在致灾因子危险性方面， 有学者基于综合灾情关联度及台风灾致灾因子建立台风灾情预估模型；有学者 以上海年最大风速作为应用对象，采用概率统计方法对致灾因子危险度进行定 量诊断；有学者建立基于主成分分析法的神经网络，并以直接经济损失指数作 为评估指标对浙江省5个台风进行拟合评估。在承灾体易损性方面，有学者综 合考虑致灾因子和承灾体特征并依据自然灾害系统理论对中国沿海地区台风灾 害危险性进行分析；有学者通过建立基于层次分析法的指标系统对中国沿海地 区台风引发的灾害风险进行评估；有学者把台风灾害与社会经济因子相结合， 指出造成灾情损失的主要原因与人口、经济通货密切相关；有学者利用浙江省 农村住房保险数据建立了浙江省农村住房台风易损性方程并给出相关参数。
5.目前国内各地应急管理部门主要通过基层灾害信息员收集汇总台风灾情数 据，数据时间序列长，人为干扰因素多，历史数据质量不理想，且侧重于统计 受灾居民数量、人员伤亡、直接经济损失等民政指标，其统计的台风灾情数据 缺乏统一标准，灾情数据的整理与修正存在困难。而气象水利等部门基于历史 数据且主要集中于致灾因子统计，选取相关因素因子，基本上都是通过台风产 生的极大风速和累积雨量这两个测量值与台风灾害的影响程度确定权重系数， 最后构建台风灾害综合风险区划模型，得到风险区划结果，但是不能精确到各 乡镇、村的风险区划，因此气象水利等部门提供的灾情数据空间分辨率较低， 缺少承灾体统计，缺乏量化评估台风灾害风险。
6.因此，对于气象或政府等业务部分而言，实现对未来台风可能造成灾害损 失的预估更具有现实意义。


技术实现要素：

7.针对现有技术中存在的上述问题，旨在提供一种基于rbf神经网络的农村 住房台风灾害预估方法，有效建立从致灾因子到承灾体损失的台风灾情评估模 型，解决传统风险评估空间分辨率较低、风险度量难的问题，精确到各乡镇、 村的风险灾害预估，量化评估台风灾害风险，为后续制定台风灾害保险政策、 台风应急预案等应用提供科学依据。
8.具体技术方案如下：
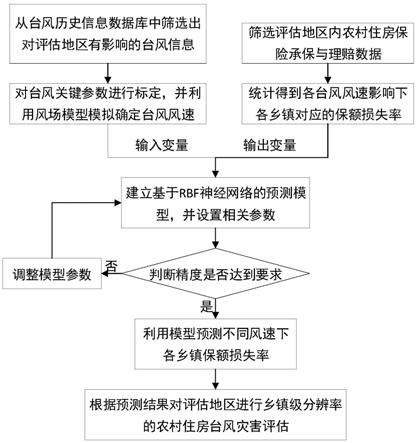
9.一种基于rbf神经网络的农村住房台风灾害预估方法，包括以下步骤：
10.步骤1：从台风历史信息数据库中筛选出对评估地区有影响的台风信息；
11.步骤2：对筛选出的台风信息进行台风关键参数标定，并利用风场模型模拟 确定台风风速；
12.步骤3：根据评估地区内农村住房保险承保与理赔数据，获取各台风灾害影 响下各乡镇农村住房对应的保额损失率；
13.步骤4：建立基于rbf神经网络的预测模型，将得到的台风风速数据作为预 测模型的输入变量、将得到的保额损失率数据作为预测模型的输出变量代入预 测模型进行训练，获取最优的rbf神经网络结构；
14.步骤5：通过预测模型预测得到不同台风风速下各乡镇保额损失率，根据预 测结果对评估地区进行乡镇级分辨率的农村住房台风灾害评估。
15.相较于现有技术，本发明利用rbf神经网络有效建立了从致灾因子到承灾 体损失的台风灾情评估模型，借助公共巨灾保险数据可以实现乡镇级高分辨率 的农村住房台风灾情预估，解决传统风险评估空间分辨率较低、风险度量难的 问题，精确到各乡镇、村的风险灾害预估，量化评估台风灾害风险，为后续制 定台风灾害保险政策、台风应急预案等应用提供科学依据，可有效减少因风致 倒塌造成的人员伤亡和经济损失。
16.进一步的，在步骤4中，rbf神经网络结构包括输入层、隐含层和输出层；
17.输入层的每个输入样本为：其中，x
p
表示台风风速，m 代表输入样本数量，t表示对输入样本组成的矩阵的转置；
18.输入层通过径向基函数实现x
p
→
r(x
p
‑
c
i
)的空间非线性映射变换，其激活 函数为：其中，r(x
p
‑
c
i
)为映射值，exp()表 示以e为底的指数函数，||x
p
‑
c
i
||为欧式距离，c
i
为隐含层节点中心，σ为基函数 方差；
19.输出层通过加权组合实现r(x
p
‑
c
i
)
→
y
j
的线性映射，表示为： j＝1,2,...,n(n为输出层个数)，其中，ω
ij
为隐含层到输 出层的连接权值,i＝1,2,3...,h(h为训练样本对应的隐含层节点数)，y
j
为数据 对应的第j个保额损失率输出值。
20.本发明提供的该rbf神经网络结构简单，收敛速度快，总体预测误差小。
21.进一步的，在步骤4中，具体包括如下步骤：
22.步骤41：随机选取i个互不相同的向量作为初始聚类中心c
i
(0)(i＝1,2,3,...h)， 并预先设定阈值ε的值，通过计算获取最终隐含层中心c
i
(h)；
23.步骤42：求解方差σ，表示为i＝1,2,...,h(h为训练样本对应的 隐含层节点数)，其中，c
max
是选取中心之间的最大距离；
24.步骤43：计算连接权值ω
ij
为：i＝1,2,...,h(h表示 训练样本对应的隐含层节点数)，其中，c
max
是选取中心之间的最大距离。
25.进一步的，获取最终隐含层中心c
i
(h)的具体计算方法包括如下步骤：
26.步骤411：计算各台风风速与聚类中心点的欧式距离，表示为：||x
p
‑
c
i
(h)||， 其中，p＝1,2,3....m，i＝1,2,3,...h；
27.步骤412：根据各台风风速x
p
与聚类中心的最小欧式距离确定其归类，即当i
*
(x
p
)＝min||x
p
‑
c
i
(h)||时，x
p
被归为第i
*
类，从而将全部样本划分为i个子集： u1(n),u2(n),...u
i
(n)；
28.步骤413：采用竞争学习规则进行调整，表示为：
[0029][0030]
步骤414：计算|c
i
(h+1)
‑
c
i
(h)|，当|c
i
(h+1)
‑
c
i
(h)|＜ε时，获取最终隐含层中 心c
i
(h)；否则令h＝h+1,并跳到步骤411。
[0031]
本发明通过不断迭代试验，获取rbf神经网络的最优权值，进而快速获取 最优的rbf神经网络。
[0032]
进一步的，在步骤1中，以台风路径经过评估地区500km范围为原则筛选 台风信息，并根据台风登陆点到评估地区的距离，分为三类：ⅰ型，登陆地为 评估地区所在省份；ⅱ型，登陆地为评估地区相邻省份；ⅲ型，登陆地为较远 地区或未登陆但台风中心路径进入评估地区500km范围内。通过此，对原始台 风信息数据进行筛选，选择对评估地区有影响的台风信息进行整理、归类、分 析，以保证输入样本变量的准确性，提高预测模型的预测精度。
[0033]
进一步的，在步骤2中，采用vickery经验模型对台风关键参数进行计算， 采用yan meng风场模型模拟得到各台风影响下评估地区近地面10m高度处的 10min平均最大风速。通过此，能准确得到台风风速数据，以保证输入样本变量 的准确性，提高预测模型的预测精度。
[0034]
进一步的，在步骤2中的台风关键参数包括最大风速半径r
max
、holland气 压剖面参数b和中心气压。
[0035]
进一步的，在步骤3中，根据出险地址可精确定位农村住房安全事故发生 的乡镇或街道以实现乡镇级分辨率灾情评估。
[0036]
进一步的，在步骤4中，根据训练曲线收敛程度以及数据误差的精度要求 来检验得到的预测模型的准确性，若满足要求，则继续进行步骤5；否则，跳到 步骤42重新设置阈值ε的值。通过此，检测预测模型的准确性，获取最优的rbf 神经网络模型。
[0037]
进一步的，在步骤5中，通过预测模型对不同设计台风风速下各乡镇保额 损失率
进行预测，根据预测结果得到台风风速影响下最大保额损失率及对应的 乡镇，并生成评估报告。
[0038]
本发明提供的该预估方法可推广到其他区域进行台风灾害风险评估分析， 有利于城市各乡镇防震减灾工作的开展，具有非常重要的现实意义。
附图说明
[0039]
图1为本发明基于rbf神经网络的农村住房台风灾害预估方法的流程图；
[0040]
图2a为本发明实施例中ⅰ型1416号台风影响下宁波市各乡镇保额损失率；
[0041]
图2b为本发明实施例中ⅰ型1509号台风影响下宁波市各乡镇保额损失率；
[0042]
图2c为本发明实施例中ⅰ型1814号台风影响下宁波市各乡镇保额损失率；
[0043]
图2d为本发明实施例中ⅰ型1909号台风影响下宁波市各乡镇保额损失率；
[0044]
图2e为本发明实施例中ⅰ型1918号台风影响下宁波市各乡镇保额损失率；
[0045]
图3a为本发明实施例中ⅱ型1410号台风影响下宁波市各乡镇保额损失率；
[0046]
图3b为本发明实施例中ⅱ型1614号台风影响下宁波市各乡镇保额损失率；
[0047]
图3c为本发明实施例中ⅱ型1709号台风影响下宁波市各乡镇保额损失率；
[0048]
图3d为本发明实施例中ⅱ型1710号台风影响下宁波市各乡镇保额损失率；
[0049]
图3e为本发明实施例中ⅱ型1808号台风影响下宁波市各乡镇保额损失率；
[0050]
图3f为本发明实施例中ⅱ型1810号台风影响下宁波市各乡镇保额损失率；
[0051]
图3g为本发明实施例中ⅱ型1812号台风影响下宁波市各乡镇保额损失率；
[0052]
图3h为本发明实施例中ⅱ型1818号台风影响下宁波市各乡镇保额损失率；
[0053]
图4a为本发明实施例中ⅲ型1407号台风影响下宁波市各乡镇保额损失率；
[0054]
图4b为本发明实施例中ⅲ型1408号台风影响下宁波市各乡镇保额损失率；
[0055]
图4c为本发明实施例中ⅲ型1412号台风影响下宁波市各乡镇保额损失率；
[0056]
图4d为本发明实施例中ⅲ型1616号台风影响下宁波市各乡镇保额损失率；
[0057]
图4e为本发明实施例中ⅲ型1618号台风影响下宁波市各乡镇保额损失率；
[0058]
图4f为本发明实施例中ⅲ型1703号台风影响下宁波市各乡镇保额损失率；
[0059]
图4g为本发明实施例中ⅲ型1718号台风影响下宁波市各乡镇保额损失率；
[0060]
图4h为本发明实施例中ⅲ型1819号台风影响下宁波市各乡镇保额损失率；
[0061]
图4i为本发明实施例中ⅲ型1825号台风影响下宁波市各乡镇保额损失率；
[0062]
图4j为本发明实施例中ⅲ型1905号台风影响下宁波市各乡镇保额损失率；
[0063]
图4k为本发明实施例中ⅲ型1913号台风影响下宁波市各乡镇保额损失率；
[0064]
图4l为本发明实施例中ⅲ型1917号台风影响下宁波市各乡镇保额损失率；
[0065]
图5为本发明实施例中2014
‑
2019年因台风导致的宁波各乡镇农房保额总 损失率；
[0066]
图6为本发明实施例中rbf神经网络结构的原理图；
[0067]
图7为rbf神经网络模型训练曲线图；
[0068]
图8为bp神经网络模型训练曲线图；
[0069]
图9为bp和rbf神经网络模型预测值与实际的保额损失率对比图；
[0070]
图10为bp与rbf模型预测结果均方误差对比图；
[0071]
图11a为rbf神经网络预测10年一遇设计风速下的损失率；
[0072]
图11b为rbf神经网络预测50年一遇设计风速下的损失率；
[0073]
图11c为rbf神经网络预测100年一遇设计风速下的损失率。
具体实施方式
[0074]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清 楚、完整地描述，显然，所描述的实施例仅仅是本发明的一部分实施例，而不 是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创 造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0075]
请参阅图1，其为本发明基于rbf神经网络的农村住房台风灾害预估方法的 流程图，该基于rbf神经网络的农村住房台风灾害预估方法包括以下步骤：
[0076]
步骤1：从台风历史信息数据库中筛选出对评估地区有影响的台风信息。
[0077]
以台风路径经过评估地区500km范围为原则，从评估地区气象站和 cma
‑
sti热带气旋最佳路径数据集中筛选出对评估地区有影响的台风信息，信 息包括：台风编号及名称、台风起始时间、台风终止时间、台风影响评估地区 时间、气象站观测到的台风风速、台风路径中心气压和台风路径经纬度。台风 路径信息根据登陆点到评估地区的距离，分为三类：ⅰ型，登陆地为评估地区 所在省份；ⅱ型，登陆地为评估地区相邻省份；ⅲ型，登陆地为较远地区或未 登陆但其中心路径进入评估地区500km范围内。
[0078]
在一个实施例中，以台风路径经过宁波区域500km范围为原则，从气象站 和cma
‑
sti热带气旋最佳路径数据集中筛选出2014
‑
2019年对宁波地区有影响 的25条台风路径信息,并根据路径信息可将台风分为三种类型：ⅰ型，登录点 为宁波、台州等浙江沿海地区；ⅱ型，登陆点为福建、上海等相邻省市；ⅲ型， 登陆点为广东等较远地区或未登陆但其中心路径进入宁波500公里范围内。
[0079]
步骤2：对筛选出的台风信息进行台风关键参数标定，并利用风场模型模拟 确定台风风速。
[0080]
在一个实施例中，由于发现在台风影响期间气象站观测得到的日最大10min 平均风速偏小，因此本文采用yan meng风场模型模拟宁波地区近地面台风风速。 在进行风场模拟之前需要对台风关键参数进行标定，采用vickery经验模型确定 最大风速半径r
max
、holland气压剖面参数b和中心气压等关键参数取值；并采 用yan meng风场模型模拟确定台风风速，模拟得到25条台风影响下宁波地区 近地面10m高度处的10min平均最大风速。
[0081]
请参阅表1，其为本发明一个实施例中筛选出的25条台风特征信息表。
[0082]
表1：25条台风特征信息
[0083][0084][0085]
由表1可知，2014
‑
2019年平均每年影响宁波地区的台风为4至5个。这其 中，登陆浙江沿海并对宁波造成严重影响的i型台风平均每年发生1次。筛选 出的25条台风平均影响宁波3至4天，短的持续影响时间只有1天(1918号“米 娜”台风)，长的持续影响时间达到8天(1812号“云雀”台风)。
[0086]
步骤3：根据评估地区内农村住房保险承保与理赔数据，获取各台风灾害影 响下各乡镇农村住房对应的保额损失率。
[0087]
根据评估地区内农村住房保险承保与理赔数据，统计得到各台风灾害影响 下各乡镇对应的保额损失率。各乡镇保额损失率等于各乡镇总实赔金额与各乡 镇总保险费的比值。
[0088]
农村住房保险数据内容包括承保与理赔数据：承保数据是从保单中提取保 单号、被保户数、承保地址、每户保险金额、总保险费等指标；理赔数据包括 保单号、出险日期、出险原因、出险地址、保险标的损失、实赔金额等。两类 数据中保单号相互对应，利用出险地址可精确定位农村住房安全事故发生的乡 镇或街道以实现乡镇级分辨率灾情评估。
[0089]
在一个实施例中，统计2014
‑
2019年不同台风路径影响下宁波各乡镇的农房 保额损失率，选取具有代表性的台风进行分析，25条台风影响下宁波市各乡镇 保额损失率具体见图2a至图4l。从图中不难看出不同登陆地的台风造成的灾损 差异较大，乡镇保额损失率总体和影响宁波地区的台风风速呈正相关关系，也 就是说，浙江沿海登陆的台风(i型台风)对宁波地区农房造成的损失比在福建 等相邻省市登陆的台风(ii型台风)要大，特别是1509号台风“灿鸿”以及1909 号台风“利奇马”对乡镇农房产生了巨大破坏。而iii型台风，如1616号台风
ꢀ“
马勒卡”，虽然未登陆且影响宁波地区的风速不大，但在演变过程中其中心 路径进入宁波500km范围内，对宁波各乡镇农房仍然造成了较大损失，其主要 原因是在该台风螺旋风雨带的袭击下，宁波山区发生了洪涝、滑坡、泥石流等 次生灾害，而农村住房极易遭受次生灾害破坏。
[0090]
对2014
‑
2019年投保数据和因台风导致的理赔数据按照区县尺度进行汇总 整理，具体信息如表2所示。
[0091]
表2宁波各区县因台风导致的农房出险数据汇总
[0092]
[0093][0094]
由表2可以看出当前宁波各区县乡镇的投保情况差异较大。慈溪由于人口 基数大，投保总金额明显高于其他区县。总赔付金额较高的区县为余姚、象山、 宁海、慈溪。保额损失率较大的区县为象山、北仑、宁海、余姚。
[0095]
为了更直观分析台风灾害保险与农村住房风险的关系，图5展示了 2014
‑
2019年因台风导致的宁波各乡镇农房保额总损失率。结合表2可以看出， 作为台风多次登录地的宁波象山，保额损失率是宁波区域中最大的，象山县内 的茅洋乡保额损失率更是接近0.01％。另外，北仑、宁海、余姚这些区域的保额 损失率均高于宁波地区平均值，其中北仑梅山乡、宁海茶院乡、余姚鹿亭乡损 失率分别为0.007252％、0.003258％、0.009502％。结合这些乡镇的具体位置可 知，由于这些乡镇均属于山区乡镇，山区房屋主要以砖(石)混结构为主，此 类结构体系很难抵御台风带来的强风暴雨影响。因此，这些区域的保额损失率 较大，房屋结构有较大的损坏风险。
[0096]
步骤4：建立基于rbf神经网络的预测模型，将得到的台风风速数据作为预 测模型的输入变量、将得到的保额损失率数据作为预测模型的输出变量代入预 测模型进行训练，获取最优的rbf神经网络结构。
[0097]
径向基函数神经网络(radial basis function neural network,以下简称 rbf神经网络)是一种三层前馈神经网络，能够逼近任意非线性函数，具有良好 的全局逼近性能和泛化能力，并且学习收敛速度快。
[0098]
请参阅图6，其为本发明实施例中rbf神经网络结构的原理图。在rbf神经 网络中，第一层为输入层，进行样本的输入，输入层节点的个数就是样本的维 度。第二层为隐含层，也称径向基层，节点的激活函数使用的是径向基函数， 隐含层对输入样本进行非线性变换，将低维空间映射到高维的空间上，解决低 维空间不可解的问题。第三层为输出层，也称为线性层，隐含层和输出层之间 有权值连接，它是将隐含层的输出进行一种线性变换。
[0099]
本发明中，每个样本都是一个向量，输入层的每个输入样本为：
[0100]
[0101]
其中，x
p
表示台风风速，m代表输入样本数量，t表示对输入样本组成的矩 阵的转置。
[0102]
输入层通过径向基函数实现x
p
→
r(x
p
‑
c
i
)的空间非线性映射变换，其激活 函数为：
[0103][0104]
其中，r(x
p
‑
c
i
)为映射值，exp()表示以e为底的指数函数，||x
p
‑
c
i
||为欧 式距离，c
i
为隐含层节点中心，σ为基函数方差。
[0105]
输出层通过加权组合实现r(x
p
‑
c
i
)
→
y
j
的线性映射，表示为：
[0106]
j＝1,2,...,n(n为输出层个数)
[0107]
其中，ω
ij
为隐含层到输出层的连接权值,i＝1,2,3...,h(h为训练样本对应的 隐含层节点数)，y
j
为数据对应的第j个保额损失率输出值。
[0108]
步骤4中，具体包括如下步骤：
[0109]
步骤41：随机选取i个互不相同的向量作为初始聚类中心c
i
(0)(i＝1,2,3,...h)， 并预先设定阈值ε的值，通过计算获取最终隐含层中心c
i
(h)。
[0110]
其中，获取最终隐含层中心c
i
(h)的具体计算方法包括如下步骤：
[0111]
步骤411：计算各台风风速与聚类中心点的欧式距离，表示为：||x
p
‑
c
i
(h)||， 其中，p＝1,2,3....m，i＝1,2,3,...h；
[0112]
步骤412：根据各台风风速x
p
与聚类中心的最小欧式距离确定其归类，即当 i*(x
p
)＝min||x
p
‑
c
i
(h)||时，x
p
被归为第i*类，从而将全部样本划分为i个子集： u1(n),u2(n),...u
i
(n)；
[0113]
步骤413：采用竞争学习规则进行调整，表示为：
[0114][0115]
步骤414：计算|c
i
(h+1)
‑
c
i
(h)|，当|c
i
(h+1)
‑
c
i
(h)|＜ε时，获取最终隐含层中 心c
i
(h)；否则令h＝h+1,并跳到步骤411。
[0116]
步骤42：求解方差σ，表示为i＝1,2,...,h(h为训练样本对应的 隐含层节点数)，其中，c
max
是选取中心之间的最大距离。
[0117]
步骤43：计算连接权值ω
ij
为：i＝1,2,...,h(h表示 训练样本对应的隐含层节点数)，其中，c
max
是选取中心之间的最大距离。
[0118]
以台风风速作为输入变量x
p
，各乡镇保额损失率作为输出变量y
j
，选取适当 的径向基函数扩展系数构建径向基神经网络保额损失率预测模型，并设置相应 的训练集及训练目标，具体是创建一个径向基函数扩展系数为1.2的径向基神经 网络，设置均方误差目标为0.001。模型选取80％的样本数据进行训练，剩余20％ 的样本数据作检验校准。模型训
练曲线及保额损失率对比图分别如图7、9所示， 根据模型训练曲线收敛程度以及数据误差的精度要求来检验得到的预测模型的 准确性，若满足要求即达到设定的均方误差目标0.001，则继续进行下一步，否 则就调整模型参数值重新构建神经网络直至满足条件为止。
[0119]
步骤5：通过预测模型预测得到不同台风风速下各乡镇保额损失率，根据预 测结果对评估地区进行乡镇级分辨率的农村住房台风灾害评估。
[0120]
通过预测模型对不同设计台风风速下各乡镇保额损失率进行预测，根据预 测结果得到台风风速影响下最大保额损失率及对应的乡镇，并生成评估报告， 评估报告包括：台风风速大小、预估保额损失和农村住房灾害分布情况。
[0121]
在一个实施例中，通过《建筑结构荷载规范》规定的宁波市10年、50年、 100年一遇的风压计算相应的设计风速，其值分别为21.91m/s、28.28m/s、 30.98m/s。通过已训练好的神经网络模型分别对设计风速下宁波市各乡镇保额损 失率进行预测，结果如图11a至图11c所示。从图中可以看出农村住房保额损失 率均随着风速的增大而增大，这意味着出现灾情的可能性增大。在100年一遇 的设计风速下，宁波地区农村住房大多会遭受较大损伤，尤其是宁波南部奉化 区、宁海县、象山县的乡镇农房保额损失率要远远高于北部乡镇。在台风风速 影响下，图中保额损失率预测值大的乡镇，其住房在台风来临时容易造成损伤， 易对财产和人员生命安全造成威胁。根据台风灾情预测结果，在台风来临前， 应急管理部门可以及时并且有针对性地进行农房加固抢修，尽可能减少因风致 倒塌造成的人员伤亡和经济损失。
[0122]
下面通过实验来验证本发明提出的方法的可行性和优越性。
[0123]
(1)神经网络模型构建
[0124]
根据已有数据样本，利用matlab软件分别建立基于bp(back propagation) 神经网络和rbf(radical basis function,rbf)神经网络的农村住房台风灾 情预估模型。其中bp神经网络设计为典型的3层网络模型。输入层数据为台风 风速，输出层数据为各乡镇保额损失率，统计数据涵盖宁波139个乡镇。确定 隐含层神经元个数为5，传递函数分别采用正切s型传递函数“tansig”、线性 传递函数“purelin”。学习训练函数采用系统默认的“trainlm”函数，并设 置训练次数为1000，训练目标为0.001，其他参数取默认值。
[0125]
rbf神经网络的构建相比bp神经网络更为简单。根据已有数据样本，通过
ꢀ“
newrb”函数创建一个径向基函数扩展系数为1.2的神经网络，设置均方误差 目标为0.001。
[0126]
(2)神经网络模型训练比较
[0127]
两种模型均选取80％的样本数据进行训练，剩余20％的样本数据作检验校准。 在训练时为了使bp神经网络更接近训练目标，需要对模型内隐含层节点数、训 练函数等相关参数进行调整，这些往往需要花费较久时间调试。相比之下，rbf 神经网络在训练过程中，通过设置可使隐含层节点数自动增加，从0个开始检 查网络的误差是否达到误差要求，直到达到误差要求或最大隐含层节点数为止。
[0128]
在训练精度为0.001时，两种模型训练曲线如图7和图8所示。由图可知， 两模型在给定条件下均收敛，但bp神经网络模型需要110步才能达到精度要求。 rbf神经网络模型只需要12步即可达到要求，训练速度明显优于bp神经网络。 另外，通过运行两种模型发现，在参数确定的情况下，rbf模型的训练结果基本 相同，而bp模型的训练结果并不次次稳定，有时会有较大偏差。
[0129]
更进一步的，bp、rbf两模型预测值与实际值对比如图9所示，并利用均方 误差值作为两模型模拟情况的评价指标，如图10所示，从图中可知，通过bp神 经网络模型预测的结果最大均方误差值为18
×
10
‑6，相比于绝对误差最大值为8
ꢀ×
10
‑6的rbf神经网络模型，精度不够高且误差范围波动较大。尽管在同一乡 镇两种方法的均方误差互有高低，但总体而言，rbf的预测值均方误差小于bp 神经网络。
[0130]
因此，上述结果说明，在相同条件下建立的rbf神经网络具有更高的预测 精度，并且训练时间和收敛速度均优于bp神经网络。因此，利用rbf神经网络 构建台风灾情预估模型比bp神经网络更具优势。
[0131]
综上所述，本发明利用rbf神经网络有效建立了从致灾因子到承灾体损失 的台风灾情评估模型，借助公共巨灾保险数据可以实现乡镇级高分辨率的农村 住房台风灾情预估，解决传统风险评估空间分辨率较低、风险度量难的问题， 精确到各乡镇、村的风险灾害预估，量化评估台风灾害风险，为后续制定台风 灾害保险政策、台风应急预案等应用提供科学依据，可有效减少因风致倒塌造 成的人员伤亡和经济损失。
[0132]
以上仅为本发明较佳的实施例，并非因此限制本发明的实施方式及保护范 围，对于本领域技术人员而言，应当能够意识到凡运用本发明说明书及图示内 容所作出的等同替换和显而易见的变化所得到的方案，均应当包含在本发明的 保护范围内。