三输入前导零预测算法的制作方法

1.本发明涉及芯片设计技术领域，具体为用于浮点乘加器的三输入前导零预测算法。


背景技术：

2.浮点乘加器(浮点乘加器的作用是计算浮点数a*b
±
c)、两输入前导零预测(两个二进制数相减在高位会产生一大堆零，此算法预测出首个一前面有多少个零然后交给后续模块移位)、前导零检测(输入为一串二进制数，直接输出二进制数首个1前面连续零的个数)
3.已有技术及其缺陷：现在已有的技术为两输入的前导零算法，在进行浮点乘加器设计的时候少一个操作数，不满足设计要求，于是对两输入前导零预测进行改进，增加一个操作数来满足设计要求。两输入前导零算法在运用到浮点乘加器中的时候至少需要一级3:2压缩器将三个操作数压缩到两个操作数才可以使用，并且前导零算法只针对减法，经过一级3:2压缩器的时候减法符号已经使数据变成补码融合在了数据中，无法使用预测算法进行预测。


技术实现要素：

4.本发明提出一种三输入前导零预测算法，采取的技术方案为：
5.一种三输入前导零预测算法，包括如下步骤：
6.s1、预设三个二进制的数分别为a、b、c，将需要预测的a、b、c三个数进行编码，生成中间变量d、e、g、h、m、n和q；
7.其中，d＝a&b&(～c)
8.e＝(a&b&c)|((a^b)&～c)
9.g＝((～a)&(～b)&(～c))|((a^b)&c)
10.h＝(～a)&(～b)&c
11.m＝a^b^c
12.n＝(a&b)|((a^b)&(～c))
13.q＝((～a)&(～b))|((a^b)&c)；
14.s2、将中间变量d、e、g、h、m、n和q输入预测编码公式，得出预测结果，f_pos和f_neg；
15.f_pos＝[gi+di]d
i+1
+m
igi+1
+[(gi+di)e
i+1
+m
ihi+1
]n
i+2
；
[0016]
f_neg＝[hi+ei][h
i+1
+g
i+1qi+2
]+g
iei+1
+[di+gi]d
i+1qi+2
+d
iei+1
；
[0017]
其中，i为二进制数的第i位，f_pos为正预测结果，f_neg为负预测结果；
[0018]
s3、将s2中f_pos和f_neg分别输入正编码树和负编码树，得出预测数的前导零数量；
[0019]
s4、根据外部的选择信号进行结果选择。
[0020]
对本发明技术方案的优选，s4中外部的选择信号为加法电路输出的符号位，当符号位为0，表示加法结果为正，选择正编码树；当符号位为1表示加法结果为负，选择负编码树。
[0021]
本发明与现有技术相比，其有益效果是：
[0022]
本发明方法，可以对三个数的减法运算(a+b-c)进行前导零的预测，可以用在浮点乘加器中和压缩器路径并行运算，缩短时序路径，以提高浮点乘加器的运行频率，实现高性能运算。
附图说明
[0023]
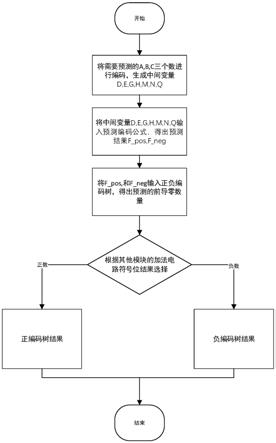
图1是本发明方法的流程框图。
[0024]
图2是本发明方法的模型图。
具体实施方式
[0025]
下面对本发明技术方案进行详细说明，但是本发明的保护范围不局限于所述实施例。
[0026]
为使本发明的内容更加明显易懂，以下结合附图1-附图2和具体实施方式做进一步的描述。
[0027]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅用以解释本发明，并不用于限定本发明。
[0028]
本发明提出的一种三输入前导零预测算法，包括如下步骤：
[0029]
s1、预设三个二进制的数分别为a、b、c，将需要预测的a、b、c三个数进行编码，生成中间变量d、e、g、h、m、n和q；
[0030]
其中，d＝a&b&(～c)
[0031]
e＝(a&b&c)|((a^b)&～c)
[0032]
g＝((～a)&(～b)&(～c))|((a^b)&c)
[0033]
h＝(～a)&(～b)&c
[0034]
m＝a^b^c
[0035]
n＝(a&b)|((a^b)&(～c))
[0036]
q＝((～a)&(～b))|((a^b)&c)；
[0037]
s2、将中间变量d、e、g、h、m、n和q输入预测编码公式，得出预测结果，f_pos和f_neg；
[0038]
f_pos＝[gi+di]d
i+1
+m
igi+1
+[(gi+di)e
i+1
+m
ihi+1
]n
i+2
；
[0039]
f_neg＝[hi+ei][h
i+1
+g
i+1qi+2
]+g
iei+1
+[di+gi]d
i+1qi+2
+d
iei+1
；
[0040]
其中，i为二进制数的第i位，f_pos为正预测结果，f_neg为负预测结果；
[0041]
s3、将s2中f_pos和f_neg分别输入正编码树和负编码树，得出预测数的前导零数量；
[0042]
s4、根据外部的选择信号进行结果选择。
[0043]
本方法，s4中外部的选择信号为加法电路输出的符号位，当符号位为0，表示加法
结果为正，选择正编码树；当符号位为1表示加法结果为负，选择负编码树。
[0044]
本实施例的方法中，拿到三个二进制数a,b,c，先产生中间变量结果，d,e,g,h,m,n,q。将中间变量输入到正编码公式和负编码公式(f_pos,f_neg)中，得出正预测结果和负预测结果。将正负预测结果输入到正负编码树进行前导零计数，最后由外部的选择信号选择正编码树的结果还是负编码树的结果。外部信号是加法电路输出的符号位，当符号位为0表示加法结果为正，选择正编码树，当符号位为1表示加法结果为负，选择负编码树。
[0045]
本实施例的方法中，中间变量结果d,e,g,h,m,n,q，各个中间变量的计算公式为本领域的已知公式，本领域技术人员已知。中间变量代表a+b-c的每一位的结果。a+b-c每一位运算完毕后有四种情况{2,1,0，-1}。d代表2，e代表1，g代表0，h代表-1，m代表[1+(-1)]，n代表[1+2]，q代表[0+(-1)],+是或的意思。
[0046]
各个中间变量的计算公式内，&是表示按位与，～是表示按位取反，|是表示按位或，^是表示按位异或；按位是对二进制数的每一位进行操作。
[0047]
本实施例方法中，正编码公式和负编码公式内，出现的结构形式比如“m
igi+1”，写在一起是按位与的意思；出现的结构形式比如“di+g
i”是表示按位或的意思。
[0048]
本实施例中，正预测编码公式f_pos＝[gi+di]d
i+1
+m
igi+1
+[(gi+di)e
i+1
+m
ihi+1
]n
i+2
；负预测编码公式f_neg＝[hi+ei][h
i+1
+g
i+1qi+2
]+g
iei+1
+[di+gi]d
i+1qi+2
+d
iei+1
；的推导过程如下：
[0049]
在浮点乘加器中，在第二拍会使用第一拍乘法的数据sum和carry，和移位后的操作数c，在第二拍的时候计算sum+carry
–
c，然后进行移位，为了提高性能，使用前导零预测算法，预测三个数运算后的结果前面零的个数提供给后面进行移位，并且预测出的零的个数有一位误差，一位误差后续再进行简单判断即可。
[0050]
本实施例提出的三个二进制的数分别为a、b、c，针对a+b-c或者c-a-b的形式进行预测预测编码公式的推导。
[0051]
设三个操作数为a、b、c，w＝a+b-c，w每一位不进位，则w的每一位wi(wi＝ai+b
i-ci)，有2,1,0，-1四种情况，故需要四个中间变量表示。三个操作数为a、b、c均为二进制的数；其中，i为二进制数的第i位。
[0052]
对w分正负进行讨论：
[0053]
当w≥0时，此时，w的最高位只可能为1或2；2表示有进位。
[0054]
1、若w＝0k2(x)
[0055]
(默认w前面有零，所以实际计算的时候操作数a,b,c前面要补一位0)
[0056]
x表示由2，1，0，-1任意组合成的数字串，0k表示连续k个0。
[0057]
(1)若x≥0，则不需要向前借位，2向前进一位，最高有效位位于第k位。
[0058]
(2)若x《0，需要向前借位，最高有效位位于第k+1位。
[0059]
因为允许带有一位误差，故总假设前导1出现在第k位，一位误差由后续模块修正。则带有一位误差的识别码为：
[0060]
wiw
i+1
＝0
i2i+1
[0061]
2、若w＝0k1(x)
[0062]
(默认w前面有零，所以实际计算的时候操作数a,b,c前面要补一位0)
[0063]
此时情况复杂，需分类讨论：
[0064]
(1)w＝0k12(x)
[0065]
(a)x不向前借位，则前导1位于第k位。
[0066]
(b)x向前借位，则前导1位于第k+1位。
[0067]
则带有一位误差的识别码为：
[0068]
wiw
i+1
＝0
i1i+12i+2
[0069]
(2)w＝0k11(x)
[0070]
x可以有三种情况，有进位、对高位无操作、有借位；当有进位的时候，前导1位于第k位。当对高位无操作时，前导1位于第k+1位。当有借位的时候前导1位于第k+1位。综上前导1位于第k位或第k+1位。
[0071]
则带有一位误差的识别码为：
[0072]
wiw
i+1
＝0
i1i+11i+2
[0073]
(3)w＝0k10(x)
[0074]
x可以有三种情况，有进位、对高位无操作、有借位。当有进位的时候，前导1位于k+1位，当对高位无操作的时候，前导1位于k+1位，当有借位的时候，前导1位于第k+2位。
[0075]
则带有一位误差的识别码为：
[0076]
wiw
i+1
＝1
i0i+1
[0077]
(4)当w＝0k1(-1)(x)时
[0078]
(a)当x为2的时候，会向前进位抵消掉-1，后面的值当不借位的时候，前导1的位置位于k+1位，当向前借位的时候，只需考虑极限的情况，后面的每一位都为-1，则向前借1位即可抵消掉后面全部的-1，所以前导1的位置位于k+2位。
[0079]
(b)当x为1时，并且后面的值向前进位，则-1被抵消掉，前导1的位置位于第k+1位，当后面的值不进位，或者有借位的时候，借位都被x的1吸收掉，所以前导1的位置位于k+2位。
[0080]
(c)当x为-1时，w＝0k1(-1)(-1)x,情况和w＝0k1(-1)(x)类似，因为经化简后w＝0k001(x)，和w＝0k01(x)相似，讨论情况的结果相似。
[0081]
所以将本讨论情况扩展为0k1(-1)m2(x)、0k1(-1)m1(x)、0k1(-1)m0(x)和0k1(-1)m四种情况。
[0082]
首先讨论这四种情况的完备性，当m为1的时候，已包含-1后面接2，1，0的情况，当后面接-1的时候，后面又可以接四种数字，2，1，0也已经包含在前三种情况里，唯一没有包含的是一直(-1)循环到末尾的情况，所以补充0k1(-1)m这一种情况就已经将w＝0k1(-1)(x)的所有情况列出。
[0083]
i)当w＝0k1(-1)m2(x)时
[0084]
当x向前有借位的时候，前导1的位置位于k+m+1的位置，当x不向前借位或者向前有进位的时候，前导1的位置位于k+1位。当m为1时，识别码为1
i-1
i+12i+2
；当m》1时，识别码为-1
i-1
i+12i+2
。综上带有一位误差的识别码为：
[0085]
wiw
i+1
＝1
i-1
i+12i+2
或-1
i-1
i+12i+2
[0086]
检测码检测的是首1位置，虽然w前面有值，但是忽略掉。
[0087]
ii)当w＝0k1(-1)m1(x)时
[0088]
当x向前有进位的时候，前导1的位置位于k+1位，当x对高位无操作，或向前有借位
的时候，前导1的位置位于k+m+1的位置。综上，带有一位误差的识别码为：
[0089]
wiw
i+1
＝1
i-1
i+11i+2
或-1
i-1
i+11i+2
[0090]
iii)当w＝0k1(-1)m0(x)时
[0091]
当x向前有进位或者对高位无操作的时候，前导1的位置位于第k+m+1的位置，当x所有位都为-1的时候，也只向前借一位就足够了，所以前导1的位置位于第k+m+2的位置。综上带有一位误差的识别码为：
[0092]
wiw
i+1
＝-1
i0i+1
[0093]
iiii)当w＝0k1(-1)m时
[0094]
结果为最后一位为1，其余位都为0，在原始数据最后补0，通过识别码-1
i0i+1
可识别出来。
[0095]
3、当0k(-1)22(x)时，化简为0k002(x)，情况和0k2(x)相同，前导1的位置在k+2或k+3位置，带有一位误差的识别码为：
[0096]
wiw
i+1
＝2
i2i+1
[0097]
注意：虽然情况和0k2(x)相同，但识别码并不相同，不能共用，因为0k2(x)的识别码使用了2前面的0位，与0k(-1)22(x)不同。
[0098]
4、当0k(-1)212(x)时，化简为0k0012(x)，情况和0k12(x)类似，所以检测码为2
i1i+12i+2
。
[0099]
5、当0k(-1)211(x)时，化简为0k0011(x)，情况和0k11(x)类似，所以检测码为2
i1i+11i+2
。
[0100]
6、当0k(-1)21(0，-1)(x)时，化简为0k001(0，-1)(x)，情况和0k10(x)，0k1(-1)(x)类似，因为0k10(x)，0k1(-1)(x)所使用的检测码不涉及0k中的0，所以检测码可以共用，所以0k(-1)21(0，-1)(x)不需要自己的检测码。
[0101]
7、当0k(-1)20(x)时，2进位将-1抵消掉，化简为0k000(x)，结果和其他情况相同，和其他情况共用检测码。
[0102]
8、当0k(-1)2(-1)(x)时，化简为0k00(-1)(x)，情况和0k(-1)(x)的情况相同，所以可以共用检测码。
[0103]
9、当0k(-1)1m2(x)时，化简为0k00m0(x)，可以和其他情况共用检测码，(x)前面的值为2检测码也可以和0k(-1)22(x)、0k(-1)212(x)、0k(-1)211(x)共用。综上，检测码可以共用。
[0104]
(检测码要保证的是正确检测出首1的位置，不能和其他情况首1前面要忽略的字符冲突。)
[0105]
由以上分析，得出w≥0时的识别前导一位置的检测码规则表表1。
[0106]
表1 w≥0时的识别前导一位置的检测码规则表
[0107]
[0108][0109]
表1中，0k代表k个0，(-1)m代表m个-1，(x)代表可取的任意值2,1,0,-1并且有任意个，并且数量不为零。
[0110]
表1中，检测码相同并没有影响，因为只要找到前导一的位置就可以。要注意的是前面本该忽略掉的数字组不能被检测到。
[0111]
检测码满足一个就代表找到前导一的位置，所以将所有检测码相或化简得：
[0112]fi
＝[0i+2i]2
i+1
+[1i+(-1)i]0
i+1
+[(0i+2i)1
i+1
+[1i+(-1)i](-1)
i+1
][2
i+2
+1
i+2
]
[0113]
为进一步化简，设d表示2，e表示1，g表示0，h表示-1，m表示[1+(-1)]，n表示[1+2]，q表示[0+(-1)]。
[0114]
最终化简结果为：
[0115]
f_pos＝[gi+di]d
i+1
+m
igi+1
+[(gi+di)e
i+1
+m
ihi+1
]n
i+2
。
[0116]
当w《0时，为方便讨论，将w取反命名为u进行讨论，u＝c-a-b；
[0117]
1、当u＝0k11(x)时，当x没有向前借位的时候，前导1的位置在第k+1位，当x全部为-2的时候，将全部的-2向前进位变成-1，则前导1的位置在k+2的位置上。所以带一位误差的检测码为q＝1
i1i+1
。
[0118]
2、当u＝0k10(0,1)(x)时，当x没有向前借位的时候，前导1的位置在第k+1位，当x全部为-2的时候仅需要向次高位借一位，所以前导零的位置在k+2位，所以带一位误差的检测码为1
i0i+10i+2
或1
i0i+11i+2
。
[0119]
3、当0k10(-1)(x)时，化简为0k011(x)，11(x)和情况1相同，所以前导一会在k+2或者k+3的位置，所以检测码为0i(-1)
i+1
。
[0120]
4、当0k10(-2)m(1,0)(x)时，化简为0
k0m
10(1,0)(x)，现只讨论极限情况，(x)不借位和(x)全部都是-2借位的情况。其他情况的前导一位置包含在两种极限情况之间。
[0121]
4.1)当不借位的时候，前导一位置在k+m+1的位置。
[0122]
4.2)当(x)全是-2，全部借位的情况，只讨论边界情况，u＝0k10(-2)m0(x)，-2向前进位变为-1，化简为u＝0
k0m
10(-1)j0，-1向高位借一位即可，则前导1的位置位于k+m+2的位置。
[0123]
综上，并且考虑m为1或者m》1的情况，检测码为(-2)i(-2)
i+11i+2
或(-2)i(-2)
i+10i+2
或0i(-2)
i+11i+2
或0i(-2)
i+10i+2
。
[0124]
5、当0k10(-2)m(-1)(x)时，根据前述4.2条的讨论，将-2向前进位，10(-2)m组合的结果为0m10，所以将原式化简为0
k0m
10(-1)(x)，进一步化简得0
k0m
011(x)，出现11(x)组合，和情况1相同，所以前导一的位置在k+m+2或k+m+3的位置。所以检测的时候检测码为(-2)i(-1)
i+1
。
[0125]
6、当0k10(-2)m时，前面会产生许多的0，只有在倒数第二位会有一个1，在u末尾扩展一个0，检测码为(-2)i(-2)
i+10i
+2。
[0126]
7、当0k1(-1)m1(x)时，化简为0
k0m
11(x)的时候，产生11(x)组合，前导1的位置和情况1一致，所以检测码为(-1)
i1i+1
。
[0127]
8、当0k1(-1)m0(0,1)(x)时，前导1的位置位于k+m+1或k+m+2位置，所以检测码为(-1)
i0i+10i+2
或(-1)
i0i+11i+2
。
[0128]
9、当0k1(-1)m0(-1)(x)时前导1的位置位于k+m+2或k+m+3的位置，所以检测码为0i(-1)
i+1
。
[0129]
10、当0k1(-1)m0(-2)j(1,0)(x)时，将-2进位为-1，化简成0k1(-1)m(-1)j0(1,0)(x)，前导1的位置位于第k+m+j+1或k+m+j+2的位置，因为j可能为1，也可能大于1，所以前导1的检测码为(-2)i(-2)
i+11i+2
或(-2)i(-2)
i+10i+2
或0i(-2)
i+11i+2
或0i(-2)
i+10i+2
。
[0130]
11、当0k1(-1)m0(-2)j(-1)(x)时，化简为0k1(-1)m(-1)j0(-1)(x)，化简为0
k0m+j
10(-1)(x)，当x全部为-2的时候，向前进位化简为0
k0m+j
1(-1)0(-1)i0，前导1的位置位于k+m+j+3位，当x不向前借位的时候，前导1的位置位于k+m+j+2位，综上，带一位误差的检测码为(-2)i(-1)
i+1
。
[0131]
12、当0k1(-1)m(-2)(x)时，化简为0
k0m
1(-2)(x)，和下面的情况共用检测码。
[0132]
13、当0k1(-2)(x)时，化简为0k00(x)，x的取值情况为{1,0,-1,-2}；
[0133]
i)当x为1的时候，情况和w《0的情况相同，和w《0所有情况共用检测码。
[0134]
ii)当x为0的时候，情况和本情况13相同，共用检测码。
[0135]
iii)当x＝-2,-1的时候，将其取反讨论，当x＝2时，w为正数，后面的(x)可以是{2,1,0,-1}，后面位数的借位不会影响其为正数。当x＝1时，后面可接{2,1,0,-1}，分成两种情况讨论。这里所述的“w为正数，”，即为，因为u是w的取反，在本情况下-2进位和1进行了抵消(公式)，所以当x为负数的时候，u是负数，将其取反讨论正好是w。
[0136]
a)当x＝1后面接{2,1,0}的时候，格式为1(2,1,0)(x)，不会影响w为正数。
[0137]
b)当x＝1后面接-1的时候为1(-1)(x)，化简为01(x)，格式又转化为1(x)形式，(x)可取的值为{2,1,0,-1}，所以即使当(x)全部为-1的时候，w依然为正，所以不会影响w为正数。
[0138]
综上，当u＝0k1(-2)(-2,-1)(x)时，u《0，即，二进制计算，-2向前进位变成-1，和1抵消，(-2，-1)的符号就决定了u的符号，所以u是负数。当进行编码树正负选择的时候，会选择正编码树的结果，所以这两种情况对结果无影响。
[0139]
由上分析，得出u＜0时的识别前导一位置的检测码规则表表2。
[0140]
表2 u＜0时的识别前导一位置的检测码规则表
[0141][0142][0143]
表2中，u取值为1,0，-1，-2，u》0，表格中(0,1)的意思是这一位可以为0，也可以为1)
[0144]
将检测码化简后结果为：
[0145]fi
＝[(-1)i+1i][(-1)
i+1
+0
i+1
[0
i+2
+(-1)
i+2
]]+0
i1i+1
+[2i+0i]2
i+1
[(-1)
i+2
+0
i+2
]+2
i1i+1
[0146]
为进一步化简，设d表示2，e表示1，g表示0，h表示-1，m表示[1+(-1)]，n表示[1+2]，q表示[0+(-1)]。
[0147]
最终化简结果为：
[0148]
f_neg＝[hi+ei][h
i+1
+g
i+1qi+2
]+g
iei+1
+[di+gi]d
i+1qi+2
+d
iei+1
[0149]
自此，三输入前导零预测的中间结果已经生成，对中间结果进行前导零检测输出最终前导零结果。
[0150]
如图1和2所示，本实施例中，正编码树、负编码树就是前导零检测模块，对预测出的结果进行前导零检测。正编码树、负编码树为本领域已知模块，本领域技术人员已知。
[0151]
如图1和2所示，a、b、c是a+b-c的三个操作数，d、e、g、h、m、n、q是中间变量，f_pos和f_neg是产生的预测结果。
[0152]
举例1
[0153]
将a,b,c三个数前面补一个0，后面补两个零，送入中间变量计算公式。(因为检测码前面默认有0，所以前面要补一个0。因为检测码是连着三位的，要保证每一位都检测到，所以要在后面补两个零)
[0154]
a＝{1’b0,6’b111100,2’b00}
[0155]
b＝{1’b0,6’b110011,2’b00}
[0156]
c＝{1’b0,6’b101010,2’b00}
[0157]
d,e,g,h,m,n,q都为9位。
[0158]
d＝a&b&(～c)//2
[0159]
e＝(a&b&c)|((a^b)&～c)//1
[0160]
g＝((～a)&(～b)&(～c))|((a^b)&c)//0
[0161]
h＝(～a)&(～b)&c//-1
[0162]
m＝a^b^c//[1+(-1)]
[0163]
n＝(a&b)|((a^b)&(～c))//[1+2]
[0164]
q＝((～a)&(～b))|((a^b)&c)//[0+(-1)]
[0165]
得到中间变量后将中间变量送入正负编码树中
[0166]
f_pos＝[gi+di]d
i+1
+m
igi+1
+[(gi+di)e
i+1
+m
ihi+1
]n
i+2
[0167]
f_neg＝[hi+ei][h
i+1
+g
i+1qi+2
]+g
iei+1
+[di+gi]d
i+1qi+2
+d
iei+1
[0168]
得出预测结果，预测结果没有后面扩的两位0，为7位。
[0169]
将预测结果送入正负编码树统计前导零个数。通过其他模块加法的符号位选择正负编码树得出最终结果。
[0170]
本例结果为正，选择正编码树结果f_pos，预测结果前导一位置正确。
[0171]
得出表中结果
[0172][0173]
举例2
[0174]
将a,b,c三个数前面补一个0，后面补两个零，送入中间变量计算公式。(因为检测码前面默认有0，所以前面要补一个0。因为检测码是连着三位的，要保证每一位都检测到，所以要在后面补两个零)
[0175]
a＝{1’b0,6’b001100,2’b00}
[0176]
b＝{1’b0,6’b100011,2’b00}
[0177]
c＝{1’b0,6’b111010,2’b00}
[0178]
d,e,g,h,m,n,q都为9位。
[0179]
d＝a&b&(～c)//2
[0180]
e＝(a&b&c)|((a^b)&～c)//1
[0181]
g＝((～a)&(～b)&(～c))|((a^b)&c)//0
[0182]
h＝(～a)&(～b)&c//-1
[0183]
m＝a^b^c//[1+(-1)]
[0184]
n＝(a&b)|((a^b)&(～c))//[1+2]
[0185]
q＝((～a)&(～b))|((a^b)&c)//[0+(-1)]
[0186]
得到中间变量后将中间变量送入正负编码树中
[0187]
f_pos＝[gi+di]d
i+1
+m
igi+1
+[(gi+di)e
i+1
+m
ihi+1
]n
i+2
[0188]
f_neg＝[hi+ei][h
i+1
+g
i+1qi+2
]+g
iei+1
+[di+gi]d
i+1qi+2
+d
iei+1
[0189]
得出预测结果，预测结果没有后面扩的两位0，为7位。
[0190]
将预测结果送入正负编码树统计前导零个数。通过其他模块加法的符号位选择正负编码树得出最终结果。
[0191]
本例结果为负，选择负编码树结果f_neg，负编码树的结果为c-a-b的前导零位置，预测结果前导一位置为最终结果前导一位置，正确。
[0192]
得出表中结果
[0193][0194][0195]
本发明未涉及部分均与现有技术相同或可采用现有技术加以实现。
[0196]
如上所述，尽管参照特定的优选实施例已经表示和表述了本发明，但其不得解释为对本发明自身的限制。在不脱离所附权利要求定义的本发明的精神和范围前提下，可对其在形式上和细节上作出各种变化。