粘弹性材料力传感器动态补偿方法和系统
1.本发明涉及传感器动态补偿技术领域,特别是涉及一种粘弹性材料力传感器动态补偿方法和系统。
背景技术:
2.小型化力传感器的敏感材料—软材料(硅橡胶、凝胶、聚合物等)因其生产工艺简单、成本低和灵敏度高而被广泛应用。然而,软材料具有高阶线性时不变特性,其表现出的粘弹性具有强烈的历史依赖性,并在阶跃激励下存在明显的蠕变现象,严重影响传感器输出的稳定性和精度;此外,软材料的固有频率和阻尼比通常很小,这使得传感器的动态响应速度较慢。
3.粘弹性材料的力学模型可采用弹簧和阻尼器的不同组合方式来描述。常用开尔文模型、麦克斯韦模型、广义开尔文模型等建立粘弹性材料在阶跃激励下的应变模型以研究其蠕变现象。一般的,模型中弹簧和阻尼器越多,对粘弹性系统的描述越精确,但也导致系统的阶数上升,大幅提升传感器系统辨识的难度和传感器的计算能力需求。
4.同时,部分研究者使用系统辨识法和零极点放置法来提升传感器的动态特性。系统辨识法将传感器视为黑盒,根据校准数据和传感器输出直接识别补偿器,可能会忽略高阶系统中低阶成分的影响,限制了带宽的扩展。而零极点放置法的补偿精度依赖于传感器动态模型的准确性,更适用于低阶最小相位系统。
5.因此,本领域亟待提供一种能够提高传感器动态测量的精度和时域跟随性能的粘弹性材料力传感器动态补偿方法或系统。
技术实现要素:
6.本发明的目的是提供一种粘弹性材料力传感器动态补偿方法和系统,能够提高传感器动态测量的精度和时域跟随性能。
7.为实现上述目的,本发明提供了如下方案:
8.一种粘弹性材料力传感器动态补偿方法,包括:
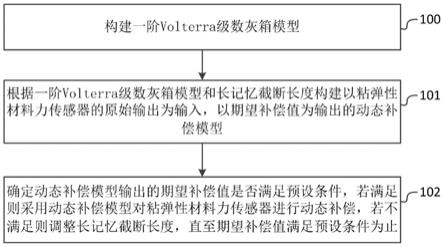
9.构建一阶volterra级数灰箱模型;所述一阶volterra级数灰箱模型为基于一阶volterra级数构建的粘弹性材料力传感器系统模型;
10.根据所述一阶volterra级数灰箱模型和长记忆截断长度构建以粘弹性材料力传感器的原始输出为输入,以期望补偿值为输出的动态补偿模型;
11.确定所述动态补偿模型输出的期望补偿值是否满足预设条件,若满足则采用所述动态补偿模型对所述粘弹性材料力传感器进行动态补偿,若不满足则调整所述长记忆截断长度,直至所述期望补偿值满足预设条件为止。
12.优选地,所述构建一阶volterra级数灰箱模型,具体包括:
13.获取粘弹性材料力传感器系统的系统增益和粘弹性材料的应变;
14.根据所述系统增益和所述粘弹性材料的应变构建所述一阶volterra级数灰箱模
型;所述一阶volterra级数灰箱模型为:
[0015][0016]
其中,m为长记忆截断长度,δc(t)为输出,k为系统增益,ε(t)为粘弹性材料的应变,σ(t-i)为记忆链接,t为采样时间,i为采样点序号,a为一阶volterra级数的参数,a=(a1,
…
,ai,
…
,am)。
[0017]
优选地,所述动态补偿模型为:
[0018][0019]
其中,y(t)为粘弹性材料力传感器的理想输出,δc(t)为粘弹性材料力传感器的原始输出,b为动态补偿模型的参数,b=(b1,
…
,bi,
…
,bm)。
[0020]
优选地,根据所述一阶volterra级数灰箱模型和长记忆截断长度构建以粘弹性材料力传感器的原始输出为输入,以期望补偿值为输出的动态补偿模型,之后还包括:
[0021]
采用所述粘弹性材料力传感器的理想输出和所述粘弹性材料力传感器的原始输出拟合确定所述动态补偿模型的参数。
[0022]
优选地,所述预设条件为:经动态补偿模型动态补偿后的粘弹性材料力传感器的输出与粘弹性材料力传感器的理想输出间的差值小于预设值。
[0023]
根据本发明提供的具体实施例,本发明公开了以下技术效果:
[0024]
本发明提供的粘弹性材料力传感器动态补偿方法,通过建立基于一阶volterra级数的传感器灰箱模型,可以准确表征传感器粘弹性及高阶线性时不变特性,并且,在不需要辨识灰箱模型的情况下,构造动态补偿模型以实现针对高阶时不变粘弹性传感系统的串联补偿,进而能够提高传感器动态测量的精度和时域跟随性能。
[0025]
对应于上述提供的粘弹性材料力传感器动态补偿方法,本发明还提供了一种粘弹性材料力传感器动态补偿系统,包括:
[0026]
第一模型构建模块,用于构建一阶volterra级数灰箱模型;所述一阶volterra级数灰箱模型为基于一阶volterra级数构建的粘弹性材料力传感器系统模型;
[0027]
第二模型构建模块,用于根据所述一阶volterra级数灰箱模型和长记忆截断长度构建以粘弹性材料力传感器的原始输出为输入,以期望补偿值为输出的动态补偿模型;
[0028]
动态补偿模块,用于确定所述动态补偿模型输出的期望补偿值是否满足预设条件,若满足则采用所述动态补偿模型对所述粘弹性材料力传感器进行动态补偿,若不满足则调整所述长记忆截断长度,直至所述期望补偿值满足预设条件为止。
[0029]
优选地,所述第一模型构建模块包括:
[0030]
获取单元,用于获取粘弹性材料力传感器系统的系统增益和粘弹性材料的应变;
[0031]
构建单元,用于根据所述系统增益和所述粘弹性材料的应变构建所述一阶volterra级数灰箱模型;所述一阶volterra级数灰箱模型为:
[0032][0033]
其中,m为长记忆截断长度,δc(t)为输出,k为系统增益,ε(t)为粘弹性材料的应
变,σ(t-i)为记忆链接,t为采样时间,i为采样点序号,a为一阶volterra级数的参数,a=(a1,
…
,ai,
…
,am)。
[0034]
优选地,还包括:
[0035]
参数确定模块,用于采用所述粘弹性材料力传感器的理想输出和所述粘弹性材料力传感器的原始输出拟合确定所述动态补偿模型的参数。
[0036]
因本发明提供的粘弹性材料力传感器动态补偿系统达到的技术效果与上述提供的粘弹性材料力传感器动态补偿系统达到的技术效果相同,故在此不再进行赘述。
附图说明
[0037]
为了更清楚地说明本发明实施例或现有技术中的技术方案,下面将对实施例中所需要使用的附图作简单地介绍,显而易见地,下面描述中的附图仅仅是本发明的一些实施例,对于本领域普通技术人员来讲,在不付出创造性劳动性的前提下,还可以根据这些附图获得其他的附图。
[0038]
图1为本发明提供的粘弹性材料力传感器动态补偿方法的流程图;
[0039]
图2为本发明提供的粘弹性材料力传感器动态补偿方法的实施架构图;
[0040]
图3为本发明实施例提供的电容式力传感器测量原理图;
[0041]
图4为本发明实施例提供的传感器动态补偿流程图;
[0042]
图5为本发明实施例提供的补偿效果示意图;
[0043]
图6为本发明提供的粘弹性材料力传感器动态补偿系统的结构示意图。
具体实施方式
[0044]
下面将结合本发明实施例中的附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。基于本发明中的实施例,本领域普通技术人员在没有做出创造性劳动前提下所获得的所有其他实施例,都属于本发明保护的范围。
[0045]
本发明的目的是提供一种粘弹性材料力传感器动态补偿方法和系统,能够提高传感器动态测量的精度和时域跟随性能。
[0046]
为使本发明的上述目的、特征和优点能够更加明显易懂,下面结合附图和具体实施方式对本发明作进一步详细的说明。
[0047]
如图1所示,本发明提供的粘弹性材料力传感器动态补偿方法,包括:
[0048]
步骤100:构建一阶volterra级数灰箱模型。一阶volterra级数灰箱模型为基于一阶volterra级数构建的粘弹性材料力传感器系统模型。其中,构建得到的一阶volterra级数灰箱模型为:
[0049][0050]
其中,m为长记忆截断长度,δc(t)为输出,k为系统增益,ε(t)为粘弹性材料的应变,σ(t-i)为记忆链接,t为采样时间,i为采样点序号,a为一阶volterra级数的参数,a=(a1,
…
,ai,
…
,am)。
[0051]
步骤101:根据一阶volterra级数灰箱模型和长记忆截断长度构建以粘弹性材料
力传感器的原始输出为输入,以期望补偿值为输出的动态补偿模型。其中,构建得到的动态补偿模型为:
[0052][0053]
其中,y(t)为粘弹性材料力传感器的理想输出,δc(t)为粘弹性材料力传感器的原始输出,b为动态补偿模型的参数,b=(b1,
…
,bi,
…
,bm)。
[0054]
步骤102:确定动态补偿模型输出的期望补偿值是否满足预设条件,若满足则采用动态补偿模型对粘弹性材料力传感器进行动态补偿,若不满足则调整长记忆截断长度,直至期望补偿值满足预设条件为止。其中,本发明采用的预设条件可以依据实际需求进行设定,例如,可以将预设条件设置为:经动态补偿模型动态补偿后的粘弹性材料力传感器的输出与粘弹性材料力传感器的理想输出间的差值小于预设值。
[0055]
为了进一步提高动态补偿的精确性,本发明在构建得到动态补偿模型,之后还采用粘弹性材料力传感器的理想输出和粘弹性材料力传感器的原始输出拟合确定动态补偿模型的参数。
[0056]
针对基于软材料等粘弹性材料制作的力传感器,其输出的模拟电信号通常和软敏感材料的应变存在线性关系。以电容式力传感器为例,该类型传感器通常使用极板变间距原理测量正压力,使用极板变面积原理测量测量剪切力,如图3所示。下面基于电容式力传感器的测量原理对本发明上述提供的粘弹性材料力传感器动态补偿方法的具体实施过程和达到的技术效果进行说明。
[0057]
在本实施例中,粘弹性材料力传感器动态补偿方法的具体实施流程如图2所示。
[0058]
在测量单元中,应变与电容变化量存在以下线性关系:
[0059][0060]
式中,d0为敏感材料层厚度,εr为敏感材料层相对介电常数,ε0为真空介电常数,s为正压力测量单元电极平面的正对面积,l为垂直于所检测剪切力方向的电极平面的长度,δcn(t)和δcs(t)分别是在拉压力εn(t)和剪切力εs(t)作用下的电容变化量。
[0061]
显然,在传感器量程内,传感器的输入和介质层应变为线性关系。因此,不失一般性,传感器的输出可以表示为:
[0062]
δc(t)=kε(t)
[0063]
如果材料为理想弹性体,则上式中ε(t)可以描述为:
[0064][0065]
其中,e
ideal
和g
ideal
分别是理想弹性体的弹性模量和剪切模量。
[0066]
然而,软材料并不是理想的弹性体,软材料的粘弹性使得应变ε(t)在恒定应力下
不断变化,影响传感器的稳定性和精度。因此,准确表征应力(蠕变)下应变的连续变化是实现传感器精确测量的关键。
[0067]
以广义kelvin模型为例,若系统输入为σ(t),则传感器系统可被描述为:
[0068][0069]
式中,j(t)为广义kelvin模型中的蠕变柔量:
[0070][0071]
其中,k作为系统增益,表示应变与电容输出间的线性关系。t为传感器的采样时间,i为采样点的序号。从公式(3)和(4)可以看出,基于软材料的力传感器的输出是历史相关的,导致了蠕变现象,其粘性环节也会导致传感器反应迟缓。
[0072]
广义开尔文模型描述的软材料粘弹性系统是一个n+1阶线性时不变系统。通常,随着弹性和粘性单元数量的增加,模型对粘弹性系统的描述越准确,系统的阶数也越高。但对应的补偿方法需要在频域推导传感器的零极点并设计相应的补偿器,难以处理上述的高阶系统。
[0073]
但是,在时域上,如果能去掉式(3)中的历史依赖环节,则补偿后的系统输出有望接近理想的伺服系统,无需对高阶系统的零极点进行复杂的识别。预期补偿结果表示为:
[0074]
y(t)=ka0σ(t)
ꢀꢀ
(5)
[0075]
其中,a0表示时间t处应力和应变之间的增益。
[0076]
为了达到公式(5)所示的理想补偿结果,需要消除公式(3)中的历史记忆链接σ(t-t)~σ(t-nt)。然而蠕变柔量和应力都是与时间t相关的函数,复杂粘弹性模型(如式(4))的卷积计算(如式(3))限制了补偿器的设计。
[0077]
一阶volterra级数可以描述线性时不变系统,并随着记忆长度的增加提高系统的描述精度。在实际当中,采用拥有长记忆环节的一阶volterra级数表示,尽可能精确的表征传感器粘弹性及高阶线性时不变特性,同时避免多元件建模给模型带来的复杂性。
[0078]
在任意时刻t,j(t)~j(it)可以看作是n个固定系数。因此,为了有效表征高阶线性时不变粘弹性系统的历史依赖性,引入具有长记忆特性的一阶volterra级数来描述基于软材料的传感器系统,即:
[0079][0080]
其中,m是模型的长记忆截断长度,a=(a1,
…
,ai,
…
,am)是一阶volterra级数的参数。
[0081]
同时,随着长记忆截断参数m的增加,传感器系统的描述精度同步上升。
[0082]
从式(5)和式(6)可以看出,如果补偿器能够抵消一阶volterra级数灰箱模型中历史记忆链接σ(t-1)~σ(t-m)的所有部分,则可以实现高效的系统补偿来抵消传感器系统的高阶粘弹性环节,消除蠕变并提升响应速度。此时,补偿器的预期输出为:
[0083][0084]
其中,y(t)为传感器的理想输出。
[0085]
然而,在测量系统的实际使用中,补偿器无法直接获取应力信息。根据公式(6),应从电容信息中获取历史应力信息。因此,基于一阶volterra级数灰箱模型及其长记忆截断长度m,建立输出为期望补偿值、输入为传感器原始输出的动态补偿模型,动态补偿模型形式为:
[0086][0087]
其中,b=(b1,
…
,bi,
…
,bm)是补偿器的参数,δc(t)-δc(t-i)可在传感器系统中测得,式(8)可展开为类似于式(7)的与应力σ(t)~σ(t-m)有关的形式。若存在b使式(7)和式(8)成立,则该补偿器可达到预期的补偿效果。
[0088]
此时将δc(t)-δc(t-m)采用一阶volterra灰箱模型的形式展开,如下:
[0089][0090]
此时理想补偿输出展开成:
[0091][0092]
为了得到理想的补偿效果,希望公式(6)中σ(t)的系数不为零,但历史依赖环节σ(t-1)~σ(t-m)的系数都为零或接近零,使得补偿后的系统是或接近随动系统,达到良好的补偿效果。因此,令列出下列方程:
[0093][0094]
式(11)进一步可以表示为:
[0095][0096]
整理后得:
[0097][0098]
其中,a=(a1,
…
,ai,
…
,am)为一阶volterra级数灰箱模型中描述传感器粘弹性特点和高阶线性时不变特点的长记忆参数,b=(b1,
…
,bi,
…
,bm)为补偿器待拟合参数。
[0099]
对于不同系统参数a,至少存在最小二乘解b使上式成立,即使实际输出接近理想随动输出,因此采用标定的理想输出y(t)与原始输出δc(t)拟合补偿器。
[0100]
基于上述内容,在实际拟合参数b时,将理想输出y(t)构造为校准数据。根据式(7),理想输出y(t)越接近理想传感系统的输出,y(t)-δc(t)越接近系统中需要消除的历史依赖部分,并且补偿器的效果越好。因此,采用阶跃响应法对传感器进行动态标定,对传感器各轴施加阶跃激励,记录传感器未经动态补偿的原始输出δc(t)用于补偿器参数辨识。构建理想输出y(t)为:
[0101][0102]
其中,δc0为理想阶跃激励下传感器长时间后的稳定输出。
[0103]
根据一阶volterra灰箱模型的阶跃激励时间t0和截断长度m,得到理想输出y(t0)~y(t0+m-1),对应的电容输出δc(t
0-m)~δc(t0+m-1)根据式(8)得到收集结果为:
[0104][0105]
进一步,令y(t0)-δc(t0)=d(t0),f(t0,i)=δc(t0)-δc(t
0-i),式(15)可表示为:
[0106][0107]
如式(16)所示,其中,f
mm
为m阶方阵,b
m1
为m行1列的矩阵,d
m1
为m行1列的矩阵。可以通过lu分解、qr分解等方法求解线性方程组得出参数b。因此,利用校准数据y(t)和传感器原始输出δc(t)拟合补偿器中的参数b(式12),可以获得有效的系统补偿器来消除蠕变并提高系统的响应时间。拟合过程如图4所示。
[0108]
此外,长记忆截断长度m越长,一阶volterra级数描述传感器的精度越高,补偿器(公式12)的效果越好。但考虑到传感器嵌入式系统的计算能力,补偿器的截断长度会受到限制。一般情况下,选择2倍原始输出δc(t)上升时间与采样时间t的比值作为长记忆截断长度m拟合补偿器。随后验证补偿效果并调整补偿器的截断长度(如图4所示),尤其是补偿后的传感器的阶跃响应调整时间和过冲。
[0109]
最后,将解得的参数b写入传感器嵌入式系统的程序中,得到的补偿效果如图5所示,图5中δc(t)为传感器原始数据,y(t)为经过补偿后传感器对阶跃激励的响应。
[0110]
基于上述描述,本实施例提供的粘弹性材料力传感器动态补偿方法,首先,建立基于一阶volterra级数的传感器灰箱模型,表征传感器中粘弹性力学特征与高阶线性时不变特点,并通过volterra长记忆截断长度提升模型的精度。其次,在不需要辨识灰箱模型的情况下,构造补偿器,即基于一阶volterra级数灰箱模型表征的传感器系统,并以随动系统为目标,推导构建在线补偿器以实现针对高阶时不变粘弹性传感系统的串联补偿。然后,对传感器进行阶跃响应实验以获取补偿器参数辨识的动态标定实验数据,进而基于标定数据实现在线补偿器的参数拟合。最后,采用拟合后的基于一阶volterra级数灰箱模型的动态补偿器对传感器的测量输出进行动态补偿,从而消除蠕变并有效提高传感器的时频域动态性能。
[0111]
对应于上述提供的粘弹性材料力传感器动态补偿方法,本发明还提供了一种粘弹性材料力传感器动态补偿系统,如图6所示,该系统包括:
[0112]
第一模型构建模块600,用于构建一阶volterra级数灰箱模型。一阶volterra级数灰箱模型为基于一阶volterra级数构建的粘弹性材料力传感器系统模型。
[0113]
第二模型构建模块601,用于根据一阶volterra级数灰箱模型和长记忆截断长度构建以粘弹性材料力传感器的原始输出为输入,以期望补偿值为输出的动态补偿模型。
[0114]
动态补偿模块602,用于确定动态补偿模型输出的期望补偿值是否满足预设条件,若满足则采用动态补偿模型对粘弹性材料力传感器进行动态补偿,若不满足则调整长记忆截断长度,直至期望补偿值满足预设条件为止。
[0115]
其中,第一模型构建模块600包括:获取单元和构建单元。
[0116]
获取单元,用于获取粘弹性材料力传感器系统的系统增益和粘弹性材料的应变。
[0117]
构建单元,用于根据系统增益和粘弹性材料的应变构建一阶volterra级数灰箱模型。一阶volterra级数灰箱模型为:
[0118][0119]
其中,m为长记忆截断长度,δc(t)为输出,k为系统增益,ε(t)为粘弹性材料的应变,σ(t-i)为记忆链接,t为采样时间,i为采样点序号,a为一阶volterra级数的参数,a=(a1,
…
,ai,
…
,am)。
[0120]
进一步为了提高补偿精度,本发明上述提供的系统还优选包括:参数确定模块。该参数确定模块用于采用粘弹性材料力传感器的理想输出和粘弹性材料力传感器的原始输出拟合确定动态补偿模型的参数。
[0121]
本说明书中各个实施例采用递进的方式描述,每个实施例重点说明的都是与其他实施例的不同之处,各个实施例之间相同相似部分互相参见即可。对于实施例公开的系统而言,由于其与实施例公开的方法相对应,所以描述的比较简单,相关之处参见方法部分说明即可。
[0122]
本文中应用了具体个例对本发明的原理及实施方式进行了阐述,以上实施例的说明只是用于帮助理解本发明的方法及其核心思想;同时,对于本领域的一般技术人员,依据本发明的思想,在具体实施方式及应用范围上均会有改变之处。综上所述,本说明书内容不应理解为对本发明的限制。
相关技术
网友询问留言
已有0条留言
- 还没有人留言评论。精彩留言会获得点赞!
1