基于KD树算法求解气动软体机器人逆解建模方法

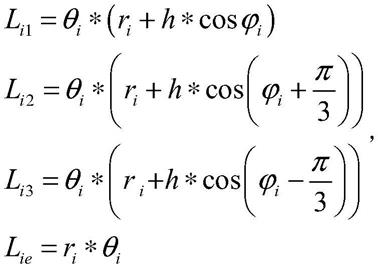
基于kd树算法求解气动软体机器人逆解建模方法
技术领域
1.本发明具体涉及一种基于kd树算法求解气动软体机器人逆解建模方法。


背景技术：

2.随着科学技术的发展，机器人也渐渐的由传统的制造业向其他领域延伸，并且在军事、医学、教育等领域逐渐普及应用。但是传统的刚性结构机器人越来越难以满足人们对机器功能多样化的需求，于是相关研究人员从自然界中获取灵感，渐渐开发出了仿生机器人。与传统的刚性机器人相比，仿生软体机器人具有较高的自由度，可以在非结构的环境中进行移动。并且在躲避障碍物方面软体机器人也要比传统刚性机器人拥有更灵活的优势。
3.但是与传统的刚性机器人相比，软体机器人的求解也更加复杂，特别是对软体机器人的逆解，即由工作空间反求虚拟关节空间再由此关联到驱动空间上面。具体的就是已知待要抓取的目标的坐标，反向求解出虚拟关节空间中的虚拟关节空间变量：偏转角α、弯曲角θ、曲率半径r。然后再根据虚拟关节空间变量与驱动空间变量的映射关系去得知驱动空间机械臂长度的变化量，完成对整个机器人逆解的求解过程。


技术实现要素：

4.针对现有技术存在的不足，本发明的目的在于提供一种基于kd树算法求解气动软体机器人逆解建模方法。
5.为实现上述目的，本发明提供了如下技术方案：
6.一种基于kd树算法求解气动软体机器人逆解建模方法，其包括以下步骤：
7.步骤一、根据软体机器人的驱动结构，做出分段常曲率假设、最短长度假设及偏转角共面假设，利用驱动空间、虚拟关节空间、工作空间两个映射关系建立正向运动学公式；
8.步骤二、根据正向运动学公式，利用驱动空间与虚拟关节空间、虚拟关节空间与工作空间两个映射关系来随机生成大量数据；
9.步骤三、利用kd树分割步骤二中生成的数据中关于空间坐标部分建立kd树，并将空间坐标与虚拟关节变量相关联；
10.步骤四、将软体机器人的工作空间的待抓取的目标坐标代入，并寻找最近点，查找与之相关联的虚拟关节变量；
11.步骤五、将虚拟关节变量与驱动空间变量通过转换公式转换，得到软体机器人的逆解。
12.步骤一中的最短长度假设，即波纹管中始终有一腔体保持最大负压状态，同时假设波纹管先由驱动空间压力p的变化，根据压力与长度的对应关系可以得出各个波纹管腔体的长度。
13.步骤一中，通过前期测量获得驱动空间与虚拟关节空间之间的映射关系。
14.步骤三中，将分割后的数据建立kd树，每一个子节点都与虚拟关节空间的偏转角弯曲角θ、曲率半径ri值一一对应。
15.步骤四中，利用kd树建立的数据模型，按照先后顺序，在xyz三个维度中比较，然后进入子树，不断迭代，直到找出最小值。
16.所述最小值满足小于设定的设定值，若是出现多个值，就是满足多解，然后可以根据实际应用的场景，放弃一部分解。
17.步骤一中：在分段常曲率假设下，通过将长度随腔体气压变化时，第i段的弯曲角θi及偏转角的变化关系映射到笛卡尔坐标系下，获得软体机器人每个波纹管长度：
[0018][0019]
其中l
ie
为三波纹管所在圆弧的圆心中心线的弧长，
[0020]
通过上述关系可以获得
[0021][0022][0023][0024]
并通过建立d-h表，获得软体机器人第i段上下底面坐标系的齐次变换矩阵
[0025][0026]
其中cθi＝cosθi，sθi＝sinθi，i为i段软体机器人，因此由链式法则可知由末端坐标系到基座坐标系变换矩阵如下：
[0027][0028]
并完成正向运动学建模。
[0029]
本发明的有益效果：本发明利用kd树算法解决求解过程大量三维数据的匹配问题，提出了利用数据库查找，求出符合范围误差范围的最近点，并根据工作空间到虚拟关节空间，再到驱动空间的两种映射关系求出逆解。
附图说明
[0030]
图1为求解正运动学流程图；
[0031]
图2为求解逆运动学流程图；
具体实施方式
[0032]
下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明的一部分实施例，而不是全部的实施例。基于本发明中的实施例，本领域普通技术人员在没有作出创造性劳动前提下所获得的所有其他实施例，都属于本发明保护的范围。
[0033]
本发明提供了一种基于kd树算法求解气动软体机器人逆解建模方法，其包括以下步骤：
[0034]
步骤一、根据软体机器人的驱动结构，做出分段常曲率假设、最短长度假设及偏转角共面假设，利用驱动空间、虚拟关节空间、工作空间两个映射关系建立正向运动学公式；其中最短长度假设，假设软体机器人弯曲时每段至少有一腔体处于最大负压状态，并以该假设获取软体机器人的曲率半径ri，
[0035][0036]
步骤二、根据正向运动学公式，利用驱动空间与虚拟关节空间、虚拟关节空间与工作空间两个映射关系来随机生成大量数据；
[0037]
步骤三、利用kd树分割步骤二中生成的数据中关于空间坐标部分，并利用空间坐标建立kd树，并将空间坐标与虚拟关节变量相关联；
[0038]
步骤四、将软体机器人的工作空间的待抓取的目标坐标代入，并寻找最近点，查找与之相关联的虚拟关节变量；
[0039]
步骤五、将虚拟关节变量与驱动空间变量通过转换公式转换，得到软体机器人的逆解。
[0040]
实施例1
[0041]
本实施例以气动软体波纹管机械臂为例，该机械臂主要有三部分构成，上段弯曲部分，下段弯曲部分，抓手部分。其中上，下段弯曲部分只负责弯曲。抓手部分负责抓取目标点的物体。
[0042]
步骤1、利用软体机器人结构，建立正向运动学公式，其中根据软体机器人，做出常曲率假设、最短长度假设，利用驱动空间、虚拟关节空间、工作空间两个映射关系可以推导出正向运动学公式；
[0043]
基于常曲率模型的假设即弯曲段曲率不变假设和最短长度假设，最短长度假设即波纹管中始终有一腔体保持最大负压状态，同时假设波纹管先由驱动空间压力p的变化，根据压力与长度的对应关系可以得出各个波纹管腔体的长度。得到相关的虚拟关节控件变量：偏转角两个弯曲角θ1，θ2、曲率半径r。三波纹管中心线的长度为le＝l1+l2+l3，弯曲角、偏转角和曲率半径求解公式如下：
[0044][0045]
其中，l
ij
为波纹管第i段第j个的长度，ri为第i段曲率半径，θi为第i段弯曲角，h为波纹度直径，建立三个波纹管公式，并求出偏转角弯曲角θi、曲率半径ri：
[0046][0047][0048][0049]
建立d-h表，因此软体机器人第i段上下底面坐标系的齐次变换矩阵如下：
[0050][0051]
其中cθi＝cosθi，sθi＝sinθi，i为i段软体机器人，因此由链式法则可知由末端坐标系到基座坐标系变换矩阵如下：
[0052][0053]
步骤2、根据上述步骤1中建立的正向运动学模型，由模型中推导出的驱动空间、虚拟关节空间、工作空间两个映射关系来随机生成大量数据；
[0054]
步骤3：利用kd树对步骤2生成的工作空间内的大量数据进行分割，并将分割后的数据建立kd树，每一个子节点都与虚拟关节空间的偏转角弯曲角θ、曲率半径ri值一一对应。
[0055]
步骤4：搜索工作空间中的目标坐标与步骤3建立的kd树的空间坐标距离最近的几点，在误差允许的情况下选出最优解。将最优解对应的虚拟关节变量返回。
[0056]
步骤5：由返回的虚拟关节变量带入模型，找出驱动空间压力值。完成机器人逆解。
[0057]
而对于线驱动软体机器人就是根据不同线的长度产生产生不同的力矩，使软体机器人弯曲。气压驱动软体机器人就是根据不同压强使软体机械臂弯曲。还有无模型控制，纯粹靠计算机感知软体机器人行动轨迹，并记录下来。拉线软体机器人和气动软体机器人流程是一样的。
[0058]
实施例不应视为对本发明的限制，但任何基于本发明的精神所作的改进，都应在本发明的保护范围之内。