混凝土运输罐车动态调度方法与流程

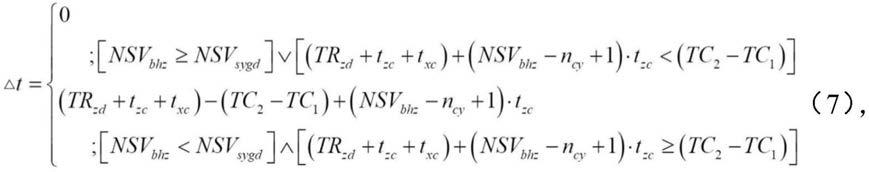
1.本发明涉及建筑施工技术领域，具体涉及一种混凝土运输罐车动态调度方法。


背景技术：

2.工程项目施工中，混凝土用量巨大，需要依靠罐车将混凝土从拌合站运送至施工现场，而由于施工工期紧、任务重、施工单位缺少科学合理的运输车调度安排，造成施工中混凝土调度混乱，浪费严重。


技术实现要素：

3.为克服现有技术所存在的缺陷，现提供一种混凝土运输罐车动态调度方法，以解决工程项目施工中混凝土调度混乱，浪费严重的问题。
4.为实现上述目的，提供一种混凝土运输罐车动态调度方法，包括以下步骤：
5.以标准粒子群算法模型作为混凝土运输罐车的静态调度模型，将等待时间作为目标函数，所述等待时间包括每个工点的等待时间、罐车的等待时间、工点的最长等待时间及罐车的最长等待时间、所有工点的累计等待时间和所有罐车的累计等待时间，其中，以工点的最长等待时间作为所述目标函数的主控因素，以总等待时间作为所述目标函数的控制因素，以施工单位的总累计等待时间作为所述目标函数的影响因素；
6.调取所述静态调度模型，同时确定调度过程计算参数以计算获取动态调度方案，所述调度过程计算参数包括第一辆车的发车时间、非第一辆车的发车时间和工点及罐车的等待时间，所述第一辆车的发车时间(ti1)：
[0007][0008]
式(1)中，t
bhz
为拌合站开工时间；tc为最早开工工点的开工时间；t
zc
为罐车装车所需时间；t
ar
为最早开工时间且罐车单次循环所需最短时间；
△
t为根据最早开工和次早开工的时间及个数、罐车最大等待时间等因素修正的时间；
[0009]
所述非第一辆车的发车时间(tim)：
[0010][0011]
式(2)中，tim为安排的第m个罐车的发车时间；tb
m-1
为安排的第m-1个罐车返回拌合站的时间；tbfm为ti
m-1
之后所有在运输途中的罐车最快返回拌合站的时间；nsvc
bhz
为ti
m-1
之后拌合站当前拥有的罐车数量；
[0012]
所述工点等待时间(tam)：
[0013]
tam＝tim+trgi＝tagc
i,n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)，
[0014]
式(3)中，tam为拌和站发出的第m个罐车到达工点的时间；tagc
i,n
为第n个罐车到达工点i的时间；
[0015]
所述罐车等待时间(tdm)：
[0016][0017]
式(4)中，tdm为拌和站发出的第m个罐车的等待时间；tlagc
i,n-1
为第n-1个罐车离开工点i的时间；tagc
i,n
为第n个罐车到达工点i的时间；nsvai为工点i安排过车辆的个数。
[0018]
进一步的，所述标准粒子群算法模型为：
[0019][0020][0021]
式(5)和(6)中，i＝1,2,
……
,n(种群大小)；w为惯性权重；,n(种群大小)；w为惯性权重；为粒子i在第t代的速度及位置方向向量；gbest
t
为第t代的粒子i的个体最优及全体粒子的全局最优；c1、c2为个体认知权重及全体社会权重；r1、r2为两个均匀分布在[0,1]之间的随机d维矢量参数。
[0022]
进一步的，若最早开工工点唯一(即n
zy
＝1)，次早开工工点有n
cy
个且n
cy
》1时，
△
t以下式计算：
[0023][0024]
式(1)中，“∧”表且，交集；“∨”表或，并集；nsv
bhz
为拌合站用于罐车总数，nsv
sygd
为工点需要的罐车所有工点累计需要车辆总数，tr
zd
为所有工点中单次循环的最短时间，tr
zc
为所有工点中单次循环的最长时间，t
zc
为装车时间和t
xc
为卸料时间。
[0025]
进一步的，若最早开工工点有多个，次早开工工点有一个时，
△
t以下式计算：
[0026][0027]
进一步的，若最早开工工点有多个，次早开工工点有多个时，
△
t以下式计算：
[0028][0029]
本发明的有益效果在于，本发明的混凝土运输罐车动态调度方法基于标准粒子群算法建议静态混凝土运输罐车调度模型，结合工程实际提出了适用于罐车动态调度问题的权重系数模型、粒子越界处理方法，可提高混凝土拌合站工作效率、降低工程质量风险。
具体实施方式
[0030]
下面结合实施例对本技术作进一步的详细说明。可以理解的是，此处所描述的具体实施例仅仅用于解释相关发明，而非对该发明的限定。
[0031]
需要说明的是，在不冲突的情况下，本技术中的实施例及实施例中的特征可以相互组合。下面将结合实施例来详细说明本技术。
[0032]
参照所示，本发明提供了一种混凝土运输罐车动态调度方法，包括以下步骤：
[0033]
s1：以标准粒子群算法模型作为混凝土运输罐车的静态调度模型，以等待时间作为目标函数，计算获取静态调度方案，其中，所述等待时间包括每个工点的等待时间、罐车的等待时间、工点的最长等待时间及罐车的最长等待时间、所有工点的累计等待时间和所有罐车的累计等待时间，以工点的最长等待时间作为所述目标函数的主控因素，以总等待时间作为所述目标函数的控制因素，以施工单位的总累计等待时间作为所述目标函数的影响因素.
[0034]
s2：重新调取所述静态调度模型，并确定调度过程计算参数以计算获取动态调度方案，所述计算参数包括第一辆车的发车时间、非第一辆车的发车时间和工点及罐车的等待时间，所述第一辆车的发车时间(ti1)：
[0035][0036]
式(1)中，t
bhz
为拌合站开工时间；tc为最早开工工点的开工时间；t
zc
为罐车装车所需时间；t
ar
为最早开工时间且罐车单次循环所需最短时间；
△
t为根据最早开工和次早开工的时间及个数、罐车最大等待时间等因素修正的时间；
[0037]
所述非第一辆车的发车时间(tim)：
[0038][0039]
式(2)中，tim为安排的第m个罐车的发车时间；tb
m-1
为安排的第m-1个罐车返回拌合站的时间；tbfm为ti
m-1
之后所有在运输途中的罐车最快返回拌合站的时间；nsvc
bhz
为ti
m-1
之后拌合站当前拥有的罐车数量；
[0040]
所述工点等待时间(tam)：
[0041]
tam＝tim+trgi＝tagc
i,n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)，
[0042]
式(3)中，tam为拌和站发出的第m个罐车到达工点的时间；tagc
i,n
为第n个罐车到达工点i的时间；
[0043]
所述罐车等待时间(tdm)：
[0044][0045]
式(4)中，tdm为拌和站发出的第m个罐车的等待时间；tlagc
i,n-1
为第n-1个罐车离开工点i的时间；tagc
i,n
为第n个罐车到达工点i的时间；nsvai为工点i安排过车辆的个数。
[0046]
本发明的混凝土运输罐车动态调度方法基于标准粒子群算法建议静态混凝土运输罐车调度模型，结合工程实际提出了适用于罐车动态调度问题的权重系数模型、粒子越界处理方法，可提高混凝土拌合站工作效率、降低工程质量风险。
[0047]
在本实施例中，标准粒子群算法模型为：
[0048][0049][0050]
式(5)和(6)中，i＝1,2,
……
,n(种群大小)；w为惯性权重；,n(种群大小)；w为惯性权重；为粒子i在第t代的速度及位置方向向量；gbest
t
为第t代的粒子i的个体最优及全体粒子的全局最优；c1、c2为个体认知权重及全体社会权重；r1、r2为两个均匀分布在[0,1]之间的随机d维矢量参数。
[0051]
其中，静态调度模型个体最优与全局最优的确定，需要在智能算法计算过程中，需给出目标函数，且目标函数的合理性直接影响着收敛结果的精度。针对调度问题，目标函数一般取等待时间，即等待时间越短则该解越优。针对本发明解决的工程调度问题，一般存在6个等待时间，首先，工点每完成一车灌注，存在2个等待时间，即工点的等待时间tgdi和罐车的等待时间tgci(下角标表示完成i车灌注时对应的等待时间)；其次，对于所有工点及罐车都存在一个最长等待时间tmax
gd
和tmax
gc
；相应的存在2个累计等待时间，即所有工点的累计等待时间ts
gd
和所有罐车的累计等待时间ts
gc
。具体计算见下式：
[0052][0053]
在本实施例中，目标函数需满足所有工点及罐车的最长等待时间(tmax
gd
和tmax
gc
)均不大于其他方案，同时施工单位的总累计等待时间(ts
gd
)应小于1.2倍其他方案的总累计等待时间(其中，1.2是修正系数。如前所述，是为了保证将所有可能的最优解都考虑到解集里)。
[0054]
从而，对于每一个粒子来说，粒子i的个体最优解可通过以下算法流程一得到，具体的，算法流程一：
[0055][0056]
对于整个粒子群而言，全局最优解可通过以下算法流程二得到，具体的，算法流程二：
[0057][0058]
在混凝土调度过程中常常出现临时增加或取消订单，增加或减少可用罐车数量的动态变化情况。变化后需要对静态调度安排打乱重新形成新的调度单，且需保证已经完成的订单不被打乱(包括工点混凝土浇筑已完成情况、可用罐车信息等)。因突发情况的不可预知性，直接建立动态调度的计算模型，难度大且不易实现。然而，通过不同时刻调用静态计算模型可方便快捷地实现动态调度。
[0059]
在静态调度模型的基础上，将调度过程可用车辆分成两部分，一部分为现阶段拌和站可用的车辆数nsv1
bhz
；第二部分为拌合站发出且未返回至拌合站的车辆数nsv2
bhz
，以及每辆车返回至拌合站的预计时刻tbsk(k∈[1,nsv2
bhz
])。
[0060]
在重新调取静态调度模型时，拌合站开工时刻t
bhz
应为当前时刻t
cur
；工点的开工时刻tci应为每个工点在途中的车辆的最后浇筑完成时刻tlagc
i,k
(如果该工点有多辆车在途中，那么就是最后一辆车的浇筑完成时刻；如果该工点没有在途中的车辆，即当前时刻还未开工，那么开工时刻不变)；工点i需要的罐车总数nsvgdi根据实际浇筑混凝土量进行调整(实际浇筑混凝土根据重新计算时刻之前派往该工点的所有罐车完成的浇筑量)，按下式(2-1)计算。
[0061]
[0062]
式中，vci为工点i混凝土总需求量，量纲l3；vt为罐车的容量，量纲l3。
[0063]
此外，静态调度模型计算过程中，运输途中车辆最快返回至拌和时刻tbfm需根据tbsk进行修正，按式(2-2)计算。
[0064][0065]
式中，为拌合站可用的nsv1
bhz
车辆中最快返回至拌合站时刻；为拌合站可用的nsv2
bhz
车辆中最快返回至拌合站时刻。且不同罐车返回至拌合站的时刻tbj依据式(1)进行更新。
[0066]
车辆编号nv的确定：首先根据在途中的nsv2
bhz
个车辆的返回至拌和站时间，确定派往最早开工工点的发车时刻前返回至拌合站的车辆数nsv3
bhz
；然后根据发车顺序，首先对最先发出的nsv1
bhz
+nsv3
bhz
个车辆依次编号；最后根据剩余在途中车辆的最快返回时间依次编号。按下式计算。
[0067][0068]
关于拌合站当前拥有的罐车数量nsvc
bhz
，拌合站每发出一辆车，则拌合站拥有车辆数相应较少一个。同时，每返回拌合站一辆车，则拌合站拥有车辆数相应增加一个。此外，需根据途中车辆返回至拌合站时刻tbsk对nsvc
bhz
进行修正，具体计算流程三：
[0069][0070]
此外，一般拌合站都配置双机拌和，即可同时对两辆罐车进行装料。根据拌和机的空置情况对罐车的发车时间根据下式(2-4)进行修正，
[0071][0072]
式(2-4)中，ti
′m为修正后的拌合站发出的第m个车的发车时间；n
mo
为当前拌合机的占用个数。
[0073]
若仅有一个工点需要混凝土，按式(2-1)计算即可，且δt＝0。若有多个最早和次早开工工点，第一辆车的发往工点选择应为罐车单次循环时间最短的工点。然后，需根据拌合站可用车辆总数nsv
bhz
、所有工点累计需要车辆总数nsv
sygd
、所有工点中单次循环的最长
时间tr
zc
及最短时间tr
zd
、装车时间和卸料时间t
xc
确定修正时间δt。根据最早、次早工点的个数(nse
gd
、nsc
gd
)进行分别讨论。
[0074]
若最早开工工点唯一(即n
zy
＝1)，次早开工工点有n
cy
个(n
cy
》0)。当n
cy
＝1时，如果最早开工工点最快返回拌合站的时间早于次早开工的时间，那么可不进行第一辆车发车时间的修正(表明在次早开工时间开工前，已有罐车返回拌合站)；如果拌和站拥有罐车数大于最早开工和次早开工工点需求量车辆的总和，那也可不进行时间修正；当拌合站拥有车辆数不足，且最快返回拌合站的车辆晚于次要开工时间，则需将发车时间提前最早开工tc1与次早开工tc2的时间差值。当n
cy
》1时，可根据n
cy
个数的不同进行调整，具体可按下式(7)计算：
[0075][0076]
式(1)中，“∧”表且，交集；“∨”表或，并集；nsv
bhz
为拌合站用于罐车总数，nsv
sygd
为工点需要的罐车所有工点累计需要车辆总数，tr
zd
为所有工点中单次循环的最短时间，tr
zc
为所有工点中单次循环的最长时间，t
zc
为装车时间和t
xc
为卸料时间。
[0077]
若最早开工工点有多个(即n
zy
》1)，次早开工工点有一个(即n
cy
＝1)时，
△
t以下式(8)计算：
[0078][0079]
若最早开工工点有多个，次早开工工点有多个时，
△
t以下式计算：
[0080][0081]
另外，由于混凝土初凝时间的限制，混凝土罐车最长等待时间不能超过给定的允许最长等待时间tw
gc
。因此，需根据初凝时间限制，计算修正时间δt
′
，按下式(10)计算：
[0082]
[0083]
最后，对修正时间δt和δt
′
进行比较，取两者中的较小者。
[0084]
根据车辆选择的工点进行讨论。若车辆选择的工点i已经安排过车辆(即，此车不是该工点第一辆车)，根据拌合站当前拥有的罐车数量计算该车的发车时间，见下式(2)：
[0085][0086]
式中，tim表示安排的第m个车辆的发车时间；tb
m-1
表示安排的第m-1个车辆返回拌合站的时间；tbfm表示ti
m-1
之后所有在运输途中的罐车最快返回拌合站的时间；nsvc
bhz
表示ti
m-1
之后拌合站当前拥有的罐车数量。
[0087]
若车辆选择的工点i没有安排过车辆(即，此车是该工点第一辆车)，那么根据该工点的开工时间tci、拌和站到工点所需的时间trgi及装车时间推算发车时间按下式(12)计算：
[0088]
tim＝tc
i-trg
i-t
zc
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(12)，
[0089]
式中，trgi为拌合站到工点i的所需的时间(工点i为第m个罐车车选择的工点)。
[0090]
如果式(12)计算结果不大于式(2)结果(即，正常发车时间晚于以该工点开工时间推算的发车时间)，按式(2)计算发车时间发车即可。如果式(12)计算结果远大于式(2)结果(即，工点i的开工时间很晚)，此时若按式(2)结果发车，罐车的等待时间很长，有可能超过混凝土的初凝时间，而且罐车的利用率很低；若按式(12)结果发车，会影响后续的发车，较长时间内罐车在拌和站等待派单，造成罐车的浪费，同时影响其他工点的施工。因此，为避免局部最优和产生过多无效解，如果式(12)计算结果大于式(2)结果时，需重新进行工点的选择。并根据工点的个数ns
gd
、式(12)与(2)结果的时间差δtm和平均装料时间，经过大量数据试算后，重新工点选择的次数nag可按下式(13)计算：
[0091][0092]
此外，本发明根据δtm与所有罐车可能发出后的时间进行比较，细化可能的发车时间。
[0093]
1)如果δtm《t
zc
，那么按照公式(2)计算。
[0094]
2)如果δtm≥t
zc
且δtm《ns
gd
·
(0.8
·
t
zc
)+tmgdi，那么需重新选择工点，然后再重新计算，直至达到重新计算次数的上限(重新计算的次数根据公式(13)确定)。若δtm≤tw
gc
按式(12)计算tim；若δtm＞tw
gc
根据再根据式(14)计算tim。
[0095][0096]
式中，nsvgdi为工点需要的罐车数量；tmgdi为工点i允许的最长等待时间。
[0097]
3)如果δtm≥t
zc
且δtm≥ns
gd
·
(0.8
·
t
zc
)+twgdi。同样需重新选择工点，然后再
重新计算，直至达到重新计算次数的上限(重新计算的次数根据公式(13)确定)。若δtm≤tw
gc
按式(2)计算tim；若δtm＞tw
gc
根据式(14)计算tim。
[0098]
(3)工点及罐车的等待时间
[0099]
确定了罐车的发车时间后，根据罐车从拌合站到达工点的时间(该时间可根据地图实时数据计算，即考虑了路况情况、一般车速、距离、天气等情况)，可确定罐车到达工点的时间，见下式(3)：
[0100]
tam＝tim+trgi＝tagc
i,n
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)，
[0101]
式中，tam为拌和站发出的第m个车到达工点的时间；tagc
i,n
为第n个罐车到达工点i的时间。
[0102]
罐车开始浇筑的时间需考虑是否有罐车在浇筑或排队。因此，先计算罐车的等待时间，按下式(4)计算：
[0103][0104]
式中，tdm为拌和站发出的第m个罐车的等待时间；tlagc
i,n-1
为第n-1个罐车离开工点i的时间；tagc
i,n
为第n个罐车到达工点i的时间；nsvai为工点i安排过车辆的个数。
[0105]
如果罐车等待时间tdm大于等于零，表明罐车有等待，施工单位无等待；如果罐车等待时间tdm小于零，表明罐车无等待，施工单位有等待。按下式(15)计算：
[0106][0107]
式中，tdm为拌和站发出的第m个罐车离开工点时工点的等待时间；tdgc
i,n
为第n个离开工点i的罐车的等待时间；tdgd
i,n
为工点i第n个罐车离开时的工点的等待时间。
[0108]
那么，工点i罐车及工点的总等待时间按下式(16)计算。所有工点及罐车的累计等待时间按式(10)计算。
[0109][0110]
工点开始浇筑时间、罐车离开工点时间、罐车返回到拌合站的计算详见式(17)：
[0111]
tsagc
i,n
＝tagc
i,n
+tdgc
i,n
,tlagc
i,n
＝tsagc
i,n
+t
xc
,trbgc
i,n
＝tlagc
i,n
+trbiꢀꢀ
(17)，
[0112]
式中，tsagc
i,n
为第n个到达工点i的罐车的开始浇筑时间；tlagc
i,n
为第n个到达工点i的罐车浇筑完成后离开工点的时间；trbgc
i,n
为第n个到达工点i的罐车离开工点后返回到拌合站的时间；trbi为罐车从工点i返回到拌合站所需的时间(根据地图实时数据查询得到)。
[0113]
以下以一具体算例演示动态调度方案。
[0114]
假设有三个工点需要混凝土，分别为工点a、b、c，相应参数见表1。
[0115]
表1、各工点相应计算参数
[0116][0117]
拌合站现有罐车数量为10辆，罐车容量为8m3，拌合站平均装车时间为5分钟、平均卸料时间为10分钟。计算中分别取个体认知权重c1和全体社会权重c2为2.5和1.45；粒子群大小取为50，迭代次数取为600；拌合站为双机下料拌和；拌合站开工时刻为07:30。
[0118]
计算结果见下表2动态调度方案。所有工点累计等待时间ts
gd
＝73分钟，工点最长等待时间是24分钟(第18次发车)，所有罐车累计等待时间ts
gc
＝473分钟；工点a的工点最长等待时间tmgdi＝20分钟、罐车最长等待时间tmgci＝30分钟，工点btmgdi＝24分钟、tmgci＝23分钟，工点c tmgdi＝10分钟、tmgci＝26分钟。以上均满足施工要求。
[0119]
从发车时间tim可以看出，当拌合站拥有车辆充足时每隔5分钟发车一次；当选择工点开工时刻较晚时(m＝6)，模型会自动匹配更为合适的发车时间，而没有选择7:54发车(这样会增加罐车的等待时间)；同理，当选择了不同的工点且为该工点第一次安排车辆时(m＝8，25)，根据该工点的开工时刻进行了修正调整。当拌和站没有可用车辆时(如第10次发车之后)，优化模型会根据车辆返回至拌合站的时间而确定，如8号车(m＝17)较7号车(m＝18)先返回至拌合站，故第17次发车安排10号车且发车时刻与返回拌合站时刻相同；同样的，第20、21次等也是根据罐车返回至拌合站时刻进行安排车辆。
[0120]
表2、动态调度方案
[0121]
序号m工点itimtamtdmtlagc
i,n
trbgc
i,nnv
1a7:398:1008:208:3512a7:398:10108:308:4523a7:448:15158:408:5534a7:448:15258:509:0545a7:498:20309:09:1556b8:449:1009:209:3867b8:449:10109:309:4878a8:499:20-209:309:4589a8:499:20109:409:55910a8:549:25159:5010:051011b8:549:20109:409:58112a8:599:302010:010:15213a8:599:303010:1010:25314b9:049:30109:5010:08415a9:159:462410:2010:35516a9:3810:091110:3010:45617a(4)9:4510:161410:4010:55818b9:4810:14-2410:2410:427
19b9:5510:21310:3410:52920b9:5810:241010:4411:02121b10:0510:311310:5411:121022b10:0810:342011:411:22423b10:1510:412311:1411:32224b10:2510:512311:2411:42325c10:3511:12-211:2211:45526c10:4211:19311:3211:55727c10:4511:221011:4212:05628c10:5211:291311:5212:15929b10:5511:21311:3411:528
[0122]
续表2、动态调度方案
[0123]
序号m工点itimtamtdmtlagc
i,n
trbgc
i,nnv
30b11:0211:28611:4412:02131c11:1211:49312:212:251032c11:2211:59312:1212:35433b11:3211:58-1412:812:26234b11:4212:08012:1812:36335c11:4512:22-1012:3212:55536c11:5212:29312:4213:05837b11:5512:21-312:3112:49738b(6)12:0212:28312:4112:59139c12:0512:42012:5213:15640c12:1512:52013:213:25941c12:2513:02013:1213:351042c12:2613:03913:2213:45243c12:3513:121013:3213:55444c12:3613:131913:4214:05345c12:4913:261613:5214:15746c12:5513:322014:214:25547c(6)12:5913:362614:1214:351
[0124]
以上描述仅为本技术的较佳实施例以及对所运用技术原理的说明。本领域技术人员应当理解，本技术中所涉及的发明范围，并不限于上述技术特征的特定组合而成的技术方案，同时也应涵盖在不脱离所述发明构思的情况下，由上述技术特征或其等同特征进行任意组合而形成的其它技术方案。例如上述特征与本技术中公开的(但不限于)具有类似功能的技术特征进行互相替换而形成的技术方案。