一种欠饱和储层煤层气井生产边界定量预测的计算方法

1.本发明属于煤层气开发利用技术领域，具体涉及一种欠饱和储层煤层气井生产边界定量预测的计算方法。


背景技术：

2.由于煤层气独特的富集机理和压力衰竭的开发方式，压降漏斗传播精细描述一直是煤层气开发的核心问题。压降漏斗在传播过程中要经历不同的渗流阶段，具体可以分为不稳态流阶段、稳态流阶段和拟稳态流阶段。渗流阶段的划分主要取决于外边界条件，即煤层气井的生产边界。依据生产现场的实际情况，生产边界可以分为井间压力干扰边界和伤害边界：对于低渗欠饱和煤储层，通常采用井网开发模式，即在一定区域内进行井组布井开发，实现多井间的压力协同下降，因此对应的生产边界为两井之间压降漏斗共同波及的区域，即井间压力干扰边界；对于生产过程中受到不合理因素影响的煤层气井，如不合理的工程施工、排采制度等，压降漏斗无法波及到远井区域而只能在井筒附近一定区域内降压，因此该区域对应的生产边界为伤害边界。
3.当前对生产边界的研究仍然具有一定的局限性：对于井间压力干扰边界，生产现场普遍存在一种误区，即认为两口邻井具有相同的压降漏斗传播形态，从而简单估计井间压力干扰边界为井间距的一半，但实际压降漏斗受地质、工程和排采等多因素的影响，不同煤层气井的压力传播具有特殊性，因此对生产边界不切实际的简单估计会对压降漏斗传播造成很大的误差；对于伤害边界，当前主要利用试井、数值模拟等手段进行预测储层堵塞位置，而这些手段存在测量范围较小、受人为因素影响较强的缺点，都无法获得较为准确的结果，此外生产现场在解决储层伤害问题时常采用一般性的解堵措施而无法实现针对性的方案设计，很容易对储层造成二次伤害；此外，当前已有的数学模型进行边界预测时缺乏考虑动态孔隙度、含水饱和度等因素的影响，使预测结果存在较明显偏差。
4.综上所述，当前仍缺乏一种考虑储层动态特征的煤层气井生产边界精确预测的计算方法，是煤层气高效开发的一个亟待解决的问题。


技术实现要素：

5.本发明为了解决现有技术中的不足之处，提供了一种完全定量化的煤层气井生产边界预测的计算方法。本方法从压力状态方程和物质平衡方程出发，结合煤储层孔隙度、含水饱和度的动态变化，考虑水力压裂对压力传播的影响，建立煤层气井生产边界定量预测模型，并通过编写计算流程实现数据的精细化计算，最终完成实际生产现场应用。
6.为达到上述目的，本发明提出的一种欠饱和储层煤层气井生产边界定量预测的计算方法包括以下步骤：(1)计算方法的构建基于以下基础假设条件：地层流体为气/水两相，气体为理想气体，水为微可压缩流体，流体在地层中的瞬时流动视为一系列稳态流动的集合；储层孔隙度和含水饱和度在煤层气开发过程中发生动态变化；
(2)基于吸附气的等温吸附解吸方程和游离气在孔隙中的动态变化推导煤中气相物质平衡方程，考虑地层压缩性以及动态含水饱和度推导水相物质平衡方程，采用保角变换方式建立水力压裂裂缝控制的气/水压力状态方程，将气/水相的物质平衡方程和压力状态方程相结合，建立欠饱和储层煤层气井压降漏斗传播预测模型，该模型内边界为实际井底流压，外边界为瞬时稳态流的定压边界和封闭边界，其中排水区的外边界压力为储层初始压力，解吸区的外边界压力为临界解吸压力；(3)编写模型的计算流程：代入某一生产时间的生产数据，假设解吸半径和排水半径，在欠饱和储层煤层气井压降漏斗传播预测模型中分别计算对应的累积产气量和累积产水量，并对比计算结果与实际的累积产气量和累积产水量之间的误差，采用迭代法不断优化假设值，直至误差达到合理的精度，最终确定优化后的解吸半径和排水半径为实际值；(4)代入完整的生产数据并重复步骤3，绘制生产阶段内解吸半径和排水半径的动态曲线，当两条曲线相交于一点，则确定该半径为欠饱和储层煤层气井的生产边界范围。
7.步骤(1)中所给出的依据动态孔隙度和动态含水饱和度模型，绘制煤层气生产过程中煤储层孔隙度和含水饱和度的动态变化曲线，具体包括以下假设：煤储层为双重孔隙介质，煤基质内的微小孔为气体主要赋存空间，割理裂隙为流体的主要运移空间，煤储层内流体可分为气相和水相，气体为理想气体，水为微可压缩流体，流体在地层中的瞬时流动视为一系列稳态流动的集合；储层孔隙度和含水饱和度在煤层气开发过程中发生动态变化：欠饱和煤储层以临界解吸压力为界，煤储层压力传播被划分为气相解吸区和水相排水区，在这两个区域内储层孔隙度动态变化的机理不同：在排水区内煤储层受有效应力效应的作用导致孔隙被压实，孔隙度降低；而在解吸区内由于煤层气从煤基质表面解吸出来，孔隙度同时受有效应力效应的伤害作用和基质收缩效应的恢复作用。
8.进一步地，不同区域内煤储层动态孔隙度可以表示为：式中，是储层初始孔隙度，无量纲；是排水区内动态孔隙度，无量纲；是解吸区内动态孔隙度，无量纲；是储层压力为临界解吸压力对应的孔隙度，mpa；pg是气相压力状态方程，mpa；pw是水相压力状态方程，mpa；pi是初始储层压力，mpa；p
cd
是临界解吸压力，mpa；p
l
是朗格缪尔压力，mpa；ε
max
是最大体积应变，无量纲；cf是煤岩压缩系数，mpa-1
，随储层压力变化而发生动态变化，可用以下动态方程表示：cf＝0.0026
×
p
n2-0.0252
×
pn+0.1631
ꢀꢀꢀꢀꢀꢀꢀ
(2)
9.进一步地，煤层气解吸不仅会导致储层孔隙度的变化，还会占据一部分孔隙体积，使孔隙中的地层水排出，因此地层的含水饱和度与储层压力之间符合以下关系：其中，a＝wgmr(cf+cg+cd)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)b＝wgmr(cf+cg)+cf+cwꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)c＝wgmr+1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
式中，pn和p
n+1
分别代表第n和n+1步的储层微元压力，mpa；对应的s
wn
和s
wn+1
分别代表第n和n+1步的含水饱和度，无量纲；sw为动态含水饱和度，无量纲；cw是水的压缩系数，mpa-1
；cd是解吸压缩系数，mpa-1
；p
sc
为标准状态下压力，mpa；z
sc
为标准状态下气体偏差因子，无量纲；t
sc
为标准状态下温度，k；z为储层条件下偏差因子,无量纲；t为储层温度，k；v
l
为朗格缪尔体积，m3/t；ρ为储层密度，t/m3；wgmr是气水两相的流度比，无量纲；s
wc
为束缚水饱和度，无量纲；k
rg*
为束缚水含水饱和度下的气相相对渗透率，无量纲；l和m分别为气相和水相corey指数，无量纲；μg和μw分别为气相粘度和水相粘度，mpa
·
s；cg是气体压缩系数，mpa-1
，由于气体为理想气体，z＝1，且气体压缩系数可以表示为cg＝1/pn。
10.基于煤储层物质平衡方程和气/水相压力状态方程，结合水力压裂对压力传播的影响，引用动态孔隙度和动态含水饱和度模型，建立欠饱和储层煤层气井压降漏斗传播预测模型，具体为：当储层压力大于临界解吸压力时，煤层气井生产阶段为单相水流阶段，此时排水区内水相压力状态方程可以表示为：当压力降低至临界解吸压力以下时，煤层气井生产阶段为气水两相流阶段，解吸区内气相压力状态方程可以用压力平方的方式表示为：随着煤层气的解吸，解吸区范围逐渐增加，排水区内边界条件随着解吸半径的增加而增加，因此水相压力状态方程进一步转化如下。
11.进一步地，上述气/水相压力状态方程适用于无压裂缝的径向渗流，但低渗透煤储层通常采用水力压裂等人工措施提高储层渗透率，水力压裂缝沿主应力方向延伸会导致整体压降呈椭圆型向远井区域传播，因此为方便计算采用保角变换法将椭圆域z(x,y)转换为线性域ζ(ξ,η)，气相和水相的压力状态方程可以对应表述为：线性域ζ(ξ,η)，气相和水相的压力状态方程可以对应表述为：式中，p
wf
是井底流压，mpa；lf是压裂裂缝半长，m；r
wf
是井筒半径，m；ri是排水半径，
m；r
cd
是解吸半径，m；r是压力传播半径，m；ξ
wf
是线性域中的井筒半径，与排水半径和解吸半径相比是无穷小量，设定为0，无量纲；ξi是线性域中的排水半径，无量纲；ξ
cd
是线性域中的解吸半径，无量纲。
12.煤储层物质平衡方程同样可分为气相物质平衡方程和水相物质平衡方程，对于气相物质平衡方程中累积产气量等于煤层气的解吸量加上初始游离气量减去剩余在孔隙中的煤层气量，可以表示为：为：为：对于水相物质平衡方程，分为排水区的产水和解吸区的产水，不同区域的产水机理不同：在排水区内孔隙度降低和水压缩性弹性膨胀导致产水，可以表示为：解吸区内的产水还来源于气体解吸导致的孔隙内含水饱和度的降低，因此解吸区内产水可以表示为：式中，g
p
是地面条件下累积产气量，m3；w
p1
是排水区产水量，m3；w
p2
是解吸区产水量，m3；s
wi
是初始含水饱和度，无量纲；h为煤层厚度，m；bg是气体体积系数，无量纲；b
gi
是初始气体体积系数，无量纲；bw是地层水体积系数，由于地层水为微可压缩流体，设定为1，无量纲；v为压降漏斗波及到的煤储层体积，根据jacobian矩阵将其转化为线性域的波及体积。
13.通过引入煤层气开发过程中动态孔隙度和含水饱和度，结合煤层气不同排采阶段的压力状态方程和物质平衡方程并积分，即可获得压力传播模型：的压力状态方程和物质平衡方程并积分，即可获得压力传播模型：
14.进一步地，编写模型的计算流程，代入某一生产时间的生产数据，通过假设解吸半径和排水半径，在欠饱和储层煤层气井压降漏斗传播预测模型中分别计算对应的累积产气量和累积产水量，并对比计算结果与实际的累积产气量和累积产水量之间的误差，采用迭代法不断优化假设值，直至误差达到合理的精度，最终确定优化后的解吸半径和排水半径为实际值，具体包括以下步骤：
(1)厘定煤层气储层动态特征：将上述定义的煤层气井地质参数代入动态模型中，分别刻画煤储层动态孔隙度和动态含水饱和度与储层压力之间的关系，并将动态曲线应用于后续计算流程中；(2)确定模型计算使用的基础数学方法：由于地质参数和生产数据如井底流压和累积气/水产量是已知量，而排水半径和解吸半径是未知量，因此采用迭代算法进行计算，通过假设未知量代入该方法计算累积气/水产量，不断优化假设值直到计算结果与实际生产数据之间的误差小于1％，定义为合理精度；(3)计算单相水流阶段的排水半径：代入实际生产数据，当井底流压大于临界解吸压力时，假定一个排水半径ξi值，代入模型中刻画排水区内压降漏斗动态特征并且计算累积产水量w
p1
，若计算结果w
p1
与实际累积产水量w
preal
之间的误差达到合理精度，则该假设值对应为实际排水半径，否则假设另一个排水半径重新计算；(4)计算气水两相流阶段的排水半径和解吸半径：代入实际生产数据，当井底流压小于临界解吸压力时，首先假设解吸半径ξ
cd
，代入模型中刻画解吸区内气相压降漏斗动态特征并且计算累积产气量g
p
，通过不断优化假设值直到计算结果g
p
与实际累积产气量g
preal
之间的误差达到合理精度；其次基于解吸半径ξ
cd
和气相压降漏斗计算解吸区内的产水量w
p2
；最后假设排水区内排水半径ξi，持续优化假设值直到计算得到的排水区内产水量和解吸区内产水量之和(w
p1
+w
p2
)与实际累积产水量w
preal
之间的误差达到合理精度；(5)将线性域中计算结果转化为椭圆域中：为了直观地获得椭圆域中压力传播形态特征，分别定义xi和yi、x
cd
和y
cd
为椭圆域中排水区、解吸区的最大半轴长和最小半轴长，遵循：遵循：进一步地，代入完整的生产数据并重复上述步骤，绘制生产阶段内解吸半径和排水半径的动态曲线，当两条曲线相交于一点，则确定该半径为欠饱和储层煤层气井的生产边界范围，具体为：将完整的生产数据代入计算流程中，绘制生产阶段内解吸半径和排水半径的动态曲线，随着煤层气的不断产出，解吸半径曲线逐渐增加，而对于排水半径，由于生产边界是待解值，因此模型中无法定义拟稳态流压力状态方程，导致计算的排水半径曲线出现先增加后减小的形态，当排水半径曲线与解吸半径曲线相交于一点时，交点对应的范围为煤层气井的生产边界。
15.采用上述技术方案，本发明具有以下技术效果：(1)通过引入煤层气储层动态孔隙度、含水饱和度模型，结合不同区域内气相/水相压力状态方程和物质平衡方程，考虑水力压裂对压降漏斗传播的影响，建立了欠饱和储层煤层气井生产边界定量预测模型，并通过编制计算流程，完成计算方法的建立。(2)通过所建立的方法，刻画排水半径和解吸半径动态曲线，最终实现煤层气井生产边界的预测，如井网开发模式下井间压力干扰边界以及不合理开发条件下煤储层伤害边界。(3)基于该计算方法进行压力传播的敏感性分析，厘定储层动态孔隙度、动态含水
饱和度对生产边界预测的影响，验证该计算方法的先进性和实用性。
附图说明
16.图1欠饱和储层煤层气井生产边界定量预测计算方法；图2计算流程示意图；图3案例井a实际排采曲线图；图4案例井b实际排采曲线；图5两口案例井含水饱和度动态曲线；图6两口案例井孔隙度动态曲线；图7井a排水半径/解吸半径计算结果图；图8井b排水半径/解吸半径计算结果图；图9井a排水半径/解吸半径线性域实际动态传播图；图10井b排水半径/解吸半径线性域实际动态传播图；图11井a排水半径/解吸半径椭圆域实际动态传播图；图12井b排水半径/解吸半径椭圆域实际动态传播图；图13含水饱和度对压力传播计算结果敏感性分析图。
具体实施方式
17.为使本发明的目的、技术方案和优点更加清楚，下面将结合附图对本发明实施方式作进一步详细描述。
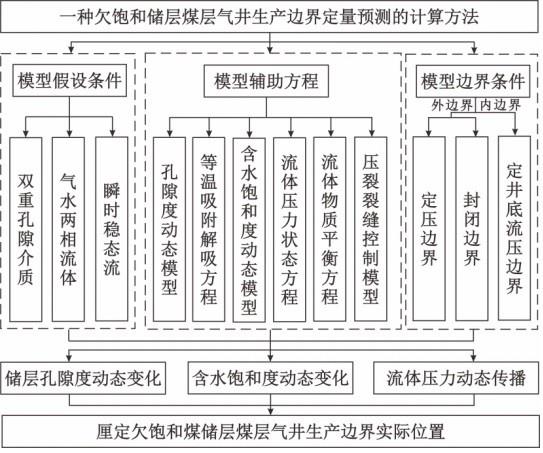
18.由于煤层气压力衰竭式的开发方式，煤层气区块多采用井网部署开发，压降漏斗传播可以在多井之间形成压力干扰，有利于储层协同降压；此外生产过程中常存在不合理的工程施工、排采制度等，煤储层会受到不可逆转的堵塞，即为伤害边界。生产边界的存在会改变储层内流体的渗流状态，因此需要对生产边界进行精细计算和表征。图1为本发明所提供的欠饱和储层煤层气井生产边界的定量预测计算方法，该方法包括：(1)计算方法的构建基于以下基础假设条件：地层流体为气/水两相，气体为理想气体，水为微可压缩流体，流体在地层中的瞬时流动视为一系列稳态流动的集合；储层孔隙度和含水饱和度在煤层气开发过程中发生动态变化；(2)基于吸附气的等温吸附解吸方程和游离气在孔隙中的动态变化推导煤中气相物质平衡方程，考虑地层压缩性以及动态含水饱和度推导水相物质平衡方程，采用保角变换方式建立水力压裂裂缝控制的气/水压力状态方程，将气/水相的物质平衡方程和压力状态方程相结合，建立欠饱和储层煤层气井压降漏斗传播预测模型，该模型内边界为实际井底流压，外边界为瞬时稳态流的定压边界和封闭边界，其中排水区的外边界压力为储层初始压力，解吸区的外边界压力为临界解吸压力；(3)编写模型的计算流程：代入某一生产时间的生产数据，假设解吸半径和排水半径，在欠饱和储层煤层气井压降漏斗传播预测模型中分别计算对应的累积产气量和累积产水量，并对比计算结果与实际的累积产气量和累积产水量之间的误差，采用迭代法不断优化假设值，直至误差达到合理的精度，最终确定优化后的解吸半径和排水半径为实际值；(4)代入完整的生产数据并重复步骤3，绘制生产阶段内解吸半径和排水半径的动态曲线，当两条曲线相交于一点，则确定该半径为欠饱和储层煤层气井的生产边界范围。
19.依据动态孔隙度和动态含水饱和度模型，绘制煤层气生产过程中煤储层孔隙度和含水饱和度的动态变化曲线，具体包括以下假设：煤储层为双重孔隙介质，煤基质内的微小孔为气体主要赋存空间，割理裂隙为流体的主要运移空间，煤储层内流体可分为气相和水相，气体为理想气体，水为微可压缩流体，流体在地层中的瞬时流动视为一系列稳态流动的集合；储层孔隙度和含水饱和度在煤层气开发过程中发生动态变化：欠饱和煤储层以临界解吸压力为界，煤储层压力传播被划分为气相解吸区和水相排水区，在这两个区域内储层孔隙度动态变化的机理不同：在排水区内煤储层受有效应力效应的作用导致孔隙被压实，孔隙度降低；而在解吸区内由于煤层气从煤基质表面解吸出来，孔隙度同时受有效应力效应的伤害作用和基质收缩效应的恢复作用，不同区域内煤储层动态孔隙度可以表示为：式中，是储层初始孔隙度，无量纲；是排水区内动态孔隙度，无量纲；是解吸区内动态孔隙度，无量纲；是储层压力为临界解吸压力对应的孔隙度，mpa；pg是气相压力状态方程，mpa；pw是水相压力状态方程，mpa；pi是初始储层压力，mpa；p
cd
是临界解吸压力，mpa；p
l
是朗格缪尔压力，mpa；ε
max
是最大体积应变，无量纲；cf是煤岩压缩系数，mpa-1
，随储层压力变化而发生动态变化，可用以下动态方程表示：cf＝0.0026
×
p
n2-0.0252
×
pn+0.1631
ꢀꢀꢀꢀꢀꢀꢀ
(25)此外煤层气解吸不仅会导致储层孔隙度的变化，还会占据一部分孔隙体积，使孔隙中的地层水排出，因此地层的含水饱和度与储层压力之间符合以下关系：其中，a＝wgmr(cf+cg+cd)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(27)b＝wgmr(cf+cg)+cf+cwꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(28)c＝wgmr+1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(29)(29)式中，pn和p
n+1
分别代表第n和n+1步的储层微元压力，mpa；对应的s
wn
和s
wn+1
分别代表第n和n+1步的含水饱和度，无量纲；sw为动态含水饱和度，无量纲；cw是水的压缩系数，mpa-1
；cd是解吸压缩系数，mpa-1
；p
sc
为标准状态下压力，mpa；z
sc
为标准状态下气体偏差因子，无量纲；t
sc
为标准状态下温度，k；z为储层条件下偏差因子,无量纲；t为储层温度，k；v
l
为朗格缪尔体积，m3/t；ρ为储层密度，t/m3；wgmr是气水两相的流度比，无量纲；s
wc
为束缚水饱和度，无量纲；k
rg*
为束缚水含水饱和度下的气相相对渗透率，无量纲；l和m分别为气相和水相corey指数，无量纲；μg和μw分别为气相粘度和水相粘度，mpa
·
s；cg是气体压缩系数，mpa-1
，由于气体为理想气体，z＝1，且气体压缩系数可以表示为cg＝1/pn。
20.基于煤储层物质平衡方程和气/水相压力状态方程，结合水力压裂对压力传播的
影响，引用动态孔隙度和动态含水饱和度模型，建立欠饱和储层煤层气井压降漏斗传播预测模型，具体为：当储层压力大于临界解吸压力时，煤层气井生产阶段为单相水流阶段，此时排水区内水相压力状态方程可以表示为：当压力降低至临界解吸压力以下时，煤层气井生产阶段为气水两相流阶段，解吸区内气相压力状态方程可以用压力平方的方式表示为：随着煤层气的解吸，解吸区范围逐渐增加，排水区内边界条件随着解吸半径的增加而增加，因此水相压力状态方程进一步转化为：上述气/水相压力状态方程适用于无压裂缝的径向渗流，但低渗透煤储层通常采用水力压裂等人工措施提高储层渗透率，水力压裂缝沿主应力方向延伸会导致整体压降呈椭圆型向远井区域传播，因此为方便计算采用保角变换法将椭圆域z(x,y)转换为线性域ζ(ξ,η)，气相和水相的压力状态方程可以对应表述为：为：式中，p
wf
是井底流压，mpa；lf是压裂裂缝半长，m；r
wf
是井筒半径，m；ri是排水半径，m；r
cd
是解吸半径，m；r是压力传播半径，m；ξ
wf
是线性域中的井筒半径，与排水半径和解吸半径相比是无穷小量，设定为0，无量纲；ξi是线性域中的排水半径，无量纲；ξ
cd
是线性域中的解吸半径，无量纲。
21.煤储层物质平衡方程同样可分为气相物质平衡方程和水相物质平衡方程，对于气相物质平衡方程中累积产气量等于煤层气的解吸量加上初始游离气量减去剩余在孔隙中的煤层气量，可以表示为：的煤层气量，可以表示为：的煤层气量，可以表示为：对于水相物质平衡方程，分为排水区的产水和解吸区的产水，不同区域的产水机理不同：在排水区内孔隙度降低和水压缩性弹性膨胀导致产水，可以表示为：
解吸区内的产水还来源于气体解吸导致的孔隙内含水饱和度的降低，因此解吸区内产水可以表示为：式中，g
p
是地面条件下累积产气量，m3；w
p1
是排水区产水量，m3；w
p2
是解吸区产水量，m3；s
wi
是初始含水饱和度，无量纲；h为煤层厚度，m；bg是气体体积系数，无量纲；b
gi
是初始气体体积系数，无量纲；bw是地层水体积系数，由于地层水为微可压缩流体，设定为1，无量纲；v为压降漏斗波及到的煤储层体积，根据jacobian矩阵将其转化为线性域的波及体积：通过引入煤层气开发过程中动态孔隙度和含水饱和度，结合煤层气不同排采阶段的压力状态方程和物质平衡方程并积分，即可获得压力传播模型：的压力状态方程和物质平衡方程并积分，即可获得压力传播模型：
22.如图2所示编写该计算方法的计算流程，代入某一生产时间的生产数据，通过假设解吸半径和排水半径，在欠饱和储层煤层气井压降漏斗传播预测模型中分别计算对应的累积产气量和累积产水量，并对比计算结果与实际的累积产气量和累积产水量之间的误差，采用迭代法不断优化假设值，直至误差达到合理的精度，最终确定优化后的解吸半径和排水半径为实际值，具体包括以下步骤：(1)厘定煤层气储层动态特征：将上述定义的煤层气井地质参数代入动态模型中，分别刻画煤储层动态孔隙度和动态含水饱和度与储层压力之间的关系，并将动态曲线应用于后续计算流程中；(2)确定模型计算使用的基础数学方法：由于地质参数和生产数据如井底流压和累积气/水产量是已知量，而排水半径和解吸半径是未知量，因此采用迭代算法进行计算，通过假设未知量代入该方法计算累积气/水产量，不断优化假设值直到计算结果与实际生产数据之间的误差小于1％，定义为合理精度；(3)计算单相水流阶段的排水半径：代入实际生产数据，当井底流压大于临界解吸压力时，假定一个排水半径ξi值，代入模型中刻画排水区内压降漏斗动态特征并且计算累积产水量w
p1
，若计算结果w
p1
与实际累积产水量w
preal
之间的误差达到合理精度，则该假设值对应为实际排水半径，否则假设另一个排水半径重新计算；(4)计算气水两相流阶段的排水半径和解吸半径：代入实际生产数据，当井底流压小于临界解吸压力时，首先假设解吸半径ξ
cd
，代入模型中刻画解吸区内气相压降漏斗动态
特征并且计算累积产气量g
p
，通过不断优化假设值直到计算结果g
p
与实际累积产气量g
preal
之间的误差达到合理精度；其次基于解吸半径ξ
cd
和气相压降漏斗计算解吸区内的产水量w
p2
；最后假设排水区内排水半径ξi，持续优化假设值直到计算得到的排水区内产水量和解吸区内产水量之和(w
p1
+w
p2
)与实际累积产水量w
preal
之间的误差达到合理精度；(5)将线性域中计算结果转化为椭圆域中：为了直观地获得椭圆域中压力传播形态特征，分别定义xi和yi、x
cd
和y
cd
为椭圆域中排水区、解吸区的最大半轴长和最小半轴长，遵循：遵循：
23.将完整的生产数据代入计算流程中，绘制生产阶段内解吸半径和排水半径的动态曲线，随着煤层气的不断产出，解吸半径曲线逐渐增加，而对于排水半径，由于生产边界是待解值，因此模型中无法定义拟稳态流压力状态方程，导致计算的排水半径曲线出现先增加后减小的形态，当排水半径曲线与解吸半径曲线相交于一点时，交点对应的范围为煤层气井的生产边界。
24.下面以沁水盆地南部柿庄南区块井间距约250米的2口煤层气井为例，对欠饱和储层煤层气井生产边界进行定量预测。如图3、4所示，井a为一口高产井，日均产气量大于1500m3/d，可以保持高产稳产，其产水和井底流压前期逐渐下降，后期保持低值；而井b的产能特征曲线表明该井受不合理的工作制度影响，井底流压在前期快速下降，导致产气量快速达到峰值后快速下降至1000m3/d以下。通过测井试井数据、查阅文献、实验测试以及数值模拟历史拟合调整，准确获得这两口井的基本地质，其中bw为1，cw为0.00045mpa-1
，ε
max
为0.7％，h为6m，lf为60m，r
wf
为0.1m，t为300k，μw为0.656mpa
·
s，μg为0.01134mpa
·
s，ρ为1.4t/m3，其余地质参数如表1所示。表1.目标井地质参数
25.首先将地质参数代入模型中，定量计算这两口井的动态含水饱和度和动态孔隙度，如图5、6所示。从图中可以看出，当压力小于临界解吸压力时，a井含水饱和度随压力下降而不断降低，下降梯度也逐渐减缓；与a井相比，b井的含水饱和度在低于临界解吸压力时陡降，之后趋于平缓下降；两口井的孔隙度在降压过程中都存在前期下降后期逐渐增加的趋势。
26.通过结合储层静态地质参数和动态特征，代入实际生产数据，利用本专利提出的
计算方法，计算煤层气生产过程中排水半径和解吸半径的变化曲线。从图7、8中可以直观地看出解吸半径和排水半径的传播特征明显不同：随着煤层气的解吸和产出，解吸半径逐渐增加，但是排水半径却呈现出先增加后减小的趋势。值得注意的是，实际生产过程中排水半径不可能出现减小的现象，分析原因主要是由于压力传播至生产边界后地层中流体的渗流状态应遵循拟稳态流，但是该模型是以计算煤层气井的生产边界为目的，因此模型中只考虑了瞬时稳态流而无法考虑拟稳态流。最终当排水半径和解吸半径相交时，对应的范围即为煤层气井的生产边界。从图中可以看出两口井分别在550天和200天左右达到生产边界，排水半径和解吸半径的实际扩展曲线如图9、10所示。为了方便观察分析，利用公式(23,24)将图9、10的计算结果从线性域转化为椭圆域，可以得到图11、12的曲线，其中井a的椭圆长半轴可以达到约120米，近似等于井间距的一半，而井b的椭圆长半轴仅为80米，远小于井间距的一半。综上分析，井a达到的边界为井间压力干扰边界，较远的生产边界和压力干扰使该井在后期可以实现高产稳产；不合理的工作制度导致井b达到的边界为伤害边界，较近的生产边界使该井后期产能受限，只能维持低水平生产。
27.进一步评价动态含水饱和度对压力传播和生产边界预测的影响。从图13中可以看出，动态含水饱和度对气/水相压力传播的影响是明显不同的：在生产初期，由于排水区内含水饱和度等于初始值且不发生变化，因此动态含水饱和度对此区域水相压力状态方程无影响；但在解吸区内若不考虑含水饱和度的动态变化，则意味着压降过程中煤储层孔隙内的含水饱和度会直接从初始值降至束缚水饱和度，高估了孔隙中的可采水量，导致更多的地层水排出，从而在相同累计产水量情况下计算得到更小的排水半径；相比之下，不考虑动态含水饱和度会使含气饱和度偏大，即更多的解吸气残余在孔隙中，最终导致在相同累计产气量情况下计算得到更大的解吸半径。此外，由于解吸区内的地层水产量占累积产水量的比重大，而残余在孔隙中的煤层气体积远小于煤层气产量，因此动态含水饱和度对排水半径扩展的影响远大于对解吸半径的影响。更重要的是，若不考虑含水饱和度的动态变化会导致预测的生产边界范围减小、时间提前，对压降漏斗的定量计算造成巨大误差。因此，考虑动态含水饱和度会使生产边界的计算结果更加精确。
28.本实施例并非对本发明的形状、材料、结构等作任何形式上的限制，凡是依据本发明的技术实质对以上实施例所作的任何简单修改、等同变化与修饰，均属于本发明技术方案的保护范围。