一种基于离散不变性网格卷积算子的流场建模方法

1.本发明属于流体力学技术领域，具体涉及一种流场建模方法。


背景技术：

2.在流体力学领域，流场信息高效准确的获取，对于气动优化、流动控制和不确定性量化等应用至关重要。流场是典型的高维度、多尺度、非线性系统，使得传统机器学习技术在流场建模方面存在局限性。浅层神经网络难以表征复杂系统的动力学行为，同时全连接架构无法提取结构化空间信息，且对计算资源消耗极大。为了降低系统的复杂度，提高计算效率，数据降维方法在流场建模领域得到广泛研究。但是，数据降维方法存在难以应用于多尺度、瞬态和间断过程，以及在发生移动、缩放及旋转变换时无法保证不变性的显著不足。此外，数据降维方法仅能建立全阶状态的降维嵌入，未建立高维数据流形空间与低维表示空间的相互映射，缺乏双向的显示映射函数关系。
3.随着深度学习方法和计算机软/硬件的不断发展，以卷积神经网络(convolutional neural networks,cnns)为代表的深度学习方法，以其局部连接和权重共享的特性，能够提取空间结构信息，具备强大的非线性映射能力，在流场建模领域得到极大关注，展现出广阔的应用前景。但是，由于标准卷积算子仅能处理均匀分布的像素化数据，因此已有工作大都采用将非均匀流场投影到均匀笛卡尔网格的数据预处理方法。像素化处理会造成几何信息缺失，无法表征近壁区流场，甚至在几何内部生成非物理解。此外，cnns依赖于离散化，数据集需要预处理为统一格式，且训练之后的模型在不同分辨率之间难以泛化。在人工智能领域，为了处理非欧式结构数据，图卷积神经网络(graph convolutional networks,gcns)得到了快速发展。但是，gcns对算力和内存都有极高的要求，且多层gcns的过平滑问题导致对复杂系统的表征能力有限，从而限制了gcns在流场建模领域的应用。


技术实现要素：

4.为了克服现有技术的不足，本发明提供了一种基于离散不变性网格卷积算子的流场建模方法，首先构建研究对象的几何样本数据库；再进行网格划分，生成非均匀结构化网格；将网格导入cfd求解器进行流场求解；计算目标节点的一阶邻域节点特征作为图特征，计算表征几何的特征作为节点特征；然后堆叠多层离散不变性网格卷积算子构建深度卷积神经网络；以流场变量作为深度卷积神经网络输出，训练深度卷积神经网络至收敛。本发明能够提取空间结构信息，具有表征能力强、计算成本小和易扩展的特点。
5.本发明解决其技术问题所采用的技术方案包括如下步骤：
6.步骤1：采用cad软件构建研究对象的几何样本数据库；
7.步骤2：采用网格划分软件对研究对象的几何模型进行网格划分，生成非均匀结构化网格；
8.步骤3：将步骤2生成的非均匀结构化网格导入cfd求解器进行流场求解，得到流场变量；
9.步骤4：在非均匀结构化网格节点上根据网格结构计算目标节点的一阶邻域节点特征作为图特征；
10.步骤5：在网格节点上根据几何信息计算表征几何的特征作为节点特征；
11.步骤6：将图特征输入神经网络计算目标节点的权重，并用权重更新目标节点特征；
12.步骤7：将更新之后的目标节点特征通过卷积算子，在邻域内再更新目标节点特征；
13.步骤8：把步骤6和步骤7的两步更新计算称为离散不变性网格卷积算子，堆叠多层离散不变性网格卷积算子构建深度卷积神经网络；
14.步骤9：以流场变量作为深度卷积神经网络输出，训练深度卷积神经网络至收敛；
15.步骤10：将新对象通过步骤2、步骤4和步骤5步骤计算图特征和节点特征，再利用步骤9训练完成的模型即能预测对应的流场信息。
16.进一步的，所述步骤2中生成非均匀结构化网格时，不约束采用统一的网格拓扑结构，可以是满足cfd网格无关性的任意非均匀结构化网格，即不同的几何可以有不同的网格生成参数。
17.进一步的，所述步骤4中目标节点的一阶邻域节点特征包括8个距离ρ
i,i
＝[ρ1,ρ2,
…
,ρ8]
t
和角度θ
i,j
＝[θ1,θ2,
…
,θ8]
t
，对于网格边界不足8个邻域节点的采用补零处理；距离ρ定义为目标节点到邻域节点的欧氏距离，角度θ定义为目标节点指向邻域节点的向量与参考平面的夹角。
[0018]
进一步的，所述步骤5中根据几何信息计算的节点特征具备坐标不变性，不直接以网格节点坐标作为节点特征。
[0019]
进一步的，所述步骤6中的目标节点的权重计算表示为：
[0020][0021]
其中，和分别为用神经网络表示的距离和角度的权重函数；
[0022]
进一步的，所述步骤9中训练深度卷积神经网络的损失函数为：
[0023]
loss＝mse+λ1·
rad+λ2·
layer
[0024][0025][0026]
[0027]
式中，mse表示流场全局损失，负责模型整体精度；grad表示一阶和二阶梯度损失，以弱物理约束的形式负责流场光滑性；layer表示流场第一层网格损失，负责近壁区流场信息；λ1和λ2是权重因子，负责约束三个损失为同一个数量级；h和w表示非均匀结构化网格的周向和法向网格节点数，ny表示输出特征的通道数，y
n,i,j
表示第n个通道索引为(i,j)的真值，表示第n个通道索引为(i,j)的模型预测结果；h表示周向，w表示法向，y
n,i,1
表示几何表面第n个通道索引为i的真值，表示几何表面第n个通道索引为i的模型预测结果。
[0028]
本发明的有益效果如下：
[0029]
本发明提供的基于离散不变性网格卷积算子的流场建模方法，相比传统浅层机器学习和数据降维方法，能够提取空间结构信息，具有表征能力强、计算成本小和易扩展的特点。所提供的建模方法充分利用了卷积神经网络和流场结构化网格的特点，相比标准卷积算子具有离散不变性的优势，极大放松了对数据结构的要求。能够直接在物理平面的邻域内更新节点特征来近似积分算子，准确预测全流场并兼顾近壁区信息，对于指导后续工作开展具有重要意义。
附图说明
[0030]
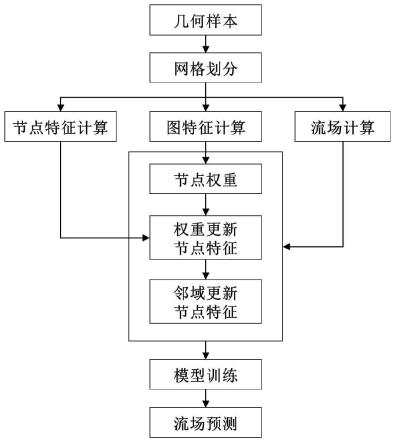
图1为本发明基于离散不变性网格卷积算子的流场建模方法流程图。
[0031]
图2为本发明实施例naca0012翼型非均匀结构化网格图。
[0032]
图3为本发明离散不变性网格卷积算子图。
[0033]
图4为本发明基于离散不变性网格卷积算子的深度卷积神经网络图。
具体实施方式
[0034]
下面结合附图和实施例对本发明进一步说明。
[0035]
本发明的目的是提供一种基于离散不变性网格卷积算子的流场建模方法。采用神经网络根据网格结构计算目标节点的一阶邻域节点权重，并耦合卷积算子在邻域内更新目标节点特征来近似积分算子，建立无限维函数空间的映射。不需要在物理空间对流场采用像素化预处理，能够直接基于非均匀结构化网格进行流场建模，不依赖于计算域离散化格式，能够高效准确地表征全流场并兼顾近壁区信息，用于指导后续工作的开展。
[0036]
一种基于离散不变性网格卷积算子的流场建模方法，主要包括训练样本获取、数据预处理和模型构建与训练部分，包括如下步骤：
[0037]
步骤1：针对所研究的对象，采用cad软件(如catia/rhino)构建几何样本数据库；
[0038]
步骤2：采用网格划分软件(如icem/pointwise等)对研究对象的几何模型进行网格划分，生成非均匀结构化网格；不约束采用统一的网格拓扑结构，可以是满足cfd网格无关性的任意非均匀结构化网格，即不同的几何可以有不同的网格生成参数；
[0039]
步骤3：将步骤2生成的非均匀结构化网格导入cfd求解器进行流场求解，得到流场变量；
[0040]
步骤4：在非均匀结构化网格节点上根据网格结构计算目标节点的一阶邻域节点特征作为图特征；目标节点的一阶邻域节点特征包括8个距离ρ
i,j
＝[ρ1,ρ2,
…
,ρ8]
t
和角度θ
i,j
＝[θ1,θ2,
…
,θ8]
t
，对于网格边界不足8个邻域节点的采用补零处理；距离ρ定义为目标
节点到邻域节点的欧氏距离，角度θ定义为目标节点指向邻域节点的向量与参考平面的夹角；
[0041]
步骤5：在网格节点上根据几何信息计算表征几何的特征作为节点特征；节点特征具备坐标不变性，不直接以网格节点坐标作为节点特征。
[0042]
步骤6：将图特征输入神经网络计算目标节点的权重，并用权重更新目标节点特征；目标节点的权重计算表示为：
[0043][0044]
其中，和分别为用神经网络表示的距离和角度的权重函数；
[0045]
步骤7：将更新之后的目标节点特征通过卷积算子，在邻域内再更新目标节点特征；
[0046]
步骤8：把步骤6和步骤7的两步更新计算称为离散不变性网格卷积算子，堆叠多层离散不变性网格卷积算子构建深度卷积神经网络；
[0047]
步骤9：以流场变量作为深度卷积神经网络输出，训练深度卷积神经网络至收敛；训练深度卷积神经网络的损失函数为：
[0048]
loss＝mse+λ1·
rad+λ2·
layer
[0049][0050][0051][0052]
步骤10：将新对象通过步骤2、步骤4和步骤5步骤计算图特征和节点特征，再利用步骤9训练完成的模型即能预测对应的流场信息。
[0053]
具体实施例：
[0054]
以下通过一个示例详细解释本模型的使用方法，下面的实施例是示例性的，仅用于解释本技术，而不能理解为对本技术的限制。
[0055]
实施例：
[0056]
s1：以naca0012为基准几何，通过添加扰动构建几何样本数据库；
[0057]
s2：采用网格划分软件pointwise对几何模型进行网格划分，生成非均匀结构化网格；采用满足cfd网格无关性的多组网格生成参数，不同几何样本随机选取一组参数生成非均匀结构化网格。
[0058]
s3：将计算网格导入cfd求解器进行流场求解，得到所需流场变量；
[0059]
s4：在网格节点上根据网格结构计算一阶邻域节点特征作为图特征；目标节点的一阶邻域节点特征包括8个距离ρ
i,j
＝[ρ1,ρ2,...,ρ8]
t
和角度θ
i,j
＝[θ1,θ2,...,θ8]
t
，对于网格边界不足8个邻域节点的采用补零处理。以目标节点的右邻域节点记为1，逆时针方向标记其余邻域节点。距离ρ定义为目标节点到邻域节点的欧氏距离，角度θ定义为目标节点指向邻域节点的向量与参考平面的夹角。
[0060]
s5：在网格节点上根据几何信息计算表征几何的特征作为节点特征，并作为模型输入；根据几何信息计算的节点特征包括：网格节点到翼型表面最近的距离；当地点切线方向与翼型0
°
迎角的夹角；当地点曲率；当地点到翼型前缘点的测地距离；当地点到翼型尾缘点的测地距离；网格节点到翼型表面所有离散点的距离的均值。当地点指的是翼型表面上到网格节点距离最近的点。
[0061]
s6：通过神经网络根据图特征计算目标节点的权重，并用权重更新目标节点特征；目标节点的权重的计算表示为：
[0062][0063]
和分别为三层全连接神经网络表示的距离和角度的权重函数，采用指数形式是由于积分算子的距离衰减特性。
[0064]
s7：通过卷积算子根据更新之后的节点特征，在邻域内更新目标节点特征；
[0065]
s8：把s6和s7的两步更新计算称为离散不变性网格卷积算子，堆叠多层该算子构建深度卷积神经网络；
[0066]
s9：以x和y方向的速度分量以及压力作为模型输出，训练深度卷积神经网络至收敛；
[0067]
s10：将新几何通过s2、s4和s5步骤计算图特征和节点特征，利用训练之后的模型即可高效准确的预测对应流场的速度和压力信息。