一种城市雨水井多点位水深快速预报的方法

1.本发明涉及城市洪涝预报领域，尤其涉及一种城市雨水井多点位水深快速预报的方法。


背景技术：

2.快速城市化使得城市下垫面不透水面积迅速增加，不可避免的会对自然生态系统产生一些影响，其中包括：不透水面积增加、水域和绿色植被减少、雨水下渗量降低以及区域内水流的汇流速度加快等。这些改变导致城市区域水文现象发生显著变化，影响到蒸发、径流、下渗等水循环过程的各个环节，引发诸多水文效应，如水循环速率加快、区域蒸发减少、地表径流量增加、流速加快、洪峰提高、峰现时间提前等，上述变化一定程度上使得城市洪涝灾害风险増加。
3.城市洪涝灾害的根本原因是排水系统供需不平衡，即进入排水系统的水量超出了其本身的可容纳量。目前，主要通过两条途径来进行城市排水系统的管理：物理扩容排水系统和建立城市雨水井水深快速预报模型。
4.对于基础设施已成型的城市而言，进一步加强基础设施建设提高排水管网容量不仅需要巨额的资金投入还要大量的人力支持。因此，从城市洪涝预报管理着手，对短时强降雨下的径流进行提前预测，及时采取防护措施，从而有效减少灾害损失，是一项重要的非工程措施。
5.城市洪涝预报管理将地理信息技术、计算机技术等有效地综合应用于洪涝预报领域，它既可为决策机构的领导提供道路积水的实时信息，也可为市政排水管理机构提供调度支持，还可通过大众传媒为广大老百姓提供出行指南，从我国城市洪涝灾害防治的现实需求和智慧城市建设的发展需求来看，城市洪涝快速预报的研究重要且迫切。
6.基于物理的城市洪涝数值模型已在城市洪涝预测领域取得较大成功，但存在的缺点是需要相当长的模拟时间，故很难保证提前预测。而神经网络模型不考虑底层物理关系，关注于自变量与因变量的非线性相关关系，使其在计算速度上较物理模型有很大的优势。目前，已有许多城市洪涝预测神经网络模型，但多集中于单点位预报模型的研究，缺乏对雨水井多点位之间空间相关性的考虑，割裂了点位间相关性与模型拓扑结构的联系，因而极易出现模型变量选择不当，各层之间传递函数、隐藏神经元数量、训练迭代历元及其他相关参数陷入局部最优解的问题。


技术实现要素：

7.为了解决以上问题，本技术提供的一种城市雨水井多点位水深快速预报的方法，首先构建城市街道-雨水下水道双排水系统耦合模型对城市中未布置水位计的雨水井进行水深数据补充；然后采用基于互相关分析的皮尔逊相关系数法对降雨-水深的时间相关性进行分析，降低了预报的时间成本，同时考虑了预报精度的问题，对雨水井各点位间的空间相关性进行分析，本发明不仅提高了雨水井水深的预报速度，还提高了其预报精度。
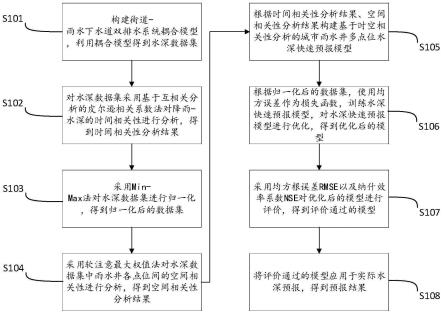
8.本发明方法具体包括以下步骤：
9.s101：构建街道-雨水下水道双排水系统耦合模型，利用耦合模型得到水深数据集；
10.s102：对水深数据集采用基于互相关分析的皮尔逊相关系数法对降雨
‑ꢀ
水深的时间相关性进行分析，得到时间相关性分析结果；
11.s103：采用min-max法对水深数据集进行归一化，得到归一化后的数据集；
12.s104：采用软注意最大权值法对水深数据集中雨水井各点位间的空间相关性进行分析，得到空间相关性分析结果；
13.s105：根据a、b构建基于时空相关性分析的城市雨水井多点位水深快速预报模型；
14.s106：根据归一化后的数据集，使用均方误差作为损失函数，训练水深快速预报模型，对水深快速预报模型进行优化，得到优化后的模型；
15.s107：采用均方根误差(rmse)以及纳什效率系数(nse)对优化后的模型进行评价，得到评价通过的模型；
16.s108：将评价通过的模型应用于实际水深预报，得到预报结果。
17.进一步地，所述街道-雨水下水道双排水系统耦合模型采用于雨洪管理模型swmm建立。
18.进一步地，步骤s102中时间相关性分析的具体公式如下：
[0019][0020][0021]
式(1)、(2)中，是滑动窗口为i时，n个雨水井的降雨-水深相关系数均值；i是滑动窗口数；pcci(r，dj)是滑动窗口为i时，第j个雨水井的相关系数值；n是雨水井个数；r
t-i
是降雨数据序列中的第t-i个降雨数据；是平均降雨；是雨水井水深数据序列中第j个雨水井的第i+1个水深值；是雨水井水深数据序列中第j个雨水井的水深均值；t是降雨数据序列总长度；sr是降雨数据序列的标准差；是第j个雨水井数据序列的标准差。
[0022]
进一步地，步骤s103中的归一化，具体如下式：
[0023][0024]
式(3)中，x
i*
是归一化后的数据序列；xi是原始数据序列；x
min
是数据序列中的最小值；x
max
是数据序列中的最大值。
[0025]
进一步地，步骤s104中空间相关性分析，具体如下：
[0026][0027][0028][0029][0030]
式(4)-(7)中，αi是第i个雨水井的空间权重系数；是雨水井水深数据序列中第i个雨水井的第j个水深值；t是降雨数据序列总长度； ratio
pcc》n
是皮尔逊相关系数大于n时的比值；a
n＜pcc＜1.0
是各雨水井互相关混淆矩阵中皮尔逊相关系数在n～1.0时的面积；a
total
是各雨水井互相关混淆矩阵总面积；是第i个雨水井皮尔逊相关系数大于n的个数；0＜n＜1。
[0031]
进一步地，步骤s105中，水深快速预报模型具体如下：
[0032][0033][0034][0035]
式(8)-(10)中，是考虑了时空相关性的预测水深；是考虑了时间相关性的预测水深；是输出层中第k个神经元；f(
·
)是激活函数；
⊙
是哈达玛积，矩阵的一类运算；α是雨水井的空间权重系数；是多雨水井水深快速预报模型结构第二层中，隐藏层第q个神经元与输出层第k个雨水井间的权重系数；hq是隐藏层中第q个神经元；m是隐藏层神经元总个数；n是雨水井总个数；是多雨水井水深快速预报模型结构第一层中，输入层第 j个降雨与隐藏层第q个神经元间的权重系数；r
′j是考虑了时间相关性的降雨输入第j个数据；l是最佳滑动窗口长度；其中，ω通过反向传播的方式不断更新，直到模型精度满足要求为止，ω的更新公式为采用为止，ω的更新公式为采用ω
*
为更新后的权重；ω为更新前的权重；η是迭代步长，用于调整收敛速度与精度；e
total
是模型损失函数，用于评判模型精度。
[0036]
进一步地，步骤s106中优化模型的具体过程为：先用公式(11)对数据进行逆归一化处理，再采用公式(12)计算损失函数；
[0037]
x＝x
norm
*(x
max-x
min
)+x
min
ꢀꢀꢀ
(11)
[0038][0039]
式(11)-(12)中，e
total
是预报模型损失函数；是第j个雨水井的预报水深值；dj是第j个雨水井的目标水深值；n是研究区域中雨水井总个数；x是逆归一化后的值；x
norm
是归
一化后的值；x
max
是原始数据序列中的最大值；x
min
是原始数据序列中的最小值；计算出预报模型损失函数值之后，根据不等式e
total
＜e或者e
poch
》m，判别是否进行循环，重新更新权重；若损失函数小于e或者e
poch
大于m，则停止循环，完成模型训练优化。
[0040]
与现有技术相比，本发明的有益效果包括：提高了雨水井多点位水深预报的速度和精度。
附图说明
[0041]
图1是本发明方法流程示意图；
[0042]
图2是城市雨水井多点位水深快速预报模型训练数据；
[0043]
图3是降雨-水深的时间相关性分析图；
[0044]
图4是雨水井间的空间相关性分析图；
[0045]
图5是基于时空相关性分析的城市雨水井多点位水深快速预报模型在某雨水井中的预测结果图；
[0046]
图6是区域内358个雨水井的预报结果评价图；
[0047]
图7是城市雨水井多点位水深快速预报模型训练的框架图。
具体实施方式
[0048]
为了使本发明的目的、技术方案及优点更加清楚明白，以下结合附图及实施例，对本发明进行进一步详细说明。应当理解，此处所描述的具体实施例仅仅用以解释本发明，并不用于限定本发明。
[0049]
请参考图1，本发明提供一种城市雨水井多点位水深快速预报的方法，包括以下步骤：
[0050]
s101：构建街道-雨水下水道双排水系统耦合模型，利用耦合模型得到水深数据集；
[0051]
需要说明的是，耦合模型对城市中未布置水位计的雨水井进行水深数据补充，获取训练数据集；
[0052]
作为一种实施例，本发明中的城市街道-雨水下水道双排水系统耦合模型通过雨洪管理模型(storm water management model，swmm)构建，建立过程可概述如下。
[0053]
双排水系统分为雨水下水道系统与地表街道漫地流系统两个部分。
[0054]
雨水下水道管线系统的排水情况由swmm模型中的输水干线 (extran)模块模拟，此模块采用管道-节点(link-node)的概念，即在管道(link)中满足动量方程，在节点(node)处满足连续性方程，利用一维圣维南方程组(de saint-venant system of equations)计算雨水下水道管线中各断面位置的水力信息和各溢流节点的溢流量。
[0055]
地表街道漫地流系统由swmm模型中的地表径流(runoff)模块模拟，此模块把城市看作一个中小型流域，将其划分为多个子流域即子集水区，降雨在每个子集水面积中产生的地表径流通过非线性水库模型模拟。
[0056]
swmm假设降雨落到地面形成的漫地流直接通过最近的雨水井流入雨水下水道系统，runoff模块产生的径流历线将传至extran模块进行计算。
[0057]
extran模块所需要的输入参数有雨水下水道管渠连接关系、断面形状、长度、曼宁
糙度系数、上下游偏移量、雨水井底高程和最大深度以及下游边界条件等水力参数；runoff模块所需要的输入参数有次集水区面积、特征宽度、地表糙度、平均坡度及不透水区域百分比等水文参数。其中，管道的埋没深度＝雨水井深度-出口偏移量-管道高度，管道的坡度＝[(上游雨水井底高程+进口偏移)-(下游雨水井底高程+出口偏移)]/长度。
[0058]
通过实测数据的验证，所构建街道-雨水下水道双排水系统耦合模型可用于对城市中未布置水位计的雨水井进行水深数据补充。
[0059]
s102：对水深数据集采用基于互相关分析的皮尔逊相关系数法对降雨
‑ꢀ
水深的时间相关性进行分析，得到时间相关性分析结果；
[0060]
需要说明的是，为了降低模型预报的时间成本，在双排水系统耦合模型的数据基础上，采用基于互相关分析的皮尔逊相关系数法对降雨-水深的时间相关性进行分析；步骤s102中时间相关性分析的具体公式如下：
[0061][0062][0063]
式(1)、(2)中，是滑动窗口为i时，n个雨水井的降雨-水深相关系数均值；i是滑动窗口数；pcci(r，dj)是滑动窗口为i时，第j个雨水井的相关系数值；n是雨水井个数；r
t-i
是降雨数据序列中的第t-i个降雨数据；是平均降雨；是雨水井水深数据序列中第j个雨水井的第i+1 个水深值；是雨水井水深数据序列中第j个雨水井的水深均值；t是降雨数据序列总长度；sr是降雨数据序列的标准差；是第j个雨水井数据序列的标准差。
[0064]
s103：采用min-max法对水深数据集进行归一化，得到归一化后的数据集；
[0065]
需要说明的是，用min-max法对数据集进行归一化处理，避免因数值梯度爆炸而导致模型无法训练的问题。步骤s103中的归一化，具体如下式：
[0066][0067]
式(3)中，x
i*
是归一化后的数据序列；xi是原始数据序列；x
min
是数据序列中的最小值；x
max
是数据序列中的最大值。
[0068]
s104：采用软注意最大权值法对水深数据集中雨水井各点位间的空间相关性进行分析，得到空间相关性分析结果；
[0069]
需要说明的是，为了提高模型预报精度，采用软注意最大权值法对水深数据集中雨水井各点位间的空间相关性进行分析；首先采用公式(4)对研究区域内各雨水井间的空间相关性进行分析，分析结果如图4所示。从图 4(a)中可见，本发明案例内的绝大多数雨水井的空间相关系数在0.6～1.0。此外，从图4(b)中可以直观地看出，各雨水井间的空间相关
系数大于0.8、 0.6、0.4的面积占比分别是0.742、0.894、0.939。这表明超过74％的雨水井具有很强的互相关性(空间相关系数＝0.8-1.0)，接近90％的雨水井具有强互相关性(空间相关系数＝0.6-1.0)，超过93％的雨水井具有较强的互相关性(空间相关系数＝0.4-1.0)。因此，本发明案例中雨水井均具有较强的互相关性，可将所有雨水井作为一个整体进行多输出拓扑结构的构建。
[0070][0071][0072][0073][0074]
式(4)-(7)中，αi是第i个雨水井的空间权重系数；是雨水井水深数据序列中第i个雨水井的第j个水深值；t是降雨数据序列总长度； ratio
pcc》n
是皮尔逊相关系数大于n时的比值；a
n＜pcc《1.0
是各雨水井互相关混淆矩阵中皮尔逊相关系数在n～1.0时的面积；a
total
是各雨水井互相关混淆矩阵总面积；是第i个雨水井皮尔逊相关系数大于n的个数；0＜n＜1。
[0075]
s105：根据a、b构建基于时空相关性分析的城市雨水井多点位水深快速预报模型；
[0076]
步骤s105中，水深快速预报模型具体如下：
[0077][0078][0079][0080]
式(8)-(10)中，是考虑了时空相关性的预测水深；是考虑了时间相关性的预测水深；是输出层中第k个神经元；f(
·
)是激活函数；
⊙
是哈达玛积，矩阵的一类运算；α是雨水井的空间权重系数；是多雨水井水深快速预报模型结构第二层中，隐藏层第q个神经元与输出层第k个雨水井间的权重系数；hq是隐藏层中第q个神经元；m是隐藏层神经元总个数；n是雨水井总个数；是多雨水井水深快速预报模型结构第一层中，输入层第 j个降雨与隐藏层第q个神经元间的权重系数；r
′j是考虑了时间相关性的降雨输入第j个数据；l是最佳滑动窗口长度；其中，ω通过反向传播的方式不断更新，直到模型精度满足要求为止，ω的更新公式为采用为止，ω的更新公式为采用ω
*
为更新后的权重；ω为更新前的权重；η是迭代步长，用于调整收敛速度与精度；e
total
是模型损失函数，用于评判模型精度。
[0081]
s106：根据归一化后的数据集，使用均方误差作为损失函数，训练水深快速预报模型，对水深快速预报模型进行优化，得到优化后的模型；
[0082]
需要说明的是，由于训练模型时已经对数据进行归一化处理，在计算损失函数之前，需要先用公式(11)对数据进行逆归一化处理，再采用公式 (12)计算损失函数。
[0083]
x＝x
norm
*(x
max-x
min
)+x
min
ꢀꢀꢀꢀ
(11)
[0084][0085]
式(11)-(12)中，e
total
是预报模型损失函数；是第j个雨水井的预报水深值；dj是第j个雨水井的目标水深值；n是研究区域中雨水井总个数；x是逆归一化后的值；x
norm
是归一化后的值；x
max
是原始数据序列中的最大值；x
min
是原始数据序列中的最小值；计算出预报模型损失函数值之后，根据不等式e
total
＜e或者e
poch
＞m，判别是否进行循环，重新更新权重；若损失函数小于e或者e
poch
大于m，则停止循环，完成模型训练优化。
[0086]
s107：采用均方根误差(rmse)以及纳什效率系数(nse)对优化后的模型进行评价，得到评价通过的模型；
[0087]
步骤s107中，模型的评价指标如下：
[0088][0089][0090]
式(13)-(14)中，m是雨水井总个数；是雨水井多点位水深快速预报模型的预报水深值；di是目标水深值；是目标水深平均值。
[0091]
s108：将评价通过的模型应用于实际水深预报，得到预报结果。
[0092]
下面通过一个实例验证本发明方法的有益效果，具体如下：
[0093]
本发明实例采用的数据为某城市区域358个雨水井的24场降雨-水深混合数据集，混合数据集包括水位计实测数据以及街道-雨水下水道双排水系统耦合模型对无水位计位置的补充数据，区域内某点数据过程线见图2，其时间分辨率为10min。将混合数据集划分为训练集和测试集。训练集包括 20场降雨-水深数据，其中80％为训练数据，20％为验证数据，此外，测试集包括4场降雨-水深数据。
[0094]
基于时空相关性分析的雨水井多点位水深快速预报过程如下：
[0095]
1)预报模型输入输出拓扑结构的确定：为了确定预报模型的输入、输出拓扑结构，分别对降雨-水深的时间相关性以及雨水井各点位间的空间相关性进行分析。首先，考虑了影响不同雨水井点位水深的有效降雨跨度，即考虑了降雨-水深的时滞性，通过对降雨-水深的时间相关性分析(见图 3)，确定预报模型的输入拓扑结构。本发明实例所研究区域内的358个雨水井点位在不同降雨-水深时间差下的相关性分析结果如图3(a)所示，每根折线代表一个雨水井点位。从图中可以看出，到300分钟时所有雨水井的时间相关性系数都小于0.4，说明降雨-水深的时间相关性超过特定时间段后呈现弱相关。因此，确定有效的降雨输入值就是确定降雨-水深时间相关性由强转弱的时间点。由于时间相关性强的降雨对水深影响较大，故计算不同时间差下时间相关性系数大于0.4和大于0.6的雨水井点位占比。从
图3(b) 中可以看出，当时间相关性系数大于0.6时，雨水井点位比例在8*10min 时大幅下降小于50％，在13*10min时趋于零；当时间相关性系数大于0.4 时，在19*10min时雨水井比例大幅下降小于50％，在28*10min时趋于零。因此，我们猜测降雨时间序列较好的输入维度在13～28。得到降雨-水深时间相关性分析结果之后，采用试算法进一步确定预报模型的输入拓扑结构 (图3(c))。本发明案例中采用lstm(long short-term memory network) 运算网络来说明本发明的可行性。为了消除随机误差的影响，本发明实例采用4场台风降雨数据进一步确定模型的输入拓扑结构，从图3(c)中可以看出，随着滑动窗口的增加，4个模拟结果的纳什效率系数都不断上升。并且在滑动窗口为15之后达到平稳，则雨水井多点位水深快速预报模型的最佳输入拓扑确定为15。
[0096]
其次，考虑了不同雨水井点位间水深变化的差异性，以及不同雨水井点位间水深的相互影响。采用软注意最大权值法对雨水井各点位间的空间关联性进行分析(见图4)，以确定预报模型的输出拓扑结构，本发明实例所研究区域内的绝大多数雨水井各点位间的空间相关性系数在0.6～1.0。此外，研究区域雨水井各点位间的空间关联性强弱区间占比可以在图4(a)中更直观看出，通过公式(4)可得到空间相关性系数大于0.8、0.6、0.4的面积占比分别是0.742、0.894、0.939。这表明研究区域超过74％的雨水井具有很强的互相关性(空间相关性系数＝0.8-1.0)，接近90％的雨水井具有强互相关性(空间相关性系数＝0.6-1.0)，超过93％的雨水井具有较强的互相关性(空间相关性系数＝0.4-1.0)。因此，研究区域中雨水井均具有较强的互相关性，可将所有雨水井作为一个整体进行多输出拓扑结构的构建。
[0097]
2)模型构建：根据降雨-水深的时间相关性以及雨水井各点位间的空间相关性，构建雨水井多点位水深快速预报模型，模型的公式前文已经交代，这里不再具体阐述；这里请参考图7，图7是城市雨水井多点位水深快速预报模型训练的框架图。
[0098]
本发明案例中采用adam优化算法，η取0.01；ω
*
为更新后的权重；r
′j是考虑了时间相关性的降雨输入第j个数据；l是最佳滑动窗口长度；是多雨水井水深快速预报模型结构第一层中，输入层第j个降雨与隐藏层第 q个神经元间的权重系数；f(
·
)代表输出层的激活函数，本发明中采用 sigmoid函数；hq是隐藏层中第q个神经元；m是隐藏层神经元总个数；是多雨水井水深快速预报模型结构第二层中，隐藏层第q个神经元与输出层第k个雨水井间的权重系数；是考虑了时间相关性的第k个雨水井水深值；
⊙
是哈达玛积，矩阵的一类运算；α是雨水井的空间权重系数。
[0099]
为了保证模型精度，可首先对数据集进行训练数据集和测试数据集的划分并进行归一化处理，各数据集特征值见表1，可以看出训练集的数据特性涵盖了测试集。
[0100]
表1 数据集特征表
[0101][0102]
其次，在确定了雨水井多点位水深预报模型的拓扑结构以及数据集的基础上，开始对模型进行训练，训练流程如图1所示。
[0103]
3)模型验证：该案例中采用4场混合数据集对预报结果进行验证，验证结果见图5，预报模型评价指标如图6所示，由于雨水井数量过多，故采用箱型图以及频率分布直方图的方式对模型进行评价，可以看出，基于时空相关性分析的雨水井多点位水深预报模型的rmse和nse中位数分别分布在0.02～0.03之间以及0.975～0.985之间，rmse和nse的均值分别分布在0.02～0.03之间以及0.9～1.0之间，大多数雨水井的rmse低于0.05并且 nse高于0.9，这意味着大多数雨水井的水深预报误差小于0.05m，雨水井多点位水深快速预报模型的预报精度高。
[0104]
综合来看，本发明基于对输出之间相关性的考虑，耦合不同输出之间的相互作用，构建基于时空相关性分析的城市雨水井多点位水深快速预报模型，见图1。
[0105]
采用街道-雨水下水道双排水耦合系统代替传统的雨水下水道排水系统构建水动力模型，同时考虑了雨水下水道系统与街道系统的降雨径流耦合过程，通过雨水井在两个系统之间进行水流交换。
[0106]
考虑了降雨-径流过程中的时滞性对雨水井水深的影响，采用基于互相关分析的皮尔逊相关系数法对降雨-水深的时间相关性进行分析，见图3。
[0107]
考虑了雨水井间的空间相关性对雨水井水深的影响，采用软注意最大权值法对雨水井间的空间相关性进行分析，见图4。
[0108]
本发明的有益效果是：提高了雨水井多点位水深预报的速度和精度。
[0109]
以上所述本发明的具体实施方式，并不构成对本发明保护范围的限定。任何根据本发明的技术构思所做出的各种其他相应的改变与变形，均应包含在本发明权利要求的保护范围内。