一种基于视觉的四足仿生机器人模拟动物步态的方法

1.本发明涉及一种基于计算机视觉的四足仿生机器人模拟动物运动状态方法，具体涉及基于dpnet网络的运动参数提取方法，基于运动参数的机器人模拟动物步态方法，属于计算机视觉与图像处理领域。


背景技术：

2.在大型农场养犬类或牧场放牧时为了能够及时发现动物的健康隐患，通常有员工负责定期查看动物的活动情况，但人工观察具有主观性且实时度不高，并且具有人力消耗过大和效率较低的缺点，故精确识别动物的步态状况对于农场和牧场养殖上有较高的应用价值。目前动物行为识别研究较为成熟，但对于动物具体步态的分析还存在以下问题：自然环境中不同光照、场景变换与拍摄不同角度造成的干扰，研究对象本身四肢皮毛的相似性与多目标遮挡带来的关键点定位误差。因此本发明采用深度学习方法利用网络进行自动检测，通过计算机视觉的方式减少了人力物力，同时提高了效率。四足仿生机器人是近年来的热门研究方向，基于其姿态形式多样、适用范围大的特点被广泛应用，相比于步态受限的履带式机器人与体积笨重的轮式机器人，自由度高的四足机器人具有更强的可控性与灵活度，同时对于仿生机器人的性能来说，足式机器人具有轻重量、结构性强的优势，具有更广的应用空间。


技术实现要素：

3.本发明提供了一种基于计算机视觉的四足仿生机器人模拟动物运动状态的方法，旨在应用于四足机器人参与排雷爆破、运载重物等人力难以完成的情况。本发明首先改进了hrnet(high resolution net)网络；其次利用模型生成的运动参数，将四足动物的生理信息结构运用到四足仿生机器人中，构建了全肘式的机器人结构。然后通过d-h参数方法进行正运动学建模，使用拉格朗日方程法对机器人的动能与势能进行计算，解得拉格朗日方程以获取机器人每个关节的力矩，再对机器人前进的理想状态下足端轨迹进行规划，最后通过matlab搭建四足仿生机器人的仿真模型，基于simulink模块分析了机器人质心到原点距离的变化和前进过程中机器人速度与加速度的变化。
4.本发明的技术方案如下：一种基于计算机视觉的四足仿生机器人模拟动物运动状态方法，所述方法具体步骤如下：
5.步骤(1)实验数据采集：拍摄四足动物在道路上的对角小跑运动视频：拍摄视频中图片分辨率为1270
×
720，拍摄设备与四足动物持平且距离四足动物 5-8m，拍摄角度在
±
270
°
之间，在早上8：00-12：00，下午13：00-18：00之间共拍摄十段1min的视频；
6.步骤(2)建立模型结构：在hrnet高分辨率基础网络上进行改进，建立骨架模型；
7.步骤(3)提取动物运动参数：通过步骤(2)建立的模型预测步骤(1)拍摄的视频中四足动物关键点的位置，实现对四足动物运动参数的提取；
8.步骤(4)建立四足机器人模型：将四足动物实体结构信息运用到机器人整体结构
设计中，并结合步骤(3)提取的四足动物的运动参数进行机器人的正运动学建模与动力学分析；
9.步骤(5)机器人对角小跑步态仿真：对机器人的足端轨迹进行了规划，将规划的理想状态下的轨迹同四足仿生机器人的实际运动轨迹进行对比，得出机器人模型可靠，最后通过matlab对机器人模型进行动物运动状态的模拟。
10.步骤(1)中采用摄影机拍摄视频。
11.所述步骤(2)中，模型建立的具体步骤如下：
12.在hrnet高分辨率基础网络输出的最后四个分支后面添加两条路径，第一条路径设置为三层混合空洞卷积，第二条路径设置为含有通道和空间两种注意力机制的模块；
13.其中第一条路径具体为：第一条路径设置为三层混合空洞卷积，基于第一分支与第二分支通道数较少且上下文全局信息较多的表现，选择在前两个输出分支后面添加hdc层，假设空洞卷积率为d，网络中原始卷机核尺寸为k
×
k，那么空洞卷积核大小n为
14.n＝k+(k-1)
×
(d-1)
ꢀꢀꢀꢀꢀꢀ
(1)
15.由于空洞卷积在扩大特征信息感受野的同时会出现特征像素读取失去连续性的现象，参与卷积运算的像素点均为膨胀后卷积核的有效权重位置，这样会引起栅格效应，丢失部分有价值的特征信息从而影响到最终网络分类预测的准确性，故采用不同膨胀系数的空洞卷积并将三层卷积操作结合为一条路径，其中为了最大限度地填充丢失部分的像素点从而确保信息表征的全面性，需满足在当前层的最大膨胀系数不大于网络原始卷积核尺寸，即满足条件
16.mi≤k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
17.mi＝max[m
i+1-2di,m
i+1-2(m
i+1-di),di]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0018]
式(3)中mi为第i层的最大膨胀系数，di为第i层的空洞卷积率，max为取三层中的最大值，令中间层m2≤3，可得到各层的空洞卷积率d1＝1，d2＝2，d3＝5，由此可改进前两个分支中普通常规卷积带来的特征表征能力较弱与信息全局性较差两方面；
[0019]
第二条路径具体为：设置为含有通道和空间两种注意力机制的模块，具体为在第三分支与第四分支的输出后面添加并行注意力模块pam，基于后两分支通道数较多故所携带的图像细节信息较全面的特点，将通道注意力机制与空间注意力机制相融合，从而为不同通道的表征和像素的位置分配相应的权重，使得与分类有关的像素点信息在网络训练中更加突出后两分支的输出特征经过最大池化、平均池化与中值池化的操作后将得到的特征向量进行通道和空间的权值计算；先采用1
×
1的卷积调整通道数为256并进行数据批标准化，在两种注意力机制组合输出的特征向量后降低维度，最后通过sigmoid激活获取并分配2个分支0-1的权重值，生成的通道与空间注意力图计算如下：
[0020]
out
channel
＝w(mlp*(in
avgpool
+in
maxpool
+in
medpool
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0021]
out
spatial
＝w(f*(in
avgpool
,in
maxpool
,in
medpool
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0022][0023]
上式中out
channel
为通道注意图，out
spatial
为空间注意力图，w为sigmoid激活函数，mlp为多层感知机(multilayer perception)用以共享权值，f为3
×
3的卷积操作，in表示后两分支的输出特征，out
branch
为通道权重和空间权重分别与输出特征对位相乘再相加得到的最终分支特征；
[0024]
两条路径经过特征融合将低级特征弥补上语义信息同时把高级特征增添上空间信息；
[0025]
通过以上对hrnet高分辨率基础网络的改进，先获得了四足动物的关节点位置再逐次连接形成了骨架模型。
[0026]
所述步骤(3)中，运动特征参数提取的具体步骤如下：
[0027]
①
同侧步距参数：
[0028]
在模型中获取研究对象一个步态周期内四个角点的坐标位置后，通过定位每一肢踝关节离图像原点距离最远和最近时的两关节坐标欧氏距离变化，计算四肢踝关节相对本身迈步距离的平均值，假设分别为第fi帧和第f
i+1
帧图像中动物左前肢踝关节坐标，则为动物右前肢踝关节坐标，为动物左后肢踝关节坐标，为动物右后肢踝关节坐标，步距计算式为
[0029][0030]
式中为图片像素与实际距离的转换系数，本研究将动物四肢在一个周期内前进的距离求和并取平均值得到步距；
[0031]
②
关节角度参数：
[0032]
选取标注的关键点3即左前肢膝关节点，将三种研究对象在连续运动周期内膝关节的变化做对比分析，假设模型最终识别的动物髋关节坐标为(xa,ya)，膝关节坐标为(xb,yb)，踝关节坐标为(xc,yc)，则基于关节两点之间的坐标变化，通过坐标向量的平方差可求得a，b，c三个距离，关节计算式为
[0033][0034][0035][0036][0037]
通过式(8)-式(11)计算得到动物的关节角度变化参数。
[0038]
所述步骤(4)中，机器人模型建立的具体步骤如下：
[0039]
①
机器人机体结构设计：
[0040]
通过对四足动物身骨骼与肌肉纹理的分析，并结合四足动物在奔跑运动中的特性，使用全肘式机械结构作为仿生机器人的机体结构，在连接第一段与第二段的髋关节处设置一个自由度，在连接第二段与第三段的膝关节处设置一个自由度，则基于仿生犬机器人的四肢共有八个自由度；
[0041]
②
机器人运动学建模
[0042]
机器人包含世界坐标系{w}，机体坐标系{b}，腿部坐标系{l}；其中腿部坐标系又包含髋关节坐标系{1}和膝关节坐标系{2}以及足端坐标系{3}，通过d-h 参数计算机器人设置的坐标系中相邻两个系的坐标变换矩阵，经过相邻两个坐标系的平面平移和空间旋转
过程后，总体变换矩阵公式为
[0043][0044]
其中，表示第n个坐标系和第n+1个坐标系之间的坐标变换矩阵，rot ()和trans表示经过经过了x轴与z轴的旋转和平移操作，xi表示x轴，αi表示在坐标系空间中的旋转角度，θi为关节坐标系旋转的角度，ai表示两关节点之间的连杆长度，di表示第i个坐标系与第i+1个坐标系之间的偏移距离；
[0045]
将d-h参数带入到式(10)得到
[0046][0047]
其中坐标系相对于z轴进行旋转变换的旋转矩阵为
[0048][0049]
坐标系相对于x轴进行平移变换的平移矩阵为
[0050][0051]
由式(12)与式(13)可得四足仿生机器人的足端坐标系{3}相对于机体坐标系{b}的坐标变换矩阵如下
[0052][0053]
由于t坐标变换矩阵可简写为以下公式
[0054][0055]
上式中为旋转矩阵，为平移矩阵，由上文发明可知机器人设定的髋关节与膝关节之间的连杆长为20cm，膝关节与踝关节之间的连杆长为18cm，则由式(15)得到四足仿生犬机器人的正运动学建模公式为
[0056][0057]
机器人设定的髋关节与膝关节之间的连杆长为l1，膝关节与踝关节之间的连杆长为l2；
[0058]
③
机器人动力学分析
[0059]
假设连杆1和连杆2的质量分别为m1和m2，由此能够得到连杆1和连杆2 的转动惯量如下
[0060][0061][0062]
然后分别取连杆的中心点作为质心，确定连杆1和连杆2的质心位置后对x 与y方向上计算质心坐标，公式为
[0063][0064][0065]r2x
＝l
1 cos(θ1(t))+(l2cos((θ1(t)+θ2(t)))/2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(23)
[0066]r2y
＝l
1 sin(θ1(t))+(l2sin((θ1(t)+θ2(t)))/2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(24)
[0067]
两个连杆的速度结果为
[0068][0069][0070]
表示第一根连杆的角速度，表示第二根连杆的角速度；
[0071]
机器人总动能e为连杆1和连杆2的动能之和，公式结果为
[0072][0073]
c2表示cosθ2；
[0074]
机器人总势能为两连杆的势能之和，计算结果为
[0075][0076]
s1表示sinθ1,s
12
表示sinθ1θ2；
[0077]
由拉格朗日方程可知，拉格朗日函数等于机器人动能与势能的差
[0078][0079]
基于拉格朗日函数l分别对θ1,θ2,求偏导，将机器人角加速度与机器人关节力矩τ1,τ2的关系通过矩阵表示出来，则更加直观的看到关系矩阵的变化为
[0080][0081]
④
机器人足端轨迹规划
[0082]
采用复合摆线与贝塞尔曲线的方法，将一个运动周期内机器人足端起始点与落地点之间的曲线进行规划。复合摆线的计算公式为
[0083][0084][0085][0086]
式(31)为四足仿生机器人的摆动相在x与z方向的轨迹，式(32)为四足仿生机器人的支撑相在x与z方向的轨迹，其中xf与xs分别为机器人在x 轴方向的落足点与起步点，zs为机器人在z轴的起步点，式(33)中tf为机器人处于支撑相的时间，t表示一个运动周期，
[0087]
贝塞尔曲线是由很多控制点通过递归的形式逐渐生成的，贝塞尔曲线与复合摆线相比具有更好的速度与加速度连续性，故采用三阶的贝塞尔曲线进行机器人路径规划，公式为
[0088]
b(t)＝p0(1-t)3+3p1t(1-t)2+3p2t2(1-t)+p3t3,t∈[0,1]
ꢀꢀꢀꢀꢀ
(32)
[0089]
式(34)中p0，p1，p2，p3为曲线的四个控制点，通过调节控制点以获取更优的足端轨迹，设置四个控制点分别为机器人起步点(-0.11,-0.36)，最高点 (0,-0.27)，次高点(0.05,-0.28)，落地点(0.11,-0.36)。
[0090]
步骤(5)中采用matlab r2021a的simulink功能对机器人模型进行动物运动状态的模拟。对角小跑步态仿真的具体步骤如下：
[0091]
①
本发明在matlab r2021a的软件环境下进行实验，操作系统是win10 系统，通过simulink功能建立以.slx为后缀的机器人仿真模型，基于simulink
ꢀꢀ
library browser工具库中的模块建立四足仿生机器人的整体结构与运动关系。通过multibody-frames and transforms-world frame建立世界基准坐标系，在其基础上使用工具库中的commonly used blocks为仿真模型添加滤波器或数据形式转换等基础模块，并通过simulink-sinks-scope为机器人的输出端口添加示波器，通过上述建模过程获取机器人的仿真结果；
[0092]
②
本节再对机器人的自身位移与速度等行进参数进行分析。在simulink模型中添
加偏导模块，连接到机器人zyz三个坐标轴方向的输出端，同时偏导模块另一端接上示波器，得到四足仿生机器人在行进过程中的速度与加速度变化曲线图。
[0093]
本发明的工作原理是：
[0094]
(1)hrnet高分辨率基础网络：
[0095]
基于提取运动目标特征参数需要精准定位关节点的特点，本发明选择自下而上的方法，即先获得四足动物的关节点位置再逐次连接形成骨架模型。其中为了解决网络层数加深伴随下采样后分辨率大幅降低的缺点，本发明以hrnet作为基础网络，将原始图片预处理为256
×
256统一大小输入网络，该网络中包含4个模块，每个模块的残差单元从1往上依次增加一个，其中模块3和模块4分别在网络中重复4次和3次。
[0096]
(2)dpnet双路径网络
[0097]
基于hrnet在保持高分辨率的情况下使用常规卷积核3
×
3操作提取特征这一设计，重复大量的相同尺寸卷积操作会减弱图片像素点之间的空间关联性。针对hrnet模型获取的感受野片面并有固定性的情况，本发明在hrnet基础上进行改进，考虑到网络中各层低分辨率逐次交替融合为最终高分辨率的完整性与连贯性，本发明选择在hrnet输出的最后四个分支后面添加两条路径，第一条路径设置为三层混合空洞卷积，第二条路径设置为含有通道和空间两种注意力机制的模块。
[0098]
本发明的有益效果是：
[0099]
(1)本发明通过计算机视觉的方式智能获取动物运动图像并及时分析监测动物的健康情况，能够确保动物日常健康信息的及时获取，防止疾病隐患。
[0100]
(2)本发明在无接触目标对象的情况下提取动物的运动参数，降低了采集数据的难度和不确定性，提高了工作效率。
[0101]
(3)本发明通过机器人模拟犬类动物对角小跑运动的步态，解决了一些仿生机器人灵活度不够与参照性不强的问题。
附图说明
[0102]
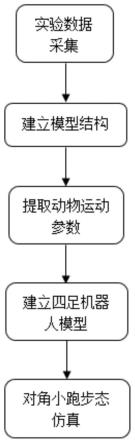
图1是本发明的方法流程图；
[0103]
图2是dpnet模型的结构图；
[0104]
图3(a)是生物狗四肢髋关节的平均角度图；
[0105]
图3(b)是生物狗四肢膝关节的平均角度图；
[0106]
图4是本发明中机器人坐标系设定图；
[0107]
图5是本发明中仿生机器人的单腿坐标系建立图；
[0108]
图6是本发明中基于摆线的四足仿生机器人足端轨迹；
[0109]
图7是本发明中基于贝塞尔曲线的四足仿生机器人足端轨迹；
[0110]
图8是本发明中实际的四足仿生机器人足端轨迹；
[0111]
图9(a)是本发明中机器人在x轴方向的行进速度与加速度曲线图；
[0112]
图9(b)是本发明中机器人在y轴方向的行进速度与加速度曲线图；
[0113]
图9(c)是本发明中机器人在y轴方向的行进速度与加速度曲线图。
具体实施方式
[0114]
下面结合附图和实施例对本发明作进一步详细说明，本实施例仅用于对本发明作出具体说明，本发明保护范围不局限于所述内容。
[0115]
实施例1：一种基于视觉的四足仿生机器人模拟动物步态的方法，如图1所示，所述方法步骤如下：
[0116]
步骤(1)实验数据采集：采用摄影机拍摄泰迪犬类在小区道路上的对角小跑的奔跑视频：拍摄视频中图片分辨率为1270
×
720，拍摄设备与四足动物持平且距离四足动物5-8m，拍摄角度在
±
270
°
之间，在早上8：00-12：00，下午13： 00-18：00之间共拍摄十段1min的视频；
[0117]
步骤(2)建立模型结构：在hrnet高分辨率基础网络上进行改进，建立模型；如图2所示，模型建立的具体步骤如下：
[0118]
在hrnet高分辨率基础网络输出的最后四个分支后面添加两条路径，第一条路径设置为三层混合空洞卷积，第二条路径设置为含有通道和空间两种注意力机制的模块；
[0119]
其中第一条路径具体为：共由三层卷积操作组成，基于第一分支与第二分支通道数较少且上下文全局信息较多的表现，选择在前两个输出分支后面添加 hdc层，假设空洞卷积率为d，网络中原始卷机核尺寸为k
×
k，那么空洞卷积核大小n为
[0120]
n＝k+(k-1)
×
(d-1)
ꢀꢀꢀꢀꢀꢀ
(1)
[0121]
由于空洞卷积在扩大特征信息感受野的同时会出现特征像素读取失去连续性的现象，参与卷积运算的像素点均为膨胀后卷积核的有效权重位置，这样会引起栅格效应，丢失部分有价值的特征信息从而影响到最终网络分类预测的准确性，故采用不同膨胀系数的空洞卷积并将三层卷积操作结合为一条路径，其中为了最大限度地填充丢失部分的像素点从而确保信息表征的全面性，需满足在当前层的最大膨胀系数不大于网络原始卷积核尺寸，即满足条件
[0122]
mi≤k
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0123]
mi＝max[m
i+1-2di,m
i+1-2(m
i+1-di),di]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0124]
其中，mi为第i层的最大膨胀系数，di为第i层的空洞卷积率，max为取三层中的最大值，由此可改进前两个分支中普通常规卷积带来的特征表征能力较弱与信息全局性较差两个方面；
[0125]
第二条路径具体为：在第三分支与第四分支的输出后面添加并行注意力模块 pam，基于后两分支通道数较多故所携带的图像细节信息较全面的特点，将通道注意力机制与空间注意力机制相融合，从而为不同通道的表征和像素的位置分配相应的权重，使得与分类有关的像素点信息在网络训练中更加突出，后两分支的输出特征经过最大池化、平均池化与中值池化的操作后将得到的特征向量进行通道和空间的权值计算；先采用1
×
1的卷积调整通道数为256并进行数据批标准化，在两种注意力机制组合输出的特征向量后降低维度，最后通过sigmoid激活获取并分配2个分支0-1的权重值，生成的通道与空间注意力图计算如下：
[0126]
out
channel
＝w(mlp*(in
avgpool
+in
maxpool
+in
medpool
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0127]
out
spatial
＝w(f*(in
avgpool
,in
maxpool
,in
medpool
))
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(5)
[0128]
[0129]
上式中out
channel
为通道注意图，out
spatial
为空间注意力图，w为sigmoid激活函数，mlp为多层感知机，用以共享权值，f为3
×
3的卷积操作，in表示后两分支的输出特征，out
branch
为通道权重和空间权重分别与输出特征对位相乘再相加得到的最终分支特征；
[0130]
两条路径经过特征融合将低级特征弥补上语义信息同时把高级特征增添上空间信息；
[0131]
通过以上对hrnet高分辨率基础网络的改进，先获得了四足动物的关节点位置再逐次连接形成了骨架模型。
[0132]
步骤(3)提取动物运动参数：通过模型预测四足动物关键点的位置，实现对四足动物运动参数的提取；具体步骤如下：
[0133]
①
同侧步距参数：
[0134]
在模型中获取研究对象一个步态周期内四个角点的坐标位置后，通过定位每一肢踝关节离图像原点距离最远和最近时的两关节坐标欧氏距离变化，计算四肢踝关节相对本身迈步距离的平均值，假设分别为第fi帧和第f
i+1
帧图像中动物左前肢踝关节坐标，则为动物右前肢踝关节坐标，为动物左后肢踝关节坐标，为动物右后肢踝关节坐标，步距计算式为
[0135][0136]
式中为图片像素与实际距离的转换系数，本实施例将动物四肢在一个周期内前进的距离求和并取平均值得到步距，如表1所示；
[0137]
表1泰迪犬类对角小跑同侧步距参数
[0138][0139]
②
关节角度参数：
[0140]
选取标注的关键点3即左前肢膝关节点，将三种研究对象在连续运动周期内膝关节的变化做对比分析，假设模型最终识别的动物髋关节坐标为(xa,ya)，膝关节坐标为(xb,yb)，踝关节坐标为(xc,yc)，则基于关节两点之间的坐标变化，通过坐标向量的平方差可求得a，b，c三个距离，关节计算式为
[0141][0142][0143][0144][0145]
通过式(8)-式(11)计算得到动物的关节角度变化参数。
[0146]
步骤(4)建立四足机器人模型：仿照狗的生物特性设计机器人整体结构，然后通过d-h参数方法进行正运动学建模，使用拉格朗日方程法对机器人的动能与势能进行计算，解得拉格朗日方程以获取机器人每个关节的力矩，再对机器人前进的理想状态下足端轨迹进行规划；具体步骤如下：
[0147]
①
机器人机体结构设计：
[0148]
通过对狗身体骨骼与肌肉纹理的分析，并结合犬类在奔跑运动中的特性，本文选择使用全肘式机械结构作为仿生犬机器人的机体结构。本发明在连接第一段与第二段的髋关节处设置一个自由度，在连接第二段与第三段的膝关节处设置一个自由度，则基于仿生犬机器人的四肢共有八个自由度。
[0149]
基于双路径网络提取到犬类关节角度如图3所示。由图3(a)和图3(b) 可看出泰迪犬四肢髋关节平均角度在20
°‑
90
°
之间，四肢膝关节平均角度主要集中在40
°‑
170
°
范围内，本实施例对犬类进行了实际测量，通过对实体尺寸的观测得到生物狗的各部位长度信息，故由此总结出生物狗的各部位信息如表1 所示。
[0150]
表1仿生犬机器人的体型参数
[0151][0152]
②
机器人运动学建模
[0153]
本发明机器人包含世界坐标系{w}，机体坐标系{b}，腿部坐标系{l}；其中腿部坐标系又包含髋关节坐标系{1}和膝关节坐标系{2}以及足端坐标系{3}，整体机器人的坐标系设定图如图4所示；d-h参数表如下表所示。
[0154]
表2 d-h参数表
[0155][0156]
通过d-h参数计算机器人设置的坐标系中相邻两个系的坐标变换矩阵，经过相邻两个坐标系的平面平移和空间旋转过程后，总体变换矩阵公式为
[0157][0158]
其中，表示第n个坐标系和第n+1个坐标系之间的坐标变换矩阵，rot ()和trans表示经过经过了x轴与z轴的旋转和平移操作，xi表示x轴，αi表示在坐标系空间中的旋转角度，θi为关节坐标系旋转的角度，ai表示两关节点之间的连杆长度，di表示第i个坐标系与第i+1个坐标系之间的偏移距离；
[0159]
将表2中的参数带入到式(10)得到
[0160][0161]
其中坐标系相对于z轴进行旋转变换的旋转矩阵为
[0162][0163]
坐标系相对于x轴进行平移变换的平移矩阵为
[0164][0165]
由式(14)与式(15)可得四足仿生机器人的足端坐标系{3}相对于机体坐标系{b}的坐标变换矩阵如下
[0166][0167]
由于t坐标变换矩阵可简写为以下公式
[0168][0169]
上式中为旋转矩阵，为平移矩阵，由上文发明可知机器人设定的髋关节与膝关节之间的连杆长为20cm，膝关节与踝关节之间的连杆长为18cm，则由式(17)得到四足仿生犬机器人的正运动学建模公式为
[0170][0171]
③
机器人动力学分析
[0172]
结合上文结果，本发明选用拉格朗日方程法分析机器人八个连杆具有的动能与势能，对四足仿生机器人的单腿坐标系建立如图5所示。假设连杆1和连杆2 的质量分别为m1和m2，由此能够得到连杆1和连杆2的转动惯量如下
[0173][0174][0175]
然后分别取连杆的中心点作为质心，确定连杆1和连杆2的质心位置后对x 与y方向上计算质心坐标，公式为
[0176][0177]
[0178]r2x
＝l
1 cos(θ1(t))+(l2cos((θ1(t)+θ2(t)))/2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(23)
[0179]r2y
＝l
1 sin(θ1(t))+(l2sin((θ1(t)+θ2(t)))/2
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(24)
[0180]
两个连杆的速度结果为
[0181][0182][0183]
机器人总动能e为连杆1和连杆2的动能之和，公式结果为
[0184][0185]
机器人总势能为两连杆的势能之和，计算结果为
[0186][0187]
由拉格朗日方程可知，拉格朗日函数等于机器人动能与势能的差
[0188][0189]
基于拉格朗日函数l分别对θ1,θ2,求偏导，将机器人角加速度与机器人关节力矩τ1,τ2的关系通过矩阵表示出来，则更加直观的看到关系矩阵的变化为
[0190][0191]
④
机器人足端轨迹规划
[0192]
采用复合摆线与贝塞尔曲线的方法，将一个运动周期内机器人足端起始点与落地点之间的曲线进行规划。复合摆线的计算公式为
[0193]
[0194][0195][0196]
式(31)为四足仿生机器人的摆动相在x与z方向的轨迹，式(32)为四足仿生机器人的支撑相在x与z方向的轨迹，其中xf与xs分别为机器人在x 轴方向的落足点与起步点，zs为机器人在z轴的起步点，式(33)中tf为机器人处于支撑相的时间，t表示一个运动周期；
[0197]
贝塞尔曲线是由很多控制点通过递归的形式逐渐生成的，贝塞尔曲线与复合摆线相比具有更好的速度与加速度连续性，本发明采用三阶的贝塞尔曲线进行机器人路径规划，公式为
[0198]
b(t)＝p0(1-t)3+3p1t(1-t)2+3p2t2(1-t)+p3t3,t∈[0,1]
ꢀꢀꢀꢀꢀꢀ
(34)
[0199]
式(34)中p0，p1，p2，p3为曲线的四个控制点，设置四个控制点分别为机器人起步点(-0.11,-0.36)，最高点(0,-0.27)，次高点(0.05,-0.28)，落地点 (0.11,-0.36)，通过调节控制点以获取更优的足端轨迹，
[0200]
如图6所示是本发明中基于摆线的四足仿生机器人足端轨迹，如图7所示是本发明中基于贝塞尔曲线的四足仿生机器人足端轨迹，如图8所示是实际的四足仿生机器人足端轨迹。通过图6与图7可知基于复合摆线与贝塞尔曲线方法的机器人足端轨迹有一定差别。在图8中我们可看出机器人的足端初始位置高度为
ꢀ‑
0.36m，随着系统开始计算轨迹，机器人足端向上抬起至-0.27m左右即开始第一个周期运动，由此可见基于贝塞尔曲线的规划方法更加接近机器人的实际足端轨迹，机器人足端实际的起始点与落地点相比于理想规划点更近。
[0201]
步骤(5)对角小跑步态仿真：对机器人的足端轨迹进行了规划，将规划的理想状态下的轨迹同四足仿生机器人的实际运动轨迹进行对比，得出机器人模型可靠，最后通过matlab对机器人模型进行动物运动状态的模拟，基于simulink 模块分析了机器人质心到原点距离的变化和前进过程中机器人速度与加速度的变化，对角小跑步态仿真的具体步骤如下：
[0202]
①
在matlab r2021a的软件环境下进行实验，操作系统是win10系统，通过simulink功能建立以.slx为后缀的机器人仿真模型，基于simulink library browser工具库中的模块建立四足仿生机器人的整体结构与运动关系。通过 multibody-frames and transforms-world frame建立世界基准坐标系，在其基础上使用工具库中的commonly usedblocks为仿真模型添加滤波器或数据形式转换等基础模块，并通过simulink-sinks-scope为机器人的输出端口添加示波器，通过上述建模过程获取机器人的仿真结果；
[0203]
②
再对机器人的自身位移与速度等行进参数进行分析，在simulink模型中添加偏导模块，连接到机器人zyz三个坐标轴方向的输出端，同时偏导模块另一端接上示波器，得到四足仿生机器人在行进过程中的速度与加速度变化曲线图，如图9所示，图9a是本发明中机器人在x轴方向的行进速度与加速度曲线图，图9b是本发明中机器人在y轴方向的行进速度与加速度曲线图，图9c是本发明中机器人在y轴方向的行进速度与加速度曲线图。
[0204]
上面结合附图对本发明的具体实施方式作了详细说明，但是本发明并不限于上述实施方式，在本领域普通技术人员所具备的知识范围内，还可以在不脱离本发明宗旨的前提下作出各种变化。