一种基于复杂度的空中交通冲突管理方法和装置与流程
本发明涉及空中交通技术领域,具体而言,涉及一种基于复杂度的空中交通冲突管理方法和装置。
背景技术:
空中交通的需求量不断提高,随之造成了许多问题,包括严重的空中交通拥堵,以及空中交通管制员需要承担繁重的工作负荷。要在飞行密度大、冲突性质相对复杂的环境下正确行使防相撞职能,需首先解决冲突探测、冲突解脱和解脱航迹优化三个问题。冲突探测是指根据监视系统提供的飞机的位置、高度、速度、航向、飞行模式等信息,预测将要违反最小间隔标准的冲突航迹。其中,航路空域中水平间隔的标准距离通常是5海里,垂直间隔是1000英尺。冲突解脱和解脱航迹优化则是根据一般性的管制原理和方法规划处理想的飞行轨迹。飞行冲突解脱指探测到飞行存在潜在的冲突后,规划出无碰撞的飞行方案,指导飞机飞行以避免可能发生的碰撞危险。常用的冲突解脱策略为以下三种:①调整航向。只改变飞机的飞行航向角,保持飞行速度大小、航迹倾角和飞行高度不变;②调节速度。只改变飞行速度矢量的数值大小,保持航向角和航迹倾角不变;③改变高度。只改变飞行速度矢量的航迹倾角,保持飞行速度的大小和航向角不变。
世界各国的研究者们做了大量有关自由飞行情况下飞行冲突的探测与解决的研究工作。Reich的飞机碰撞危险模型是本领域较早的研究成果。为了简化数学计算,它将每架航空器假设成尺寸相同的长方体,用参数分别表示飞行器的平均长、宽和高,两机冲突概率即两个长方体之间的碰撞危险在数学上就相当于某一质点与长方体之间的碰撞危险概率。许多学者在Reich模型的基础上进行了类似的研究,他们综合了各种影响飞行安全的不 确定因素。J.Hu等人把风等不确定因素对飞行的影响计入动力学方程,飞机运动模型为确定的轨线方程加上一定比例的布朗运动扰动,在这个形式下,冲突的可能性变为布朗运动从一个时变安全区域逃脱的概率,获得了有限无限范围都适用的近似表达。Lee C.Yang则采用了在轨迹模型中包括了飞机意图信息的概率估计方法,主要是用蒙特卡罗仿真根据飞机飞行意图及各种干扰推测未来飞行轨迹,并进行冲突探测和解脱,着重于意图对轨迹的影响。Mondoloni冲突解脱算法也是基于遗传算法的,可以获得在诸如最短时间、最小油耗或总花费条件下的无冲突飞行方案,已经应用于飞行的爬升、转弯、下降阶段未来6-25分钟内冲突预测,能解决含有一定飞行规划约束的冲突(如到达时间固定),实例证明能使消耗函数达到最优,能简单的和飞行计划最优函数合为一体,但计算比较复杂、耗费时间较多,不能预测短期(5分钟内)的冲突。J.Alliot等人提出基于优先权的最优化算法,给每一架飞机赋予不同的优先权,权值高的飞机在不考虑权值低的飞机的情况下选择出自己认为最优的航线,如此类推,其基本的方法是寻找树的最短路。Lucia Pallottino等提出混合整数规划的算法,即在一般几何构造法上建立冲突避免的约束并把它们公式化为线性约束条件,然后用最优化工具CPLEX解决。Tomlin等应用了非合作博弈理论,得出最优控制规则和结果所描述不安全集边界的微分等式,并采用预先设定的冲突解决策略。Menon等将最优控制理论应用于飞行冲突解决,使用了两种不同的方法。第一种方法以总飞行时间和耗油量的线性模型为消耗函数,使用单目标的SQP(Sequential Quadratic Programming)法和多目标的目标获得法解决。第二种方法运用闭环导航法,以航路偏离为最优函数进行多机冲突解脱。
不过此前的大多数研究文章都着重于某一扇区内部的飞机间隔,而较少从多扇区角度出发来重视飞机轨迹。现行的冲突解脱方法把焦点放在仅仅一个扇区内的交通上,这就很可能对飞行安全造成不利影响,而且还可能造成效率低下的问题,因为参与冲突解脱的众多飞机有可能需要重新规 划它们在后续扇区中的轨迹。伊丹等人(Idan et al)就指出说,减少重新规划的轨迹数量也就减少了计算工作和飞行员的工作负荷,最终也就提高了安全性。
发明人在研究中发现,现有技术中的交通冲突控制方法局限于一个扇区中,无法更精确的实现空中交通的控制。
技术实现要素:
有鉴于此,本发明实施例的目的在于提供一种基于复杂度的空中交通冲突管理方法和装置,以确保进入飞机之间的安全间隔,同时最大程度减少扇区管制员的工作负荷。
第一方面,本发明实施例提供了一种基于复杂度的空中交通冲突管理方法,方法包括:
在检测到目标扇区有进入飞机时,根据进入飞机进入目标扇区后目标扇区中原有飞机对应的管制活动量,绘制目标扇区对应的复杂度的计算图;其中,管制活动量系指为解脱进入飞机带来的任何冲突,目标扇区内的原有飞机做出的航向角改变总量;复杂度的计算图系指目标扇区中包括进入飞机的所有飞机形成的空中交通复杂程度的分布图;
对于复杂度的计算图中的冲突区域,计算冲突区域中的冲突最小的最优路径;
选择最优路径对应的进入点为进入飞机进入目标扇区的最优进入点,以便进入飞机根据最优进入点进入目标扇区。
结合第一方面,本发明实施例提供了第一方面的第一种可能的实施方式,其中,根据进入飞机进入目标扇区后目标扇区中原有飞机对应的管制活动量,绘制目标扇区对应的复杂度的计算图,包括:
按照以下公式计算进入飞机的进入角E和方位角B:其中,二进制变量n1和n2使进入飞机的进入点领域保持为-π≤B≤π且0≤E<2π;E表示进入角;B表示方位角;上标E表示进入飞机;
按照以下公式计算进入飞机的航行轨迹变化曲线: 其中,表示航行轨迹变化曲线的横坐标,表示航行轨迹变化曲线的纵坐标;V表示进入飞机的飞行速度,且该速度为定值;上标I表示目标扇区内的进入飞机;k表示目标扇区内的任意一架飞机;t表示目标扇区内的任意一时间;
根据进入飞机的进入角E、方位角B以及进入飞机的航行轨迹变化曲线,计算绘图函数Φ:其中,Φ表示绘图函数;
根据计算的绘图函数,绘制目标扇区对应的复杂度的计算图。
结合第一方面的第一种可能的实施方式,本发明实施例提供了第一方面的第二种可能的实施方式,其中,对于复杂度的计算图中的冲突区域,计算冲突区域中的冲突最小的最优路径,包括:
对于复杂度的计算图中的冲突区域,按照混合整数线性规划对应的计算公式计算目标扇区内原有飞机的航向角改变量Δθ: for k=2,…N;
根据原有飞机的航向角改变量Δθ,计算冲突区域中的冲突最小的最优路径。
结合第一方面的第二种可能的实施方式,本发明实施例提供了第一方面的第三种可能的实施方式,其中,根据计算的绘图函数,绘制目标扇区对应的复杂度的计算图,包括:
采用方差四叉树绘图算法对绘图函数进行求解,以根据求解结果绘制目标扇区对应的复杂度的计算图。
结合第一方面的第三种可能的实施方式,本发明实施例提供了第一方面的第四种可能的实施方式,其中,采用方差四叉树绘图算法对绘图函数进行求解,以根据求解结果绘制目标扇区对应的复杂度的计算图,包括:
第1步:将X-Y坐标系中的表示进入飞机的进入点的圆弧转换为E-B坐标系中的四方形;
第2步:按照四方形的网格尺寸δ来划分搜索空间S;
第3步:计算每个离散点(E、B)上的管制活动量C,并绘制对应的复杂度;
第4步:将复杂度转换成二进制点阵,其中每个点都有两种表达式:C=0或≠0(即C=1);
第5步:针对空间S中每一个四方格来计算方差Q;方差Q的计算方法包括:
第6步:重复第3-5步,直至细分区域中的所有Q都为零,或是直至网格尺寸缩小到被设定为1度的最小网格尺寸为止;
第6步对应的绘制的复杂度即为最终的目标扇区对应的复杂度的计算图。
结合第一方面的第三种可能的实施方式或第四种可能的实施方式,本发明实施例提供了第一方面的第五种可能的实施方式,其中,表示进入飞机的进入点的圆弧通过以下方法得到:
获取目标扇区边界上,进入飞机可以到达的进入点P1和P2;
确定进入点P1和P2对应的圆弧为表示进入飞机的进入点的圆弧;其中,Ps和Pf分别为进入飞机在时间t=0和t=T时的位置;圆弧对应的进入角E的范围是:EP1≤E≤EP2。
结合第一方面的第二种可能的实施方式,本发明实施例提供了第一方 面的第六种可能的实施方式,混合整数线性规划对应的计算公式 for k=2,…N的计算方法,包括:
根据以下公式计算目标扇区内所有冲突得到解脱的每架飞机的航向角θi:其中和Δθi分别代表每架飞机的初始航向角和航向角变化量;
根据以下公式计算目标扇区内每架飞机的相对航向角:qa/b=θa-ψab+2πsgn(ψab)bab,qb/a=θb-ψab+2πsgn(ψab)bba;其中,ψab是飞机与横轴之间连线的角度,bab和bba是范定以下域的二进制变量:-π≤qa/b≤π,-π≤qb/a≤π;
根据以下公式计算目标扇区内每两架飞机之间发生冲突所必需的最小安全角θm:其中,Dab系指两架飞机之间的距离,r则是两架飞机之间的安全半径;
根据目标扇区内每架飞机的相对航向角θi、每架飞机的相对航向角和最小安全角θm,得到混合整数线性规划对应的计算公式 for k=2,…N。
第二方面,本发明实施例还提供了一种基于复杂度的空中交通冲突管理装置,所述装置包括:
复杂度图绘制模块,用于在检测到目标扇区有进入飞机时,根据进入飞机进入目标扇区后目标扇区中原有飞机对应的管制活动量,绘制目标扇区对应的复杂度的计算图;其中,管制活动量系指为解脱进入飞机带来的任何冲突,目标扇区内的原有飞机做出的航向角改变总量;复杂度的计算图系指目标扇区中包括进入飞机的所有飞机形成的空中交通复杂程度的分布图;
最优路径计算模块,用于对于复杂度的计算图中的冲突区域,计算冲突区域中的冲突最小的最优路径;
最优进入点选择模块,用于选择最优路径对应的进入点为进入飞机进入目标扇区的最优进入点,以便进入飞机根据最优进入点进入目标扇区。
结合第二方面,本发明实施例提供了第二方面的第一种可能的实施方式,其中,复杂度图绘制模块,包括:
第一计算单元,用于按照以下公式计算进入飞机的进入角E和方位角B:其中,二进制变量n1和n2使进入飞机的进入点领域保持为-π≤B≤π且0≤E<2π;E表示进入角;B表示方位角;上标E表示进入飞机;
第二计算单元,用于按照以下公式计算进入飞机的航行轨迹变化曲线: 其中,表示航行轨迹变化曲线的横坐标,表示航行轨迹变化曲线的纵坐标;V表示进入飞机的飞行速度,且该速度为定值;上标I表示目标扇区内的进入飞机;k表示目标扇区内的任意一架飞机;t表示目标扇区内的任意一时间;
第三计算单元,用于根据进入飞机的进入角E、方位角B以及进入飞机的航行轨迹变化曲线,计算绘图函数Φ: 其中,Φ表示绘图函数;
复杂度图绘制单元,用于根据计算的绘图函数,绘制目标扇区对应的复杂度的计算图。
结合第二方面的第一种可能的实施方式,本发明实施例提供了第二方面的第二种可能的实施方式,其中,最优路径计算模块,包括:
第四计算单元,用于对于复杂度的计算图中的冲突区域,按照混合整数线性规划对应的计算公式计算目标扇区内原有飞机的航向角改变量Δθ: for k=2,…N;
第五计算单元,用于根据原有飞机的航向角改变量Δθ,计算冲突区域中的冲突最小的最优路径。
本发明实施例提供的一种基于复杂度的空中交通冲突管理方法和装置,包括:在检测到目标扇区有进入飞机时,根据进入飞机进入目标扇区后目标扇区中原有飞机对应的管制活动量,绘制目标扇区对应的复杂度的计算图;对于复杂度的计算图中的冲突区域,计算冲突区域中的冲突最小的最优路径;选择最优路径对应的进入点为进入飞机进入目标扇区的最优进入点,以便进入飞机根据最优进入点进入目标扇区,与现有技术中的交通冲突控制方法局限于一个扇区中,无法更精确的实现空中交通的控制相比,其当飞机进近某一扇区时,绘制进入飞机在每一点扇区进入点进入目标扇区的复杂度计算图,并根据复杂度计算图找到进入飞机的最优进入点,使用复杂度提供的空中交通如何对进入飞机作出反应方面的详细信息,飞机进入点就能得到修正,能够最大程度减少扇区内的冲突,以确保进入飞机之间的安全间隔,同时最大程度减少扇区管制员的工作负荷。
为使本发明的上述目的、特征和优点能更明显易懂,下文特举较佳实施例,并配合所附附图,作详细说明如下。
附图说明
为了更清楚地说明本发明实施例的技术方案,下面将对实施例中所需要使用的附图作简单地介绍,应当理解,以下附图仅示出了本发明的某些实施例,因此不应被看作是对范围的限定,对于本领域普通技术人员来讲,在不付出创造性劳动的前提下,还可以根据这些附图获得其他相关的附图。
图1示出了本发明实施例所提供的一种基于复杂度的空中交通冲突管理方法的流程图;
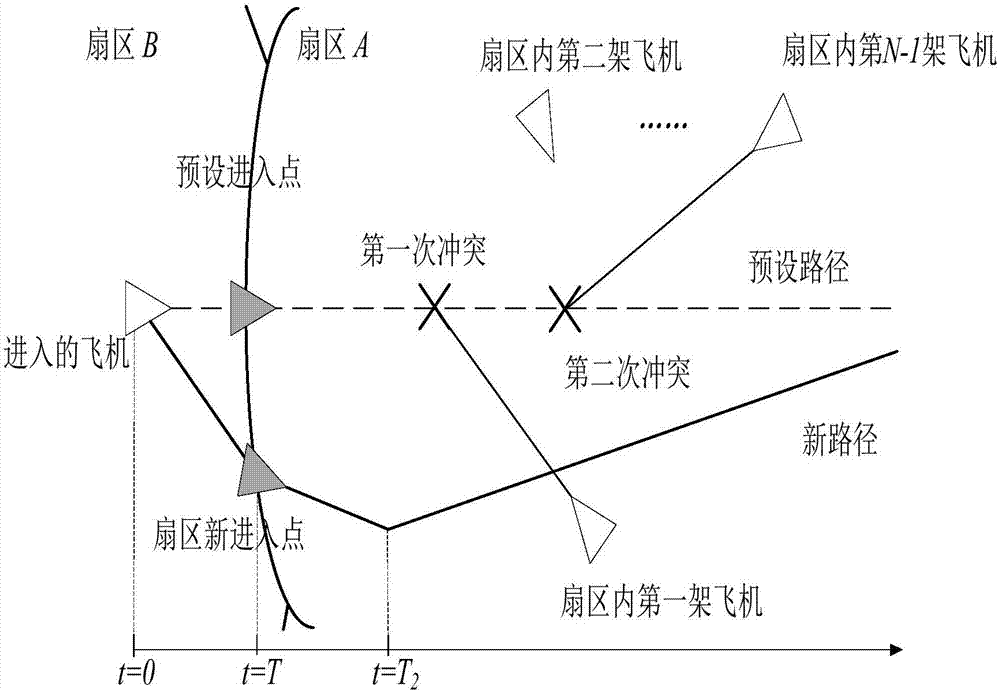
图2示出了本发明实施例所提供的一种基于复杂度的空中交通冲突管理方法中的操作概念的示意图;
图3示出了本发明实施例所提供的一种基于复杂度的空中交通冲突管理方法中的进入角E和方位角B的定义的示意图;
图4示出了本发明实施例所提供的一种冲突解脱办法几何图;
图5示出了本发明实施例所提供的X-Y坐标系和E-B坐标系中可以到达的进入点的示意图;
图6示出了本发明实施例所提供的网格以及相邻离散点的界定的示意图;
图7示出了本发明实施例所提供的2级细化示例的示意图;
图8示出了本发明实施例所提供的某种抽样的空中交通状况,其中有5架飞机,扇区半径为170海里的示意图;
图9示出了本发明实施例复杂度的算法、经过0-3级细化的复杂度的示意图;
图10示出了本发明实施例所提供的一种基于复杂度的空中交通冲突管理装置的结构示意图。
具体实施方式
为使本发明实施例的目的、技术方案和优点更加清楚,下面将结合本发明实施例中附图,对本发明实施例中的技术方案进行清楚、完整地描述,显然,所描述的实施例仅仅是本发明一部分实施例,而不是全部的实施例。通常在此处附图中描述和示出的本发明实施例的组件可以以各种不同的配置来布置和设计。因此,以下对在附图中提供的本发明的实施例的详细描述并非旨在限制要求保护的本发明的范围,而是仅仅表示本发明的选定实施例。基于本发明的实施例,本领域技术人员在没有做出创造性劳动的前提下所获得的所有其他实施例,都属于本发明保护的范围。
本发明实施例提供的一种基于复杂度的空中交通冲突管理方法和装置,使得飞机(即下面的进入飞机)在到达下一个扇区边界之前就改变其的进入点。其中,上述进入点是以依据复杂度来最大程度减少与下一个扇 区内其它飞机之间的冲突为条件来判定的。上述复杂度系指一种空中交通复杂性评估方法,其体现了依据进入飞机的情况来掌控扇区内的冲突所需要的工作量。本发明实施例中的复杂度是对扇区(即目标扇区)内已知的交通流将如何响应进入飞机而提供对交通流管理相当重要的详细信息。本发明实施例中提出了如何在某一扇区内增加一架飞机时尽可能减少对扇区内飞机带来的交通复杂性的问题,并依据杜宾斯路径(Dubins path)来为进入飞机设计了一条可以飞行的路径,并将该研究扩大到了多种实际应用中。
参见图1,本发明实施例提供了一种基于复杂度的空中交通冲突管理方法,所述方法包括:
S101、在检测到目标扇区有进入飞机时,根据所述进入飞机进入所述目标扇区后所述目标扇区中原有飞机对应的管制活动量,绘制所述目标扇区对应的复杂度的计算图;其中,所述管制活动量系指为解脱所述进入飞机带来的任何冲突,所述目标扇区内的原有飞机做出的航向角改变总量;所述复杂度的计算图系指所述目标扇区中包括所述进入飞机的所有飞机形成的空中交通复杂程度的分布图。
具体的,为了从图形上来展示管制活动量C,基于复杂度图对管制活动量C,作出如下定义,以便对扇区内飞机的冲突解脱机动操纵进行量化。
定义1:管制活动量C系指为解脱某架进入飞机带来的任何冲突而让扇区内飞机作出的航向角改变总量。
S102、对于所述复杂度的计算图中的冲突区域,计算所述冲突区域中的冲突最小的最优路径。
具体的,复杂度的计算图包括进入飞机带来的冲突区域和无冲突区域;本发明实施例中,不考虑无冲突区域;而针对冲突区域,计算当前进入飞机进入目标扇区后管制活动量C,即计算解脱当前进入飞机进入目标扇区 后,带来的任何冲突而让扇区内飞机作出的航向角改变总量。
S103、选择所述最优路径对应的进入点为所述进入飞机进入所述目标扇区的最优进入点,以便所述进入飞机根据所述最优进入点进入所述目标扇区。
本发明实施例提供的一种基于复杂度的空中交通冲突管理方法,与现有技术中的交通冲突控制方法局限于一个扇区中,无法更精确的实现空中交通的控制相比,其当飞机进近某一扇区时,绘制进入飞机在每一点扇区进入点进入目标扇区的复杂度计算图,并根据复杂度计算图找到进入飞机的最优进入点,使用复杂度提供的空中交通如何对进入飞机作出反应方面的详细信息,飞机进入点就能得到修正,能够最大程度减少扇区内的冲突,以确保进入飞机之间的安全间隔,同时最大程度减少扇区管制员的工作负荷。
具体的,在当前的空中交通管制系统中,冲突解脱办法针对的是处在某一扇区内的飞机。如果某架新来的飞机进近这一扇区,那么系统就只是在它到达扇区边界之后才开始设法确保它与别的飞机之间的最小间隔。其实如果进近飞机能够主动采取行动,那就有可能改善管理冲突的效果,而采取这类主动行动的常见方法就是调整某一固定进入点的进场时间。人们尤其对通过调整进入飞机的速度来实现的进场管理开展了大量研究,以期减轻机场空域中的拥堵状况。但是很少有人研究改变进入点的可能性。本发明实施例则放弃预先确定的进入点,而以动态方式来确定进入飞机的替代性进入点,以此来最大程度减少冲突。研究证明,只要对新进场飞机的扇区进入点作出小幅改变,为保持飞机之间的间隔而要求的航向角改变量就会显著减少。
本发明实施例以图2中的两个空域(分别命名为扇区A和扇区B)来说明所提出的操作概念。扇区A内有N-1架飞机在飞行,交通的初始状况是无冲突。在时间t=0时,一架飞机从扇区B进近扇区A,预计进场 时间是t=T。假定这架进入飞机会造成与扇区A内其它飞机之间的冲突。按照常规的空中交通管制方法,管制系统只在时间t=T之后才开始设法解脱进入飞机带来的冲突。相邻扇区的管制员也可以通过密切协调来解脱冲突,但是这样的协调仅限于战术层级,而且只在进入飞机带来的冲突十分紧迫的情况下才会进行。按照本发明实施例提出的方法,进入飞机首先就预见到t=T时扇区A内的空中交通状况,并在到达扇区边界之前就判定一个合适的进入点。此外在时间t=T2时,此外在所有冲突都得到解脱后,进入飞机要执行恢复机动,以飞向它的初始目的地。
进一步的,上述步骤101中具体绘制复杂度的计算图的方法包括:
按照以下公式计算所述进入飞机的进入角E和方位角B:其中,二进制变量n1和n2使所述进入飞机的进入点领域保持为-π≤B≤π且0≤E<2π;E表示进入角;B表示方位角;上标E表示进入飞机;
按照以下公式计算所述进入飞机的航行轨迹变化曲线:其中,表示航行轨迹变化曲线的横坐标,表示航行轨迹变化曲线的纵坐标;V表示所述进入飞机的飞行速度,且该速度为定值;上标I表示所述目标扇区内的所述进入飞机;k表示所述目标扇区内的任意一架飞机;t表示所述目标扇区内的任意一时间;
根据所述进入飞机的进入角E、方位角B以及所述进入飞机的航行轨迹变化曲线,计算绘图函数Φ:其中,Φ表示绘图函数;
根据计算的所述绘图函数,绘制所述目标扇区对应的复杂度的计算图。
具体的,以图3所示的圆形边界以内的空域为例。复杂度是两项参数所决定的结果,其一是进入角E,其二是方位角B。从图3中可以看出,进入角E以从北方进入的角坐标来规定,而方位角B则相对于进入飞机与扇区中心相连的径向线来描述了进入飞机的相对轨迹。
本发明实施例采用了以下假设条件来说明所提出通过定义管制活动量C来绘制复杂度的计算图,并以此来进行空中交通冲突管理的方法。首先,所有飞机在二维空域中按不变速度V来移动。其次,当每架飞机的安全环区(半径为2.5海里的圆形区域)交叠时,便会产生两架飞机之间的冲突。第三,每架飞机可以为避开冲突而改变一次航向角。第四,飞机以一种运动学模型来表示,可以迅即改变航向角。
针对所有进入角E和方位角B的组合来绘制复杂度时所需要的管制活动C可以通过以下两个步骤来判定。本发明实施例以处在(XE(0),YE(0))位置上的一架进入飞机为例。第一步是判定从(XE(T),YE(T))这一位置上开始的进入角E和方位角B以及进入飞机的航向角θE(T)。注意T代表进入飞机抵达扇区边界的时间,而这一时间T要取决于进入点(E、B),因为进入飞机按照不变速度V来飞行,这一点在前文中已经交代过。如果扇区中心处在初始位置,那么(E、B)与(XE(T),YE(T),θE(T))之间的关系就可以表达为以下公式:
其中,上述公式(1)和(2)中,上标E表示进入飞机,另外我们代入了二进制变量n1和n2来让域保持为-π≤B≤π且0≤E<2π。第二步是判定扇区内飞机在时间t=T时的位置和航向角。扇区内第k架飞机的运动学模型可以表达为以下公式:
其中,上标I表示扇区内飞机。
依据这些信息,我们就能对绘图函数Φ作出如下定义:
要得出管制活动量C,需要制订一种冲突解脱算法。管制活动量C取决于选择哪一种冲突解脱算法,而当前有多种不同的算法可供选择。不过为说明起见,本发明实施例提出了一种特殊的冲突解脱算法,也就是以混合整数线性规划为基础的按序冲突解脱算法。
我们要用这种按序算法算出每架飞机的航向角改变量Δθ,从而使所有冲突都能通过新的航向角θ(θ=θ0+Δθ)来解脱,其中,θ0为每架飞机的初始航向角。我们可以针对扇区内有两架飞机的情况来作出几何学考虑,在此基础上推导出无冲突的条件,然后将这种条件延伸到N架飞机的一般情况中。在解决冲突的按序算法中,绩效指数是为最大程度减少每架飞机的航向角改变量Δθ来确定的。此外我们还从无冲突条件中推导出了约束条件。解脱冲突的按序算法的详细公式具体在下面说明。这里要注意的是,本发明实施例提出的方法并不排除其它类型的冲突解脱算法。
进一步的,上述步骤102中,对于所述复杂度的计算图中的冲突区域,计算所述冲突区域中的冲突最小的最优路径的具体方法包括:
对于所述复杂度的计算图中的冲突区域,按照混合整数线性规划对应的计算公式计算所述目标扇区内原有飞机的航向角改变量Δθ: for k=2,…N。
根据所述原有飞机的航向角改变量Δθ,计算所述冲突区域中的冲突最小的最优路径。
而上述混合整数线性规划对应的计算公式 for k=2,…N的是根据如下方法计算得到的:
根据以下公式计算所述目标扇区内所有冲突得到解脱的每架飞机的航向角θi:其中和Δθi分别代表每架飞机的初始航向角和航向角变化量;
根据以下公式计算所述目标扇区内每架飞机的相对航向角:qa/b=θa-ψab+2πsgn(ψab)bab,qb/a=θb-ψab+2πsgn(ψab)bba;其中,ψab是飞机与横轴之间连线的角度,bab和bba是范定以下域的二进制变量:-π≤qa/b≤π,-π≤qb/a≤π;
根据以下公式计算所述目标扇区内每两架飞机之间发生冲突所必需的最小安全角θm:其中,Dab系指两架飞机之间的距离,r则是两架飞机之间的安全半径;
根据所述目标扇区内每架飞机的相对航向角θi、每架飞机的相对航向角和所述最小安全角θm,得到所述混合整数线性规划对应的计算公式 for k=2,…N。
具体的,上述过程即解脱冲突的按序算法的详细公式的推导过程,即判定控制活动量C的优化问题:
依据几何考虑的无冲突条件是按照以下方法来推导的。首先我们考虑有两架飞机的情况,之后再采用有N架飞机的一般情况。如果以下条件之一得到满足,那么飞机a和b之间就没有冲突。
条件1:
qa/b≥0,qb/a≥0,qa/b≥qb/a (6)
条件2:
qa/b≥0,qb/a≤0,qa/b≤qb/a (7)
条件3:
qa/b≥0,qb/a≤0,qa/b≥-qb/a (9)
条件4:
qa/b≥0,qb/a≤0,qa/b≤-qb/a (10)
条件5:
qa/b≤0,qb/a≥0,-qa/b≥qb/a (12)
条件6:
qa/b≤0,qb/a≥0,-qa/b≤qb/a (13)
条件7:
qa/b≤0,qb/a≤0,-qa/b≥-qb/a (15)
条件8:
qa/b≤0,qb/a≤0,-qa/b≤-qb/a (16)
其中,qa/b和qb/a是相对的航向角,θa和θb是绝对航向角。要注意让所有冲突得到解脱的每架飞机的航向角θi是按以下公式来算出的:
其中,和Δθi分别代表每架飞机的初始航向角和航向角变化量。相对航向角可以按以下公式来算出:
qa/b=θa-ψab+2πsgn(ψab)bab (19)
qb/a=θb-ψab+2πsgn(ψab)bba (20)
其中ψab是飞机与横轴之间连线的角度,bab和bba则是范定以下域的二进制变量:
-π≤qa/b≤π,-π≤qb/a≤π (21)
此外,θm是避免两架飞机之间发生冲突所必需的最小安全角,本发明实施例可以用以下公式来算出这个角度:
其中Dab系指这两架飞机之间的距离,r则是安全半径,如图4所示。
采用本发明实施例提出的冲突解决按序算法来得出控制活动量C的数值。这是因为在现实中,空中交通管制员一次只能对一架飞机下达改变机动操纵的指令,之后要在一定的时间间隔后空中交通管制员才能下令让另一家飞机改变它的机动操纵,因此冲突解脱办法就必然是要按序进行的。要注意在按序冲突解脱算法中,我们自西向东地对飞机排序。此外如果两架飞机的位置是彼此垂直的,那就为最南边的飞机指派数字更小的序号。“1”这个数字最小的编号指派给进入飞机,最后我们就可以按照混合整数线性规划来表达第k架扇区内飞机的冲突解脱问题:
对于N架飞机的情况,以上针对第k架扇区内飞机的优化问题要运算N-1次来解答。例如对于这一冲突解脱办法的问题,我们首先相对于固定不变的进入飞机来判定第一架扇区内飞机最低的管制活动量Δθ2。在第一架扇区内飞机改变航向角后,我们算出第二架扇区内飞机的管制活动量Δθ3,以满足与固定的进入飞机和第一架扇区内飞机之间无冲突的条件。通过上述步骤,我们便给出每道题的答案Δθ2,Δθ3,…和ΔθN。接下来就可以算出以航向角变化总量的来表示的管制活动量C,也就是
在判定扇区边界上新的替代性进入点时就要采用复杂度。复杂度即,依据这架飞机(即进入飞机)所有可能的进入点,解脱进入飞机带来的冲突需要多少管制活动。根据这样的信息,我们就能以最低限度的管制活动来判定出最优进入点。本发明实施例提出了进入点决策算法,并以此来确 定可行性最高的进入点,而不是固守初始进入点。此外,本发明实施例还提出了绘制复杂度时改善计算效率的一种方法,其中考虑了航图的可变网格结构和飞机的机动能力。
进一步的,步骤101计算得到的绘图函数考虑的是理想状态,但是,理想状态对应的求解过程非常复杂,对此,本发明实施例提供了一种针对绘图函数求解算法,减少其计算量,可操作性较好,具体方法包括:
采用方差四叉树绘图算法对所述绘图函数进行求解,以根据求解结果绘制所述目标扇区对应的复杂度的计算图;上述采用方差四叉树绘图算法对所述绘图函数进行求解,以根据求解结果绘制所述目标扇区对应的复杂度的计算图,具体包括:
第1步:将X-Y坐标系中的表示进入飞机的进入点的圆弧转换为E-B坐标系中的四方形;上述表示进入飞机的进入点的圆弧通过以下方法得到:获取所述目标扇区边界上,所述进入飞机可以到达的进入点P1和P2;确定所述进入点P1和P2对应的圆弧为表示所述进入飞机的进入点的圆弧;其中,Ps和Pf分别为进入飞机在时间t=0和t=T时的位置;所述圆弧对应的进入角E的范围是:EP1≤E≤EP2。
第2步:按照所述四方形的网格尺寸δ来划分搜索空间S;
第3步:计算每个离散点(E、B)上的管制活动量C,并绘制对应的复杂度;
第4步:将复杂度转换成二进制点阵,其中每个点都有两种表达式:C=0或≠0(即C=1);
第5步:针对空间S中每一个四方格来计算方差Q;所述方差Q的计算方法包括:
第6步:重复第3-5步,直至细分区域中的所有Q都为零,或是直至网格尺寸缩小到被设定为1度的最小网格尺寸为止;
第6步对应的绘制的复杂度即为最终的所述目标扇区对应的复杂度的计算图。
具体的,本发明实施例中则说明进入点决策算法。在新来的飞机进入某一扇区时就需要这样的决策算法。上面中我们已经解释过,我们在初始的复杂度中考虑了从0到360度的进入角E以及从-90到90度的方位角B。如果以1度的网格尺寸来让这两个角度离散化,那么第(5)号方程式中的混合整数线性规划模型就要经过65,160(=181×360)次运算解答才能绘制出复杂度。加大复杂度上的网格尺寸可以减少所需要的运算,但是复杂度的准确性也会降低,因为它的精度与网格尺寸成反比。为了解决这一问题,本发明实施例便把焦点放在如何快速而准确地绘制复杂度上。本节划分为三部分,每一部分都提出解决这一问题的一种方法。
(一)扇区边界上可以到达的进入点
本发明实施例提出的方法不必考虑进入角E的整个范围、以使0≤E<2π。我们只需考虑扇区边界上对应进入飞机初始位置的、可以到达的进入点,就可以限定进入角E的范围。扇区边界上可以到达的进入点被限定到由P1和P2这两个接触点所决定的一段圆弧上,如图5左图所示,其中Ps和Pf分别为进入飞机在时间t=0和t=T时的位置。X-Y坐标系中的圆弧可以转换为E-B坐标系中的四方形,如图5右图所示。这里要注意,通过考虑可以到达的进入点,我们就可以仅绘制EP1≤E≤EP2这一限定范围内的复杂度,而不必考虑0≤E<2π这整个范围。其中,图5中,左图表示X-Y坐标系中的圆形;右图表示E-B坐标系中的四方形。
随后我们就能对所需计算量的减少幅度作出以下分析。我们以R来表示扇区半径,以d来表示图3所示的Ps和Pf之间的距离。接下来就可以按照以下公式来推算出计算量的减少比率;图5左图中,此外,最大计算次数也可以算出。当E-B坐标系中的四方形按照最小网格尺寸来均匀离散化时,最大计算次数就是网格点的数量。如果将最小网格尺寸规定为那么最大计算次数就可以按照以 下公式来算出:举例而言,如果规定R为200海里,d为30海里,那么计算次数就能减少16.44%。此外,如果规定为1度,那么最大计算次数就大约是11,041次。
虽然本发明实施例主要考虑的是圆形边界,但我们提出的方法可以很方便地应用到任何形状的扇区边界上。只不过在任意形状的扇区边界情况下,则需另外规定两项参数来取代进入角E和方位角B。首先,我们按照从基准点开始沿着扇区边界的位移量来规定飞机的进入点。之后再相对于正北方来规定进入飞机的方位。只要采用这两项参数来取代E和B,就能确定出任意形状的扇区边界的复杂度。后面将给出非圆形扇区边界的示意性复杂度。
(二)以方差四叉树为基础的航图绘制算法
本节介绍了绘制二进制复杂度的方差四叉树绘图算法。最初的方差四叉树算法是一种空间抽样方法,其中一幅图像被划分为四个等分象限,直至层级内的方差被减少到某一规定程度为止。在本发明实施例中,管制活动量C大于0的进入点被视作不合适的进入点。因此在绘制二进制航图时就要陈述C=0是否包含了充足的信息。现在按照一种分级方式,我们的算法首先从覆盖可到达进入点的搜索空间的均匀粗网格开始,然而在某些区域添加更细的次级网格。通过由粗到细地重复这一过程,我们就能绘制出二进制复杂度,并且有效地保留最初的复杂度中的信息。
下面我们以一种单级细化方法为例。单级细化可以扩展到多级细化中。我们以S∈R2来表示搜索空间,也就是图5左图中的方格区域。S这一区域被分隔成尺寸为δ的网格,以绘制复杂度。下一步就可以计算出区域S中每个点(E、B)的管制活动量C。图6示意了网格及其相邻的离散点。四方格顶点上管制活动量的方差Q是判定是否需要进一步划分更细的次级网格的标准。方差Q的计算公式如下:
其中为四方格顶点上管制活动量的平均数。如果Q≠0,那么四方格就被划分成尺寸为的四象限;否则就不需要划分更细的次级网格。图7显示了2级细化的例子。
方差四叉树绘图算法处理流程如下:
第1步:按照网格尺寸δ来划分搜索空间S。
第2步:计算每个离散点(E、B)上的管制活动量C,并绘制对应的复杂度。
第3步:将复杂度转换成二进制点阵,其中每个点都有两种表达式:C=0或≠0(C=1)。换句话说,如果管制活动量C不为零,那么数值就变换为1。
第4步:针对空间S中每一个四方格来计算第(8)号公式中的方差Q。
第5步:重复第2-4步,直至细分区域中的所有Q都为零,或是直至网格尺寸缩小到被设定为1度的最小网格尺寸为止。
这里要注意,在许多进入点(E、B)∈S上的管制活动量C都为零。在所有这些可供选择的进入点中,本发明实施例把距离原始进入点最近的点视作是可行程度最高的进入点。
如图8所示,图8显示了某种抽样的空中交通状况,也就是半径170海里的扇区内有5架飞机;图8中,左图表示初始交通状况,右图表示最终目的地;其中,Y轴(单位为海里);X轴(单位为海里)。在图8左图中,扇区边界被描绘为一个大圆,其中小三角代表在时间t=0时随机指派的飞机初始位置和方向。前文已经讲到,我们按照从西到东的顺序来给每架飞机指定一个编号,而图中的“AC”字样即代表“飞机”。图8右图中的五角星形代表这些飞机在扇区内的最终目的地。当时间t=0时,我们应用所提出的冲突管理方法来解决进入扇区的飞机1带来的冲突。由于进入飞机的路径为解决冲突而偏离了它最初的目的地,因而冲突解决算法在 每一个时间步进量中都要重新运行来算出新的方向,以使所有飞机都能到达它们的最终目的地。在这一设想情境中,如果进入飞机继续向前飞行,那就需要4.61度的控制活动。但是由于让进入飞机飞经按复杂度来判定的替代性进入点,扇区内的飞机就不需要为解决冲突而进行机动操作。图9左1图显示了按照单一均匀网格法来绘制的复杂度,其中的白色区域表示飞机在其中不需要控制活动,而在黑色区域中则有飞机1造成的冲突。图9左2图到9左4图显示了按照我们提出的算法、经过1-3级细化来绘制的复杂度,其中黑色的小圆圈表示最初预定进入点的(进入角、方位角=267,0),这是按照进入飞机的初始位置和方向来判定的;黑色小三角则表示重新判定的进入点的(进入角,方位角=268,-7),其中从最近的进入点到最初进入点之间的控制活动C为零。其中,图9中,B(deg):方位角(度);E(deg):进入角(度)。
本发明实施例提供的一种基于复杂度的空中交通冲突管理方法,与现有技术中的交通冲突控制方法局限于一个扇区中,无法更精确的实现空中交通的控制相比,其当飞机进近某一扇区时,绘制进入飞机在每一点扇区进入点进入目标扇区的复杂度计算图,并根据复杂度计算图找到进入飞机的最优进入点,使用复杂度提供的空中交通如何对进入飞机作出反应方面的详细信息,飞机进入点就能得到修正,能够最大程度减少扇区内的冲突,以确保进入飞机之间的安全间隔,同时最大程度减少扇区管制员的工作负荷。
本发明实施例针对新来的飞机进入扇区的问题来探究了不会给扇区内飞机带来冲突解决活动的可行的进入点。对这类冲突的常规解决方法注重的是扇区内部的最优解脱办法,而我们提出的冲突管理方法则尝试判定多扇区范围内的最佳策略,这或许就能成为将来进一步研究的基础。在提出空中交通管理领域中新的冲突解脱方法的同时,我们也对最初的复杂度概念进行了重新解读与改动。本发明实施例提出的进入点决策算法考虑到了进入飞机的机动能力,并应用了方差四叉树算法,以便更加高效地绘制复杂度。此外我们还展示了数值模拟(包括一种蒙特卡洛模拟)的结果,并在真实交通情境中应用了所提出的方法,以验证它的效果。今后在研究应当扩大这种方法所使用的模型,将我们采用的二维交通模型扩展为三维 模型。此外或许还需要考虑不同的冲突解决机动操纵(例如同时改变航向角和速度的综合机动操纵)。扩展后的模型或许需要不同的优化技巧,例如非线性规划和几何规划,以使它们在计算方面更容易驾驭。我们所提出的方法的效果也还需要在多种交通状况中进一步考察。这种冲突管理的概念亦应经过进一步的完善和检验。此外我们还得要基于此次研究的结果来制订更加切实的空中交通管理规程以及相关决策支持工具的界面,并执行穷尽式的人机共生分析,以进一步验证所提出的方法的适用性。
本发明实施例还提供了一种基于复杂度的空中交通冲突管理装置,所述装置用于执行上述基于复杂度的空中交通冲突管理方法,参考图10,所述装置包括:
复杂度图绘制模块11,用于在检测到目标扇区有进入飞机时,根据进入飞机进入目标扇区后目标扇区中原有飞机对应的管制活动量,绘制目标扇区对应的复杂度的计算图;其中,管制活动量系指为解脱进入飞机带来的任何冲突,目标扇区内的原有飞机做出的航向角改变总量;复杂度的计算图系指目标扇区中包括进入飞机的所有飞机形成的空中交通复杂程度的分布图;
最优路径计算模块12,用于对于复杂度的计算图中的冲突区域,计算冲突区域中的冲突最小的最优路径;
最优进入点选择模块13,用于选择最优路径对应的进入点为进入飞机进入目标扇区的最优进入点。
进一步的,上述基于复杂度的空中交通冲突管理装置,复杂度图绘制模块11,包括:
第一计算单元,用于按照以下公式计算进入飞机的进入角E和方位角B:其中,二进制变量n1和n2使进入飞机的进入点领域保持为-π≤B≤π且0≤E<2π;E表示进入角;B表示方位角;上标E表示进入飞机;
第二计算单元,用于按照以下公式计算进入飞机的航行轨迹变化曲线: 其中,表示航行轨迹变化曲线的横坐标,表示航行轨迹变化曲线的纵坐标;V表示进入飞机的飞行速度,且该速度为定值;上标I表示目标扇区内的进入飞机;k表示目标扇区内的 任意一架飞机;t表示目标扇区内的任意一时间;
第三计算单元,用于根据进入飞机的进入角E、方位角B以及进入飞机的航行轨迹变化曲线,计算绘图函数Φ: 其中,Φ表示绘图函数;
复杂度图绘制单元,用于根据计算的绘图函数,绘制目标扇区对应的复杂度的计算图。
进一步的,上述基于复杂度的空中交通冲突管理装置,最优路径计算模块12,包括:
第四计算单元,用于对于复杂度的计算图中的冲突区域,按照混合整数线性规划对应的计算公式计算目标扇区内原有飞机的航向角改变量Δθ: for k=2,…N。
第五计算单元,用于根据原有飞机的航向角改变量Δθ,计算冲突区域中的冲突最小的最优路径。
本发明实施例提供的一种基于复杂度的空中交通冲突管理装置,与现有技术中的交通冲突控制方法局限于一个扇区中,无法更精确的实现空中交通的控制相比,其当飞机进近某一扇区时,绘制进入飞机在每一点扇区进入点进入目标扇区的复杂度计算图,并根据复杂度计算图找到进入飞机的最优进入点,使用复杂度提供的空中交通如何对进入飞机作出反应方面的详细信息,飞机进入点就能得到修正,能够最大程度减少扇区内的冲突,以确保进入飞机之间的安全间隔。
本发明实施例所提供的基于复杂度的空中交通冲突管理可以为设备上的特定硬件或者安装于设备上的软件或固件等。本发明实施例所提供的装置,其实现原理及产生的技术效果和前述方法实施例相同,为简要描述,装置实施例部分未提及之处,可参考前述方法实施例中相应内容。所属领域的技术人员可以清楚地了解到,为描述的方便和简洁,前述描述的系统、装置和单元的具体工作过程,均可以参考上述方法实施例中的对应过程,在此不再赘述。
在本发明所提供的实施例中,应该理解到,所揭露装置和方法,可以通过其它的方式实现。以上所描述的装置实施例仅仅是示意性的,例如,所述单元的划分,仅仅为一种逻辑功能划分,实际实现时可以有另外的划 分方式,又例如,多个单元或组件可以结合或者可以集成到另一个系统,或一些特征可以忽略,或不执行。另一点,所显示或讨论的相互之间的耦合或直接耦合或通信连接可以是通过一些通信接口,装置或单元的间接耦合或通信连接,可以是电性,机械或其它的形式。
所述作为分离部件说明的单元可以是或者也可以不是物理上分开的,作为单元显示的部件可以是或者也可以不是物理单元,即可以位于一个地方,或者也可以分布到多个网络单元上。可以根据实际的需要选择其中的部分或者全部单元来实现本实施例方案的目的。
另外,在本发明提供的实施例中的各功能单元可以集成在一个处理单元中,也可以是各个单元单独物理存在,也可以两个或两个以上单元集成在一个单元中。
所述功能如果以软件功能单元的形式实现并作为独立的产品销售或使用时,可以存储在一个计算机可读取存储介质中。基于这样的理解,本发明的技术方案本质上或者说对现有技术做出贡献的部分或者该技术方案的部分可以以软件产品的形式体现出来,该计算机软件产品存储在一个存储介质中,包括若干指令用以使得一台计算机设备(可以是个人计算机,服务器,或者网络设备等)执行本发明各个实施例所述方法的全部或部分步骤。而前述的存储介质包括:U盘、移动硬盘、只读存储器(ROM,Read-Only Memory)、随机存取存储器(RAM,Random Access Memory)、磁碟或者光盘等各种可以存储程序代码的介质。
应注意到:相似的标号和字母在下面的附图中表示类似项,因此,一旦某一项在一个附图中被定义,则在随后的附图中不需要对其进行进一步定义和解释,此外,术语“第一”、“第二”、“第三”等仅用于区分描述,而不能理解为指示或暗示相对重要性。
最后应说明的是:以上所述实施例,仅为本发明的具体实施方式,用以说明本发明的技术方案,而非对其限制,本发明的保护范围并不局限于此,尽管参照前述实施例对本发明进行了详细的说明,本领域的普通技术人员应当理解:任何熟悉本技术领域的技术人员在本发明揭露的技术范围内,其依然可以对前述实施例所记载的技术方案进行修改或可轻易想到变化,或者对其中部分技术特征进行等同替换;而这些修改、变化或者替换,并不使相应技术方案的本质脱离本发明实施例技术方案的精神和范围。都应涵盖在本发明的保护范围之内。因此,本发明的保护范围应所述以权利要求的保护范围为准。
- 还没有人留言评论。精彩留言会获得点赞!