一种基于网格搜索的支持向量机行程时间预测方法与流程

本发明涉及一种基于网格搜索的支持向量机行程时间预测方法，属于智能交通领域。该方法可以基于船舶自动识别系统(automaticidentificationsystem,ais)数据，实现对内河船舶行程时间的预测，为航务管理部门提供理论与技术支持。

背景技术：

内河航运是我国重要的运输方式之一，是综合利用水资源和复杂运输体系的重要参与成员，且连接着内陆区域与沿海区域，为我国每年带来巨大的经济利润。但是，我国内河航运依然存在有船舶航行安全、物流优化管理、港口规划调度等问题，直接影响内河航运的发展。近几年，内河沿岸ais基站建设飞速，装有ais的船舶数量快速增长，并且ais可以采集丰富的数据信息，进行多种应用。因此，可以对内河ais数据运用数据挖掘理论方法进行挖掘及分析，实现船舶行程时间的精准预测，以提高航务管理部门的管理水平，促进内河航运的迅猛发展。

行程时间预测算法在国内外均有了较为深入的研究，但现今其主要针对于城市道路行程时间的预测。同时，在国内外学者基于ais船舶交通数据进行的船舶行为研究中，已经在解决船舶碰撞以及船舶交通量、船舶运动模式、船舶航行轨迹、船舶间时距、船舶到达时间的预测方面有了很好的方法。但是，针对内河船舶行程时间预测方面还没有较为深入的研究，这一问题亟待解决。

技术实现要素：

本发明的目的为克服上述技术问题，提出一种基于网格搜索的支持向量机行程时间预测方法。本发明从城市道路行程时间的预测方法切入，选择适用于内河船舶航行方式的支持向量机(supportvectormachine,svm)算法，不仅弥补了现有针对内河船舶行程时间预测方面研究的不足，而且实现了实现上下行船舶划分等数据预处理工作。该方法预测效果较为精确、稳定，应用领域广泛。

本发明是一种基于网格搜索的支持向量机行程时间预测方法，包括以下几个步骤：

步骤一、基于ais数据，依照缺失数据的排查、上下行船舶的划分以及冗余数据的剔除三大步骤进行数据的预处理工作；

步骤二、构建基于历史时段的内河船舶行程时间预测模型，并根据模型得到训练数据集；

步骤三、基于svm网格搜索法寻找预测模型的最优参数；

步骤四、基于最优参数，实现对内河船舶行程时间的预测；

步骤五、预测结果评价。

本发明的优点在于：

(1)本发明突出的优点就是从城市道路行程时间的预测方法切入，通过svm算法自学习能力，捕获过去时段行程时间及多种随机影响因素与当前时段行程时间之间的复杂函数关系，实现基于ais数据的内河船舶行程时间预测。

(2)本发明创造性地使用ais数据，运用数据挖掘理论方法进行挖掘及分析，并实现了缺失数据的排查、上下行船舶的划分以及冗余数据的剔除等数据预处理工作；

(3)基于svm网格搜索法寻找预测模型的最优参数，并在最优参数下实现对内河船舶行程时间的预测，预测精度大幅提高。

附图说明

图1为本发明的方法流程示意图；

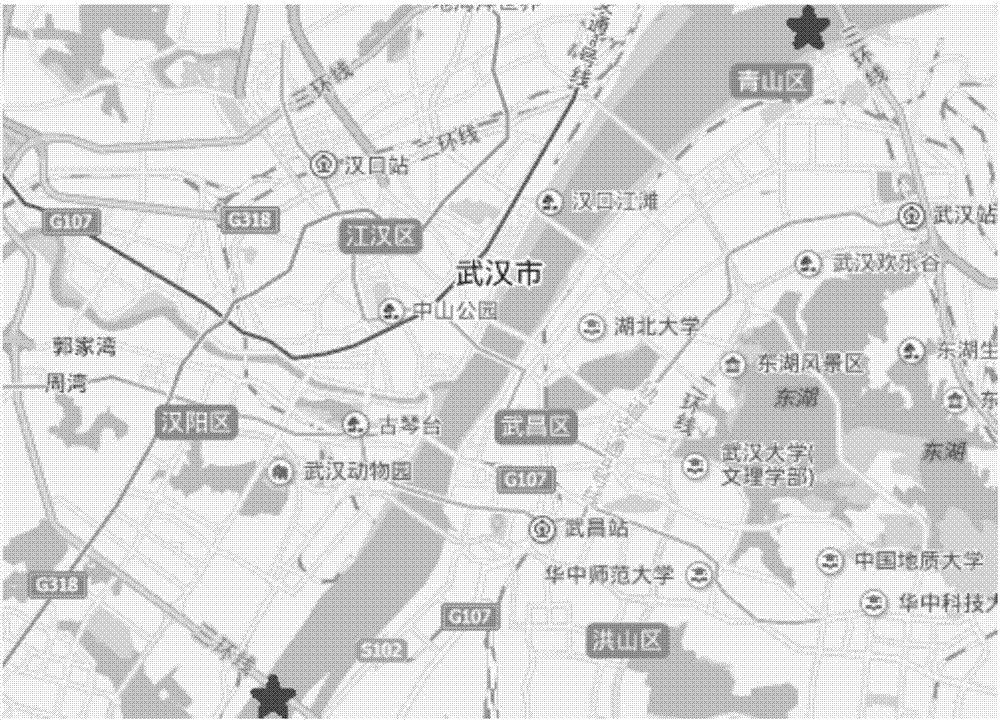
图2为实施例中所研究区域示意图；

图3为实施例中上下行船舶航向示意图；

图4为实施例中网格搜索法搜索结果示意图；

图5为实施例中预测值散点示意图；

图6为实施例中预测值与真实值对比示意图。

具体实施方式

下面将结合附图和实施例对本发明作进一步的详细说明。

本发明提出一种基于网格搜索的支持向量机行程时间预测方法，流程图如图1所示，包括如下步骤：

步骤一、ais数据预处理

1)、缺失数据的排查：采集到的ais数据主要包括mmsi号、归档时间、经度、纬度、对地航速、对地航向、船舶类型等信息。在原始数据中，某一时刻的某一船舶可能存在有上述信息不完整的情况，对于此类不完整信息，应该予以排查及去除。

2)、上下行船舶的划分：根据船舶对地航向角不同进行上下水的划分，将原始ais数据分为上行船舶及下行船舶两大部分。根据内河船舶航行特点可知，在内河上行驶的船舶，其航行速度会受到上下水不同的影响，下水船舶航行速度明显高于上水船舶，会对行程时间产生影响，进而在建立的预测模型中会产生不同的参数。根据船舶航行对地航向角的不同，将原始数据导入地图中，得到船舶上下行区分图，从而对上行船舶和下行船舶进行划分。

3)、冗余航段的剔除：在原始数据中，会出现例如船舶未行驶、经纬度数据错误、船舶位于长江航道以外等错误数据，除了剔除上述错误数据之外。有部分船舶位于支流航段，还有部分船舶为轮渡船，并未沿着内河的上下行方向航行，因此，上述类似船舶也应在原始数据中剔除。

步骤二、构建基于历史时段的内河船舶行程时间预测模型

1)、预测模型的构建：本发明利用svm的自学习能力，自我学习各项因素之间的复杂函数关系。内河船舶当前时段的行程时间与该时段的前几个时段的行程时间有着一定的函数关系，即：

tk＝f(tk-1,tk-2,...,tk-n)(1)

其中，tk代表在当前时段符合预测航段的各个船舶实际行程时间的平均值；tk-n代表预测时段k的前几个时段符合预测航段的各个内河船舶实际行程时间，n＝1，2，…，n。

在预测航段内选取定点a和定点b，a、b之间的航段l即为预测航段。其中，为保证每一组训练数据的起点及终点位置基本相同，需要做如下限定，即假设所选取的起点a的坐标为(x,y)，那么实际起点a’的坐标需要满足一定的精度要求，即:|x-x'|≤ε，|y-y'|≤ε。同理，终点b也需要满足以上精度要求。

2)、构建预测模型的训练数据集：在基于历史时段的预测模型中，因为越靠近当前时段的时段与预测时段的相关程度越大，因此训练集中的每组数据要包含适当数量时段的船舶行程时间，又因为船舶航行速度是影响内河船舶行程时间的又一个重要因素，因此要采用与内河船舶行程时间密切相关的历史时间序列及该时段各船舶航行的平均速度作为预测的特征值。首先将数据分为上行情景一和下行情景二两种情况，然后第一维输入向量为t1第二纬输入向量为t2，第三维输入向量为t3、第n维输入向量为tn，平均速度向量为v，输出向量为tn+1。之后，将构造的训练数据导入svm程序中，svm通过历史数据进行自我学习，找到输入值与输出值之间的复杂函数关系，即可实现对内河船舶行程时间的预测。

3)、模型参数的确定：本发明所建立的内河船舶行程时间预测模型选用高斯径向基核函数和ε-不敏感损失函数。其中σ为核参数，ε为不敏感损失函数参数。

σ表示在libsvm软件包中的参数gamma，反映了训练数据集的分布或范围特性，局部邻域宽度由它来决定；

ε表示在libsvm软件包中的参数epsilon控制着不敏感带的宽度，并会影响着对支持向量的个数。ε的值较小时，回归精度较高，支持向量数则较多，相反，ε的值较大时，回归精度较低，但支持向量数会变少；

c表示在libsvm软件包中的参数cost，同时也被称为正则化参数，它对达到误差上限的样本的惩罚程度进行控制，当取值增大时，样本的惩罚随之增大。

步骤三、基于svm网格搜索法寻找预测模型的最优参数

对于径向基核函数的参数c、σ、ε的选择，本发明采用网格搜索中的k折交叉验证法。k折交叉验证是将训练样本平均分成k份，每次拿出k-1份作为训练数据，剩下的一份作为测试数据，这样重复做k次，获得k次的平均交叉验证准确率作为结果，进行k折交叉验证之后会返回一个效率值，效率最大值所对应的cost和gamma参数就是径向基核函数的最优参数。在下一步使用svm函数的预测工作中，将上述参数的值定位寻优获得的最优值，即可达到相对较好的预测小效果。具体步骤如下：

1)、设定搜索范围：首先调用r统计软件的e1071函数包，选择所建立的训练数据集，设定输入及输出数据，并设定gamma参数cost参数的搜索范围后进行搜索，同时设定set.seed(10)来保证每次对训练集的划分及选取一致。

2)、最优值的判断：当经过搜索后所得到的gamma参数cost参数值为上下界的临界值时，此时搜索值不一定是最优值，需要重新设定搜索范围，获取新的参数值。

3)、获取最优值：经过上述几次搜索后，当搜索后得到的参数值介于上下界之间时，证明所设定的搜索范围正确，此时搜索到的参数值即为最优值。

步骤四、基于最优参数，实现对内河船舶行程时间的预测

1)、svm模型的建立：编写程序，在r中导入训练数据集，并设定好输入数据集合x，输出数据集合y。在调用svm函数时，需要设定svm支持向量机核函数的类型，以及gamma和cost的最优值

2)、训练数据的测试：在本步骤中，需要对训练数据进行测试，采用上述预测模型，对输入集合x预测，得到预测值，并与真实值进行对比。

3)、各因子权重的确定：本步骤中通过attr()函数确定对象属性，得出各因子权重。

步骤五、预测结果评价

1)、预测结果的可视化：在该步骤中，本发明以实际的观测值为横坐标，以所建立的svm模型产生的预测值作为纵坐标，绘制相关散点图来进行对比。为了便于比较，同时本发明建立一组观测值与预测值完全相同的情况，与上述散点图进行对比，可以更加直观的看出预测值的分布。

2)、评级指标计算：本发明选择了以下四种误差指标对其预测结果进行对比分析，其计算公式如下所示：

①平均绝对误差(mad)为：

②平均相对误差绝对值(mape)为：

③最大绝对误差(mae)为：

mae＝max|实际值-预测值|(4)

④最大相对误差(mre)为：

实施例

一种基于网格搜索的支持向量机行程时间预测方法，以长江武汉段的ais数据为例，具体如下：

步骤一、在原始数据中，监测航段范围为武汉市三环线以内部分，全长约22km，如图2标注所示，监测时间为2014年8月11日00:00:00到2014年8月19日13:59:59，共计监测时长206个小时。基于sqlserver2008，经排查后，共计产生167865条数据。

根据船舶航行对地航向角的不同，将上述原始数据导入，可得到如图3所示的船舶上下行区分图，其中红色代表上行船舶的航行路线，蓝色代表下行船舶的航行路线，将上述167865条数据划分为上行船舶及下行船舶。

如图3中编号为1、2的两个黑色长方形框内所示，其中黑色方框1表示长江支流航段，黑色方框3表示轮渡船舶。因此，上述两类船舶也应在原始数据中剔除。本文对上述已分类的上下行船舶分别进行多于数据的剔除工作。在上行船舶中，需剔除如图3中编号1及编号2中的两部分红色区域。依据百度地图坐标拾取系统的坐标显示，可以得出以下剔除数据的经纬度范围：黑色方框1为lon＜114.2955°且lat≥30.5661°；同理，黑色方框2为lon≥114.2979°且lat＜30.5715°，剔除两组数据后，上行船舶数据共计86589条。在下行船舶中，需剔除如图3中编号1中的蓝色区域。同样，依据百度地图坐标拾取系统的坐标显示值，剔除数据的经纬度范围黑色方框1为lon＜114.2978°且lat≥30.5660°，剔除以上一组数据后，下行船舶数据共计57586条。

步骤二、本实施例将2小时作为一个监测时段。监测时间为2014年8月11日00:00:00到2014年8月19日13:59:59，共计监测时长206个小时，因此可以划分为103个时间段。同时，为了保证在每个时段内都存在有船舶经过航段l，因此航段l的起始坐标a、b两点的确定至关重要。本文通过对各个时段的统一排查统计，最终确定监测航段为武汉市白沙洲大桥到武汉市晴川阁小学一段，即a点纬度值为30.4905°±0.005°，b点的纬度值为30.5654°±0.005°。

在构造svm算法程序可以识别的训练集时，本发明将行程时间统一换算为以秒为单位，若某一时间段内有多条船舶符合a、b两点的经纬度取值范围，此时需取这几条船舶的平均值作为该时段的船舶行程时间。训练数据集第一条数据是将时段1、2、3、4的行程时间作为输入，时段5的行程时间作为输出；第二条，将时段2、3、4、5的行程时间作为输入，时段6的行程时间作为输出；因此该训练数据集共计99条数据。

步骤三、本文设定k值为10来进行交叉验证，首先调用e1071函数包，选择所建立的训练数据集，设定输入及输出数据，并对gamma参数的搜索范围设定为2^-5～2^-1，cost参数的搜索范围设定为2^-2～2²，搜索结果如图4所示。

由运行结果可见gamma＝0.0625和cost＝0.5，搜索参数值均介于上临界值与下临界值之间。因此，此时达到了svm径向基函数的最优参数。即通过基于网格搜索法的svm参数优化，最终确定最优参数依次为c＝0.5、ε＝0.1、σ＝0.0625。

步骤四、编写程序，在r中导入训练数据集，并设定好输入数据集合x，输出数据集合y。在调用svm函数时，需要设定svm支持向量机核函数的类型为径向基核函数“radial”，gamma值为0.0625，cost值为0.5。从运行结果可知，svm函数的工作方向为eps-回归，epsilon的值为0.1，支持向量个数为87。

步骤五、采用上述预测模型，对输入集合x预测，得到预测值，并与真实值进行对比，以所建立的svm模型产生的预测值作为纵坐标进行对比，结果显示如图5所示。为了便于比较，同时本文建立一组观测值与预测值完全相同的情况，如图6所示。从结果可以看出，预测结果有较明显的趋近观测值的趋势，且观测值两边的散点分布均匀。由于训练数据数据集只有99组，导致一些预测结果偏差较大，如果增大训练数据至200组以上，结果将会有明显改观。

步骤五：分别计算平均绝对误差(mad)、平均相对误差绝对值(mape)、最大绝对误差(mae)、最大相对误差(mre)，各个指标计算结果如表1所示，单位(秒)。

表1评价指标结果

以上详细描述了本发明的优选实施案例，但是本发明并不局限于上述实施案例的具体细节，在本发明的整体结构范围内，可以对本发明的部分步骤进行多种变换并重新组合，本发明对各种可能的组合方式不再列举，这些变换组合均属于本发明的保护范围。