1.本发明属于智能交通与机器学习信息安全的交叉领域,涉及基于快速梯度下降(fgsm)的单交叉口信号控制的交通状态对抗扰动生成方法。
背景技术:2.交通拥堵问题已成为城市交通面临的迫切挑战,设计现代城市时,最关键的考虑因素之一就是开发智能交通管理系统。交通管理系统的主要目标是减少交通拥堵,如今这已成为大城市的主要问题之一。高效的城市交通管理可节省时间和金钱,并减少向大气排放的二氧化碳。
3.强化学习(rl)作为交通信号控制问题的一种机器学习技术,已经产生了令人印象深刻的结果。强化学习不需要事先对环境有全面的了解,例如交通流量。相反,他们通过与环境进行交互能够获取知识并为环境动力学建模。在环境中执行每个操作后,它将获得标量奖励。所获得的报酬取决于采取的行动的程度,而智能体的目标是学习最佳控制策略,因此通过与环境的反复交互,可以使折价的累积报酬最大化。深度强化学习(drl)由于具有快速适应周围环境的出色能力,因此在现实世界中具有众多应用。尽管drl具有很大的优势,但它容易受到对抗性攻击,例如:引诱攻击、策略定时攻击、基于值函数的对抗攻击、木马攻击等。
技术实现要素:4.为了克服已有技术的不足,本发明提供了基于快速梯度下降的单交叉口信号控制的交通状态对抗扰动生成方法,可以对车辆数量及其所处位置添加少量扰动且保证扰动具有实际物理意义,从而高效地生成对抗扰动,大幅降低模型的性能和交通路口流畅程度。
5.本发明解决其技术问题所采用的技术方案是:
6.一种基于快速梯度下降的单交叉口信号控制的交通状态对抗扰动生成方法,包括以下步骤:
7.步骤1:在单交叉口道路网格上训练强化学习deep q network(dqn)智能体模型,训练完成后模型的网络参数不再发生变化,且具有较高的迁移性,在单交叉口测试过程中体现出高流畅度且无拥堵发生;
8.步骤2:在交通路口获取各个路口输入端的车辆数量及其所处位置即输入,将当前车辆数与位置输入到模型中,会生成对应的交通信号灯即输出动作,利用fgsm攻击算法,对各个时刻的输入逐一进行攻击,得到相应的对抗扰动;
9.步骤3:对生成的对抗扰动进行离散化处理,再将生成的对抗扰动与原始采集到的交通流量相结合得到最终的扰动状态即此时输入到模型中去的交通路口车辆数量及其位置;
10.步骤4:在当前构建的扰动状态中,对扰动的大小进行限制,当扰动量小于扰动限
制时将扰动状态输入模型中;当扰动量大于扰动限制时将原始状态输入模型;
11.步骤5:对生成的对抗扰动进行性能的测试,将状态输入模型后,智能体会根据当前状态选取交通信号灯的相位,来控制单交叉口的车流量,最后在sumo上对不同输入状态的交通流量得到的红绿灯相位对交通路口的流畅度进行对比。
12.作为人工智能领域的研究热点,深度强化学习(drl)在机器人控制,计算机视觉,智能交通等各个领域都取得了一定的成功。同时,其遭到攻击的可能性以及它是否具有强大的抵抗能力也成为近年来的热门话题。因此,本发明在深度强化学习中选择了具有代表性的deep q network(dqn)算法,将单交叉口信号灯控制作为应用场景,并采用快速梯度下降法(fgsm)攻击dqn算法以生成对抗样本。
13.本发明的技术构思为:根据已有的强化学习dqn算法训练的交通路口信号灯控制模型,利用基于fgsm攻击并结合梯度值大小对对抗扰动进行离散化处理生成对抗样本,将对抗扰动与原始状态相结合得到最终的扰动状态输入到智能体模型中,最后在sumo上对单交叉路口的流畅或拥堵程度检验效果。
14.本发明的有益效果主要表现在:利用fgsm攻击算法对梯度最大值生成相应对抗扰动且生成的扰动均为离散值,将对抗扰动与原始交通流量结合形成扰动状态,且对扰动状态的扰动量添加扰动限制,该输出即为扰动状态。本发明可以在使输出的扰动具有物理意义的情况下限制扰动的大小,从而高效的生成对抗状态,增加路口的排队长度和等待时间,大幅降低模型的性能,使交通路口流通度大大降低。
附图说明
15.图1是强化学习示意图。
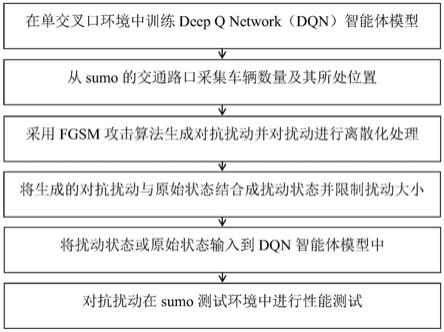
16.图2是fgsm生成对抗扰动的总体流程图。
17.图3是单交叉口示意图。
18.图4是车辆位置的离散状态。
19.图5是单交叉口车辆等待队列长度对比图。
20.图6是单交叉口车辆等待时间对比图。
具体实施方式
21.下面结合附图对本发明作进一步描述。
22.参照图1~图6,一种基于快速梯度下降的单交叉口信号控制的交通状态对抗扰动生成方法,包括以下步骤:
23.步骤1:强化学习是一种和环境进行不断交互的算法,如图1所示。强化学习算法包含三个最基本的要素:环境状态、智能体动作、环境奖励。以典型十字交叉路口为例。首先在单交叉口道路网格上训练强化学习智能体模型,对进入单交叉口的所有道路上的交通状态进行离散编码。将单交叉口从路段入口到停车线之间长度为l的道路k(k=1,2,3,4)等距离划分为c个离散单元,将t时刻单交叉口的道路k的车辆位置表示为车辆位置矩阵s
k
(t),当车辆头部位于某个离散单元上时,则车辆位置矩阵s
k
(t)对应第i(i=1,2,
…
,c)个位置的值为0.5,否则值为
‑
0.5,公式表示为:
[0024][0025]
其中表示车辆位置矩阵s
k
(t)第i个位置的值,将t时刻四个路口输入端的车辆位置矩阵s
k
(t)按行首尾拼接构成s
t
,公式表示为:
[0026]
s
t
=[s1(t),s2(t),s3(t),s4(t)]
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(2)
[0027]
再把s
t
作为环境状态输入到智能体模型中训练,智能体输出相应的动作即红绿灯将要执行的相位(如南北绿灯或东西绿灯)。
[0028]
以典型十字交叉路口为例进行说明。我们定义交通灯的相位作为动作空间a={a1,a2,a3,a4},其中a1为东西方向绿灯,a2为东西方向左转绿灯,a3为南北方向绿灯,a4为南北方向左转绿灯。在运行时设a
i
的相位的初始时长为m,黄灯相位时长为n。在t时刻将当前状态s
t
输入到智能交通灯模型中,智能交通灯选择相位a
i
(i=1,2,3,4),当a
i
相位执行完后,智能交通灯从环境中采集t+1时刻的状态s
t+1
,然后选择相位a
j
(j=1,2,3,4)。若a
i
≠a
j
则a
i
相位执行时间不再延长,即a
i
相位结束,在a
i
相位结束后智能交通灯执行黄灯相位,在黄灯相位结束后,执行a
j
相位;若a
i
=a
j
,则a
i
相位执行时间延长m;将奖励r
t
设置为两个连续动作之间路口车辆的等待时间之差,公式表示为:
[0029]
r
t
=w
t
‑
w
t+1
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(3)
[0030]
其中w
t
,w
t+1
分别为t时刻和t+1时刻的进入单交叉口所有车道的等待时间。根据执行的动作再按照环境奖励对动作进行评判,从而不断更新网络的参数。所使用的强化学习模型为:deep q network(dqn)。结构包含卷积层、全连接层;参数包含卷积核大小、全连接层神经元的数量。用一个深度神经网络作为q值网络,,初始化网络参数,网络的输出就是q值,隐含层采用relu非线性激活函数,其中输出层的神经元个数与单交叉口的动作空间大小相等。公式表示为:
[0031]
q=h(ws
t
+b)
ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(4)
[0032]
其中w代表神经网络的权重,s
t
为网络的输入,b为偏置,h(.)表示relu激活函数。dqn的损失函数为:
[0033][0034]
l
t
=(y
t
‑
q(s
t
,a
i
;θ
′
))2ꢀꢀꢀꢀꢀꢀꢀꢀꢀꢀ
(6)
[0035]
其中y
t
代表目标值,a
i
,a
j
∈a表示智能体输出的动作即红绿灯相位,r
t
代表t时刻的奖励,γ为学习率,θ和θ
′
分别代表dqn中目标网络的参数w、b和估计网络的参数w’、b’,估计网络的参数是随着时间步长逐步更新的,目标网络的参数更新是每隔时间t从估计网络直接复制网络的参数,公式表示为:
[0036][0037][0038]
步骤2:在交通路口获取各个路口输入端的车辆数量及其所处位置即输入当前车
辆数与位置输入到模型中,会生成对应的交通信号灯即输出动作。利用fgsm攻击算法,对各个时刻的输入逐一进行攻击,得到相应的对抗扰动;过程如下:
[0039]
2.1:获取t时刻输入模型的输入值s
t
,其中s
t
代表t时刻从sumo获取的单交叉口输入端车辆数量及其所处位置;
[0040]
2.2:输入原始状态s
t
,经过已经训练好的dqn智能体模型,选择出动作值函数q最大的动作a
m
(m=1,2,3,4)即此时最优的红绿灯相位,公式表示为:
[0041][0042]
其中θ代表训练好的智能体模型网络的参数,a
m
表示输出的动作即红绿灯将要执行的相位。
[0043]
2.3:采用fgsm攻击算法,沿着梯度方向并根据符号函数进行赋值生成t时刻相对应的对抗扰动η
t
,公式表示为:
[0044][0045]
其中ε代表扰动系数,s
t
代表输入值即车辆所处位置,a
m
代表此时红绿灯执行的最优相位,sign代表符号函数,l
t
(θ,s
t
,a
m
)代表t时刻模型的损失函数。
[0046]
步骤3:由于所取状态是车辆数量及其位置,故为离散值。因此要对对抗扰动η进行处理,得到具有实际物理意义的扰动值。过程如下:
[0047]
3.1:其中c为交通路口输入端划分的离散单元数量,代表t时刻第i个离散单元的对抗状态。计算出t时刻的对抗扰动η
t
后,对t时刻的扰动取绝对值并找出其中最大值和最小值并按照大小顺序对η进行排序得到新的排序数组最后通过对扰动进行离散化处理,使其具有实际物理意义。
[0048]
3.2:在η
t
′
中按顺序读取扰动并与原始数据进行比较,若原始状态与对抗扰动不一致,则将对应扰动赋给对应的原始状态;若原始状态与对抗扰动是一致的,则再取η
t
′
中下一个对抗扰动按上述方式赋值,直到所选的扰动是有效的,最终得到扰动状态s
t
′
。
[0049]
步骤4:在当前构建的扰动状态中,对扰动的大小进行限制,当t时刻扰动量μ
t
≤δ(δ为扰动限制)时将扰动状态输入模型中;当扰动量μ
t
≤δ时将原始状态输入模型;
[0050]
计算t时刻扰动状态添加的扰动量μ
t
,公式表示为:
[0051][0052]
其中len(.)表示计算s
t
和s
t
′
中车辆状态为0.5的个数,当扰动量μ
t
≤δ时,将扰动状态s
t
′
输入智能体模型中,否则将原始状态s
t
输入到智能体模型中。
[0053]
步骤5:对生成的对抗扰动进行性能的测试,将状态输入模型后,智能体会根据当
前状态选取交通信号灯的相位,来控制单交叉口的车流量。最后在sumo上对不同输入状态的交通流量得到的红绿灯相位对交通路口的流畅度进行对比;
[0054]
所述步骤5的过程如下:
[0055]
5.1:各个时刻的原始状态s
t
输入到模型中模型会选择最优动作(红绿灯相位)控制路口车流量,并计算出交通路口的等待时间之差(奖励r
t
=w
t
‑
w
t+1
)。
[0056]
5.2:对添加有效扰动后的最终扰动s
t
′
计算扰动量μ
t
,对满足要求(μ
t
≤δ)的输入状态输入到智能体模型中输出动作即红绿灯相位,此时同样计算交通路口的等待时间之差(奖励r
t
=w
t
‑
w
t+1
)。
[0057]
实例:实际实验中的数据,过程如下:
[0058]
(1)选取实验数据
[0059]
实验数据是由sumo上的单交叉路口随机生成的100辆汽车,每辆汽车大小、生成位置距离交叉路口的距离和汽车从生成到通过路口的速度都是相同的。交通路口红绿灯相位的初始时间是绿灯10秒,黄灯4秒。从停车线开始长度为700米的道路k(k=1,2,3,4)划分为长度为7米的100个离散单元。交通路口输入端采集到的原始状态s
t
用来记录单交叉口输入端车辆的数量以及所处位置。扰动限制δ=20%。
[0060]
(2)实验结果
[0061]
在结果分析中,我们使用了单交叉路口作为实验场景,训练了强化学习deep q network(dqn)智能体模型,采用快速梯度下降法(fgsm)并对扰动进行离散化处理生成对抗扰动,对交叉路口输入端的车辆数量及其位置进行改变从而造成红绿灯相位的改变,在有攻击和无攻击两种情况下进行了对比实验,实验结果如图5,图6所示(在不断进行攻击时,红绿灯相位不能很好的保证单交叉口车辆流通导致车辆堆积在路口处。但当堆积的车辆足够多时,此时需要增加很大的扰动才能攻击成功,故此时扰动超过扰动限制则将原始状态输入到智能体模型中,此时路口车辆就能快速流通起来,从而使得等待时间和等待车辆会有大幅的下降)。
[0062]
本说明书的实施例所述的内容仅仅是对发明构思的实现形式的列举,仅作说明用途。本发明的保护范围不应当被视为仅限于本实施例所陈述的具体形式,本发明的保护范围也及于本领域的普通技术人员根据本发明构思所能想到的等同技术手段。
