质子交换膜燃料电池内部水分布预测方法与流程

本发明属于电化学燃料电池领域，具体涉及一种用于对燃料电池的性能进行预测计算的方法。

背景技术：

质子交换膜燃料电池(pemfc)是一种将燃料中的化学能直接转化为电能的电化学反应动力装置，具有零排放和高功率密度等优点，并被广泛认为是将来最有可能取代内燃机作为汽车动力源的动力机械。但是，目前质子交换膜燃料电池性能及寿命还存在很大的提升空间，其中水管理的优劣是影响其性能的关键因素之一。

之所以要对质子交换膜燃料电池进行水管理，是因其质子交换膜需要保持一定的水含量才能保持高性能，同时，由于质子交换膜燃料电池水仅在阴极产生，特定工况下(如：高电流密度)又有可能发生“水淹”现象，这样就会降低燃料电池性能。因此，通过燃料电池内部结构优化设计等方法保持内部动态水平衡是提升燃料电池性能及寿命的一个关键因素。

建模仿真是获取质子交换膜燃料电池内部水分布的一条重要途径，不仅可节约大量的实验成本，还可预测通过实验手段很难观测到的燃料电池实际工作时的实时水分布情况。然而，由于质子交换膜燃料电池各组成部件以及水在不同部件中存在形态的不同，一般很难同时获得电池内部整体水分布情况。目前常见的燃料电池内部水分布研究大多将燃料电池分为膜电极(其中又包括：气体扩散层(gdl)、微孔层(mpl)、催化层(cl)和质子交换膜(membrane))和流道两部分，或忽略流道内液态水存在对膜电极水分布的影响，或仅研究流道内气液两相流动对燃料电池排水的影响，显然这两种研究方法均有其局限性，不能准确反映出质子交换膜燃料电池在特定工况下内部整体水分布情况。

本发明将提出一种基于数值计算的方法，对质子交换膜燃料电池内部电化学反应及导电过程、气液两相流动、膜吸放水和传热过程等进行综合分析，从而预测燃料电池内部水分布。

技术实现要素：

本发明的目的是提供一种质子交换膜燃料电池内部水分布预测方法，用于对质子交换膜燃料电池内部电化学反应及导电过程、气液两相流动、膜吸放水和传热过程等进行综合分析，从而预测燃料电池内部水的分布。

质子交换膜燃料电池内部水分布预测方法，用于构建三维数值模型进行求解计算，所述方法包括5个步骤：

(1)构建计算质子交换膜及催化层中，膜态水λ分布情况的守恒方程

其中：ρmem为质子交换膜干态密度，ew为当量质量；ω为nafion电解质体积分数；f为法拉第常数；jm为矢量离子电流密度；为有效扩散系数；smw为源项，由膜态水和液态水之间相变sd-l和质子交换膜两侧压力不同导致的渗透sp两部分组成。smw的具体表达式为：

(2)构建计算气体扩散层、微孔层及催化层中水分布情况的守恒方程

(2.1)通过构建液压pl和气压pg守恒方程来获得毛细压力pc，然后根据leverett方程提供的多孔介质中毛细压力与液态水体积分数s的关系式获得气体扩散层、微孔层及催化层中液态水分布情况，在此过程中，考虑气体扩散层纤维束平面方向和垂直纤维束平面方向的各向异性。

液压和气压守恒方程分别为：

其中下标l和g分别代表液态水和气体；ε表示孔隙率；k表示固有渗透率；计算时，k表示相对渗透率，m表示源项，液态水和气体源项的表达式分别为：

其中sv-l表示气态水和液态水之间的相变，ja和jc分别表示阳极和阴极催化层内单位体积的电化学反应速率。ja和jc由butler-volmer方程计算得到：

其中和分别表示阳极和阴极标准状态下的参考反应速率；t为温度；和分别表示氢气和氧气摩尔浓度，上标ref表示参考值。αa和αc分别表示阳极和阴极电化学反应的转移系数；r为通用气体常数；ηact表示活化过电势；该电势由催化层中电子电势和离子电势计算得出。电子电势和离子电势的守恒方程分别为：

其中和分别代表有效电子电导率和有效离子电导率，se和sion代表源项。

获得气压和液压分布后，根据leverett方程，可求得气体扩散层、微孔层和催化层中液态水分布：

pc＝pg-pl2-10

其中σ为表面张力系数；θ为多孔介质接触角；求解过程中，根据液压流量在两个平面内的不同平均固有渗透率，从而获得液态水体积分数分布：

其中kin表示气体扩散层纤维束平面内固有渗透率；kthrough则表示垂直纤维束平面内的固有渗透率。

(2.2)通过构建气体组分守恒方程，获得气体扩散层、微孔层和催化层中水蒸气分布：

其中ci表示气体摩尔浓度；表示气体有效扩散系数；si表示源项，下标i表示氢气、氧气和水蒸气。

(3)求解质子交换膜燃料电池流道内液态水分布，同时，气相内部求解组分守恒方程获得水蒸气分布。

(3.1)采用vof模型中质量守恒方程和动量守恒方程分别为：

其中：ρ表示密度；v表示速度矢量；g表示重力加速度常数；s表示质量源项，fs表示由表面张力引起的源项。

流道内的壁面吸附作用通过改变边界处的曲率实现：

其中和分别表示壁面垂直方向和切线方向的单位向量。

然后构建液相体积分数守恒方程获得流道内液态水分布：

αg+αl＝13-5

其中αg和αl分别表示气相和液相体积分数，sl表示液相源项。

(3.2)构建气相中气体组分守恒方程获得流道内水蒸气分布：

求解过程中，气相入口边界定义为质量入口边界，出口边界定义为压力出口且出口压力恒定为一个大气压。阴阳极入口气体质量流量ma和mc分别为：

其中

其中

式中ξ^a和ξ^c分别表示阳极和阴极进气化学计量比；i^ref表示参考电流密度；和分别表示阳极和阴极入口面积；和分别表示阳极和阴极活化面积；和分别表示阳极和阴极入口压力；rha和rhc分别表示阳极和阴极进气相对湿度。

(4)定义流道与气体扩散层交界面两侧质量守恒

在气体扩散层与流道接触面两侧定义气压、液压及气体浓度的数据交换，实现流道与气体扩散层气液两相的质量守恒。具体为将流道中获得的气压、根据气压和液相体积分数获得的液压和气体摩尔浓度赋值到气体扩散层一侧，而将气体扩散层中得到的通量转换为源项赋值到流道一侧进行计算。计算方程为：

通量f需等效为流道与气体扩散层接触面附近厚度为δ的区域内的源项：

其中s为式3-1中气液两相质量源项，sl为式3-4中液相源项。

(5)在整体计算域内构建能量守恒方程，获得温度分布：

其中cp,g和cp,l分别表示气相和液相的比热容；u表示速度；k^eff表示有效导热系数；st为源项。计算过程中，设置计算域边界温度为恒定值。

根据步骤(1)～(5)构建的守恒方程，建立三维数值模型进行求解计算，可最终获得设定工况下质子交换膜燃料电池流道、气体扩散层、微孔层和催化层中气态水和液态水分布以及质子交换膜和催化层中膜态水分布。

本发明所提出的对单个质子交换膜燃料电池内部水分布进行整体求解的方法，流道内采用气液两相流模型(vof)进行求解，将表面张力和壁面吸附的影响考虑在内。在气体扩散层(gdl)、微孔层(mpl)和催化层(cl)中，采用均匀多孔介质假设，以液压、气压为求解变量，基于leverett方程求解液态水体积分数。在此过程中，将gdl纤维束平面内和垂直纤维束平面内的各向异性考虑在内。在质子交换膜及催化层内部，求解膜态水守恒方程。在催化层内部定义膜态水与液态水或气态水的相变过程保证燃料电池内部整体水质量守恒，同时在gdl和流道接触面两侧定义一定形式的数据交换来保证气液两相的质量守恒。

本发明的特点以及带来的有益效果是：

(1)利用现有两相流模型对质子交换膜燃料电池流道内的气液两相流动进行模拟计算，考虑表面张力和壁面吸附作用，并通过特定方法将其与膜电极(气体扩散层、微孔层、催化层及质子交换膜)内的气液两相流动进行结合，提供了一种通过数值计算预测给定工况下单个质子交换膜燃料电池内部整体水分布的方法。

(2)将质子交换膜和催化层中存在的膜态水电渗拖拽作用采用对流项形式计算，更加符合实际情况。

(3)对于气体扩散层、微孔层和催化层中液态水体积分数的求解先液压和气压方程然后基于leverett方程计算的方式获得，充分反映了液态水在不同多孔介质界面处存在的突变现象；并且提出了在气体扩散层中考虑固有渗透率各向异性时，用于计算液态水体积分数的平均固有渗透率的计算公式。

(4)流道入口质量边界条件下，计算氢气和氧气浓度时，入口压力在计算过程中根据流道内流动情况实时更新，而不是假设为一个大气压(传统做法)，更能准确反映质子交换膜燃料电池流道内流动情况。

附图说明

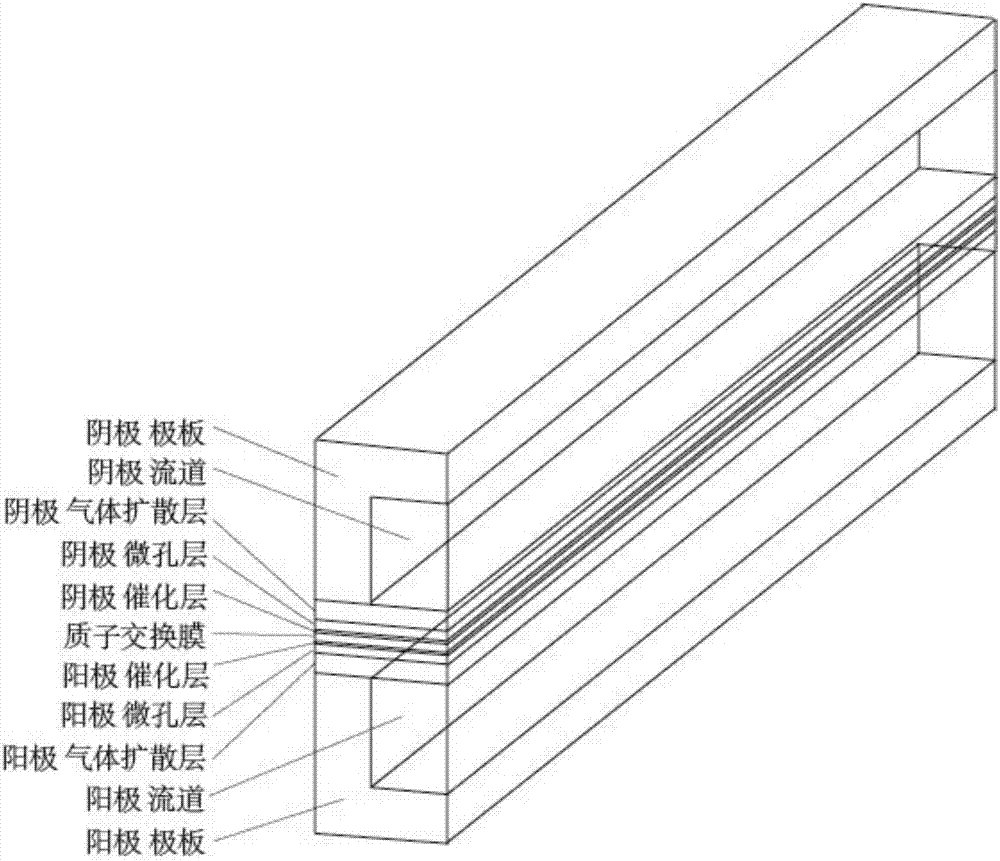
图1质子交换膜燃料电池流道与mea气压、液压及气体浓度数据交换示意图。

图2质子交换膜燃料电池计算域。

图3表示质子交换膜及催化层中膜态水含量分布。

图4表示气体扩散层、微孔层及催化层中液态水体积分数分布情况。

图5表示流道中液态水体积分数分布情况。

具体实施方式

以下通过具体实施例对本发明的方法步骤过程作进一步的说明，需要说明的是本实施例是叙述性的，而不是限定性的，不以此限定本发明的保护范围。

质子交换膜燃料电池内部水分布预测方法，用于构建三维数值模型进行求解计算，具体方法通过5个步骤予以实现：

(1)构建计算质子交换膜及催化层中，膜态水λ分布情况的守恒方程

质子交换膜(主要成分为nafion电解质)在燃料电池工作过程中会吸收一定量的水来保持较高的离子传导率，以这种形态存在的水称为膜态水，同时催化层中也存在一定含量的nafion电解质，所以膜态水λ的求解区域包括质子交换膜(membrane)和催化层两部分。其守恒方程为：

不同于之前的膜态水守恒方程，该方程中对电渗拖拽作用采用与实际更加相符的对流项进行计算。式中：ρmem(kgm^-3)为质子交换膜干态密度，ew(kgmol^-1)为当量质量；ω为nafion电解质体积分数(质子交换膜中为1)；f为法拉第常数96487cmol^-1；jm(am^-2)为矢量离子电流密度；为有效扩散系数；smw(molm^-3s^-1)为源项，由膜态水和液态水之间相变源项sd-l和质子交换膜两侧阴阳极催化层之间由压力差引起的源项sp两部分组成。smw的具体表达式为：

(2)构建计算气体扩散层、微孔层及催化层中水分布情况的守恒方程

(2.1)通过构建液压pl和气压pg守恒方程来获得毛细压力pc。在本发明中，将质子交换膜燃料电池中的气体扩散层、微孔层及催化层均视为均匀多孔介质。由于液态水体积分数在不同多孔介质交界面处存在突变现象，选择先求解液压方程和气压方程，然后根据leverett方程提供的多孔介质中毛细压力与液态水体积分数s的关系式获得其内部液态水分布。同时考虑气体扩散层纤维束平面方向和垂直纤维束平面方向的各向异性，微孔层和催化层则认为是各向同性。

液压和气压守恒方程分别为：

其中下标l和g分别代表液态水和气体；ε表示孔隙率；ρ(kgm^-3)表示密度，k(m²)表示固有渗透率；k表示相对渗透率，μ(kgm^-1s^-1)表示动力粘度，p(pa)表示压力，m(kgm^-3s^-1)表示源项，液态水和气体的表达式分别为：

其中sv-l表示气态水和液态水之间的相变，mh2、mo2和mh2o(kgmol^-1)分别表示氢气、氧气和水的摩尔质量，ja和jc分别表示阳极和阴极催化层内单位体积的电化学反应速率，ja和jc由butler-volmer方程计算得到：

其中和上标分别表示阳极和阴极标准状态下的参考反应速率；t(k)为温度；和分别表示氢气和氧气摩尔浓度，上标ref表示参考值；αa和αc分别表示阳极和阴极电化学反应的转移系数；r为通用气体常数8.314jmol^-1k^-1；ηact(v)表示活化过电势；该电势由催化层中电子电势和离子电势计算得出，电子电势和离子电势的守恒方程分别为：

其中电子电势守恒方程计算域为极板、气体扩散层、微孔层和催化层，离子守恒电势计算域为催化层和质子交换膜。和分别代表有效电子电导率和有效离子电导率。在气体扩散层内考虑有效电导率在纤维束平面和垂直纤维束平面有效电子电导率的各向异性，se和sion(am^-3)代表源项，分别为。

求解电子电势时，在阳极极板表面定义总体过电势ηtotal(v)，即可逆电势er与输出电压vout之间差值，在阴极极板表面定义参考电势0v。

ηtotal＝er-vout

获得气压和液压分布后，根据leverett方程，可求得气体扩散层、微孔层和催化层中液态水分布：

pc＝pg-pl2-10

其中σ(nm^-1)为表面张力系数；θ为多孔介质接触角。由于气体扩散层纤维束平面内和垂直纤维束平面内固有渗透率的不同，在求解s时根据液压流量在两个平面内的不同计算平均固有渗透率。

在气体扩散层内计算气压和液压分布时，考虑固有渗透率在纤维束平面(in-plane)和垂直纤维束平面(through-plane)内的各向异性，表达式为：

其中kin表示气体扩散层纤维束平面内固有渗透率；kthrough则表示垂直纤维束平面内的固有渗透率。

(2.2)通过构建气体组分守恒方程，建立气体扩撒层、微孔层和催化层中氢气、氧气和水蒸气守恒方程：

其中ci(molm^-3)表示气体摩尔浓度；表示气体有效扩散系数；计算过程中考虑其在气体扩散层中纤维束平面和垂直纤维束平面各向异性，si(molm^-3s^-1)表示源项，下标i表示氢气、氧气和水蒸气。

(3)采用vof两相流模型求解获得质子交换膜燃料电池流道内液态水分布。求解过程中，将表面张力和流道壁面吸附作用考虑在内，同时求解气相内组分守恒方程获得流道内反应气体及水蒸气分布。

(3.1)vof模型中质量守恒方程和动量守恒方程分别为：

其中：ρ表示密度；v(ms^-1)表示速度矢量；g表示重力加速度常数9.8ms^-2；s(kgm^-3s^-1)表示质量源项，fs表示由表面张力引起的源项。

其中：i表示单位矩阵，流道内的壁面吸附作用通过改变边界处的曲率实现；和分别表示壁面垂直方向和切线方向的单位向量。

流道内的壁面吸附作用通过改变边界处的曲率实现：

然后构建液相体积分数守恒方程获得流道内液态水分布：

αg+αl＝13-5

其中αg和αl分别表示气相和液相体积分数，sl(kgm^-3s^-1)表示液相源项，

(3.2)构建气相中气体组分守恒方程获得流道内水蒸气分布：

气相气体组分守恒方程为：

求解过程中，气相入口边界定义为质量入口边界，出口边界定义为压力出口且出口压力恒定为一个大气压，阴阳极入口气体质量流量ma和mc分别为：

其中

其中

式中ξ^a和ξ^c分别表示阳极和阴极进气化学计量比；i^ref(am^-2)表示参考电流密度；和分别表示阳极和阴极入口面积；和分别表示阳极和阴极活化面积；和分别表示阳极和阴极入口压力(在计算过程中根据流道内流动情况实时更新)；rha和rhc分别表示阳极和阴极进气相对湿度，

(4)定义流道与气体扩散层交界面两侧质量守恒

由于电极和流道内气液两相分布求解方式的不同，为同时获得质子交换膜燃料电池一定工作条件下的水分布情况，需要保证流道与气体扩散层气液两相的质量守恒。本实施例通过在气体扩散层与流道接触面两侧定义气压、液压及气体浓度的数据交换实现：具体做法为将流道一侧的气体压力、液体压力(通过气体压力与流道内液相体积分数经leverett方程计算得到)和各气体组分浓度赋值到气体扩散层一侧作为边界条件，然后将气体扩散层侧的通量f(包括对流动量和扩散通量两部分)返回流道一侧，具体如附图1所示。计算方程为：

数据交换过程中，气体扩散层一侧求解得到的通量f需等效为气体扩散层与流道交界面附近(流道一侧)厚度为δ的区域内的源项进行计算：

(5)在整体计算域内构建能量守恒方程，获得温度分布：

在质子交换膜燃料电池工作过程中，会不断产生热量，导致各部分温度分布并不相同，而上述计算过程中很多参数与温度有关。因此，本发明在整体计算域内求解能量守恒方程以获得温度分布：

其中cp,g和cp,l(jkg^-1k^-1)分别表示气相和液相的比热容；u(ms^-1)表示速度；k^eff(wm^-1k^-1)表示有效导热系数。计算时考虑其在气体扩散层中纤维束平面内和垂直纤维束平面内的各向异性。在此过程中，计算域边界温度均设置为恒定值。st(wm^-3)为源项，表达式如下所示：

其中δsa和δsc(jmol^-1k^-1)分别为阳极和阴极电化学反应熵变，h(jmol^-1)为水相变过程中潜热值。

根据步骤(1)～(5)构建的守恒方程，建立三维数值模型进行求解计算，可最终获得设定工况下质子交换膜燃料电池流道、气体扩散层、微孔层和催化层中气态水和液态水分布以及质子交换膜和催化层中膜态水分布。

具体计算实施例

计算给定输出电压、进气加湿程度等工况下质子交换膜燃料电池内部水分布时，首先需要构建计算域，包括阴阳极极板(bp)、流道(channel)、气体扩散层、微孔层、催化层以及质子交换膜，如附图2所示。选取流道出入口截面宽0.8×10^-3m，高1.0×10^-3m，极板总高度和总宽度均为1.5×10^-3m，gdl和mpl厚度分别为1.9×10^-4和2.0×10^-5m，阳极和阴极催化层厚度分别为5.0×10^-6和1.0×10^-5m，计算域总长0.01m，活化面积1.5×10^-5m²。

质子交换膜及催化层中膜态水计算：

本发明选用nafion212质子交换膜，厚度为5.08×10^-5m，干态密度ρmem＝1980kgm^-3,当量质量ew＝1.1kgmol^-1，膜渗透率kmem＝2.0×10^-20m²，催化层中电解质含量ω＝0.21。

利用bruggemann公式对膜态水扩散系数进行修正，修正系数为1.5：

膜态水与液态水相变源项sd-l(kgm^-3s^-1)表达式如下所示：

式中γd-l(s^-1)表示相变率，λeq表示平衡状态下的膜态水含量，表达式如下：

其中a表示水活度：

psat(pa)为水蒸气饱和蒸气压，是温度的单值函数：

阴阳极催化层中因压差引起的源项sp(kgm^-3s^-1)表达式为：

其中：和分别为阳极和阴极催化层平均液压，μl(kgm^-1s^-1)为液态水动力粘度，δmem和δcl(m)分别为膜和催化层厚度。

气体扩散层、微孔层和催化层：

气体扩散层、微孔层和催化层孔隙率ε依次为0.7、0.5和0.3，接触角θ依次为120°、120°、100°，固有渗透率k依次为1.0×10^-12、1.0×10^-12、1.0×10^-13m²，表面张力系数σ＝0.625nm^-1。

相对渗透率表达式为：

kl＝s³、kg＝(1-s)³

动力粘度系数表达式为：

μl＝2.414×10^-5×10^{247.8/(t-140)}

水蒸气和液态水之间的相变源项sv-l(kgm^-3s^-1)表达式为：

其中kv-l(s^-1)表示水蒸气液化速率，kl-v(s^-1)表示液态水蒸发速率，在本发明中，均取100s^-1，csat(molm^-3)表示饱和态水蒸气浓度，由饱和蒸气压计算得到：

计算离子电势和电子电势时，电化学反应参数如下：阴阳极参考电化学反应速率阴阳极反应气体参考浓度转移系数αa＝αc＝0.5，输出电压vout＝0.6v。

有效电导率计算表达式如下所示，其中微孔层和催化层经bruggemann修正，在气体扩散层内考虑纤维束平面和垂直纤维束平面电子电导率的各向异性。

气体有效扩散系数计算表达式如下所示(渗流阈值εp＝0.11)：

(3)流道内部：

考虑如下工况，流道入口阴阳极进气均完全加湿，即rh＝100％，阴阳极出口压力均为1atm，阳极进气化学计量比为ξ^a＝5.0，阴极化学计量比ζ^c＝2.0，参考电流密度i^ref＝15000am^-2，温度t＝353.15k。

(4)流道与气体扩散层交界面

计算过程中，质子交换膜燃料电池膜电极和流道的计算独立进行，将流道中计算得到的气压、气体摩尔浓度和根据气压以及液相体积分数获得的液压赋值到气体扩散层一侧，并作为膜电极计算过程中的边界条件，膜电极中计算完成后将气体扩散层中得到的通量以源项的形式赋值到流道一侧作为流道中计算过程中的源项，通过数据交换，可以保证质子交换膜燃料电池流道和膜电极质量守恒。

(5)整个计算域：

求解整体计算域能量方程时，定义极板、气体扩散层、微孔层、催化层和质子交换膜比热容分别为：1580、568、3300、3300、833jkg^-1k^-1，极板、微孔层、催化层和质子交换膜有效导热系数分别为20、1.0、1.0和0.95wm^-1k^-1，在气体扩散层内，纤维束平面内导热系数为21wm^-1k^-1，垂直纤维束平面内为1.7wm^-1k^-1。

同时，阳极和阴极熵值变化分别为δsa＝130.68jmol^-1k^-1，δsc＝32.55jmol^-1k^-1，膜态水与液态水之间相变潜热及水蒸气与液态水之间相变潜热均为h＝40650jmol^-1。

根据上述方法，通过构建三维数值模型可计算得到一定工况下质子交换膜燃料电池内部水分布情况，部分结果如附图3、4、5所示。