一种探测里德堡原子光电离显微成像的方法与流程

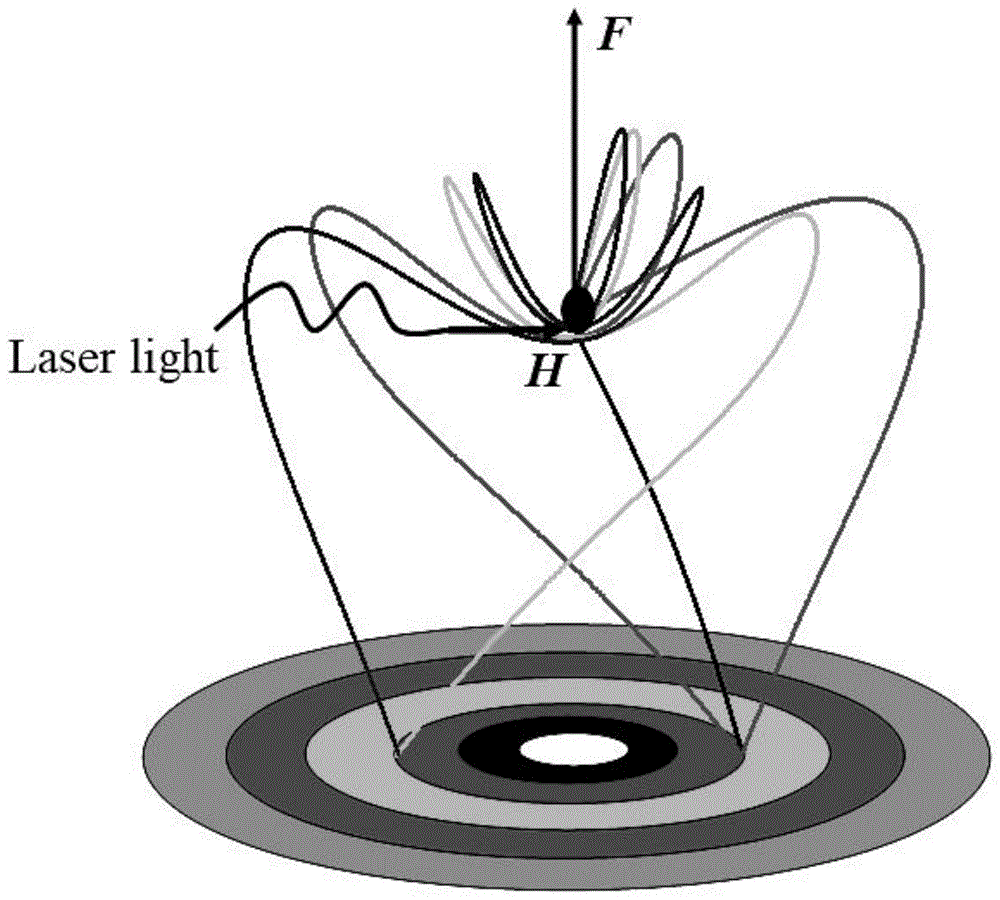
本发明属于光电信息技术领域，具体涉及一种探测里德堡原子光电离显微成像的方法。

背景技术：

随着激光技术的发展，激光与原子分子相互作用成为人类探索物理结构属性和物理规律的重要手段。随着互联网大数据和高容量信息的发展，电子学的发展出现出一定的局限性。由于光子的速度要快得多，光的频率比无线电的频率高得多，为提高传播速度和载流密度，由电子到光子的发展是必然趋势，它会使新一代信息技术的发展产生突破。目前，信息的检测、传输、存储、显示、运算和处理已由光子和电子共同参与完成，所产生的光电子学技术已被应用到信息技术领域。光电子学在国家安全与经济竞争方面有着深远意义和潜力。其中，里德堡原子在强场中的光电离过程是产生光电子的一个重要的途径。在物理学中，强场中原子光电离的研究属于原子分子物理学的前沿领域，是研究经典力学和量子力学之间联系的典型实例。进人21世纪以来，量子力学已经成为人们对原子、离子和分子等微观体系进行研究和分析的主要工具。外场中的原子发生光电离后，光电离电子将表现出丰富的动力学效应，对其研究可以促进光电子技术的发展，在实验和理论上得到了广泛地关注。随着强场物理的发展，物理学家对微观粒子波函数的观测已经从假想变成了现实。当里德堡原子在电场中发生电离时，如果在垂直于电场方向放置一探测器，就可以通过记录光电离电子的空间干涉图样和时域电子流分布，从而对光电离电子的动力学行为开展详细的研究。在空间域记录电离电子干涉图样的过程中，如果使用静电透镜将电离电子投影到位置敏感探测器上，此即所谓的光电离显微成像技术。利用光电离显微成像技术，人们可以在宏观尺度上直接观察到电子波函数的振荡结构，因此该技术提供了用宏观观测仪器直接观察微观粒子量子特性的方法。在前人的研究中，主要集中在静止的电场和磁场中里德堡原子光电离显微的研究，对于在振荡电场中里德堡原子光电离显微干涉图样的研究，国内外的研究未见报导。因此，本发明公布的里德堡原子在含时振荡电场中光电离显微成像的研究填补了国内外的研究空白。

技术实现要素：

本发明的目的在于提供一种探测里德堡原子光电离显微成像的方法，以解决上述背景技术中提出的问题。

为实现上述目的，本发明提供如下技术方案：一种探测里德堡原子光电离显微成像的方法，该方法利用含时的半经典理论方法，结合振荡电场调控电子的经典运动轨迹，通过半经典方法构造体系的波函数，进而对探测平面上光电离显微成像的干涉图样进行观测，具体包括如下步骤：

s1、用一束激光照射处在振荡电场中的原子，当氢原子中的电子吸收能量后，将电子从基态跃迁到高激发态，实现光电离过程；

s2、施加外部的振荡电场，写出光电离电子在振荡电场和库仑场中的哈密顿量h，将哈密顿量进行标度变换，得到标度变换以后的哈密顿量，为了求解哈密顿正则方程，需要消除方程在原点的奇异性，引入抛物线坐标(u，v)及其共轭动量，同时定义一个新的时间变量的定标时间变量，从而得到实际的哈密顿量h；由于库仑力和外加的振荡电场力的作用，电子运动一段时间后，可以到达与电场垂直方向的探测平面上，当有两条或者是两条以上的电子轨迹同时到达探测器平面上的同一点时，相应的电子波之间的干涉会导致探测平面上出现一系列干涉图案；

s3、假设电离电子以出射角θi从原点发射，通过数值求解含时的哈密顿正则方程，编写相应的计算程序，数值模拟光电离电子在振荡电场和库仑场中的电子轨迹，并且寻找到所有从原点出发，到达探测平面上一点的电子轨迹；

s4、利用含时的半经典理论构造电子在振荡电场中的波函数，写出第j条轨迹对应的电子波函数ψj(ρ,z0)，探测器平面上的任一给定点的波函数是到达该点的所有电子波函数的求和为了修正由于半经典近似的失败而产生的相位，引入maslov指数λj；借助于含时的半经典理论，构造里德堡原子在振荡电场中的波函数及到达探测平面上一点的电子几率密度；

s5、根据s4给出的电子的波函数，进一步推导出探测平面上一点的电子出现的几率密度，给出电子几率密度ψj(ρ,z0)的计算公式；

s6、将探测平面固定在距离原点为4.8um处，寻找到在给定的电子的标度能量和振荡频率下，到达探测平面上的一点的所有的电子轨迹，画出满足条件的ρ-θ曲线，通过编程计算出电子几率密度分布，给出光电离显微成像的三维干涉图样；

s7、改变振荡电场的频率，观察光电离显微干涉图样的变化，给出电子几率密度的分布规律；

s8、改变里德堡原子的标度能量，观察光电离显微干涉图样的变化，探寻电子几率密度的分布规律，寻找到清晰的干涉图样所满足的条件；

s9、固定里德堡原子的标度能量和振动电场的频率，改变探测平面的位置，使得探测平面距离原点的距离为2.4mm,在宏观尺度上得到清晰的光电离显微成像图样。

优选的，所述s1中，里德堡原子选取较为简单的氢原子，外加的电场为正弦振荡电场。

优选的，所述s2中，光电离电子同时受到库仑力和振荡电场力的作用，振荡电场的强度要求很强，从而将电子返回到探测平面上。

优选的，所述s4中，为了模拟电子在库仑场和振荡电场中的运动轨迹，必须编写相应的计算程序，寻找到从原子出发，到达探测平面上一点的所有光电离电子的运动轨迹。

优选的，所述s5中，里德堡原子的标度能量的变化范围为：-1.0＜ε＜-0.01；振荡电场的强度为：f＝10v/cm,振荡电场的频率变化范围为：0.01π＜ω＜0.09π。

优选的，所述s6中，探测平面距离原子的距离变化范围为：4.8μm＜z0＜2.4mm。

与现有技术相比，本发明的有益效果是：本发明所采用的半经典方法物理图像比较清晰，正弦振荡电场可以比较容易的在实验中产生，整个计算所需要的时间较短，产生的干涉图样比较清晰，可以为光电离显微的实验研究提供理论参考。

附图说明

图1为本发明中构建的里德堡氢原子在振荡电场中光电离的物理图像；

图2为本发明实施例1中得到的到达探测平面上一点(ρ＝1.0，z＝-4.0)的一些电子轨迹。

图3为本发明实施例1中得到的里德堡氢原子在给定的标度能量和振荡电场频率下光电离显微成像的三维干涉图样；

图4为本发明实施例2中里德堡氢原子在不同振荡频率的电场中得到的光电离电子的ρ-θ曲线；

图5为本发明实施例2中里德堡氢原子在不同振荡频率的电场中得到的光电离电子的二维几率密度分布曲线；

图6为本发明实施例2中里德堡氢原子在不同振荡频率的电场中得到的光电离电子的三维几率密度分布曲线；

图7为本发明实施例2中里德堡氢原子在不同振荡频率的电场中得到的光电离显微成像的三维干涉图样；

图8为本发明实施例3中里德堡氢原子在不同的标度能量下得到的光电离电子的ρ-θ曲线；

图9为本发明实施例3中里德堡氢原子在不同的标度能量下得到的光电离电子的二维几率密度分布曲线；

图10为本发明实施例3中里德堡氢原子在不同的标度能量下得到的光电离电子的三维几率密度分布曲线；

图11为本发明实施例3中里德堡氢原子在不同的标度能量下得到的光电离显微成像的三维干涉图样；

图12为本发明实施例4中在宏观尺度上观测到的里德堡氢原子在振荡电场中的光电离显微成像的三维干涉图样。

图1中：探测平面垂直于电场；在探测器平面上的同一点，几条电子轨迹可以到达，出现一组同心干涉条纹，此即光电离显微成像。

图2中：标度能量ε＝-0.1，电场频率ω＝0.1π；探测器位于z0＝-4.0s.u.≈-4.8um的平面上，图中给出了每条轨道的出射角。

图3中：图3(a)为里德堡氢原子在振荡电场中的ρ-θ曲线；图3(b)为光电离电子在探测平面上的二维电子几率密度分布曲线；图3(c)为光电离电子在探测平面上的三维几率密度分布；图3(d)为图3(c)相对应的光电离显微图像。里德堡氢原子的标度能量ε＝-0.1，电场频率ω＝0.1π，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。

图4中：里德堡氢原子的标度能量ε＝-0.1，探测器位于z0＝-4.0s.u.≈-4.8um的平面上；振荡电场的频率如下：(a)ω＝0.01π；(b)ω＝0.02π；(c)ω＝0.03π；(d)ω＝0.05π；(e)ω＝0.07π；(f)ω＝0.09π。

图5中：里德堡氢原子的标度能量ε＝-0.1，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。振荡电场的频率如下：(a)ω＝0.01π；(b)ω＝0.02π；(c)ω＝0.03π；(d)ω＝0.05π；(e)ω＝0.07π；(f)ω＝0.09π。

图6中：里德堡氢原子的标度能量ε＝-0.1，探测器位于z0＝-4.0s.u.≈-4.8um的平面上；振荡电场的频率如下：(a)ω＝0.01π；(b)ω＝0.02π；(c)ω＝0.03π；(d)ω＝0.05π；(e)ω＝0.07π；(f)ω＝0.09π。

图7中：里德堡氢原子的标度能量ε＝-0.1，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。振荡电场的频率如下：(a)ω＝0.01π；(b)ω＝0.02π；(c)ω＝0.03π；(d)ω＝0.05π；(e)ω＝0.07π；(f)ω＝0.09π。

图8中：振荡电场的频率ω＝0.05π，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。里德堡氢原子的标度能量如下：(a)ε＝-0.01；(b)ε＝-0.2；(c)ε＝-0.4；(d)ε＝-0.6；(e)ε＝-0.8；(f)ε＝-1.0。

图9中：振荡电场的频率ω＝0.05π，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。里德堡氢原子的标度能量如下：(a)ε＝-0.01；(b)ε＝-0.2；(c)ε＝-0.4；(d)ε＝-0.6；(e)ε＝-0.8；(f)ε＝-1.0。

图10中：振荡电场的频率ω＝0.05π，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。里德堡氢原子的标度能量如下：(a)ε＝-0.01；(b)ε＝-0.2；(c)ε＝-0.4；(d)ε＝-0.6；(e)ε＝-0.8；(f)ε＝-1.0。

图11中：振荡电场的频率ω＝0.05π，探测器位于z0＝-4.0s.u.≈-4.8um的平面上。里德堡氢原子的标度能量如下：(a)ε＝-0.01；(b)ε＝-0.2；(c)ε＝-0.4；(d)ε＝-0.6；(e)ε＝-0.8；(f)ε＝-1.0。

图11中：(a)里德堡氢原子在振荡电场中到达距离原子比较远的探测平面上的三维几率密度分布曲线。(b)里德堡氢原子在振荡电场中到达距离原子比较远的探测平面上的光电离显微成像图。里德堡氢原子的标度能量ε＝-0.01，振荡电场的频率ω＝0.05π，探测器位于z0＝-2000.0s.u.≈-2.4mm的平面上。

具体实施方式

下面结合实施例对本发明做进一步的描述。

以下实施例用于说明本发明，但不能用来限制本发明的保护范围。实施例中的条件可以根据具体条件做进一步的调整，在本发明的构思前提下对本发明的方法简单改进都属于本发明要求保护的范围。

本发明提供一种探测里德堡原子光电离显微成像的方法，首先将用一束激光照射氢原子，使得外层电子从基态跃迁到高激发态；然后施加外部的振荡电场，对光电离电子的运动轨迹进行调控，找到到达探测平面上一点的所有的电子轨迹；利用半经典方法构造体系的波函数，给出电子几率密度的计算公式，最终对光电离电子的几率密度进行计算。通过改变里德堡原子的标度能量、振荡电场的频率及探测平面的位置，获得清晰的光电离显微成像的干涉图样，实现在宏观尺度上直接观察到电子波函数的振荡结构。

实施例1

s1、用一束激光照射氢原子，将电子从基态跃迁到高激发态；

s2、施加外部的振荡电场，写出光电离电子在振荡电场和库仑场中的哈密顿量：

将哈密顿量进行如下的标度变换：

得到标度变换以后的哈密顿量：

为了消除上述方程在原点的奇异性，引入了抛物线坐标(u，v)及其共轭动量，定义为：

其中：

给出一种新的定标时间变量：

dτ/dt＝1/(u²+v²)(6)

我们得到实际的哈密顿量为：

h＝(u²+v²)(h-ε)(7)

假设电离电子以出射角θi从原点发射:,

θi＝tan^-1(ρ/z)＝2tan^-1(v/u)(9)

它是电子初速度与z轴正向之间的夹角,设h＝0并积分哈密顿运动方程，我们可以得到电离电子在振荡电场和库仑场中的电子轨迹。

s3、利用含时的半经典理论构造电子在振荡电场中的波函数。对于探测器平面上的任一给定点m(ρ,z0)，有多条电子轨迹可以到达。对于第j条轨迹，电子波函数表示为：

其中，aj是波函数的振幅：

经典物理量sj的定义是

γ＝f0^-1/4是标度因子，λj是maslov指数，等于(方向上的极值点的个数加上z轴的交点的个数。引入maslov指数的目的是为了修正由于半经典近似的失败而产生的相位。到达探测器上一点m(ρ,z0)处，电子的波函数ψf(ρ,z0)是通过从离子源出发到达探测平面上的所有电子轨迹相加得到的：

探测平面上给定点m(ρ,z0)处的电子几率密度分布为：

通过上式可以看出，电子在探测平面上一点的几率密度分布有两部分：第一部分是经典的电子密度分布，第二部分为到达探测器的不同经典轨迹的干涉引起的几率密度分布。

s4、固定探测平面的位置，距离原点为z0＝4.0s.u.≈4.8um,里德堡氢原子的标度能量ε＝-0.1,振荡电场的频率ω＝0.1π。通过编程，寻找到到达探测平面上一点的运动轨迹。图2给出了探测平面上的点(ρ＝1.0，z＝-4.0)的6条电子轨迹。

s5、通过编程，画出了距离原点为z0＝4.0s.u.≈4.8um的探测平面上的光电离电子的ρ-θ分布曲线；根据几率密度的计算公式，计算给出了探测平面上的电子几率密度分布。利用origin软件画图，得到了探测平面上里德堡氢原子的光电离显微成像的干涉图样，如图3所示。从图3(a)中可以看出，在探测平面上的某一点，有多条电子轨迹可以到达。整个ρ-θ曲线可以分割成不同的区域，用数字1，2，3…表示。在第一个区域，振荡电场的影响很小，电子的轨迹类似于电子在库仑场中的轨迹，呈抛物线状。电子轨迹可以直接运动到探测器表面，而不需要在ρ-z平面上旋转，属于直接轨迹。而在第二个区域，振荡电场的影响开始显现。在到达探测器平面之前，电子将环绕原子核运动一次。这些电子轨迹是间接的。在第三个区域，电子在运动到探测器平面前将会环绕原子核运动两次。其他区域的电子轨迹也可以用类似的方法来分析。图3(b)给出了探测平面上的电子几率密度分布。可以看出，由于在库仑场和振荡电场中不同电子轨迹之间的相互干涉，电子几率密度中出现了振荡结构。为了清楚地显示电子在探测器平面上的几率密度分布，我们计算了探测器平面上的三维几率密度分布，如图3(c)所示。图3(d)是对应于图3(c)的光电离显微成像，可在实际光电离显微实验中测量。在电子几率密度分布中，出现了一系列亮、暗相间的同心干涉环。亮环是由不同电子轨迹的相长干涉引起的，而暗环则是由不同电子轨迹之间的相消干涉引起的。

实施例2

与实施例1类似，区别在于步骤5中，固定探测平面的位置及里德堡氢原子的标度能量，z0＝4.0s.u.≈4.8um,里德堡氢原子的标度能量ε＝-0.1,改变振荡电场的频率，实现对光电离显微干涉成像的调控。假设振荡电场的频率在0.01π到0.09π之间变化。所得结果如图4-7所示。图4给出了在不同的振荡频率的电场中，到达探测平面上的t-ρ分布曲线。

从图4可以看出，随着振荡电场频率的增加，到达探测平面上一点的光电离电子的运动轨迹减小，并且电子到达探测平面上的最大碰撞半径减小。

图5给出了在不同的振荡频率的电场中，探测平面上的二维电子几率密度分布曲线。从图中可以看出，当振荡电场的频率很小时，振荡电场对电子运动的影响很小，到达探测器平面上的最大碰撞半径较大，电子几率密度分布范围较大。随着振荡电场频率的增加，振荡电场的影响增强，振荡电场将会限制电子在ρ-z平面上的运动，到达探测器电子轨迹会减少，并且电子到达探测平面上的最大碰撞半径减小，从而导致电子几率密度中的振荡区域减小。

图6给出了在不同的振荡频率的电场中，探测平面上的三维电子几率密度分布曲线。图7是与图6项对应的光电离显微的成像图。从图中可以看出，光电离显微成像中出现了一系列同心的环状结构，并且随着振荡电场的频率的增加，光电离显微成像的分布半径逐渐减小。

实施例3

与实施例1,2类似，区别在于步骤5中，固定探测平面的位置及振荡电场的频率，z0＝4.0s.u.≈4.8um,ω＝0.05π,改变里德堡氢原子的标度能量，实现对光电离显微干涉成像的调控。假设里德堡氢原子的标度能量在-0.01到-1.0之间变化。所得结果如图8-11所示。图8给出了当里德堡氢原子取不同的标度能量时，到达探测平面上的光电离电子的ρ-θ分布曲线。图9给出了里德堡氢原子在振荡电场中到达探测平面的二维几率密度分布曲线随标度能量的变化。图10和11给出了里德堡氢原子在振荡电场中到达探测平面的三维几率密度分布曲线及光电离显微成像随标度能量的变化。从图中可以看出，当里德堡氢原子的标度能量ε＝-0.01,改变振荡电场的频率ω＝0.05π时，光电离显微成像比较清晰。

实施例4

与实施例1,2,3类似，区别在于步骤5中，固定里德堡氢原子的标度能量ε＝-0.01，振荡电场频率ω＝0.05π，改变探测平面的位置，观察光电离显微图像的变化。将探测平面的位置放置在距离氢原子很远的距离，z0＝2000.0s.u.≈2.4mm。这一距离已经达到了宏观尺度，可以很容易在实验室中实现。如图12所示，我们仍然可以得到比较清晰的光电离显微的干涉图样。

总之，利用含时的半经典理论，本发明提供了一种探测里德堡原子光电离显微成像的方法，并通过编程计算得到了在振荡电场中里德堡氢原子在探测平面上的电子几率密度分布。结果表明：由于到达探测平面上一点的不同电子轨迹之间的相互干涉，电子几率密度分布中出现了一系列的振荡结构，并且几率密度的振荡结构取决于振荡电场的频率、标度能量和探测平面的位置。即使探测平面位于与光电离源距离很远的宏观距离，光电离显微的干涉图样也可以清楚的观察到。因此，我们的工作提供了在振荡电场中里德堡原子光电离显微成像的研究方法。在本专利中，我们选取的是里德堡氢原子，因为这个原子是最简单的，原子核外只有一个电子，分析相对简单。然而，本专利所采用的方法是通用的，可以扩展到多电子原子，如氦原子，锂原子等。因此，我们的研究提供了一种在实验上产生光电离显微成像的方法，具有很强的创新性。

尽管已经示出和描述了本发明的实施例，对于本领域的普通技术人员而言，可以理解在不脱离本发明的原理和精神的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由所附权利要求及其等同物限定。