一种基于阻尼贡献的互联电网动态稳定安控策略优化方法与流程

本发明涉及一种互联电网动态稳定的安控策略优化方法，具体涉及一种基于阻尼贡献的互联电网动态稳定安控策略优化方法。

背景技术：

由于能源资源的分布不均和用电需求的不断增长，我国互联电网的规模逐渐增大。远距离大容量输电在实现电力资源大范围支配的同时，也容易导致区域电网间的弱阻尼或负阻尼低频振荡。现代普遍采用的高放大倍数快速励磁系统能够有效提高系统静态和暂态稳定水平，但是在重负荷下可能弱化系统阻尼，引发低频振荡问题。

与单一扰动源的低频振荡不同，互联系统的振荡由于负阻尼机组数量较多，不能全部切除进行控制，而应该采用降低关键机组出力的方法。工程上对于可能激发电网低频振荡的故障，都离线制定了相应的安控策略，但是在切机对象的选择上主要依靠仿真曲线和运行人员的主观经验，缺乏严格的计算分析，难以适应电网的变化发展。

技术实现要素：

为解决上述现有技术中的不足，本发明的目的是提供一种基于阻尼贡献的互联电网动态稳定安控策略优化方法，该方法将发电机在某一振荡模式中的阻尼贡献量化，对机组进行切机优先度排序，优化安控策略的实施效果，减小控制代价，能够应用于离线方案的制定和在线振荡监测。

本发明的目的是采用下述技术方案实现的：

本发明提供一种基于阻尼贡献的互联电网动态稳定安控策略优化方法，其特征在于，所述方法包括下述步骤：

1)提取机组参数和电气量数据，确定阻尼贡献指标；

2)计算未知电气量；

3)辨识电气量稳态运行点；

4)辨识电磁阻尼转矩系数和机械阻尼转矩系数；

5)计算阻尼贡献指标；

6)生成电网动态稳定安控策略。

进一步地，所述步骤1)中，机组参数包括定子电阻、直轴暂态电抗和交轴同步电抗，电气量数据包括机端电压、机端电流、发电机机械功率、发电机转子角度和发电机转子频率；确定阻尼贡献指标包括：

发电机直轴暂态电动势变化量ΔE′_q和机械力矩变化量ΔT_m分解成同步力矩和阻尼力矩叠加的形式，即：

ΔE′_q＝K_eΔδ+D_eΔω (1)

ΔT_m＝K_mΔδ+D_mΔω (2)

其中：Δδ为发电机功角相对于稳态运行点δ₀的变化量；Δω为发电机转子速度相对于稳态运行点ω₀的变化量；K_e为发电机直轴暂态电动势变化量的电磁同步力矩系数；D_e为发电机直轴暂态电动势变化量的电磁阻尼转矩系数；K_m为机械力矩变化量的电磁同步力矩系数；D_m为机械力矩变化量的电磁阻尼转矩系数；K_eΔδ为发电机直轴暂态电动势变化量的电磁同步力矩分量；D_eΔω为发电机直轴暂态电动势变化量的电磁阻尼力矩分量；K_mΔδ为机械力矩变化量的电磁同步力矩分量；

式(1)和式(2)中的同步力矩分量与低频振荡无关，将其中的同步力矩分量和阻尼力矩分量解耦，对ΔE′_q和ΔT_m中阻尼力矩分量的作用进行累积计算；式(1)中的参数D_e反映励磁绕组、励磁系统和PSS的综合阻尼，式(2)中的参数D_m反映调速系统的阻尼，则(D_e-D_m)Δω与Δω的相位关系反映机组控制系统整体的阻尼性质；

定义从t₁时刻到t₂时刻发电机阻尼状态的量化表达式为：

若式(3)的计算结果为负，则说明发电机组在t₁到t₂的时间段内处于负阻尼状态，绝对值越大说明负阻尼越严重；

将式(3)表示的阻尼状态与发电机出力相乘，作为真正的阻尼贡献，t₁时刻到t₂时刻的发电机阻尼贡献指标如式(4)所示：

式(4)的负数绝对值越大，表明发电机组在振荡中越关键，优先切除；P_e为发电机出力。

进一步地，所述步骤2)中，未知电气量包括发电机直轴暂态电动势和机械转矩；发电 机直轴暂态电动势利用各采样时刻的机端电压机端电流定子电阻R_a、直轴暂态电抗X′_d和交轴同步电抗X_q进行计算，计算公式如下：

式中：E_Q为发电机虚构电动势；δ为发电机功角；δ′为暂态电动势对于母线电压的相对角；为暂态电动势；E′_q为直轴暂态电动势幅值；E′暂态电动势幅值；

发电机机械转矩按照式(6)进行计算：

式中：T_m为发电机机械转矩，P_m为发电机机械功率，ω为发电机转子频率。

进一步地，所述步骤3)中，将振荡曲线的中轴线作为发电机的稳态运行点，通过拟合振荡曲线的上下包络线来求取振荡中轴线；辨识电气量稳态运行点包括下述步骤：

①辨识振荡曲线转折点：

将采样点i的切线斜率f′(t_i)和切线斜率变化速度f″(t_i)分别以一次差分和二次差分的形式近似表示：

上包络线转折点的切线斜率变化速度为极小值点，下包络线转折点的切线斜率变化速度为极大值点，如式(8)所示，根据如下判据找出振荡曲线的转折点：

式中，t_i为电气量第i个采样点对应的时间；f(t_i)为第i个采样点的电气量数值；

②包络线拟合：

假设振荡曲线的上包络线共有m个转折点，表示为[x_j,f(x_j)](j＝1,2…m)；构造上包络线的三次样条插值函数S_up(t)求取振荡曲线的上包络线，其表达式为：

S_up(t)＝a_jt³+b_jt²+c_jt+d_j

(9)

t∈[x_j,x_j+1] j＝1,2…m-1

式中：a_j、b_j、c_j、d_j均为三次样条插值函数S_up(t)的系数；x_j,x_j+1分别为m个转折点中的第j个转折点和j+1个转折点；

根据插值条件、连续性条件和边界条件求取待定系数；插值条件为：

S_up(x_j)＝f(x_j) j＝1,2,3…m (10)

连续性条件为：

S_up(x_j+0)＝S_up(x_j-0) j＝2,3…m-1

S′_up(x_j+0)＝S′_up(x_j-0) j＝2,3…m-1 (11)

S″_up(x_j+0)＝S″_up(x_j-0) j＝2,3…m-1

边界条件为：

S′_up(x₁)＝f′(x₁) S′_up(x_m)＝f′(x_m) (12)

式中：f′(x₁)和f′(x_m)均为振荡曲线两端的一阶导数值；

假设振荡曲线的下包络线共有m个转折点，表示为[x_k,f(x_k)](k＝1,2…m)；构造下包络线的三次样条插值函数S_down(t)求取振荡曲线的上包络线，其表达式为：

S_down(t)＝a_kt³+b_kt²+c_kt+d_k

(13)

t∈[x_k,x_k+1] k＝1,2…m-1

根据插值条件、连续性条件和边界条件求取待定系数；插值条件为：

S_down(x_k)＝f(x_k) k＝1,2,3…m (14)

连续性条件为：

S_down(x_k+0)＝S_down(x_k-0) k＝2,3…m-1

S′_down(x_k+0)＝S′_down(x_k-0) k＝2,3…m-1 (15)

S″_down(x_k+0)＝S″_down(x_k-0) k＝2,3…m-1

边界条件为：

S′_down(x₁)＝f′(x₁) S′_down(x_m)＝f′(x_m) (16)

式中：a_k、b_k、c_k、d_k均为三次样条插值函数S_down(t)的系数；x_k,x_k+1分别为m个转折点中的第k个转折点和k+1个转折点；

③稳态点求取：

以同一时间下，上下包络线三次样条差值函数的中值作为时间点的稳态运行点，t_i时刻的有功功率稳态运行点：

式中：P_s,i为t_i时刻的有功功率稳态运行点。

进一步地，所述步骤4)中，采用最小二乘法的矩阵形式辨识电磁阻尼转矩系数D_e和机械阻尼转矩系数D_m，在10°以内的振荡幅度下，发电机的同步转矩系数和阻尼转矩系数均为常数；将振荡数据等距分段，采用分段辨识、逐段累加的方法计算发电机阻尼贡献；辨识电磁阻尼转矩系数D_e时，取数据的采样间隔为20ms，以相邻的10组[ΔE′_q,Δδ,Δω]数据为一个单位进行参数辨识，最小二乘法的矩阵形式如下：

B＝(X^TX)^-1X^TY (18)

式(18)中，各矩阵内容如下所示：

式中：ΔE′_qh为发电机直轴暂态电动势变化量，Δδ_h为发电机功角相对于稳态运行点δ₀的变化量；Δω_h为发电机转子速度相对于稳态运行点ω₀的变化量；h＝1,2,…10；B为发电机电磁转矩和阻尼转矩系数矩阵；X为功角变化量和频率变化量矩阵；X^T为X的转置矩阵；Y为直轴暂态电抗矩阵；计算机械力矩变化量的电磁同步力矩系数K_m和机械力矩变化量的电磁阻尼转矩系数D_m时，时，将Y和B替换为：

式中：ΔT_mh为机械力矩变化量。

进一步地，所述步骤5)中，计算阻尼贡献指标包括：利用参数辨识方法，将电磁力矩和机械力矩中的阻尼力矩成分单独提取出来，将控制系统的综合阻尼力矩与转速变化量的相位关系的积分作为一段时间内发电机阻尼状态的量化值，将阻尼状态与额定有功出力的乘积作为该时间段内发电机阻尼贡献的量化值。

进一步地，所述步骤6)中，生成电网动态稳定安控策略包括：基于阻尼贡献指标对发 电机的切机优先度进行排序，生成优先度列表，按照排序生成电网动态稳定安控策略，优化电网动态稳定安控策略实施效果，减少控制代价。

本发明提供的技术方案具有的优异效果是：

(1)本发明提供的方法综合考虑了发电机励磁系统和调速系统的影响，将发电机在振荡中的阻尼贡献量化，明确给出应优先考虑切除的机组，极大地提升了安控方案的实施效果，且不受故障形式和电网结构变化的影响，适应性较强。

(2)基于发电机的阻尼特性分析，利用最小二乘法将电磁转矩和机械转矩中的同步转矩和阻尼转矩解耦。阻尼贡献指标略去了电磁转矩与阻尼转矩中与抑制低频振荡无关的分量，与目前已提出的反应机组阻尼状态的指标相比，具有更高的精确度。

附图说明

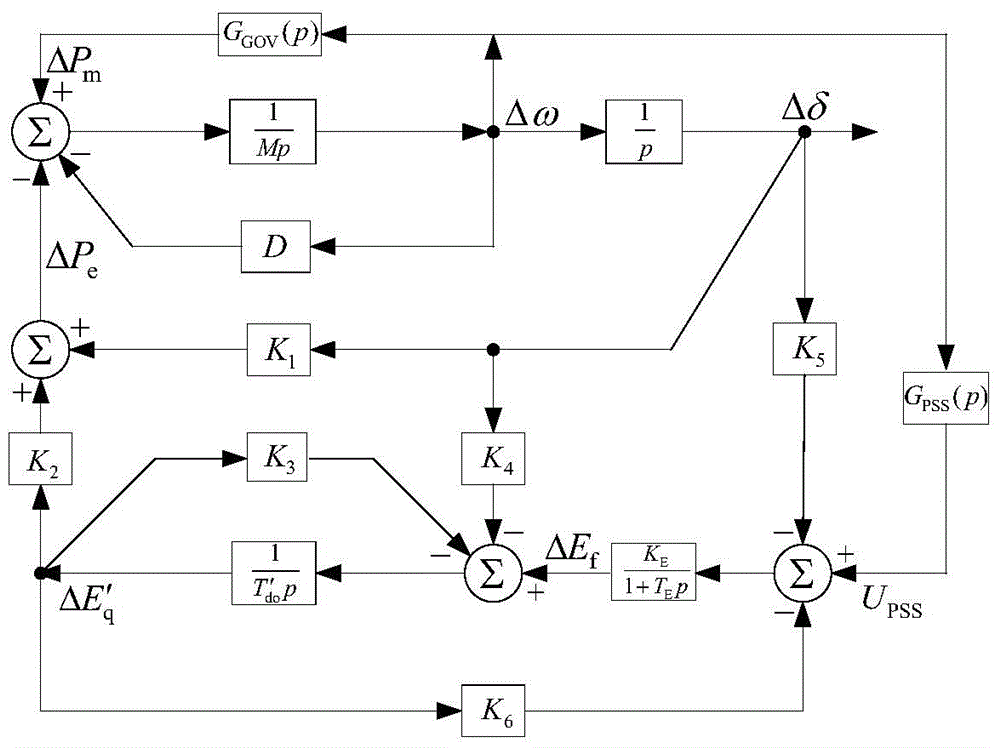
图1是本发明提供的单机无穷大系统传递函数框图；

图2是本发明提供的基于阻尼贡献的互联电网动态稳定安控策略优化方法的流程图；

图3是本发明提供的原方案以及利用本发明方案实施后外呼丰断面外送功率曲线图。

具体实施方式

下面结合附图对本发明的具体实施方式作进一步的详细说明。

以下描述和附图充分地示出本发明的具体实施方案，以使本领域的技术人员能够实践它们。其他实施方案可以包括结构的、逻辑的、电气的、过程的以及其他的改变。实施例仅代表可能的变化。除非明确要求，否则单独的组件和功能是可选的，并且操作的顺序可以变化。一些实施方案的部分和特征可以被包括在或替换其他实施方案的部分和特征。本发明的实施方案的范围包括权利要求书的整个范围，以及权利要求书的所有可获得的等同物。在本文中，本发明的这些实施方案可以被单独地或总地用术语“发明”来表示，这仅仅是为了方便，并且如果事实上公开了超过一个的发明，不是要自动地限制该应用的范围为任何单个发明或发明构思。

互联电网低频振荡机理如下：

在低频振荡中，系统的总能量与振幅对应，消耗能量的元件对振荡衰减的贡献为正，具有正阻尼，而产生能量的元件是振荡源，具有负阻尼。在互联系统发生低频振荡时，可能有相当数量的机组对振荡衰减的贡献为负。在电网发生扰动后，发电机的PSS、励磁绕组、阻 尼绕组以及机械系统均能提供一定的正阻尼，而励磁系统和调速器则有可能在一定情况下表现为负阻尼，弱化系统整体阻尼，从而引起弱阻尼或负阻尼低频振荡。

图1为单机无穷大系统线性化模型的传递函数框图，发电机计及励磁系统、调速系统和PSS动态。

发电机励磁系统通过改变电磁力矩影响转子运动。电磁力矩变化量ΔT_e可以分解成同步力矩和阻尼力矩两个分量，即：

ΔT_e＝K₁Δδ+K₂ΔE′_q

＝K_eΔδ+D_eΔω

式中：Δδ为发电机功角相对于稳态运行点δ₀的变化量；Δω为发电机转子速度相对于稳态运行点ω₀的变化量；K_e为电磁同步力矩系数；D_e为电磁阻尼力矩系数。

同步力矩主要影响振荡频率，阻尼力矩则与抑制低频振荡直接相关。D_e>0时，电磁力矩中产生一个和速度变化量Δω同相的正阻尼力矩成分，有助于抑制低频振荡。

在图1中，参数K₅实质是机端电压对功角的偏导数，该参数在发电机重负荷(功角较大)时可能为负值。K₅<0时，ΔT_e在Δω-Δδ相平面上处于第III、IV象限，即D_e＜0，励磁系统阻尼为负。

在联络线远距离大容量输电的情况下，送受端端发电机功角较大。特别是在输电断面线路跳闸后，两侧系统电气距离加大，送端发电机功角也相应加大，此时送端机组的励磁系统有可能提供负阻尼。发生互联电网低频振荡时，大量送端机组将呈现负阻尼。

调速系统通过改变机械力矩影响转子运动，它对动态稳定的影响与其本身的参数配置、振荡频率和系统参数等因素有关。与电磁力矩类似，原动机的机械力矩变化量ΔT_m也能分解为同步力矩和阻尼力矩两个分量，即：

ΔT_m＝K_mΔδ+D_mΔω (2)

式中：K_m为机械同步力矩系数；D_m为机械阻尼力矩系数。

与电磁力矩不同的是，由于机械力矩是加速力矩，当Δω＞0时，正常的调速器应该产生一个与Δω反相的力矩分量，阻止转子速度继续增加。因此，当D_m＜0时，ΔT_m在Δω-Δδ相平面上处于第III、IV象限，调速器向系统提供正阻尼。

本发明提供一种基于阻尼贡献的互联电网动态稳定安控措施优化方法，将发电机在某一振荡模式中的阻尼贡献量化，对机组进行切机优先度排序，优化安控策略的实施效果，减小 控制代价，能够应用于离线方案的制定和在线振荡监测，其流程图如图2所示，包括下述步骤：

1)提取机组参数和电气量数据，确定阻尼贡献指标；

机组参数包括定子电阻、直轴暂态电抗和交轴同步电抗，电气量数据包括机端电压、机端电流、发电机机械功率、发电机转子角度和发电机转子频率；确定阻尼贡献指标包括：

图1中，K₂一般是大于0的实数，因此ΔE′_q即可反应发电机电磁转矩的阻尼性质，ΔE′_q同样可以分解成同步力矩和阻尼力矩叠加的形式，即：

ΔE′_q＝K_eΔδ+D_eΔω (1)

式(2)中的参数D_e反映了励磁绕组、励磁系统和PSS的综合阻尼，再计及调速系统的阻尼作用，则(D_e-D_m)Δω与Δω的相位关系反映了机组控制系统整体的阻尼性质；式(1)和式(2)中的同步力矩分量与低频振荡无关，将其中的同步力矩和阻尼力矩解耦，单独对ΔE′_q和ΔT_m中阻尼力矩的作用进行累积计算；其中：ΔE′_q为发电机电磁转矩，Δδ为发电机功角相对于稳态运行点δ₀的变化量；Δω为发电机转子速度相对于稳态运行点ω₀的变化量；K_e为电磁同步力矩系数；D_e为电磁阻尼转矩系数；

定义从t₁时刻到t₂时刻发电机阻尼状态的量化表达式为：

若式(3)的计算结果为负，则说明发电机组在t₁到t₂的时间段内处于负阻尼状态，绝对值越大说明负阻尼越严重；D_m为机械阻尼转矩系数，

发电机的振荡能量最终是以功率扰动的形式传播到网络中的，机组容量不同，其影响程度也不同。因此，机组的阻尼贡献除了与机组本身的阻尼特性有关外，还与发电机出力P_e有关。为考虑该因素的影响，将式(3)表示的阻尼状态与发电机出力相乘，作为真正的阻尼贡献，t₁时刻到t₂时刻的发电机阻尼贡献指标如式(4)所示：

式(4)的负数绝对值越大，表明发电机组在振荡中越关键，应优先考虑切除；P_e为发电机出力。

2)计算未知电气量；

未知电气量包括发电机直轴暂态电动势和机械转矩；发电机直轴暂态电动势无法直接获 得，利用各采样时刻的机端电压机端电流定子电阻R_a、直轴暂态电抗X′_d和交轴同步电抗X_q进行计算，计算公式如下：

E_Q为发电机虚构电动势、δ为发电机功角、δ′为暂态电动势对于母线电压的相对角、为暂态电动势、E′_q为直轴暂态电动势幅值、E′暂态电动势幅值；

发电机机械转矩也无法直接获得，但是机械功率可以直接读取，可按照式(6)进行计算：

T_m为发电机机械转矩、P_m为发电机机械功率、ω为发电机转子频率。

3)辨识电气量稳态运行点；

图1中各电气量变化量都是相对于稳态运行点而言的。在系统发生大的扰动后，各发电机将从原来的稳态运行点振荡过渡到新的稳态运行点，因此不同时刻的ΔE′_q、Δδ和Δω计算应采用不同的稳态值。近似认为振荡曲线的中轴线即为其稳态运行点，通过拟合振荡曲线的上下包络线来求取振荡中轴线。稳态点辨识分为“转折点”辨识、包络线拟合和振荡曲线中轴线求取3个步骤。

①辩识振荡曲线“转折点”；在电力系统漂移振荡中，有些振荡曲线有明显的极大值和极小值，也有一些曲线斜率始终为正。拟合振荡曲线的上下包络线时，需穿过曲线的“转折点”，这些“转折点”是在一个振荡周期内斜率变化速度最快的点。将采样点i的切线斜率f′(t_i)和切线斜率变化速度f″(t_i)分别以一次差分和二次差分的形式近似表示：

上包络线转折点的切线斜率变化速度为极小值点，下包络线转折点的切线斜率变化速度为极大值点，如式(8)所示，根据如下判据找出振荡曲线的转折点：

式中，t_i为电气量第i个采样点对应的时间；f(t_i)为第i个采样点的电气量数值；

假设振荡曲线的上包络线共有m个转折点，表示为[x_j,f(x_j)](j＝1,2…m)；构造上包络线的三次样条插值函数S_up(t)求取振荡曲线的上包络线，其表达式为：

S_up(t)＝a_jt³+b_jt²+c_jt+d_j

(9)

t∈[x_j,x_j+1] j＝1,2…m-1

式中：a_j、b_j、c_j、d_j均为三次样条插值函数S_up(t)的系数；x_j,x_j+1分别为m个转折点中的第j个转折点和j+1个转折点；

根据插值条件、连续性条件和边界条件求取待定系数；插值条件为：

S_up(x_j)＝f(x_j) j＝1,2,3…m (10)

连续性条件为：

S_up(x_j+0)＝S_up(x_j-0) j＝2,3…m-1

S′_up(x_j+0)＝S′_up(x_j-0) j＝2,3…m-1 (11)

S″_up(x_j+0)＝S″_up(x_j-0) j＝2,3…m-1

边界条件为：

S′_up(x₁)＝f′(x₁) S′_up(x_m)＝f′(x_m) (12)

式中：f′(x₁)和f′(x_m)为振荡曲线两端的一阶导数值；

假设振荡曲线的下包络线共有m个转折点，表示为[x_k,f(x_k)](k＝1,2…m)；构造下包络线的三次样条插值函数S_down(t)求取振荡曲线的上包络线，其表达式为：

S_down(t)＝a_kt³+b_kt²+c_kt+d_k

(13)

t∈[x_k,x_k+1] k＝1,2…m-1

根据插值条件、连续性条件和边界条件求取待定系数；插值条件为：

S_down(x_k)＝f(x_k) k＝1,2,3…m (14)

连续性条件为：

S_down(x_k+0)＝S_down(x_k-0) k＝2,3…m-1

S′_down(x_k+0)＝S′_down(x_k-0) k＝2,3…m-1 (15)

S″_down(x_k+0)＝S″_down(x_k-0) k＝2,3…m-1

边界条件为：

S′_down(x₁)＝f′(x₁) S′_down(x_m)＝f′(x_m) (16)

式中：a_k、b_k、c_k、d_k均为三次样条插值函数S_down(t)的系数；x_k,x_k+1分别为m个转折点中的第k个转折点和k+1个转折点。

③稳态点求取

以同一时间下，上下包络线三次样条差值函数的中值作为时间点的稳态运行点，t_i时刻的有功功率稳态运行点：

式中：P_s,i为t_i时刻的有功功率稳态运行点。

4)辨识电磁阻尼转矩系数和机械阻尼转矩系数；

采用最小二乘法的矩阵形式辨识电磁阻尼转矩系数D_e和机械转矩系数D_m，在10°以内的振荡幅度()下，发电机的同步转矩系数和阻尼转矩系数均为常数；将振荡数据等距分段，采用分段辨识、逐段累加的方法计算发电机阻尼贡献；辨识电磁阻尼转矩系数D_e时，取数据的采样间隔为20ms，以相邻的10组[ΔE′_q,Δδ,Δω]数据为一个单位进行参数辨识，最小二乘法的矩阵形式如下：

B＝(X^TX)^-1X^TY (18)

式(18)中，各矩阵内容如下所示：

式中：ΔE′_qh为发电机直轴暂态电动势变化量，Δδ_h为发电机功角相对于稳态运行点δ₀的变化量；Δω_h为发电机转子速度相对于稳态运行点ω₀的变化量；h＝1,2,…10；B为发电机电磁转矩和阻尼转矩系数矩阵；X为功角变化量和频率变化量矩阵；X^T为X的转置矩阵；Y为直轴暂态电抗矩阵；计算机械同步转矩系数K_m和机械阻尼转矩系数D_m时，将Y和B替换为：

式中：ΔT_mh为机械力矩变化量。

5)计算阻尼贡献指标；计算阻尼贡献指标包括：利用参数辨识方法，将电磁力矩和机械力矩中的阻尼力矩成分单独提取出来，将控制系统的综合阻尼力矩与转速变化量的相位关系的积分作为一段时间内发电机阻尼状态的量化值，将阻尼状态与额定有功出力的乘积作为该时间段内发电机阻尼贡献的量化值。

6)生成电网动态稳定安控策略，包括：基于阻尼贡献指标对发电机的切机优先度进行排序，生成优先度列表，按照排序生成电网动态稳定安控策略，优化电网动态稳定安控策略实施效果，减少控制代价。

实施例

结合附图2，说明电网动态稳定安控策略优化方法的具体实施过程。

(1)案例介绍

以蒙西电网为例，检修永圣域—丰泉三回线中的一回，呼丰断面(武川—察右中、旗下营—汗海和永圣域—丰泉)功率为4724MW。设置永圣域—丰泉另外两回线路N-2故障，蒙西电网将发生增幅振荡，振荡频率为0.33Hz，阻尼比为-0.0023。现有安控方案为切除河西电厂1#机组、煤矸电厂3#、4#机组和京泰电厂1#机组，总切除量为1560MW。

(2)提取低频振荡发生后，送端可控机组的有功功率P_e，机械功率P_m、定子电阻R_a、直轴暂态电抗X′_d、交轴同步电抗X_q，以及互联电网发生振荡后各个时刻的机械转矩T_m、机端电压机端电流转子角度δ和转速ω；

(3)计算各个时刻的发电机交轴暂态电动势E′_q，机械转矩T_m；

(4)相关电气量稳态点辨识；

(5)采用最小二乘法辨识各时间段的电磁阻尼转矩系数和机械阻尼转矩系数；

(6)计算各发电机的阻尼贡献，结果如下：

表1 发电机阻尼贡献指标

(7)生成安控方案

由表1可知，阻尼贡献指标较大的机组是布连1#机组、河西1#机组和河西2#机组。现有安控方案实施后达到的阻尼比为0.017，而按照阻尼贡献指标排序进行控制时，只需切除1060MW的功率即可达到同样的控制效果。其中，布连1#机组切除660MW，河西1#机组切除400MW，切机总量减少了500MW，占原方案切机总量的32％。两种方案实施后外呼丰断面外送功率曲线如图3所示。

图3中，原方案实施后外送断面平均功率约为3493MW，改进方案则为3890MW，控制代价相比原方案大幅度减少。因此，本发明提供的方法完全可以为离线方案制定提供严格的数据分析。而应用于在线振荡监测与控制时时，本发明提供的方法能更好地适应故障形式、电网参数和结构的变化，根据实时数据给出优化的切机顺序，提高系统阻尼。

以上实施例仅用以说明本发明的技术方案而非对其限制，尽管参照上述实施例对本发明进行了详细的说明，所属领域的普通技术人员依然可以对本发明的具体实施方式进行修改或者等同替换，这些未脱离本发明精神和范围的任何修改或者等同替换，均在申请待批的本发明的权利要求保护范围之内。