一种全局稳定的电机伺服系统输出反馈鲁棒控制方法与流程

本发明涉及电机位置伺服控制系统
技术领域：
，具体涉及一种全局稳定的电机伺服系统输出反馈鲁棒控制方法。
背景技术：
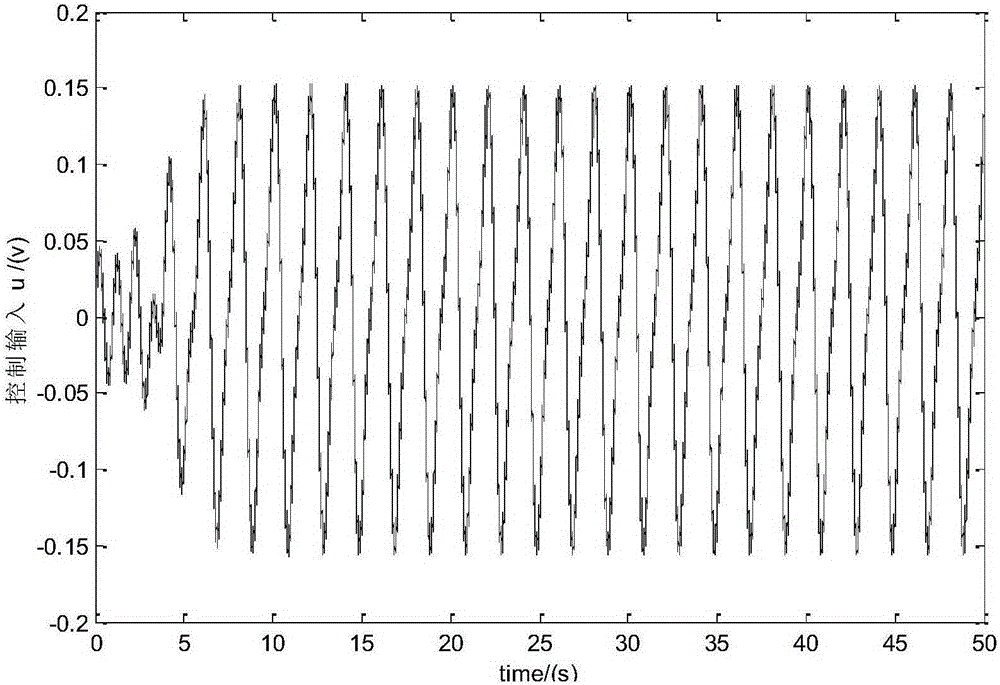
：直流电机具有响应快速、调速范围广，易于实现速度平滑调节，调速时的能量损耗较小以及过载、启动、制动转矩大，易于控制，可靠性高等优点，因而在工农业生产，交通运输，国防，航空航天，医疗卫生，商务办公设备以及家用电器中应用广泛。随着工业发展的需求，高精度的运动控制已成为现代直流电机的主要发展方向。然而，由于电机系统中存在着很多的模型不确定性，尤其是不确定非线性，这些不确定性因素增加了控制系统的设计难度。为了处理电机系统中的不确定非线性问题，提高电机伺服系统的控制性能，鲁棒控制作为一种主要处理方法，已被广泛应用于实际工程应用。然而，所有上述方法均基于全状态反馈开展控制器设计，在运动控制中，不仅需要位置信号，还需要速度和/或加速度信号。但在许多实际系统中，受机械结构、体积、重量及成本限制，往往仅位置信息可知。此外，即便速度及加速度信号可以获得，也存在严重的测量噪声，进而恶化全状态反馈控制器可以获得的性能。非线性控制应用中所存在的这些实际问题，导致了PID控制至今在电机控制领域仍处于主导地位。但是，在现代工业时代的新需求下，PID越来越难以满足日益追求的高性能控制。因此，迫切需要设计非线性输出反馈控制策略。技术实现要素：本发明针对电机位置伺服系统中存在的不确定非线性问题，在只有系统位移可知的前提下，提出一种全局稳定的电机伺服系统输出反馈鲁棒控制方法。为实现上述目的，本发明所采用的技术方案如下:一种全局稳定的电机伺服系统输出反馈鲁棒控制方法，包括以下步骤：步骤一、建立电机位置伺服系统模型:my··=kfu-by·-f(y,y·,t)---(1)]]>其中y表示角位移，m表示惯性负载，kf表示扭矩常数，u是系统控制输入，b代表粘性摩擦系数，f代表其他未建模干扰，包括非线性摩擦、外部干扰以及未建模动态；将式(1)转换成状态空间形式，如下：x·1=x2x·2=θ1u-θ2x2-d(x,t)---(2)]]>其中表示位置和速度的状态向量；参数集θ＝[θ1,θ2]T，其中θ1＝kf/m，θ2＝b/m，d＝f/m表示集中干扰；系统中的参数m，kf，b是未知的，且系统的未建模动态和干扰总是有界的，因而，以下假设总是成立的：假设1：参数θ满足：θ∈Ωθ=Δ{θ:θmin≤θ≤θmax}---(3)]]>其中θmin＝[θ1min,θ2min]T，θmax＝[θ1max,θ2max]T，它们都是已知的，此外θ1min>0，θ2min>0；假设2：d(x,t)是已知有界的，即|d(x,t)|≤δd(4)其中δd已知；让yd表示系统参考轨迹，假设其是二阶可导的，且二阶导有界，即L是已知正数。；步骤二、设计基于一致鲁棒精确微分器的全局稳定电机高精度输出反馈控制器，具体步骤如下：步骤二(一)、根据公式(2)构建电机的一致鲁棒精确微分器首先，由系统的已知输出状态x1设计一致鲁棒精确微分器，用于估计系统的未知状态x2，此微分器不依赖于系统输入和参数估计值，如下设计一致鲁棒精确微分器：x^·1=x^2-c1μ1(x~1)x^·2=-c2μ2(x~1)---(5)]]>其中x1，x2分别表示输出角位移和角速度，分别为x1，x2的估计值，c1，c2为待调整正参数，和分别为：μ1(x~1)=b1|x~1|12sign(x~1)+b2|x~1|32sign(x~1)μ2(x~1)=b122sign(x~1)+2b1b2x~1+3b222|x~1|2sign(x~1)---(6)]]>其中增益b1,b2>0,此外sign(·)=1,if·≥0-1,if·<0---(7)]]>由式(2)和(5)可得估计误差动态如下：x~·1=-c1μ1(x~1)+x~2,x~·2=-c2μ2(x~1)-y··---(8)]]>步骤二(二)、设计基于一致鲁棒精确微分器的全局稳定电机高精度输出反馈控制器定义变量如下：z2=z·1+k1z1=x2-x2eqx2eq=x·1d-k1z1---(15)]]>其中z1＝x1-x1d(t)是输出跟踪误差，k1>0是一个反馈增益；由于G(s)＝z1(s)/z2(s)＝1/(s+k1)是一个稳定的传递函数，当z2趋于0时，z1必然也趋于0，接下来的控制器设计，将以使z2趋于0为主要目标；对式(15)微分并把式(2)代入，可得：z·2=θ1u-θ2x2-x·2eq+d(x,t)---(16)]]>基于估计状态的控制器如下：u＝(ua+us)/θ1n,us＝us1+us2ua=x·^2eq+θ2nx^2---(17)]]>us1=-k2(x^2-x2eq)]]>其中其中k2>0是一个反馈增益；把式(17)代入式(16)，可得z2的动态方程：z·2=-k2(x^2-x2eq)+us2-(θ1n-θ1)u+(θ2n-θ2)x^2+d(x,t)+θ2x~2-k2x~2---(18)]]>由假设1可知，存在Us2满足如下条件：z2us2-(θ1n-θ1)u+(θ2n-θ2)x^2+ks1x~2+θ2x~2-k2x~2+d≤σ1---(19)]]>z2us2≤0其中σ1>0是一个设计参数，在此给出Us2的一个形式：令g为如下函数us2=-ks1z2=Δ-g2z2/(4σ1)---(20)]]>其中θm＝θmax-θmin，由此设计如下的Us2us2=-ks1(x^2-x2eq)=Δ-g2(x^2-x2eq)/(4σ1)---(21)]]>其中ks1为一个非线性增益；步骤三、调节电机控制律u的参数k1，k2，b1，b2，c1，c2使得系统满足控制性能指标。本发明的有益效果是：在只有电机角位移可测的前提下，针对存在不确定非线性的直流电机位置伺服控制系统，提出了一种基于一致鲁棒精确微分器的输出反馈鲁棒控制算法。本发明设计的一致鲁棒精确微分器不依赖于系统输入和参数的估计值，只以系统的输出作为微分器输入，其结构相对简单，易于实现。此外，还设计了鲁棒控制器以消除系统的不确定非线性。理论分析表明，所提出的算法能够保证整个闭环系统的稳定性和跟踪精度。仿真结果验证了所提出控制方法的有效性。应当理解，前述构思以及在下面更加详细地描述的额外构思的所有组合只要在这样的构思不相互矛盾的情况下都可以被视为本公开的发明主题的一部分。另外，所要求保护的主题的所有组合都被视为本公开的发明主题的一部分。结合附图从下面的描述中可以更加全面地理解本发明教导的前述和其他方面、实施例和特征。本发明的其他附加方面例如示例性实施方式的特征和/或有益效果将在下面的描述中显见，或通过根据本发明教导的具体实施方式的实践中得知。附图说明附图不意在按比例绘制。在附图中，在各个图中示出的每个相同或近似相同的组成部分可以用相同的标号表示。为了清晰起见，在每个图中，并非每个组成部分均被标记。现在，将通过例子并参考附图来描述本发明的各个方面的实施例，其中：图1是电机系统的示意图。图2是干扰作用下控制器输入电压u曲线的示意图，控制器输入电压满足-10V～+10V的输入范围，符合实际应用。图3a-3b分别是状态和其估计状态曲线的示意图。图4是指令信号和控制器跟踪误差曲线的示意图。具体实施方式为了更了解本发明的技术内容，特举具体实施例并配合所附图式说明如下。在本公开中参照附图来描述本发明的各方面，附图中示出了许多说明的实施例。本公开的实施例不必定意在包括本发明的所有方面。应当理解，上面介绍的多种构思和实施例，以及下面更加详细地描述的那些构思和实施方式可以以很多方式中任意一种来实施，这是应为本发明所公开的构思和实施例并不限于任何实施方式。另外，本发明公开的一些方面可以单独使用，或者与本发明公开的其他方面的任何适当组合来使用。下面结合附图1说明本实施方式，本实施方式所述一种全局稳定的电机伺服系统输出反馈鲁棒控制方法的具体步骤如下：步骤一、建立电机位置伺服系统模型，在直流电机伺服系统中，由于电流的动态响应高， 因而在模型的推导过程中，忽略系统的电流环动态。根据牛顿第二定律，系统动力学模型如下：my··=kfu-by·-f(y,y·,t)---(1)]]>其中y表示角位移，m表示惯性负载，kf表示扭矩常数，u是系统控制输入，b代表粘性摩擦系数，f代表其他未建模干扰，比如非线性摩擦、外部干扰以及未建模动态。把式(1)写成状态空间形式，如下：x·1=x2x·2=θ1u-θ2x2-d(x,t)---(2)]]>其中表示位置和速度的状态向量。参数集θ＝[θ1,θ2]T，其中θ1＝kf/m，θ2＝b/m，d＝f/m表示集中干扰。虽然系统参数m，kf，b是未知的，且不能对不确定非线性d(x,t)进行明确建模。但系统的大致信息是可以知道的，而且系统的未建模动态和干扰总是有界的。因而，以下假设总是成立的：假设1：参数θ满足：θ∈Ωθ=Δ{θ:θmin≤θ≤θmax}---(3)]]>其中θmin＝[θ1min,θ2min]T，θmax＝[θ1max,θ2max]T，它们都是已知的，此外θ1min>0，θ2min>0。假设2：d(x,t)是已知有界的，即|d(x,t)|≤δd(4)其中δd已知。让yd表示系统参考轨迹，假设其是二阶可导的，且二阶导有界，即L是已知正数。步骤二、设计基于一致鲁棒精确微分器的全局稳定电机高精度输出反馈控制器的具体步骤如下：步骤二(一)、根据公式(2)构建电机的一致鲁棒精确微分器。首先，由系统的已知输出状态x1设计一致鲁棒精确微分器，用于估计系统的未知状态x2，此微分器不依赖于系统输入和参数估计值。如下设计一致鲁棒精确微分器：x^·1=x^2-c1μ1(x~1)x^·2=-c2μ2(x~1)---(5)]]>其中x1，x2分别表示输出角位移和角速度，分别为x1，x2的估计值，c1，c2为待调整正参数。和分别为μ1(x~1)=b1|x~1|12sign(x~1)+b2|x~1|32sign(x~1)μ2(x~1)=b122sign(x~1)+2b1b2x~1+3b222|x~1|2sign(x~1)---(6)]]>其中增益b1,b2>0,此外sign(·)=1,if·≥0-1,if·<0---(7)]]>由式(2)和(5)可得估计误差动态如下x~·1=-c1μ1(x~1)+x~2,x~·2=-c2μ2(x~1)-y··---(8)]]>定理1:如下定义全局李雅普诺夫函数:其中P对称正定矩阵.存在矩阵P＝PT>0,选择合适的参数c1,c2,c3使如下矩阵成立ATP+PA+c3I+4L2CTCPBBTP-1≤0---(10)]]>其中(c1,c2)∈{(c1,c2)∈R2|0<c1<2L,c2>c124+4L2c12}∪{(c1,c2)∈R2|c1>2L,c2>2L},]]>A=-c11-c20,C=10,B=01.]]>那么微分器能够保证状态的准确估计，李雅普诺夫函数的导数满足如下不等式V·1≤-γ1(P,c3,b1)V112(x~)-γ2(P,c3,b2)|x1|12V(x~)---(11)]]>其中γ1(P,c3)和γ2(P,c3)正数且γ1(P,c3)=Δb12c32λmax1/2{P},γ2(P,c3)=Δ3b2c32λmax{P}.]]>这表明式(8)的轨迹曲线开始于初始误差并在有限时间T0内到达原点,T0满足如下不等式T1≤4λmax1/2{P}b12c3V11/2(x~(0))---(12)]]>证明:由于μ2(x~1)=μ1′(x~1)μ1(x~1),μ1′(x~1)=(b12|x~1|1/2+32b2|x~1|12),]]>那么，式(8)可以写成代入由式(13)可得此外,由不等式及那么李雅普诺夫函数满足从式(11)可得，如果则有因此，是有限时间收敛到0的，收敛时间满足式(12)。步骤二(二)、设计基于一致鲁棒精确微分器的全局稳定电机高精度输出反馈控制器如下：定义变量如下：z2=z·1+k1z1=x2-x2eqx2eq=x·1d-k1z1---(15)]]>其中z1＝x1-x1d(t)是输出跟踪误差，k1>0是一个反馈增益。由于G(s)＝z1(s)/z2(s)＝1/(s+k1)是一个稳定的传递函数，当z2趋于0时，z1必然也趋于0。接下来的控制器设计，将以使z2趋于0为主要目标。对式(15)微分并把式(2)代入，可得：z·2=θ1u-θ2x2-x·2eq+d(x,t)---(16)]]>基于估计状态的控制器如下：u＝(ua+us)/θ1n,us＝us1+us2ua=x·^2eq+θ2nx^2---(17)]]>us1=-k2(x^2-x2eq)]]>其中其中k2>0是一个反馈增益。把式(17)代入式(16)，可得z2的动态方程：z·2=-k2(x^2-x2eq)+us2-(θ1n-θ1)u+(θ2n-θ2)x^2+d(x,t)+θ2x~2-k2x~2---(18)]]>由假设1可知，存在Us2满足如下条件：z2us2-(θ1n-θ1)u+(θ2n-θ2)x^2+ks1x~2+θ2x~2-k2x~2+d≤σ1---(19)]]>z2us2≤0其中σ1>0是一个设计参数，在此给出Us2的一个形式：令g为如下函数us2=-ks1z2=Δ-g2z2/(4σ1)---(20)]]>其中θm＝θmax-θmin。由此设计如下的Us2us2=-ks1(x^2-x2eq)=Δ-g2(x^2-x2eq)/(4σ1)---(21)]]>其中ks1为一个非线性增益。步骤三、调节电机控制律u的参数k1，k2，b1，b2，c1，c2使得系统满足控制性能指标。下面结合对前述步骤2所构建系统的稳定性进行验证：定理2：由一致鲁棒精确微分器(9)，设计的基于状态估计的电机输出反馈鲁棒控制器(17)具有如下性质：A.闭环控制器中所有信号均是有界的，定义李雅普诺夫方程V=12z22+12x~22---(22)]]>满足如下的不等式V≤exp(-λt)V(0)+σ1λ[1-exp(-λt)],∀t≥0.---(23)]]>B.如果在某一时刻t0后，系统只存在参数不确定性，即d＝0，当t>max{t0,T0},那么除了A的结论之外，控制器(17)还可以获得渐进跟踪性能，即t→∞时，z2(t)→0，z1(t)→0。证明：对式(22)微分，并把式(18)代入可得V·=z2z·2+x~2x~·2=z2[-k2(x^2-x2eq)+us2-k2x~2-(θ1n-θ1)u+(θ2n-θ2)x^2+d(x,t)+θ2x~2]+x~2x~·2---(24)]]>把式(19)代入式(24)，并根据引理1可得V·≤-λV+σ1---(25)]]>对式(25)两端积分可得不等式(23)。由此可得V全局有界，因此因此z2，z1有界。又因为 系统指令信号均假设有界，由式(12)可知，系统输出信号及x2eq有界，因此控制器u有界。由此证明结论A。下面证明结论B。把式(15)和式(8)代入式(24)，并根据引理1可得V·≤-k2z22=-W---(25)]]>式中W恒为非负，且W∈L2，由式(10)和式(13)可知，有界，因此W是一致连续的，由Barbalat引理，当t→∞时，W→0，由此证明了结论B。因此，控制器是收敛的，系统是稳定的。下面结合一个具体的实例说明上述过程示例性实现。在仿真中取如下参数对系统进行建模：m＝0.01kg·m2，b＝1.25N·s/m，kf＝5N·m/v。经计算可得系统参数的真值为θ1＝500，θ2＝102.5。假设系统参数的界为θmin＝[0,0]T，θmax＝[200,1000]T，给定参数名义值为θ1n＝600,θ2n＝60，系统指令为x1d＝0.2sin(πt)[1-exp(-0.01t3)]rad，仿真步长设为0.5ms。仿真中选取控制器参数为：k1＝100，k2＝650，c1＝5，c2＝5.7。和传统PID控制做对比，经过反复调节，选取PID参数为kp＝90，ki＝70，kd＝0.3。控制律作用效果：结合图2的干扰作用下控制器输入电压u曲线，控制器输入电压满足-10V～+10V的输入范围，符合实际应用。结合图3a-3b所示的状态和其估计状态曲线、图4的指令信号和控制器跟踪误差曲线，可知，本发明提出的控制方法在仿真环境下能够准确的估计出系统状态，本发明设计的控制器能够极大的提高存在干扰情况下系统的控制精度。结果表明在不确定非线性影响下，本发明提出的方法能够满足性能指标。虽然本发明已以较佳实施例揭露如上，然其并非用以限定本发明。本发明所属
技术领域：
中具有通常知识者，在不脱离本发明的精神和范围内，当可作各种的更动与润饰。因此，本发明的保护范围当视权利要求书所界定者为准。当前第1页1 2 3