光伏电站的在线分群等值建模方法与流程

本发明涉及电网分析计算领域，具体涉及一种光伏电站的在线分群等值建模方法。

背景技术：

大规模集中式光伏发电站近年来迅速发展，全球累计光伏装机容量2011年达67GW，2015年就已经达到200GW。大规模大容量的光伏电站接入电网对电网的安全稳定运行产生极大的影响，建立准确的大型光伏电站的动态等值模型成为定量评估大型光伏电站集中接入对电网影响的分析基础，然而大型光伏电站的光伏发电单元数量众多，通常会几十至几百个光伏单元，一般会选自不同厂家的产品，这就造成了不同类型的光伏单元的动态特性存在差异，要想建立这样庞大数量的光伏单元群的整体等值动态模型，难度较大，再加上太阳能是一种波动性能源，不同光照条件下光伏电站的动态特性也会发生改变，这让准确建模变得更加困难。另一方面，为了防止电网故障时光伏电站的脱网造成故障的进一步恶化，以及希望光伏电站能够对故障进行一定程度的支援，低电压穿越(low voltage ride-through,LVRT)能力被作为光伏电站的必备并网指标之一进行考核。《光伏发电站接入电力系统技术规定》(GB/T 19964-2012)对光伏电站的LVRT作出了相应要求，并网点电压跌落时，光伏电站应具备一定的动态无功支撑能力，在保持连接的状态下，还需要向电网输送无功。

现阶段对光伏电站的整体建模，相关技术提出了以特征距离为分群指标的在线分群建模方法,但并未考虑低电压穿越时光伏电站应提供一定的无功支撑所引起的模型变化，不能反映实际运行中的大型光伏电站的特性。

以特征距离为分群指标的在线分群建模方法，虽然将灵敏度转化为离线计算，但考虑到实际大型光伏电站一般含有成百上千个光伏单元，且计算灵敏度时需将输出有功分档，因此灵敏度离线数据库的建立仍计算量较大。

技术实现要素：

本发明旨在至少解决上述技术问题之一。

为此，本发明的一个目的在于提出一种光伏电站的在线分群等值建模方法。

为了实现上述目的，本发明的实施例公开了一种光伏电站的在线分群等值建模方法，包括以下步骤：S1：搭建含有功无功控制环节和低电压穿越控制环节的光伏发电单元模型，进而搭建含有多个光伏单元的光伏电站模型，所述光伏电站模型包括逆变器；S2：根据所述光伏电站模型中各类型的光伏发电单元模型推导计算出模型对应的单位冲激曲线；S3：以所述单位冲激响应曲线的距离为分群指标，利用K-means算法对所述光伏电站模型进行在线分群获得所述逆变器的有功无功控制环节的分群结果；S4：根据所述光伏电站模型中每个光伏单元的实际出力，计算各等值机的等值参数，建立光伏电站的在线分群等值模型。

根据本发明实施例的光伏电站的在线分群等值建模方法，以单位冲激响应曲线的距离为分群指标进行逆变器有功无功控制环节的聚类等值，并与低电压穿越控制环节的等值模型共同构成光伏电站的分群等值模型。该方法的特点是分群结果与光伏单元出力无关，仅由各逆变器控制参数决定，不需要离线建立参数灵敏度数据库，极大地减小了计算量，工程应用更加便利。

另外，根据本发明上述实施例的光伏电站的在线分群等值建模方法，还可以具有如下附加的技术特征：

进一步地，所述光伏电站模型中，所述多个光伏发电单元分别通过多个升压变压器并联于公共连接点，无功补偿为集中电容补偿。

进一步地，步骤S2进一步包括：

通过以下公式得到逆变器控制系统传递函数G(s)：

其中，I_p为光伏单元的有功电流，P_ref为光伏单元的有功功率参考值，K_p为比例常数，K_I为积分常数；

传递函数G(s)的零点z和极点p分别为：

因为U≈1，通过以下公式得到单位冲激响应曲线h(t)：

进一步地，在步骤S3中，设按照等间隔ΔT对单位冲激响应曲线进行抽样，获得的两条单位冲激响应曲线h₁(n)和h₂(n)单位冲激响应曲线的距离L_1-2：

其中，N为总的采样点数。

进一步地，所述利用K-means算法对所述光伏电站模型进行在线分群获得所述逆变器的有功无功控制环节的分群结果进一步包括：

S301：从X中随机选取k个初始聚类中心u₁,u₂,…,u_k，其中，X＝{x₁,x₂,…,x_n}为给定数据集，x_i∈R^m,i＝1,2,…,n，R^m为数据对象是m维向量，给定数据分类数k，将数据对象划分为k个类别，k个类别记为C₁,C₂,…,C_k，每类的聚类中心为u_i，其中n_i是C_i中数据对象的个数；

S302：以u₁,u₂,…,u_k为参照点，对X进行划分，对于数据对象x_p，若||x_p-u_i||<||x_p-u_j||，p＝1,2,…,n,i,j＝1,2,…,k,i≠j则将x_p划分到C_i中；

S303：根据公式重新计算聚类中心u₁^*,u₂^*,…,u_k^*；

S304：若对任意i∈{1,2,…,k}，u_i^*＝u_i都成立，则算法结束；否则，令u_i＝u_i^*，返回S302

S305：输出聚类结果。

进一步地，所述等值参数包括分群模型等值控制参数K_Peq和K_Ieq，分别通过以下公式计算得到：

其中，n为群内光伏单元的数目；P_i为第i个光伏单元的出力。

本发明的附加方面和优点将在下面的描述中部分给出，部分将从下面的描述中变得明显，或通过本发明的实践了解到。

附图说明

本发明的上述和/或附加的方面和优点从结合下面附图对实施例的描述中将变得明显和容易理解，其中：

图1是本发明一个实施例的光伏电站的在线分群等值建模方法的流程图；

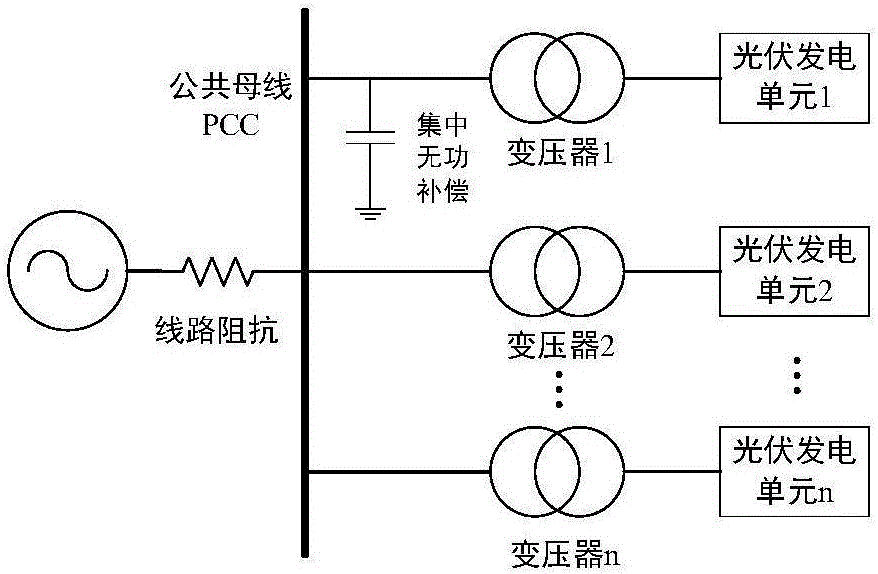
图2是本发明一个实施例的光伏电站的示意图；

图3是本发明一个实施例的光伏发电单元控制框图；

图4是本发明一个实施例的有功无功控制环节框图；

图5是本发明一个实施例的低电压穿越控制环节框图；

图6是本发明一个实施例的有功控制框图。

图7是本发明一个实施例的闭环形式的有功控制框图。

具体实施方式

下面详细描述本发明的实施例，所述实施例的示例在附图中示出，其中自始至终相同或类似的标号表示相同或类似的元件或具有相同或类似功能的元件。下面通过参考附图描述的实施例是示例性的，仅用于解释本发明，而不能理解为对本发明的限制。

在本发明的描述中，需要理解的是，术语“中心”、“纵向”、“横向”、“上”、“下”、“前”、“后”、“左”、“右”、“竖直”、“水平”、“顶”、“底”、“内”、“外”等指示的方位或位置关系为基于附图所示的方位或位置关系，仅是为了便于描述本发明和简化描述，而不是指示或暗示所指的装置或元件必须具有特定的方位、以特定的方位构造和操作，因此不能理解为对本发明的限制。此外，术语“第一”、“第二”仅用于描述目的，而不能理解为指示或暗示相对重要性。

在本发明的描述中，需要说明的是，除非另有明确的规定和限定，术语“安装”、“相连”、“连接”应做广义理解，例如，可以是固定连接，也可以是可拆卸连接，或一体地连接；可以是机械连接，也可以是电连接；可以是直接相连，也可以通过中间媒介间接相连，可以是两个元件内部的连通。对于本领域的普通技术人员而言，可以具体情况理解上述术语在本发明中的具体含义。

参照下面的描述和附图，将清楚本发明的实施例的这些和其他方面。在这些描述和附图中，具体公开了本发明的实施例中的一些特定实施方式，来表示实施本发明的实施例的原理的一些方式，但是应当理解，本发明的实施例的范围不受此限制。相反，本发明的实施例包括落入所附加权利要求书的精神和内涵范围内的所有变化、修改和等同物。

以下结合附图描述本发明。

图1是本发明一个实施例的光伏电站的在线分群等值建模方法的流程图。如图1所示，一种光伏电站的在线分群等值建模方法，包括以下步骤：

S1：搭建含有功无功控制环节和低电压穿越控制环节的光伏发电单元模型，进而搭建含有多个光伏单元的光伏电站模型，光伏电站模型包括逆变器。

在本发明的一个实施例中，光伏电站模型中，多个光伏发电单元分别通过多个升压变压器并联于公共连接点，无功补偿为集中电容补偿。

具体地，如图2所示，光伏电站的系统连接方式如图1，n个光伏发电单元与通过n个升压变压器并联于公共连接点PCC，无功补偿为集中电容补偿。

如图3所示，其中，P_m是光伏阵列的最大有功功率，I_q0为指定的无功电流，光伏单元通过输出电流计算环节这一模块实现与电网的并网接口。

有功无功控制环节、低电压穿越控制环节和输出电流计算环节分别如图4和图5所示，由于在双环控制模式中，内环电流环的响应速度远快于外环电压环，因此可以简化掉电流内环，仅保留外环的PI控制，同时正常运行方式中，无功一般工作在0附近，相对影响较小，因此无功简化为恒定无功电流控制方式，有功、无功电流上下限的计算根据图中式子计算。有功PI控制参数为比例常数K_p和积分常数K_I，n个光伏单元的PI控制参数各不相同。

假设逆变器生产厂家根据国标中规定的最低无功支撑水平来设计低电压穿越控制模型，发生故障时，根据电压跌落程度的不同，该环节提供不同的无功支撑，其中I_N为并网点额定电流。

发电单元输出电流的计算如下式所示：

S2：根据光伏电站模型中各类型的光伏发电单元模型推导计算出模型对应的单位冲激曲线。

具体地，逆变器有功无功控制模型的控制框图如图4所示，忽略测量环节和限幅环节，有功控制框图如图6所示。其中，P为光伏单元发出的有功功率；P_ref为光伏单元的有功功率参考值；I_pout为有功PI调节器的输出。设逆变器的出口电压为U，光伏单元的有功电流为I_p，则稳态时有I_p＝I_pout，P＝U*I_p，有功控制框图可进一步化成图7。以I_p为输出，P_ref为输入，由图6可得逆变器控制系统传递函数G(s)如下：

传递函数G(s)的零点z和极点p分别如下所示：

将传递函数G(s)进一步化简成零极点的形式，如下所示：

由单位冲激响应h(t)和传递函数G(s)间的关系通过以下公式可得h(t)：

忽略掉第一项的冲激函数分量，则

正常情况下，U≈1，因此单位冲激响应h(t)如下所示：

S3：以单位冲激响应曲线的距离为分群指标，利用K-means算法对光伏电站模型进行在线分群获得逆变器的有功无功控制环节的分群结果。

具体地，设按照等间隔ΔT对单位冲激响应曲线进行抽样，获得的离散单位冲激响应曲线为h(n)，则两条单位冲激响应曲线h₁(n)和h₂(n)之间的距离L_1-2定义如下：

其中，N为总的采样点数。

K-means聚类算法适用于处理庞大的样本数据。对于给定的一个数据集X＝{x₁,x₂,…,x_n}，其中，x_i∈R^m,i＝1,2,…,n，即数据对象是m维向量。K-means通过给定数据分类数k，将数据对象划分为k个类别，k个类别记为C₁,C₂,…,C_k。设每类的聚类中心为u_i，其中n_i是C_i中数据对象的个数。选取欧氏距离作为相似性和距离判断准则，计算该类内各点到聚类中心u_i的距离平方和。

聚类目标J(M)为各类总的平方距离和最小。

其中，初始的聚类中心是随机选取的。经过第一次分类后，将聚类中心u_i进行修改得到新的聚类中心并应用于下次分类。

K-means聚类算法的步骤如下：

S301：从X中随机选取k个初始聚类中心u₁,u₂,…,u_k；

S302：以u₁,u₂,…,u_k为参照点，对X进行划分，对于数据对象x_p，若||x_p-u_i||<||x_p-u_j||，p＝1,2,…,n,i,j＝1,2,…,k,i≠j则将x_p划分到C_i中；

S303：根据公式重新计算聚类中心u₁^*,u₂^*,…,u_k^*；

S304：若对任意i∈{1,2,…,k}，u_i^*＝u_i都成立，则算法结束；否则，令u_i＝u_i^*，返回S302；为了防止4中的终止条件不能满足而出现无限循环，通常在算法中设置最大迭代次数；

S305：输出聚类结果。

S4：根据光伏电站模型中每个光伏单元的实际出力，计算各等值机的等值参数，建立光伏电站的在线分群等值模型。

具体地，等值参数包括分群模型等值控制参数K_Peq和K_Ieq，分别通过以下公式计算得到：

其中，n为群内光伏单元的数目；P_i为第i个光伏单元的出力。

低电压穿越控制环节等值参数的计算取出力加权的平均值，如下所示：

其中，K_{q_v(LVRT)}为无功电流与电压之间的比例系数。

逆变器有功无功控制环节的分群模型和低电压穿越控制环节的等值模型共同构成光伏电站的分群等值模型。

另外，本发明实施例的光伏电站的在线分群等值建模方法的其它构成以及作用对于本领域的技术人员而言都是已知的，为了减少冗余，不做赘述。

在本说明书的描述中，参考术语“一个实施例”、“一些实施例”、“示例”、“具体示例”、或“一些示例”等的描述意指结合该实施例或示例描述的具体特征、结构、材料或者特点包含于本发明的至少一个实施例或示例中。在本说明书中，对上述术语的示意性表述不一定指的是相同的实施例或示例。而且，描述的具体特征、结构、材料或者特点可以在任何的一个或多个实施例或示例中以合适的方式结合。

尽管已经示出和描述了本发明的实施例，本领域的普通技术人员可以理解：在不脱离本发明的原理和宗旨的情况下可以对这些实施例进行多种变化、修改、替换和变型，本发明的范围由权利要求及其等同限定。