一种针对三相负载不平衡的无源补偿装置及方法与流程

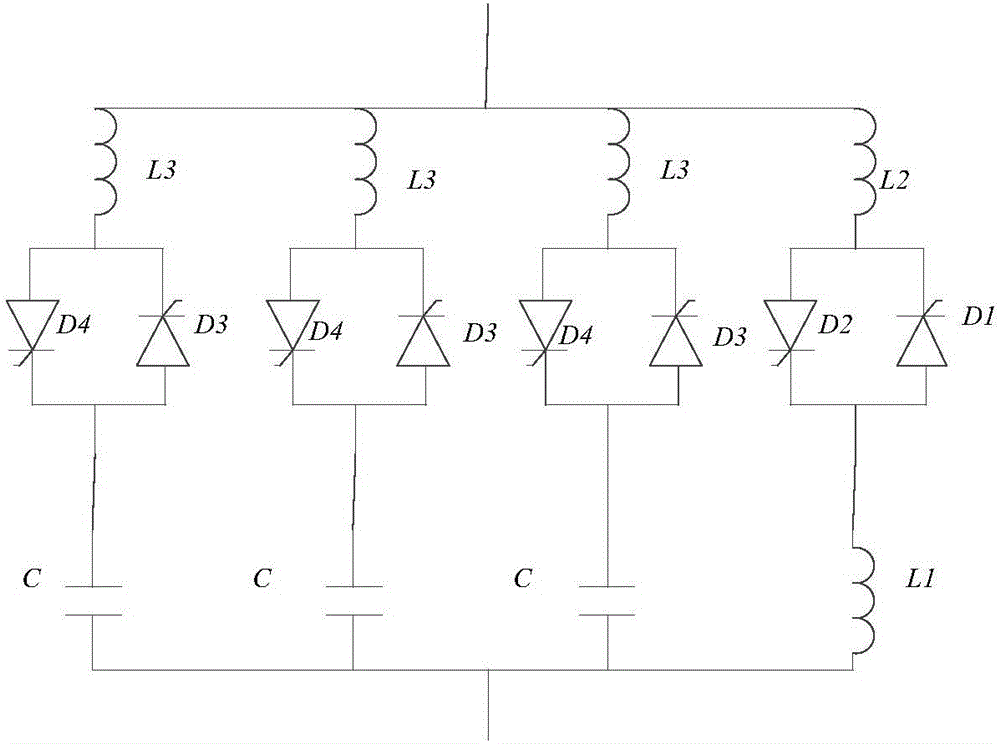
本发明涉及电力
技术领域：
，特别是涉及一种针对三相负载不平衡的无源补偿装置及方法。
背景技术：
：目前，针对电力系统常见的无功不足和负荷三相不对称现象，其补偿装置有通过无源元件补偿和有源元件补偿两种。有源补偿造价高，控制策略复杂，而对于我国乃至国外未来的电力系统而言，无功补偿装置的设备选型问题，技术经济性仍然是一个主要考虑的问题。我国现多采用无源补偿的方式来解决日益严重的三相不平衡现象，也就是静止无功补偿器(SVC)。现有的SVC通常较为复杂，成本较高。另外，现有的SVC利用斯坦米茨理论构造理想的补偿网络，实现分相调节，消除负序电流，平衡三相电网，此理想补偿网络在补偿不平衡负荷带来的不对称电流的同时，要求将功率因数补偿到1，这个约束条件容易导致过补偿的问题。由此可见，在无源补偿中如何降低成本以及克服过补偿的问题是本领域技术人员亟待解决地问题。技术实现要素：本发明的目的是提供一种针对三相负载不平衡的无源补偿装置及方法，用于在无源补偿中如何降低成本以及克服过补偿的问题。为解决上述技术问题，本发明提供一种针对三相负载不平衡的无源补偿装置，包括：并联连接的晶闸管控制电抗器部分和晶闸管投切电容器部分；所述晶闸管控制电抗器部分包括两个第一晶闸管、第二晶闸管和第一电感，所述第一晶闸管和所述第二晶闸管反并联连接，然后与所述第一电感串联连接；所述晶闸管投切电容器部分包括与三相负载连接的3组支路，每组所述支路包括第三晶闸管、第四晶闸管和电容，所述第三晶闸管和所述第四晶闸管反并联连接，然后与所述电容串联连接。优选地，所述晶闸管控制电抗器部分还包括第二电感，所述第二电感的第一端与反并联连接的所述第一晶闸管和所述第二晶闸管连接，所述第二电感的第二端与电网连接。优选地，所述支路还包括第三电感，所述第三电感的第一端与反并联连接的所述第三晶闸管和所述第四晶闸管连接，所述第三电感的第二端与电网连接。为解决上述技术问题，本发明提供一种针对三相负载不平衡的无源补偿方法，基于上述所述的针对三相负载不平衡的无源补偿装置，包括：根据用户的补偿目的选择基于数值逼近的恒功率补偿计算法或恒电流补偿计算法；获取所述恒功率补偿计算法或所述恒电流补偿计算法所需的测量参数；将所述测量参数带入所述恒功率补偿计算法或所述恒电流补偿计算法对应的补偿方程组中；根据当前电网的形态选取所述补偿方程组对应的目标函数；以所述目标函数为依据采用差分进化算法求解所述补偿方程组。优选地，所述补偿方程组为：其中，xqa、xqb以及xqc为三相补偿所需的电抗值；以及为三相补偿电流且满足和分别为AB相的线电压矢量，BC相的线电压矢量。优选地，所述测量参数包括：三相电源电流、AB相的线电压矢量，BC相的线电压矢量、负载功率。优选地，所述以所述目标函数为依据采用差分进化算法求解所述补偿方程组具体包括：S20：输入所述差分进化算法的各计算参数；其中，所述计算参数包括：种群数NP、问题维数D、最大迭代次数tmax；S21：在控制变量的范围内初始化NP个种群，生成初始混沌种群X(0)；其中，所述控制变量包括期望电流、三相电源电流、三相负载电流、三相补偿电流；S22：进行初始计算，对X(0)首次评价得到父代适应度值fit(X(0))；S23：在步骤S22的基础上计算得到子代适应度值U(t)；S24：所述子代适应度值U(t)与其父代适应度值fit(X(0))进行竞争选择，更新最优适应度和种群的全局最优适应度；S25：当所述目标函数适应度小于预定值，对所求得的最优解加一个扰动以进行局部深度搜索；S26：当运行到给定的最大迭代次数tmax时，退出循环，输出最优解，否则返回步骤S23。本发明所提供的针对三相负载不平衡的无源补偿装置，包括：并联连接的晶闸管控制电抗器部分和晶闸管投切电容器部分；晶闸管控制电抗器部分包括两个第一晶闸管、第二晶闸管和第一电感，第一晶闸管和第二晶闸管反并联连接，然后与第一电感串联连接；晶闸管投切电容器部分包括与三相负载连接的3组支路，每组支路包括第三晶闸管、第四晶闸管和电容，第三晶闸管和第四晶闸管反并联连接，然后与电容串联连接。由此可见，本装置具有控制较简单、开发时间短，成本低的优点，在性能和经济上取得了很好的平衡。此外，本发明所提供的针对三相负载不平衡的无源补偿方法，包括：根据用户的补偿目的选择基于数值逼近的恒功率补偿计算法或恒电流补偿计算法；获取恒功率补偿计算法或恒电流补偿计算法所需的测量参数；将测量参数带入恒功率补偿计算法或恒电流补偿计算法对应的补偿方程组中；根据当前电网的形态选取补偿方程组对应的目标函数；以目标函数为依据采用差分进化算法求解补偿方程组。在恒功率补偿计算法和恒电流补偿计算法中采用数值逼近算法和目标函数，不仅可以克服过补偿的问题，而且计算工作量较小。另外，采用数值逼近算法还能掌握运算结果的走向，具有一定的前瞻性。附图说明为了更清楚地说明本发明实施例，下面将对实施例中所需要使用的附图做简单的介绍，显而易见地，下面描述中的附图仅仅是本发明的一些实施例，对于本领域普通技术人员来讲，在不付出创造性劳动的前提下，还可以根据这些附图获得其他的附图。图1为本发明实施例提供的一种针对三相负载不平衡的无源补偿装置的结构图；图2为本发明实施例提供的另一种针对三相负载不平衡的无源补偿装置的结构图；图3为本发明实施例提供的一种恒功率补偿计算法的原理示意图；图4为本发明实施例提供的一种恒电流补偿计算法的原理示意图。具体实施方式下面将结合本发明实施例中的附图，对本发明实施例中的技术方案进行清楚、完整地描述，显然，所描述的实施例仅仅是本发明一部分实施例，而不是全部实施例。基于本发明中的实施例，本领域普通技术人员在没有做出创造性劳动前提下，所获得的所有其他实施例，都属于本发明保护范围。本发明的核心是提供一种针对三相负载不平衡的无源补偿装置及方法。为了使本
技术领域：
的人员更好地理解本发明方案，下面结合附图和具体实施方式对本发明作进一步的详细说明。图1为本发明实施例提供的一种针对三相负载不平衡的无源补偿装置的结构图。如图1所示，针对三相负载不平衡的无源补偿装置包括：并联连接的晶闸管控制电抗器部分和晶闸管投切电容器部分；晶闸管控制电抗器部分包括两个第一晶闸管D1、第二晶闸管D2和第一电感L1，第一晶闸管D1和第二晶闸管D2反并联连接，然后与第一电感L1串联连接；晶闸管投切电容器部分包括与三相负载连接的3组支路，每组支路包括第三晶闸管D3、第四晶闸管D4和电容C，第三晶闸管D3和第四晶闸管D4反并联连接，然后与电容C串联连接。快速响应电网的无功需求，实时进行跟踪补偿是改善电能质量的必要。而电网的三相不平衡度是电能质量的重要指标，三相负载不平衡是电网运行过程中普遍存在的现象，会给用电设备造成不利和损害，严重威胁电网的安全运行。通过幅值和相位均可调节的电流源注入到线路之中，通过电流合成的方法取得线路电流平衡，这种方法一般是通过在线路上并接电容或电感来实现。这一种平衡补偿方法的成本最低，可在配电网中广泛推广应用，但补偿所能取得的效果必须经过最优运算，总体上来讲，单纯采用无功补偿来实现不对称系统的平衡补偿控制，能取得较好的平衡效果，它能借助无功补偿支路等效中性点的偏移改变线路电流的幅值和相位，相当于通过补偿支路并接在线电压或相电压上，使负载电流与补偿电流的合成矢量产生相位偏移，然后再借助于补偿电流的幅值(即改变电抗值的大小)调节，使最终的合成电流基本上满足对称的要求。如图1所示，晶闸管控制电抗器部分采用触发延迟控制方式，通过调整触发延迟角改变系统等效电纳，从而形成连续可调的补偿电抗X。用导通角σ和可调节的电纳B来表示此控制原理：其中，导通角σ与触发延迟角α的关系：α+σ/2＝π；可得：晶闸管控制电抗器部分的需要计算出补偿所需的电抗值X，求倒数得电纳值B，再通过上式求得晶闸管的触发延迟角α，便可转化为晶闸管的触发时间，从而来进行控制，因此，补偿电抗X是计算的重点也是计算的最终目标。通过计算得到的补偿电抗X，就可以计算出晶闸管的触发延迟角α，从而实现补偿的目的。图2为本发明实施例提供的另一种针对三相负载不平衡的无源补偿装置的结构图。在上述实施例的基础上，如图2所示，晶闸管控制电抗器部分还包括第二电感，第二电感的第一端与反并联连接的第一晶闸管和第二晶闸管连接，第二电感的第二端与电网连接。通过加入第二电感，可用来吸收多余的谐波电流并且用来防止电网中出现的冲击电流。在上述实施例的基础上，如图2所示，支路还包括第三电感，第三电感的第一端与反并联连接的第三晶闸管和第四晶闸管连接，第三电感的第二端与电网连接。通过加入第三电感，可用来吸收多余的谐波电流并且用来防止电网中出现的冲击电流。本发明实施例提供的针对三相负载不平衡的无源补偿装置，包括：并联连接的晶闸管控制电抗器部分和晶闸管投切电容器部分；晶闸管控制电抗器部分包括两个第一晶闸管、第二晶闸管和第一电感，第一晶闸管和第二晶闸管反并联连接，然后与第一电感串联连接；晶闸管投切电容器部分包括与三相负载连接的3组支路，每组支路包括第三晶闸管、第四晶闸管和电容，第三晶闸管和第四晶闸管反并联连接，然后与电容串联连接。由此可见，本装置具有控制较简单、开发时间短，成本低的优点，在性能和经济上取得了很好的平衡。现有的SVC利用斯坦米茨理论构造理想的补偿网络，实现分相调节，消除负序电流，平衡三相电网，此理想补偿网络在补偿不平衡负荷带来的不对称电流的同时，要求将功率因数补偿到1，这个约束条件容易导致过补偿的问题。针对上述实施例所述的三相负载不平衡的无源补偿装置，本实施例给出基于该装置的补偿方法，可以克服过补偿的问题。该方法包括：根据用户的补偿目的选择基于数值逼近的恒功率补偿计算法或恒电流补偿计算法；获取恒功率补偿计算法或恒电流补偿计算法所需的测量参数；将测量参数带入恒功率补偿计算法或恒电流补偿计算法对应的补偿方程组中；根据当前电网的形态选取补偿方程组对应的目标函数；以目标函数为依据采用差分进化算法求解补偿方程组。如图1或图2所示，晶闸管控制电抗器部分采用触发延迟控制方式，通过调整触发延迟角改变系统等效电纳，从而形成连续可调的补偿电抗X。用导通角σ和可调节的电纳B来表示此控制原理：其中，导通角σ与触发延迟角α的关系：α+σ/2＝π；可得：晶闸管控制电抗器部分的需要计算出补偿所需的电抗值X，求倒数得电纳值B，再通过上式求得晶闸管的触发延迟角α，便可转化为晶闸管的触发时间，从而来进行控制，因此，补偿电抗X是计算的重点也是计算的最终目标。本实施例中可以采用两种算法，一种是恒功率补偿计算法，另一种是恒电流补偿计算法。在计算过程中，均采用数值逼近算法。恒功率算法是在不考虑线路阻抗的前提下，无论采用什么样的并联平衡补偿方式，电源发出的有功功率在补偿前后都应保持不变，先假设经过平衡补偿后三相电源电流的幅值和相位都完全相同，再计算补偿值的算法。恒电流算法与恒功率算法类似，是假设经补偿后的电源电流幅值保持不变，而相位逐渐增加或减少的数值逼近法。将改进后的差分算法应用于求解恒功率和恒电流提出的问题，在不同补偿方式条件下，选择不同的补偿方式，快速求得相应的补偿电流值，从而计算出所需的补偿电抗值，达到平衡补偿的目的。1、恒功率补偿计算法在不考虑线路阻抗的前提下，无论采用什么样的并联平衡补偿方式，电源发出的有功功率在补偿前后都应保持不变。换句话说，系统不能因为实施了平衡补偿措施而使负载应得到的有功功率变少或变多了。提供的为本发明实施例的一种恒功率补偿计算法的原理示意图。如图3所示，根据恒功率这一要求，在具体计算过程中，可以首先假设经过平衡补偿后三相电源电流的幅值和相位都完全相同，因此，期望电流值Ids应满足补偿前后的有功功率相同，即PL＝P＝3Ids·U，由此可推得期望电流值：Ids=PL3U---(1)]]>式中“U”为电源相电压有效值；“PL”为负载有功功率，即补偿前的有功功率；“P”为补偿后的有功功率。根据能量守恒的原则，补偿后三相电源电流Ik(k＝a、b、c)的矢量终点都必须落在图3所示的“补偿电流矢量终点轨迹”的直线上，且合成补偿电流矢量的终点只有在这条直线上的移动才能保证平衡补偿前后的有功功率不变，因在对应直线上移动的每相合成电流矢量在对应电压矢量上的投影始终保持不变，即有功电流分量保持不变。在电力系统的实际运行中要求所采取的任何补偿措施，都不允许出现过补现象，因此，平衡补偿后的系统电流都应保证系统的功率因数为滞后特性，因而数值逼近的移动轨迹也应按照图示的虚线方向移动。由图3的矢量图知，各相补偿电流可以表示为：I·qa=I·a-I·LaI·qb=I·b-I·LbI·qc=I·c-I·Lc---(2)]]>其中，分别为各相负载电流，分别为三相电源电流；一般情况下，总是先假设电源电流的幅值等于式(1)计算得到的期望电流Ids，初始相位设定为与各对应相电压的矢量方向相同。由于负载电流为已知量，因此，三相补偿电流矢量可根据假设已知的三相电源电流进行计算。其中，补偿电流应满足基尔霍夫电流定律的约束条件，即I·qa+I·qb+I·qc=0---(3)]]>在一般情况下，这种由假设线路电流推得的补偿电流很难同时满足式(2)和式(3)，此时就应该使线电流沿着虚线的滞后方向逐渐移动，当然，补偿电流也随之改变，直至满足要求或达到一定的精度要求为止。在这种数值逼近的过程中，如果存在某一点能够同时满足式(2)和式(3)的要求，则可继续求解各补偿支路的参数。由于各相补偿电纳与各相电压之间存在关系：其中，Bqk(k＝a,b,c)为补偿电纳值，UNq为补偿支路中心点电位。令U·Nq=YqaU·a+YqbU·b+YqcU·cYqa+Yqb+Yqc---(5)]]>其中，Yqk(k＝a，b，c)为各补偿支路的导纳值(Y＝G+jB，我们采取的电容电感式的无源补偿方式，只有B没有G，所以此处Yqk＝Bqk)，考虑到式(4)中三个表达式的补偿中性点电压矢量必定是相同的，即UNq相等，将式(5)式代入(5.4)式可推得补偿电抗值，即补偿方程组：其中，xqa、xqb以及xqc为三相补偿所需的电抗值；和分别为AB相的线电压矢量，BC相的线电压矢量。只要在上式中令xqc＝1/Bqc为某一个合适的数值，就可以顺次求得xqb和xqa的值，进而通过式(5)求得补偿结构中性点的电压矢量。显然，满足式(6)的补偿电抗值有很多组合，它是一个线性集合，应在其中选择一组最优组合。由以上数值逼近的过程可以看出，关键的是沿着恒功率补偿轨迹找到一个点，使之能同时满足式(4)和式(6)的条件。在计算工作点逐渐移动的过程中，不仅线路电流的幅值会逐渐增加，而且相位的滞后也越来越大。如果在逼近过程中始终不能找到一个满足精度要求的工作点，则只能在相反方向再进行同样的搜寻工作。若双向搜寻都得不到满意的结果，就只能在已搜寻的结果中找出偏差最小的一组数据，这组数据也就是能量守恒所能得到的最佳结果。另一个应注意的是，应对搜寻移动计算中拟设定的线电流幅值和相位有一个限制，否则可能会陷入无穷搜寻而无法收敛的死循环之中。此外，如果所得最优解为超前功率因数，则必须另外增加一套三相感性对称补偿，以校正超前功率因数的过补问题。2、恒电流补偿计算法恒电流计算法与上述恒功率计算法的基本计算原则是相同的，只是在恒电流计算法中是假设经补偿后的电源电流幅值保持不变，而相位逐渐增加或减少的数值逼近法。图4为本发明实施例提供的一种恒电流补偿计算法的原理示意图。如图4所示，圆形轨迹即为三相电流数值逼近的移动轨迹。由图可见，在任何时候，补偿后的线电流幅值始终保持不变，只是通过相位的移动来尝试补偿电流能否满足平衡要求。与恒功率计算的过程相似，它们都是假设经过平衡补偿后的电源电流为某一对称电流，然后再根据已知的负载电流与假设的平衡电流之差得到各补偿支路应提供的补偿电流矢量。只要补偿电流满足式(2)和式(3)的要求，则表明确实存在一组三相补偿电流能够满足平衡补偿的要求。只是此处的尝试工作点是沿着圆弧移动，而恒功率计算的尝试工作点是沿着直线移动。但在恒电流计算中，平衡工作点的电流选择原则与恒功率计算的选择原则却完全不同，此处是以满足负载最小容量SL作为尝试电流(尝试电流即为假设的一个期望电流)的选择的约束条件。具体的初始期望计算电流幅值可定为：Ids=SL3U---(7)]]>计算的初始工作点可先假设经补偿后的三相功率因数均为“1”，然后逐渐向顺时针方向移动。此时，期望的电流幅值应以三相负载的总容量作为参考依据，其目的是使补偿后的电源电流幅值能够在满足负载容量的前提下达到最小值。按式(1)所选定的初始电流幅值是平衡后可能得到的最小电流幅值，如果能得到满足要求的最优解，就应该是全局最优解。否则，就应适当增加一个步长，使Ids＝Ids0+ΔI，重新沿着较大的圆弧轨迹实施数值逼近的运算，直至得到满足要求的解。此处，Ids0为前一次的计算值，ΔI为电流增量。在实际计算中，所假设的补偿后的平衡电流相位应控制在±90°的范围以内，而且也应先进行滞后功率因数的平衡尝试。在滞后功率因数无法取得满意效果时，才能再进行超前功率因数的平衡尝试，直至得到满足结果为止。角度的增量不能太大，一般可选择在1％度左右(角度的增量即为补偿后的平衡电流相位)。若仍不能得到满足效果，则应增加平衡电流的幅值，使Ids＝Ids0+ΔI在新的幅值下重新进行运算。幅值增量ΔI越小，精度会越高，一般可定为式(1)结果的1/105，但Ids的最大值尝试值也不应达到式(7)结果的两倍，否则，平衡后的线路电流就会很大，从而造成平衡后的系统功率因数太低。应特别注意的是，根据恒功率补偿计算法和恒电流补偿计算法两种不同方式进行数值逼近运算时，可能会得到不同的最优补偿结果，这与不同计算方法的步长增量有关。如果两个结果存在较大的差异，则说明满足平衡补偿条件的解有很多，但这并不会影响两个结果的正确性。如果确实存在很多解，则应在解的集合中寻找一个最优解，本实施例不再赘述。在求解式(7)对应的方程组时，需要设定一个目标函数即约束条件，对于目标函数的选取适当与否，直接关系到后续差分进化算法中种群中个体优劣的判断标准。根据不同的评价要求，其目标函数也有所不同。本实施例中目标函数的选取除了考虑系统平衡补偿以外，还考虑了节能方面的问题。为了合理补偿不对称电力系统问题，以下根据当前电网的形态(三相四线制和三相三线制)，分为两种不同的目标函数加以说明。在三相四线制平衡补偿计算系统中，△型补偿采用数值逼近的计算方法，目标函数是式：其中，(k＝a、b、c)为实际可能得到的各相功率因数角的最优计算值，为经过平衡补偿后所期望的最优功率因数角，一般同时还要求值越小越好。yk(k＝a、b、c)为经最优计算后得到的三相最优导纳的幅值，yds为补偿后希望获得的各相最优导纳幅值。求得的参数不仅使三相电流的幅值基本相同，而且还能使三个电流之间的相位差非常接近120°，从而达到不对称系统平衡补偿的目的。同时考虑到节能问题(算法需要多个目标函数作为约束条件来寻优)，所以选的另一个目标函数是使补偿值尽可能小，在△型补偿时，节能目标函数为：Iq＝min[Iqa+Iqb+Iqc](9)其中Iq为各补偿支路电流之和，Ik(k＝a,b,c)为各补偿支路电流。在三相三线制平衡补偿计算系统中，最优平衡补偿目标为式：ei=f(Bqab,Bqbc,Bqca)=min((Ia-Ids)2+(Ib-Ids)2+(Ic-Ids)2)eφ=φ(Bqab,Bqbc,Bqca)=min((φa-φds)2+(φb-φds)2+(φc-φds)2)---(10)]]>其中，Ik为经最优计算后得到的三相最优电流的幅值，Ids为补偿后希望获得的各相最优电流幅值；为期望的功率因数角。采取Y型补偿时，节能目标函数为：I′q＝min[Iqa+Iqb+Iqc](11)最终的结果应满足无功电流或综合电纳最小方差的值的选取原则，即：min(ΔI)=min(Iaj2+Ibj2+Icj2)min(Δy)=min(Ba2+Bb2+Bc2)---(12)]]>优化问题的目标函数规定为优化到最小，因此相应的目标函数值越小越好。在上述实施例的基础上，所述测量参数包括：三相电源电流、AB相的线电压矢量，BC相的线电压矢量、负载功率。其中，负载功率包括负载有功功率和负载无功功率。在上述实施例的基础上，以目标函数为依据采用差分进化算法求解补偿方程组具体包括：S20：输入差分进化算法的各计算参数；其中，计算参数包括：种群数NP、问题维数D、最大迭代次数tmax；其中，所述控制变量包括期望电流、三相电源电流、三相负载电流、三相补偿电流；S21：在控制变量的范围内初始化NP个种群，生成初始混沌种群X(0)；S22：进行初始计算，对X(0)首次评价得到父代适应度值fit(X(0))；S23：在步骤S22的基础上计算得到子代适应度值U(t)。S24：子代适应度值U(t)与其父代适应度值fit(X(0))进行竞争选择，更新最优适应度和种群的全局最优适应度；S25：当目标函数适应度小于预定值，对所求得的最优解加一个扰动以进行局部深度搜索；S26：当运行到给定的最大迭代次数tmax时，退出循环，输出最优解，否则返回步骤S23。可以理解的是，差分进化算法的原理为本领域技术人员所熟知，本实施例不再赘述。最大迭代次数可以根据实际情况设定，本实施例也不再赘述。本实施例提供的针对三相负载不平衡的无源补偿方法，包括：根据用户的补偿目的选择基于数值逼近的恒功率补偿计算法或恒电流补偿计算法；获取恒功率补偿计算法或恒电流补偿计算法所需的测量参数；将测量参数带入恒功率补偿计算法或恒电流补偿计算法对应的补偿方程组中；根据当前电网的形态选取补偿方程组对应的目标函数；以目标函数为依据采用差分进化算法求解补偿方程组。在恒功率补偿计算法和恒电流补偿计算法中采用数值逼近算法和目标函数，不仅可以克服过补偿的问题，而且计算工作量较小。此外，采用数值逼近算法还能掌握运算结果的走向，具有一定的前瞻性。以上对本发明所提供的针对三相负载不平衡的无源补偿装置及方法进行了详细介绍。说明书中各个实施例采用递进的方式描述，每个实施例重点说明的都是与其他实施例的不同之处，各个实施例之间相同相似部分互相参见即可。对于实施例公开的装置而言，由于其与实施例公开的方法相对应，所以描述的比较简单，相关之处参见方法部分说明即可。应当指出，对于本
技术领域：
的普通技术人员来说，在不脱离本发明原理的前提下，还可以对本发明进行若干改进和修饰，这些改进和修饰也落入本发明权利要求的保护范围内。专业人员还可以进一步意识到，结合本文中所公开的实施例描述的各示例的单元及算法步骤，能够以电子硬件、计算机软件或者二者的结合来实现，为了清楚地说明硬件和软件的可互换性，在上述说明中已经按照功能一般性地描述了各示例的组成及步骤。这些功能究竟以硬件还是软件方式来执行，取决于技术方案的特定应用和设计约束条件。专业技术人员可以对每个特定的应用来使用不同方法来实现所描述的功能，但是这种实现不应认为超出本发明的范围。结合本文中所公开的实施例描述的方法或算法的步骤可以直接用硬件、处理器执行的软件模块，或者二者的结合来实施。软件模块可以置于随机存储器(RAM)、内存、只读存储器(ROM)、电可编程ROM、电可擦除可编程ROM、寄存器、硬盘、可移动磁盘、CD-ROM、或
技术领域：
内所公知的任意其它形式的存储介质中。当前第1页1 2 3