计及电压稳定约束的微电网潮流优化方法与流程

本发明涉及一种微电网的潮流优化方法，尤其涉及一种考虑电压稳定约束的微电网潮流优化方法。

背景技术：

最优潮流(Optimal Power Flow,OPF)是电力系统运行和控制的重要手段之一，也是电能管理系统的重要组成部分。所谓的最优潮流，就是当电力系统的结构参数及负荷情况给定时，通过控制变量的优选，找到能满足所有指定的约束条件，并使系统的一个或多个性能指标达到最优时的潮流分布。随着智能电网建设的不断推进，清洁高效的可再生能源发电技术受到了广泛的关注，近些年来，由各种分布式电源(Distributed Generation,DG)、分布式储能单元(Storage Unit,SU)、负荷以及监控和保护装置集合成的微电网系统在电力系统中的渗透率不断提高，其扮演的角色越来越突出。微电网中光伏、风电等分布式电源具有很强的间歇性，严重影响了系统的安全运行。相关研究表明，电压稳定性是微电网并网运行所需要考虑的一个重要安全因素。就微电网的运行优化问题而言，通常可以用网络优化后的经济性、安全性等指标来衡量优化方案的优劣，而这些指标与微电网中的DG和SU的运行状态密切相关。因此，在DG和SU大量渗透的微电网中，亟需重新设计微电网的合适的运行指标、优化数学模型和相应的求解算法。

目前国内外现有的潮流优化方法难以很好地满足微电网发展和建设的需要，主要表现在：

1.多数潮流优化模型未能充分计及分布式电源和储能单元的影响。虽然已出现了一些计及DG影响的潮流优化方法，但对DG的建模尚显粗糙，一般是将DG视为普通电源或“负的负荷”进行处理，而未进行分类等值，同时尚缺少对SU的科学建模。

2.微电网并网运行时电压稳定性受间歇性微源的影响较大，虽然已出现了一些计及电压稳定性约束的潮流优化方法，但传统的电压稳定性指标未能充分考虑微电网的并网运行特性及DG、SU的作用，从而不能对电压稳定性做更好的评估。

3.微电网具有明显的三相不平衡特征，在计算优化方案的网损和电压等指标时，已有的很多优化方法未能充分考虑微电网三相参数和负荷的不平衡性，从而影响计算精度。

4.微电网优化模型具有连续变量和离散变量共存的特点，传统数学规划法处理离散变量较困难，且全局寻优能力不强；现有的智能算法计算速度慢，且易陷入局部最优。

技术实现要素：

本发明的目的就是为了解决上述问题，提出了一种计及电压稳定约束的微电网潮流优化方法,该方法具有计及电压稳定性、优化模型更精确、计算速度更快、全局寻优效率更高等优点。

为实现上述目的，本发明的具体方案如下：

一种计及电压稳定约束的微电网潮流优化方法，包括以下步骤：

步骤一：结合微电网的并网运行特性，建立电压稳定性指标；

步骤二；分别以微电网网络有功损耗最小和负荷均衡度最高为优化目标，建立微电网优化的数学模型；

步骤三：确定微电网优化数学模型的约束条件，包括：功率平衡约束、节点电压约束、无功补偿电容器补偿约束、变压器容量约束、DG的注入功率约束、SU的功率B_i和能量S_i约束以及电压稳定约束；

步骤四：对微电网优化案例中的离散控制变量采用历史拟合法处理，得到连续的最优目标变量；

步骤五：基于预测-校正内点法，通过引入最优目标变量，利用AMD算法进行节点优化编号，构造出计及电压稳定性约束的历史拟合预测-校正内点法，对微电网优化案例进行最优潮流计算，获取电压稳定性指标，并将计算得到的电压稳定性指标再反馈到历史拟合预测-校正内点法进行优化处理，得到微电网优化数学模型的最优解。

进一步地，对含有分布式电源和储能单元高渗透率的微电网系统，利用三相前推回代潮流算法将弱环网转化为辐射型网络，通过在断点两侧注入补偿量的方法来等效微电网所含的环路的影响；同时根据各类分布式电源与电网互联的接口方式以及它们的运行和控制方式，分别建立其在潮流计算中的等值模型，在各迭代步将分布式电源所在节点转换为PQ节点、PI节点或PV节点。

进一步地，对含有分布式电源和储能单元高渗透率的微电网系统，潮流计算的具体方法为：

(1)对微电网的原始数据进行初始化，包括微网拓扑信息、元件参数、负荷数据；

(2)形成回路阻抗矩阵Z；

(3)计算各负荷节点的注入电流；

(4)确定分布式电源和储能单元的等值注入电流；

(5)判断网络中是否存在环网回路，若存在环网回路则向解环节点叠加注入电流；

(6)叠加储能单元及分布式电源的三相注入电流，进行三相前推回推潮流计算；

(7)从馈线末端节点开始进行前推计算，对支路电流进行求和，从而得到各条支路始端节点的三相电流；

(8)从馈线首端节点开始回推计算各支路末端节点的电压，同时对各节点的三相电压进行修正；

(9)修正PV节点注入的无功功率，然后判断PV节点的无功功率是否发生越界，若发生越界则将PV节点转化成PQ节点转入步骤(3)重新进行计算，否则转入(10)；

(10)以节点相邻两次迭代电压幅值差是否满足预设精度为收敛条件，若满足条件则迭代收敛，转入(11)，否则重新修正所在节点的注入电流，然后转入步骤(3)重新计算；

(11)计算结束，输出潮流计算结果。

进一步地，所述步骤一中，电压稳定性指标L_mg具体为：

其中，为连有DG节点的电压相量；为连有SU节点的电压相量，为负荷节点电压相量；F_ij为负荷参与因子；S_G为连有DG节点的集合；S_S为连有SU节点的集合；S_L为全部负荷节点的集合。

进一步地，所述步骤二中，建立的微电网优化的数学模型具体为：

其中，f₁为网络有功损耗；f₂为支路最大负荷率；M＝{A,B,C}为相序集合；B为微电网所有支路集合；P_ij.m、Q_ij.m和I_ij.m分别为流过支路ij的有功功率、无功功率和电流；R_ij.m为支路ij的电阻；V_ij.m为支路ij的末端电压；I_N.ij.m为支路ij的额定电流。

进一步地，所述步骤三中，

(1)功率平衡约束具体为：

对微电网中任一节点i，需满足如下条件：

其中，P_i和Q_i分别为节点i的注入有功功率和无功功率；P_loss、Q_loss分别为微电网的有功损耗和无功损耗；V_i和V_j分别为节点i和节点j的电压幅值；G_ij和B_ij分别为支路导纳Y_ij的虚部与实部；θ_ij为节点i与节点j的相角差；N为微电网节点集合；

(2)节点电压约束具体为：

V_i.min≤V_i≤V_i.max i∈N；

其中，V_i.min和V_i.max分别为节点i的电压下限和上限；V_i为节点的电压；

(3)无功补偿电容器补偿约束具体为：

Q_cri.min≤Q_cri≤Q_cri.max i∈N_C；

其中，Q_cri为无功补偿电容器的无功补偿量；Q_cri.max、Q_cri.min为补偿量Q_cri的上下限；N_C为无功补偿节点集合。

进一步地，所述步骤三中，

(1)DG的注入功率约束具体为：

P_Gi.min≤P_Gi≤P_Gi.max i∈G_P；

Q_Gi.min≤Q_Gi≤Q_Gi.max i∈G_Q；

其中，P_Gi和Q_Gi分别为第i个DG的有功和无功输出；P_Gi.max和P_Gi.min分别为其对应的有功功率上、下限；Q_Gi.max和Q_Gi.min分别为其对应的无功功率上、下限；G_P和G_Q分别为有功可调和无功可调的可控DG集合；

(2)SU的功率B_i和能量S_i约束具体为：

P_charge≤B_i≤P_discharge i∈N；

S_low≤S_i≤S_high i∈N；

其中，P_discharge为SU最大放电功率；P_charge为SU最大充电功率；S_low为SU的最小剩余能量，S_high为SU的最大剩余能量；

(3)电压稳定约束条件具体为：

L_mgi.min≤L_mgi≤L_mgi.max i∈N；

其中，L_mg为电压稳定性指标，L_mgi.max和L_mgi.min分别为L_mgi的上下限。

进一步地，所述步骤四的具体方法为：

(4-1)选择要调整的离散控制变量，确定所述离散控制变量在微电网中的位置；

(4-2)设定参数调整方法，进行自动历史拟合；

(4-3)数据分析，如果数据分析结果不合理，则返回循环的起点，选择其他调整区域、改变调整的参数或修改参数的采样范围；如果结果合理，且参数收敛到特定数值，则进入下一步；

(4-4)将最优结果拟合起来，得到一个连续的最优目标变量。

进一步地，所述步骤五的具体方法为：

(5-1)数据初始化，读入微电网的基础参数和运行数据，同时给定原始变量与对偶变量的初值，并保证松弛变量u、l≥0，拉格朗日乘子y≠0、z≥0、w≥0，障碍因子μ≥0，设置初始迭代次数k＝0、最大迭代次数K_max、收敛标准差ε₁、ε₂；

(5-2)判断所需调整控制变量是否为离散变量；若是离散变量，则对其进行历史拟合为连续的最优目标变量，然后转入(5-3)，若为连续变量，则直接转入(5-3)；

(5-3)利用AMD算法根据节点度的上限值来选择要编号节点原理，对改进内点法修正方程的系数矩阵进行节点优化编号；

(5-4)计算互补间隙Gap与K-T条件的最大范数F_max＝max{||L_x||，||L_y||，||L_z||，||L_w||}；

(5-5)判断Gap＜ε₁且F_max＜ε₂是否成立，不成立直接转入(5-6)，若成立则输出最优解结束计算；

(5-6)计算各类函数的雅各比矩阵与海森矩阵

(5-7)求解仿射方程原变量及对偶变量的仿射步长及放射方向下的互补间隙Gap^Aff；

(5-8)根据预测中心参数σ＝(Gap^Aff/Gap)³，计算障碍因子μ；

(5-9)求解迭代方程，得到迭代方向Δx、Δy、Δu、Δw、Δl、Δz；

(5-10)求解原始变量与对偶变量的迭代步长step_d、step_d，更新原始变量与对偶变量；

(5-11)判断当前迭代次数k是否小于最大迭代次数k_max，若满足则置k＝k+1并转入(5-4)，不满足则“输出计算不收敛”并终止计算。

本发明的有益效果：

1.所建立的电压稳定性指标能更有效地评估微电网系统各节点的电压稳定性。

2.所构建的多目标多约束优化模型能够同时计及分布式电源和储能单元的影响。

3.所采用的多电源三相前推回代算法能够很好地考虑微电网的三相不平衡特征，且计算速度快；

4.所采用的历史拟合预测-校正内点法能对离散控制变量进行更好的处理，解决了计算精度与迭代效率之间的矛盾，具有更好的全局寻优特点，并保持了预测-校正内点法优点。

附图说明

图1为微电网潮流优化的总体设计图；

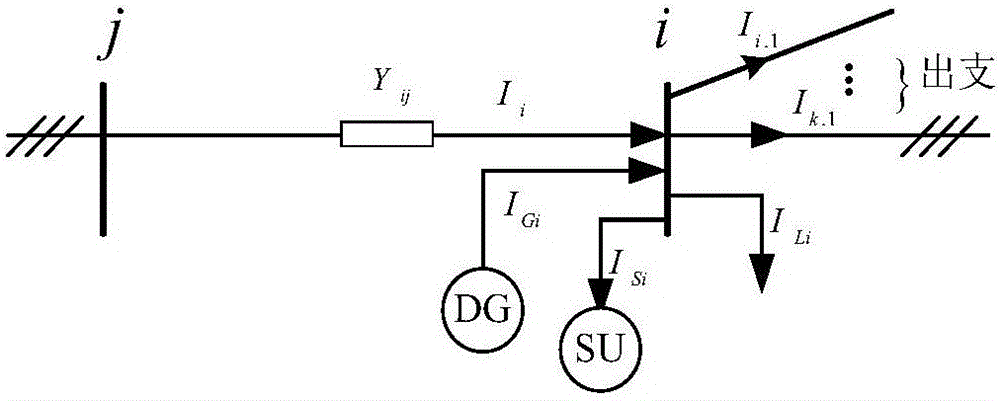
图2为馈线模型；

图3为微电网三相潮流计算流程图；

图4为离散控制变量历史拟合流程图。

图5为历史拟合预测-校正内点法流程图。

具体实施方式：

下面结合附图对本发明进行详细说明：

计及电压稳定约束的微电网潮流优化方法，它的具体步骤是：如图1所示，首先结合微电网的并网运行特性，建立电压稳定性指标L_mg；然后计及分布式电源与储能单元的影响建立微电网的多目标、多约束优化数学模型；基于预测-校正内点法通过引入历史拟合得到的连续的最优目标变量和利用AMD算法进行节点优化编号，构造出计及电压稳定性约束的历史拟合预测-校正内点法；解算过程中反复调用三相潮流计算模块对微电网优化方案进行三相潮流计算，进而得到的电压稳定性指标L_mg，再反馈到历史拟合预测-校正内点法进行优化处理。

图2为馈线模型，其中，I_i为支路ij向节点i的注入电流，Y_ij为支路ij的导纳，I_Li为节点i的负荷端注入电流，I_Gi和I_Si分别为节点i所接DG的注入电流和SU的充放电电流，I_i.1和I_i.k分别为节点i的第1出支和第k出支的输出电流。

下面对本发明方法进行详细的说明：

1.建立适合微电网并网运行特性的电压稳定性指标L_mg：

式中：为连有DG节点的电压相量；为连有SU节点的电压相量，为负荷节点电压相量；F_ij为负荷参与因子；S_G为连有DG节点的集合；S_S为连有SU节点的集合；S_L为全部负荷节点的集合。

2.建立微电网优化的数学模型，模型中的目标函数有两个，分别为微电网网络有功损耗最小和负荷均衡度最高，表达式为：

式中：f₁为网络有功损耗；f₂为支路最大负荷率；M＝{A,B,C}为相序集合；B为微电网所有支路集合；P_ij.m、Q_ij.m和I_ij.m分别为流过支路ij的有功功率、无功功率和电流；R_ij.m为支路ij的电阻；V_ij.m为支路ij的末端电压；I_N.ij.m为支路ij的额定电流。

微电网优化数学模型的约束条件包括：

1)功率平衡约束，对微电网中任一节点i，需满足如下条件：

式中：P_i和Q_i分别为节点i的注入有功功率和无功功率；P_loss、Q_loss分别为微电网的有功损耗和无功损耗；V_i和V_j分别为节点i和节点j的电压幅值；G_ij和B_ij分别为支路导纳Y_ij的虚部与实部；θ_ij为节点i与节点j的相角差；N为微电网节点集合。

2)节点电压约束，即各节点的电压V_i应满足：

V_i.min≤V_i≤V_i.max i∈N (6)

式中：V_i.min和V_i.max分别为节点i的电压下限和上限。

3)无功补偿电容器补偿约束：

Q_cri.min≤Q_cri≤Q_cri.max i∈N_C (7)

式中：Q_cri为无功补偿电容器的无功补偿量；Q_cri.max、Q_cri.min为补偿量Q_cri的上下限；N_C为无功补偿节点数。

4)变压器容量约束：

|S_t|≤S_N.t t∈T (8)

式中：S_t和S_N.t分别为变压器t的实际功率和额定容量；T为所有变压器的集合。

5)DG的注入功率约束为：

P_Gi.min≤P_Gi≤P_Gi.max i∈G_P (9)

Q_Gi.min≤Q_Gi≤Q_Gi.max i∈G_Q (10)

式中：P_Gi和Q_Gi分别为第i个DG的有功和无功输出；P_Gi.max和P_Gi.min分别为其对应的有功功率上、下限；Q_Gi.max和Q_Gi.min分别为其对应的无功功率上、下限；G_P和G_Q分别为有功可调和无功可调的可控DG集合。

6)SU的功率B_i和能量S_i约束，即优化模型需满足SU运行的功率和能量等物理限制：

P_charge≤B_i≤P_discharge i∈N-1 (11)

S_low≤S_i≤S_high i∈N (12)

式中：P_discharge为SU最大放电功率(正数)；P_charge为SU最大充电功率(负数)；S_low为SU的最小剩余能量，S_high为SU的最大剩余能量。

7)电压稳定约束条件，基于式(1)中建立的电压稳定性指标L_mg，将微电网并网运行应满足的电压稳定性约束条件表示为：

L_mgi.min≤L_mgi≤L_mgi.max i∈N (13)

式中：L_mgi.max和L_mgi.min分别为L_mgi的上下限；L_mgi指标的取值范围为0～1，当该指标接近0时，表示电压稳定性较好，而当指标接近于1时，系统运行点将接近电压崩溃点。因此全局电压稳定的条件是所有负荷点计算出来的指标均小于1。

3.针对DG和SU高渗透率的微电网，设计三相前推回代潮流算法。

流程图如图3所示，对DG和SU的高渗透率的微电网络优化方案，采用前推回代算法计算系统潮流，鉴于该算法对网孔的处理能力较弱，本模块对前推回代法进行改进，将弱环网转化为辐射型网络，通过在断点两侧注入补偿量的方法来等效环路的影响。此外，根据各类分布式电源(风电、光伏、燃料电池，微型燃气轮机等)与电网互联的接口方式以及它们的运行和控制方式，分别建立其在潮流计算中的等值模型，在各迭代步将分布式电源所在节点转换为PQ节点、PI节点或PV节点。在计算过程中，各元件均采用模型库中的三相模型参与计算。具体方法为：

(1)首先进行微电网数据初始化，读取系统网络参数和负荷参数；

(2)形成回路(环路)阻抗矩阵Z；

(3)根据读入的数据计算各负荷节点的注入电流；

(4)按如下方式计算DG及SU的等值注入电流：

对第i个DG，其第m相的注入电流相量表示为：

式中：G_PQ为功率给定的DG(即PQ型)所构成的集合；G_PV为有功和电压幅值给定的DG(即PV型)所构成的集合；G_PI为有功和电流幅值给定的DG(即PI型)所构成的集合；P_gi.m、Q_gi.m、和分别为第i个DG的第m相的有功功率、无功功率和端电压；为PV型DG的节点解算电压与给定电压的差值；Z_i.m为PV型DG与源节点相连的支路阻抗之和；I_gi0.m为PI型DG的第m相的给定电流；

对第j个SU，其第m相的注入电流幅值I_j.m表示为：

式中：S_I和S_V分别为按恒流方式和按恒压方式储能的SU所构成的集合；I_0.j为储能单元的给定充电电流；V_j.m和E_j.m分别为储能单元j的第m相的充电电压和内电势；R_j为储能单元j的充电回路电阻。

(5)判断网络中是否存在环网回路，若存在环网回路则向解环节点叠加注入电流；

(6)叠加DG及SU的三相注入电流，进行三相前推回推潮流计算；

(7)从馈线末端节点开始进行前推计算，对支路电流进行求和，从而得到各条支路始端节点的三相电流；

(8)从馈线首端节点开始回推计算各支路末端节点的电压，同时对各节点的三相电压进行修正；

(9)修正PV节点注入的无功功率，然后判断PV节点的无功功率是否发生越界，若发生越界则将PV节点转化成PQ节点转入步骤(3)重新进行计算，否则转入(10)；

(10)以节点相邻两次迭代电压幅值差是否满足预设精度为收敛条件，若满足条件则迭代收敛，转入(11)，否则重新修正所在节点的注入电流，然后转入步骤(3)重新计算；

(11)计算结束，输出潮流计算结果。

4.对微电网优化案例中的离散控制变量采用历史拟合法处理，得到连续的目标变量。流程图如图4所示。具体步骤包括：

(1)选择要调整的离散控制变量，另外了解其在微电网中的位置及如何对这些变量进行调整；

(2)选择参数调整方法，本发明选取邻域法(一种随机采样算法)；

(3)自动历史拟合(对比观测数据与预测数据，计算不吻合值，控制更新参数，直至数据吻合为止)；

(4)数据分析，如果数据分析结果不合理，则返回循环的起点，选择其他调整区域、改变调整的参数或修改参数的采样范围；如果结果合理，且参数收敛到特定数值，则转步骤(5)。

(5)将最优结果拟合起来，得到一个连续的最优目标变量。

5.基于预测-校正内点法，通过引入历史拟合得到的连续的最优目标变量和利用AMD算法进行节点优化编号，以提高算法的收敛速度与全局寻优性，将该算法用于求解微电网的最优潮流问题。流程图如图5所示。具体步骤包括：

(1)数据初始化，读入微电网的基础参数和运行数据，同时给定原始变量与对偶变量的初值，并保证松弛变量u、l≥0，拉格朗日乘子y≠0、z≥0、w≥0，障碍因子μ≥0，设置初始迭代次数k＝0、最大迭代次数K_max、收敛标准差ε₁、ε₂；

(2)判断所需调整控制变量是否为离散变量；若是离散变量，则对其进行历史拟合为连续的最优目标变量，然后转入(3)，若为连续变量，则直接转入(3)；

(3)利用AMD算法的根据节点度的上限值来选择要编号节点原理，对改进内点法修正方程的系数矩阵进行节点优化编号；

(4)计算互补间隙Gap与K-T条件的最大范数F_max＝max{|||L_x||，||L_y||，||L_z||，||L_w||}；

(5)判断Gap＜ε₁且F_max＜ε₂是否成立，不成立直接转入(6)，若成立则输出最优解结束计算；

(6)计算各类函数的雅各比矩阵与海森矩阵

(7)求解仿射方程原变量及对偶变量的仿射步长及放射方向下的互补间隙Gap^Aff；

(8)根据预测中心参数σ＝(Gap^Aff/Gap)³，计算障碍因子μ(μ＝σ×Gap/2m，m为不等式方程的个数)；

(9)求解迭代方程，得到迭代方向Δx、Δy、Δu、Δw、Δl、Δz；

(10)求解原始变量与对偶变量的迭代步长step_d、step_d，更新原始变量与对偶变量；

(11)判断当前迭代次数k是否小于最大迭代次数k_max，若满足则置k＝k+1并转入(4)，不满足则“输出计算不收敛”并终止计算。

上述虽然结合附图对本发明的具体实施方式进行了描述，但并非对本发明保护范围的限制，所属领域技术人员应该明白，在本发明的技术方案的基础上，本领域技术人员不需要付出创造性劳动即可做出的各种修改或变形仍在本发明的保护范围以内。