一种基于混合粒子群优化算法的PSS4B参数整定方法与流程
本发明涉及一种电力系统稳定器PSS4B的参数优化整定方法,属于电网安全稳定控制领域,主要用于抑制电力系统低频振荡。
背景技术:
2000年,加拿大魁北克水电系统中,存在长距离、大负荷的输电线路,并与邻近电网通过直流线路异步互联。为了折衷孤岛模式下机组运行限制和系统频率要求之间的冲突,特定的调速器运行模式引发了缓慢的机械功率摆动,魁北克水电系统中产生了约0.05Hz的全局振荡模式。为了处理这一超低频振荡模式,魁北克水电局提出了一种多频段电力系统稳定器(PSS)的设计结构。与传统PSS单频段分支结构不同,多频段PSS将工作区间分为低、中、高三个独立可调的频段,并且分别配置一个差分滤波器及相应的超前-滞后补偿环节,可实现在更宽频率范围内提供优良的阻尼,对低于0.1Hz的超低频率振荡具有较好的抑制效果。这种多频段PSS被收录入IEEE 421.5-2005标准,即PSS4B型电力系统稳定器。
在工业应用方面,ABB公司首先根据IEEE 421.5-2005标准将PSS4B商品化。随后,国电南瑞科技股份有限公司、南瑞继保电气有限公司和广州擎天实业有限公司分别在其励磁调节器中实现了PSS4B功能。随着我国区域电网互联的发展,区域间振荡频率可能低于0.1Hz,PSS4B型电力系统稳定器由于其在超低频段抑制振荡的巨大潜力而受到广泛关注。近年来,PSS4B的研究主要集中在参数整定及优化、时域仿真和现场试验等方面。根据当前研究现状,搜索到相关的专利及文献主要有:
(1)袁亚洲,许其品,等.基于RTDS的多频段电力系统稳定器效果验证[J].电力系统自动化,2013,18(37);126-131.
(2)杜颖,王克文,等.PSS4B型电力系统稳定器参数整定[J].电测与仪表,2014,21(51);67-73.
(3)朱良合,李文意,等.新型电力系统稳定器模型分析及参数协调优化[J].水电能源科学,2014,6(32):171-175.
(4)谢欢,赵晓伟,等.一种电力系统稳定器的参数整定方法及装置[P].华北电力科学研究院有限责任公司:CN 105356486 A,2016.
文献(1)在RTDS数模仿真平台上建立单机无穷大模型,经RTDS输入输出板卡与南瑞电控NES5100励磁调节器构成控制闭环,通过修改发电机转动惯量来模拟不同本机振荡频率下的扰动试验,对比系统在0.3Hz、0.8Hz和2Hz三个典型频率下无PSS和投入PSS4B的阻尼效果。
文献(2)首先通过小干扰稳定分析确定系统机电振荡模式及PSS4B安装位置,其次在中心频率法基础上对PSS4B各频段的中心频率和增益进行调整,最后在一个8机24节点系统中模拟系统的多运行方式,证明装设PSS4B后受关注的振荡模式阻尼比均得到了有效提高。
文献(3)基于中心频率法,将PSS4B待优化参数划分为两类,采用粒子群优化算法提出一种通过两次相位补偿实现参数逐级优化整定的方法,计算量大,过程较为复杂。
专利(4)基于IEEE 421.5-2005标准提供的PSS4B典型参数,提出一种仅对高频段相位补偿环节进行整定的新方法,较为依赖调试人员的经验,效率不高。另外,对于无补偿相频特性滞后较大的三机励磁系统,仅整定高频段的两阶超前-滞后相位补偿环节时间常数,不能在全频段满足行业标准的相位补偿要求。
综上所述,对于现场PSS参数整定,需要开发一种简便易行、适用范围广的PSS4B电力系统稳定器参数优化整定方法。
技术实现要素:
本发明所要解决的问题是,克服目前PSS4B参数优化整定方法的不足,提供一种基于混合粒子群优化算法的PSS4B参数整定方法,简便易行,且同时适用于常规自并励励磁系统和无补偿相频特性滞后较大的三机励磁系统。
为实现上述目的,本发明采取以下技术方案:
一种基于混合粒子群优化算法的PSS4B参数整定方法,包括以下步骤:
步骤1:现场测量励磁系统无补偿相频特性
步骤2:将电功率信号乘以一阶惯性环节转化为转速信号,从而将以电功率Pe和转子转速偏差Δω为输入信号的电力系统稳定器PSS4B双输入模型转化为以转速偏差Δω为输入信号的单输入模型;由单输入模型得到PSS4B的传递函数TF;
其中,s=jΔw=j2πf;KL、KL1、KL2、KL11、KL17、TL1、TL2、TL7、TL8、KI、KI1、KI2、KI11、KI17、TI1、TI2、TI7、TI8、KH、KH1、KH2、KH11、KH17、TH1、TH2、TH7、TH8为PSS4B带通环节的增益和时间常数,可根据IEEE 421.5-2005标准给出的PSS4B典型参数进行设置;TL3、TL4、TL5、TL6和TL9、TL10、TL11、TL12分别为PSS4B低频段正负两个分支的的超前-滞后相位补偿环节时间常数;TI3、TI4、TI5、TI6和TI9、TI10、TI11、TI12分别为PSS4B中频段正负两个分支的的超前-滞后相位补偿环节时间常数;TH3、TH4、TH5、TH6和TH9、TH10、TH11、TH12分别为PSS4B高频段正负两个分支的的超前-滞后相位补偿环节时间常数;各频段中,正、负两个分支的超前-滞后相位补偿环节时间常数相等,以高频段为例,即TH3=TH9,TH4=TH10,TH5=TH11,TH6=TH12;
再计算传递函数TF的相角Phase(TF),即为PSS4B的相频特性中待定参数为PSS4B超前-滞后相位补偿环节时间常数;
步骤3:根据励磁系统的不同,设置不同的待优化变量;
对于常规自并励励磁系统,令PSS4B低频段和中频段超前-滞后相位补偿环节的时间常数为0;设置PSS4B的相频特性中待优化变量为PSS4B高频段超前-滞后相位补偿环节时间常数:
TH3,TH4,TH5,TH6∈[0.01,10];
对于无补偿相频特性滞后较大的三机励磁系统,设置PSS4B的相频特性中待优化变量为PSS4B低中高三个频段的超前-滞后相位补偿环节时间常数:
步骤4:根据步骤3中设置的待优化变量,以励磁系统无补偿相频特性和PSS4B的相频特性相加为0为目标,建立PSS4B参数优化模型;
步骤5:基于混合粒子群优化算法求解PSS4B参数优化模型,得到待优化变量的取值。
所述步骤1具体为:在发电机并网运行,有功功率大于额定有功功率的80%,无功功率小于额定无功功率的20%这一工况下,将电力系统稳定器PSS4B退出并用动态信号分析仪产生一个伪随机信号替代电力系统稳定器PSS4B输出信号,接入励磁调节器PSS信号输出点,用频谱仪测量输出的伪随机信号与发电机机端电压信号之间的相频特性,即为励磁系统无补偿相频特性
所述步骤4中,PSS4B参数优化模型为:
其中,为励磁系统的无补偿相频特性上频率点fm对应的相位大小;
为PSS4B的相频特性上频率点fm对应的相位大小;
为励磁系统有补偿相频特性;
fm(m=1,2,…,M)为0.1~2.0Hz范围内的M个频率点;fb为本机振荡点频率。
所述步骤5具体包括以下步骤:
①设在D维的空间中,有一个种群,其中包含了N个粒子,第i个粒子进行第t次迭代的位置记为Xi(t)=[xi,1(t),…,xi,j(t),…,xi,D(t)],i=1,2,…,N;速度记为Vi(t)=[vi,1(t),…,vi,j(t),…,vi,D(t)],i=1,2,…,N;设定的粒子各维度位置和速度的最大、最小值,分别为记为Xmax、Xmin、Vmax和Vmin【Xmax、Xmin可根据待优化变量的取值范围[0.01,10]分别设定为0.01和10;Vmax不大于Xmax,Vmin不小于Xmin】;t为迭代次数,初始化t=1;设置最大迭代次数;使用rand函数随机产生种群中各粒子的初始位置Xi(1)和速度Vi(1);每个粒子的位置代表一组待优化变量的取值;空间维数D等于待优化变量的个数,对于常规自并励励磁系统,设置D=4,Xi(t)中的4个维度位置分别代表TH3,TH4,TH5,TH6的取值;对于无补偿相频特性滞后较大的三机励磁系统,D=12,Xi(t)中的12个维度位置分别代表TL3,TL4,TH5,TL6,TI3,TI4,TI5,TI6,TH3,TH4,TH5,TH6的取值;
②对于每一个粒子,按以下步骤计算考虑了约束条件的粒子的适应值F;
1)将粒子的位置作为一组待优化变量的取值,代入步骤2得到的PSS4B的相频特性中,计算PSS4B的相频特性上频率点fm对应的相位大小
2)读取步骤1测得的励磁系统无补偿相频特性上频率点fm对应的相位大小
3)根据公式计算励磁系统有补偿相频特性上频率点fm对应的相位大小
4)判断是否满足以下约束条件:
当满足约束条件时,令粒子的适应值F=J;
当不满足约束条件任何一项时,首先通过以下方法计算惩罚项(使用惩罚策略来考虑约束条件):当励磁系统有补偿相频特性或时,pun=10000;当在本机振荡点频率fb处,若或pun=1000;然后在J上加上一个相应的惩罚项pun,得到粒子的适应值F:F=J+pun。
③将当前各粒子的位置和粒子的适应值存储在各粒子的个体最优解pbest(t)中,比较所有粒子的个体最优解pbest(t)中的适应值,得到适应值最小的粒子,将其位置和适应值存储于种群最优解gbest(t)中;
④进入迭代过程,根据以下公式来更新粒子的速度和位置:
vi,j(t+1)=wvi,j(t)+c1r1[pbest(t)-xi,j(t)]+c2r2[gbest(t)-xi,j(t)]
xi,j(t+1)=xi,j(t)+vi,j(t+1)
Xi(t+1)=[xi,1(t+1),…,xi,j(t+1),…,xi,D(t+1)],i=1,2,…,N
Vi(t+1)=[vi,1(t+1),…,vi,j(t+1),…,vi,D(t+1)],i=1,2,…,N
其中,Xi(t+1)表示第t次迭代得到的第i个粒子的位置;Vi(t+1)表示第t次迭代得到的第i个粒子的速度;若xi,j(t+1)超出最大值Xmax或最小值Xmin,则用Xmax或Xmin替代;若vi,j(t+1)超出最大值Vmax或最小值Vmin,则用Vmax或Vmin替代;w为惯性权重,c1和c2为正的学习因子【w通常取0.7-0.9,c1和c2通常取2】,r1和r2为0到1之间均匀分布的随机数;
⑤根据步骤②中粒子的适应值F的计算方法更新每个粒子的适应值F;并根据粒子的适应值F更新个体最优解pbest(t)和种群最优解gbest(t):
分别将每个粒子的适应值F与存储在其个体最优解pbest(t)中的适应值相比,如果适应值F小于存储在其个体最优解pbest(t)中的适应值,则将pbest(t)中存储的粒子位置和适应值更新为粒子当前的位置和适应值;并将所有粒子当前的个体最优解pbest(t)中的适应值与存储在种群最优解gbest(t)中的适应值相比,得到当前适应值最小的粒子,将gbest(t)中存储的粒子位置和适应值更新为当前适应值最小的粒子的位置和适应值;
⑥根据杂交概率选取指定数量【根据经验设置】的粒子放入杂交池内,池中的粒子随机两两杂交产生同样数目的子代粒子,子代粒子的位置和速度计算公式如下:
其中,p为0到1之间的随机数;parent1(x)和parent2(x)分别为两个双亲粒子的位置;parent1(v)和parent2(v)分别为两个双亲粒子的速度;child1(x)和child2(x)分别为两个子代粒子的位置;child1(v)和child2(v)分别为两个子代粒子的速度;
⑦使用步骤⑥中公式生成的子代粒子取代其双亲粒子;
⑧判断当前迭代次数是否等于最大迭代次数,若等于,则停止搜索,将存储在种群最优解gbest(t)中的粒子位置和适应值输出,输出的粒子位置即为待优化变量的取值;否则,令迭代次数加1,并返回④继续搜索。
所述PSS4B参数优化模型中,M=20,在0.1~2.0Hz范围每隔0.1Hz取一个点,得到20个频率点。
所述最大迭代次数通常在50-60范围内取值;粒子数目N=20。
有益效果:
本发明在PSS4B电力系统稳定器一种常用的参数设置方法——中心频率法基础上,根据励磁系统无补偿相频特性的不同,灵活地选择PSS4B的超前-滞后相位补偿环节时间常数进行参数优化整定,同时兼备了灵活性和适用性。对于常规自并励励磁系统,仅优化高频段的超前-滞后相位补偿环节时间常数;对于无补偿相频特性滞后较大的三机励磁系统,以低、中、高三个频段的超前-滞后相位补偿环节时间常数作为待优化变量。利用混合粒子群优化算法进行PSS4B参数整定,借鉴遗传算法中的杂交概念,在每次迭代中根据杂交概率选取指定数量的粒子放入杂交池中,两两杂交产生同样数目的子代粒子,并用子代粒子替换亲代粒子。这种方法使粒子具有跳跃更新的能力,同时使粒子的多样性得到增长,可以较好地克服局部最优问题,提高了PSS4B参数寻优的效果。本发明能高效便捷地满足不同类型励磁系统的相位补偿要求。使用本发明的方法,能够较好地发挥PSS4B在多频段抑制系统低频振荡的能力。
附图说明
图1是PSS4B数学结构图,图1(a)为PSS4B整体模型,图1(b)为PSS4B中电功率和转速分支的两个速度传感器。
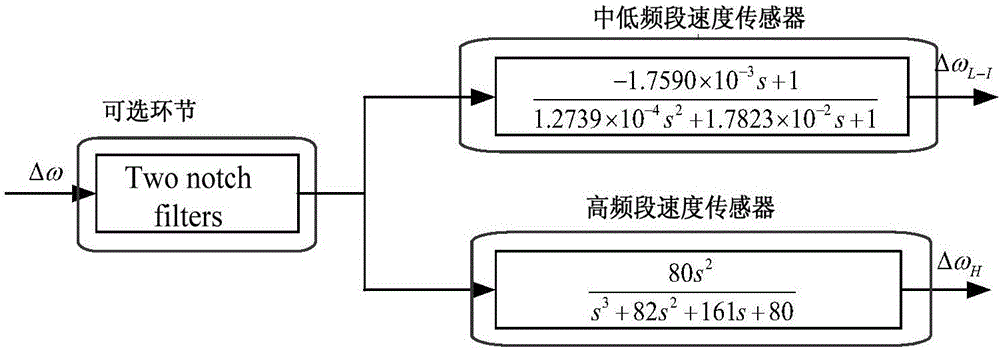
图2是PSS4B单输入模式下的低中频段、高频段速度传感器示意图。
图3是PSS4B高频段简化传递函数。
图4是PSS4B高频段带通滤波器结构。
图5是IEEE 421.5-2005标准中PSS4B的典型参数下,高频段带通滤波器频率特性;图5(a)为幅值特性,图5(b)为相位特性。
图6是基于中心频率法的单输入模式PSS4B数学结构图,此时不考虑三个频段的超前-滞后相位补偿环节。
图7是IEEE 421.5-2005标准中PSS4B典型参数时,单输入模式下考虑速度传感器环节的低、中、高各频段频率特性及全频段频率特性图;图7(a)为幅值特性,图7(b)为相位特性。
图8是基于中心频率法的单输入模式PSS4B数学结构图,此时仅优化高频段的两阶超前-滞后相位补偿环节时间常数,适用于常规自并励励磁系统;图8(a)为适用于常规自并励励磁系统PSS4B整体模型,图8(b)为经变换后PSS4B单输入模式下的低中频段、高频段速度传感器示意图。
图9是基于中心频率法的单输入模式PSS4B数学结构图,此时优化低、中、高三个频段的两阶超前-滞后相位补偿环节时间常数,适用于无补偿相频特性滞后较大的三机励磁系统;图9(a)为适用于常规自并励励磁系统PSS4B整体模型,图9(b)为经变换后PSS4B单输入模式下的低中频段、高频段速度传感器示意图。
图10为混合粒子群优化算法流程图。
具体实施方式
下面结合附图和实施例对本发明进行详细的描述,具体包括以下步骤:
第一步,励磁系统无补偿相频特性测量。在发电机并网运行,有功功率接近于额定值(80%以上),无功功率尽可能小(小于20%)这一工况下,用频谱仪测量励磁系统无补偿相频特性,在0.1~2.0Hz范围内取20个频率点,读取在选定频率点的相角。
第二步,将PSS4B双输入模式转化为单输入模式。IEEE 421.5-2005标准中的PSS4B数学模型如图1,可见PSS4B以电功率Pe和转子转速偏差Δω为输入信号,分别通过两个速度传感器得到中低频段输入信号ΔωL-I和高频段输入信号ΔωH。根据电功率信号乘以一阶惯性环节变为转速信号这一原则,可将电功率输入转化为转速输入,如图2所示。
第三步,根据励磁系统无补偿相频特性选择PSS4B待优化变量,具体包括以下步骤:
1)PSS4B性能分析。PSS4B是在PSS2B基础上改进而提出的新型电力系统稳定器,其主要特点是将输入信号处理后分为低频段(L)、中频段(I)、高频段(H)三个独立的输入通道,即多频段结构,如图1所示。其中低频段范围为0.04~0.1Hz,主要针对电力系统中的全局振荡模式;中频段为0.1~1Hz,主要针对电力系统中的区域振荡模式;高频段范围是1~4Hz,主要针对厂站内机组间振荡模式和本机振荡模式。PSS4B的三个频段具有相同的结构,每个频段可独立地设置滤波器参数、超前-滞后相位补偿、增益和限幅值,具有极高的灵活性,从而为不同频段的振荡模式提供合适的阻尼。
PSS4B的每个频段分为正、负两个分支,每个分支由分支增益Ki1(2)(i=L、I、H)、一个混合模块及两阶超前-滞后相位补偿环节构成。以高频段为例,如果将正、负两个分支的超前-滞后相位补偿环节设置为相同的参数,即TH3=TH9,TH4=TH10,TH5=TH11,TH6=TH12,则高频段传递函数可简化为图3所示。
PSS4B的参数主要集中在图3所示的滤波器环节,将该差分滤波器设置为对称的带通滤波器形式即可大大简化PSS4B的参数设置,带通形式的滤波器如图4所示。此时KH1=KH2,KH11=KH17=1,TH2=TH7=T,TH1=T/R,TH8=T*R,R为决定带通宽度的常数。图4所示带通滤波器的传递函数可表示为:
该传递函数的中心频率为:
即ω=ωH时带通滤波器的幅值最大,相位为0,幅值为:
为了使带通滤波器环节在其中心频率ωH处的幅值为1,则:
TH1=TH2/R
TH8=TH7×R
这种将各频段正、负两个分支的超前-滞后补偿环节设置为相同参数,且使其滤波器环节在中心频率Fi(i=L、I、H)处幅值为1,相位为0的参数设置方法称为中心频率法。根据中心频率法,PSS4B的参数设置主要体现在低、中、高三个频段的中心频率FL、FI、FH和相应的频段增益KL、KI、KH。以IEEE 421.5-2005标准中的典型参数为例,FH=8.0Hz,R=1.2,则高频段滤波器环节的传递函数如图5所示。由图5结合图3可知,在高频段中心频率FH=8.0Hz处,高频段滤波器环节幅值为1,相位为0;当不设置两阶超前-滞后相位补偿环节时,整个高频段在中心频率处的增益为KH。由图5相位特性可知,在中心频率FH之前为超前相位,在中心频率之后为滞后相位。
图6是基于中心频率法的单输入模式PSS4B数学结构图,此时不考虑三个频段的超前-滞后相位补偿环节。根据中心频率法,IEEE 421.5-2005标准给出了一组PSS4B典型参数,如表1。
表1 为IEEE 421.5-2005标准给出的PSS4B典型参数。
注:Ti3=Ti4=Ti5=Ti6=Ti9=Ti10=Ti11=Ti12=0(i=L、I、H)。
由表1PSS4B典型参数,图6单输入模式下考虑速度传感器环节的低、中、高各频段频率特性及全频段频率特性如图7。由三个频段的频率特性可知,其中心频率分别为0.07Hz、0.7Hz和8.0Hz,在相应的中心频率处幅值最大且相位为0。
2)PSS4B待优化变量选取。由图7全频段频率特性可知:在0.1Hz以下,低频段在全频段中起主导作用;在0.1~1Hz之间,中频段居主导地位;当大于1Hz时,低频段和中频段的作用相对微弱,全频段特性基本由高频段主导。表1典型参数下PSS4B在0.1~2Hz范围内提供的相位超前角在40~50°左右,且整体趋势较为平滑。然而,根据实际工程经验,常规自并励励磁系统在频率大于1Hz时,相位滞后均超过90°;对于无补偿相频特性滞后较大的三机励磁系统,当频率大于1Hz时,相位滞后甚至达到150~160°
之多。因此,根据PSS4B典型参数的相频特性特点,对于常规自并励励磁系统,优化整定高频段的两阶超前-滞后补偿环节时间常数,即可满足0.1~2Hz范围内自并励励磁系统的相位补偿要求;待优化变量为TH3、TH4、TH5、TH6,如图8所示。而对于无补偿相频特性滞后较大的三机励磁系统,在0.1~2Hz范围内相位滞后角的差值可能达到130°,高频段的两阶超前-滞后补偿环节不能实现0.1~2Hz整个频段的相位补偿,此时借助PSS4B三个频段并联的优势,同时优化整定低、中、高三个频段的两阶超前-滞后相位补偿环节时间常数,以满足三机励磁系统的相位补偿要求;待优化变量为TL3、TL4、TL5、TL6、TI3、TI4、TI5、TI6、TH3、TH4、TH5、TH6,如图9所示。
第四步,以PSS4B产生的附加力矩与Δω轴同相为目标,基于混合粒子群算法优化整定PSS4B超前-滞后相位补偿环节时间常数,其步骤如下:
1)假设励磁系统的无补偿相频特性为PSS4B的相频特性为则励磁系统有补偿相频特性可得出优化模型为:
其中,J为优化模型的目标函数;minJ表示求目标函数J的最小值;
根据行业标准DL/T1231-2013《电力系统稳定器整定试验导则》规定,PSS附加力矩的相位在0.3~2.0Hz范围内应落在Δω轴的-45°~20°之间;当低于0.2Hz时,最大超前角不应大于40°;在本机振荡频率处应落在Δω轴-30°~0°之间。
对于常规自并励励磁系统,PSS4B相频特性计算模型如图8,约束条件和待优化变量设置为:
对于无补偿相频特性滞后较大的三机励磁系统,PSS4B相频特性计算模型如图9,约束条件设置为:
其中fm为0.1~2.0Hz范围内的频率点,通常每隔0.1Hz取一个点,M=20;fb为本机振荡点频率。
2)混合粒子群优化算法流程如图10,具体实施步骤如下:
①设在D维的空间中,有一个种群,其中包含了N个粒子,第i个粒子进行第t次迭代的位置记为Xi(t)=[xi,1(t),…,xi,j(t),…,xi,D(t)],i=1,2,…,N;速度记为Vi(t)=[vi,1(t),…,vi,j(t),…,vi,D(t)],i=1,2,…,N;设定的粒子各维度位置和速度的最大、最小值,分别为记为Xmax、Xmin、Vmax和Vmin;t为迭代次数,初始化t=1;设置最大迭代次数;使用rand函数随机产生种群中各粒子的初始位置Xi(1)和速度Vi(1);每个粒子的位置代表一组优化变量的取值;空间维数D等于待优化变量的个数;
②对于每一个粒子,按以下步骤计算考虑了约束条件的粒子的适应值F;
1)将粒子的位置作为一组PSS4B相位补偿环节时间常数,代入步骤2得到的PSS4B的相频特性中,计算PSS4B的相频特性上频率点fm对应的相位大小
2)读取步骤1测得的励磁系统无补偿相频特性上频率点fm对应的相位大小
3)根据公式计算励磁系统有补偿相频特性上频率点fm对应的相位大小
4)判断是否满足以下约束条件:
当满足约束条件时,令粒子的适应值F=J;
当不满足约束条件任何一项时,首先通过以下方法计算惩罚项(使用惩罚策略来考虑约束条件):当励磁系统有补偿相频特性或时,pun=10000;当在本机振荡点频率fb处,若或pun=1000;然后在J上加上一个相应的惩罚项pun,得到粒子的适应值F:F=J+pun。
③将当前各粒子的位置和粒子的适应值存储在各粒子的个体最优解pbest(t)中,比较所有粒子的个体最优解pbest(t)中的适应值,得到适应值最小的粒子,将其位置和适应值存储于种群最优解gbest(t)中;
④进入迭代过程,根据以下公式来更新粒子的速度和位置:
vi,j(t+1)=wvi,j(t)+c1r1[pbest(t)-xi,j(t)]+c2r2[gbest(t)-xi,j(t)]
xi,j(t+1)=xi,j(t)+vi,j(t+1)
Xi(t+1)=[xi,1(t+1),…,xi,j(t+1),…,xi,D(t+1)],i=1,2,…,N
Vi(t+1)=[vi,1(t+1),…,vi,j(t+1),…,vi,D(t+1)],i=1,2,…,N
其中,Xi(t+1)表示第t次迭代得到的第i个粒子的位置;Vi(t+1)表示第t次迭代得到的第i个粒子的速度;若xi,j(t+1)超出最大值Xmax或最小值Xmin,则用Xmax或Xmin替代;若vi,j(t+1)超出最大值Vmax或最小值Vmin,则用Vmax或Vmin替代;w为惯性权重,c1和c2为正的学习因子,r1和r2为0到1之间均匀分布的随机数;
⑤根据步骤②中粒子的适应值F的计算方法更新每个粒子的适应值F;并根据粒子的适应值F更新个体最优解pbest(t)和种群最优解gbest(t):
分别将每个粒子的适应值F与存储在其个体最优解pbest(t)中的适应值相比,如果适应值F小于存储在其个体最优解pbest(t)中的适应值,则将pbest(t)中存储的粒子位置和适应值更新为当前的粒子位置和适应值;并将当前所有粒子的个体最优解pbest(t)中的适应值与存储在种群最优解gbest(t)中的适应值相比,得到当前适应值最小的粒子,将gbest(t)中存储的粒子位置和适应值更新为当前适应值最小的粒子的位置和适应值;
⑥根据杂交概率选取指定数量【根据经验设置】的粒子放入杂交池内,池中的粒子随机两两杂交产生同样数目的子代粒子,子代粒子的位置和速度计算公式如下:
其中,p为0到1之间的随机数;parent1(x)和parent2(x)分别为两个双亲粒子的位置;parent1(v)和parent2(v)分别为两个双亲粒子的速度;child1(x)和child2(x)分别为两个子代粒子的位置;child1(v)和child2(v)分别为两个子代粒子的速度;
⑦使用⑥中公式生成的子代粒子取代其双亲粒子;
⑧判断当前迭代次数是否等于最大迭代次数,若等于,则停止搜索,将存储在种群最优解gbest(t)中的粒子位置和适应值输出,输出的粒子位置即为待优化变量的取值;否则,令迭代次数加1,并返回④继续搜索。
根据得出的待优化变量的取值,并根据单输入模式求解PSS4B的相频特性与无补偿相频特性相加可得励磁系统有补偿相频特性
由于PSS4B三分支并联的结构,在相位补偿环节完成之后,需要同比例地缩放低、中、高三个频段增益KL、KI、KH来确定临界增益。令KL=K*K’L、KI=K*K’I、KH=K*K’H,其中K为PSS4B三分支叠加后的输出总增益,如图8和图9所示。缓慢增大K直到临界增益,并将临界增益的1/3~1/5作为最大增益整定值。
下面通过实例说明本发明的应用效果。
实施例一
对于常规自并励励磁系统,一组实测无补偿相频特性如表2。当频率在1.4Hz以上时,相位滞后均大于90°;在本机振荡频率1.6Hz处,励磁系统相位滞后112.28°。
表2 自并励励磁系统无补偿相频特性
例一中,PSS4B低、中、高三个频段的中心频率FL、FI、FH和相应的频段增益KL、KI、KH采用IEEE 421.5-2005标准中给出的典型参数,如表1。运用混合粒子群算法进行PSS4B参数优化,优化变量为TH3、TH4、TH5、TH6。经迭代后输出一组优化参数:TH3=0.062,TH4=0.010,TH5=1.240,TH6=0.625。对应的PSS4B有补偿相频特性如表3,可知PSS4B优化参数的相位补偿效果在0.1~2.0Hz频率范围内满足行业标准要求。整定高频段相位补偿环节时间常数后,即可根据临界增益法整定最大增益K。
表3 自并励励磁系统PSS4B有补偿相频特性
实施例二
表4为一组实测三机励磁系统无补偿相频特性,当频率在0.7Hz以上时,相位滞后均大于90°;在本机振荡频率1.9Hz处相位滞后多达150.09°。在0.1~2Hz范围内,相位滞后角的差值达到136.13°,可见其整体滞后特性较大。
表4 三机励磁系统无补偿相频特性
例二中,PSS4B低、中、高三个频段的中心频率FL、FI、FH和相应的频段增益KL、KI、KH采用IEEE 421.5-2005标准中给出的典型参数,如表1。运用混合粒子群算法进行PSS4B参数优化,优化变量为TL3、TL4、TL5、TL6、TI3、TI4、TI5、TI6、TH3、TH4、TH5、TH6。经迭代后输出一组优化参数:TL3=0.644,TL4=0.753,TL5=0.516,TL6=1.661,TI3=0.010,TI4=1.240,TI5=0.496,TI6=0.010,TH3=0.171,TH4=0.010,TH5=0.684,TH6=0.933。对应的PSS4B有补偿相频特性如表5,可知PSS4B优化参数的相位补偿效果在0.1~2.0Hz频率范围内满足行业标准要求。整定低、中、高三个频段相位补偿环节时间常数后,即可根据临界增益法整定最大增益K。
表5 三机励磁系统PSS4B有补偿相频特性
- 还没有人留言评论。精彩留言会获得点赞!