一种分析低频调制信号在HXD型机车整流器传播规律的方法与流程

本发明属于高速铁路牵引供电电能质量分析领域，具体涉及一种分析低频调制信号在HXD型机车整流器传播规律的方法。

背景技术：

HXD、EMUs是典型的非线性负荷，在采用“交-直-交”方式后较好地克服了功率因数较低的缺点。然而大量电力机车升弓取流整备时，使得牵引网网压较大波动，导致机车继保装置动作，IGBT出现自锁，甚至引发运输瘫痪。现场通过电力列车渐进式升弓方式来抑制该问题，但无法从根本上解决问题。

针对该现象，研究均从低频振荡角度研究牵引网电气量不稳定问题。电力系统中低频振荡问题主要表征为扰动下发电机转子间的相互摇摆，在缺乏阻尼时引起的持续振荡。目前，针对低频振荡产生机理主要有：负阻尼机理、强迫振荡机理和混沌理论。此外，现有技术还研究了电网链式分布、区域间功率不平衡等对电力系统低频振荡进行阻尼影响分析。考虑牵引供电系统拓扑结构的特殊性、负载的随机性及非线性，与理论分析的对象、产生过程及数学建模均存在差异，因而不可以简单地归结为低频振荡问题，需深入挖掘牵引网实际监测数据的隐含信息。

技术实现要素：

本发明所要解决的技术问题是提供一种分析低频调制信号在HXD型机车整流器传播规律的方法，准确定位牵引网电压波动的特征；对维护高速铁路牵引供电系统的安全稳定运行具有非常重要的实际工程意义。

为解决上述技术问题，本发明采用的技术方案是：

一种分析低频调制信号在HXD型机车整流器传播规律的方法，包括以下步骤：

步骤1：利用DFT变换与TLS-ESPRIT结合的方法对牵引网、机车中间直流环节实际监测数据的隐含信息进行挖掘，确定网侧、中间直流侧引发波动的具体模态，网压频率信号与整流器中间直流电压频率成份的关系为：

式中，u_ab为机车整流器输入端电压；U_kr和b_kr分别表示整流器输出调制信号电压的幅值和谐波能量系数，k＝1，2，3…，U_dc为整流器输出电压中的直流电压分量；

步骤2：构建在步骤1所示模态下的牵引网网压波动信号的数学模型：

式中，m_i、m_hj为基波、谐波的调制系数，其取值范围为0～1；表示基波的初始相位角；f_hj和分别表示谐波频率和初始相位；

步骤3：再利用步骤2中所构造出的数学模型，推导其在SPWM算法下的传播机理为：

式中，S_(t)表示整流器开关函数，N表示电压量含有的总谐波次数。

与现有技术相比，本发明的有益效果是：

1.针对多车接入牵引供电系统引发的电气量不稳定问题，本发明使用DFT与TLS-ESPRIT相结合的方法确定了牵引网电气量不稳定现象并非低频振荡问题，而是电能质量电压波动问题；并对其主导模态给出准确辨识结果；

2.从数学推导的角度，明确了整流器两端的谐波传递的数学关系，为电压波动的有效抑制奠定了理论基础。

附图说明

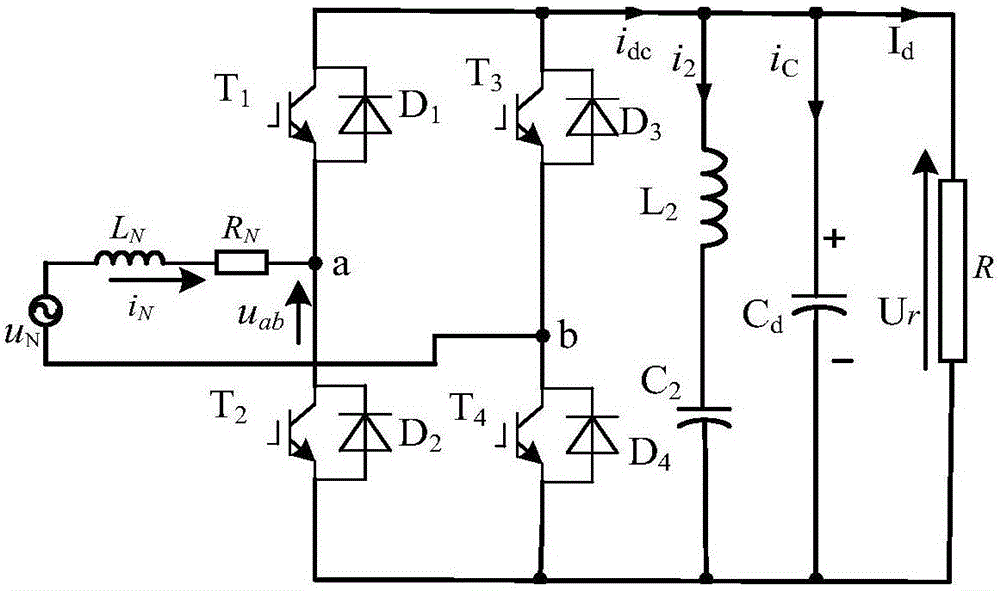
图1是HXD型电力机车单相两电平脉冲整流器主电路。

图2是网侧牵引变流器开关函数图。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细的说明。本发明方法的分析对象为多车接入牵引网引发牵引网电压波动现象，主要实现步骤为：深入挖掘牵引网、机车中间直流环节实际监测数据的隐含信息，量化二者关系，并与低频调制信号在整流器中传播规律进行对比验证，其主要步骤包括以下几个方面：

1、使用DFT变换与TLS-ESPRIT结合的方法，分析的牵引网不稳定电气量模态成份；

构造多车接入牵引供电系统时的电压信号u(n)，Hankel矩阵X

式中，α_i、ω_i、A_i、θ_i分别为第i模式的衰减系数、角频率、振荡幅值和初相位；T_s为信号的采样周期；p为信号阶数，一般为实际正弦分量个数的两倍；w(n)为白噪声；称为该信号的极点；N为u的数据个数，M＝N/2，L＝N-M+1。

对X进行奇异值分解X＝UΣV^T，并确定信号子空间阶数p，构造矩阵[V₁V₂]，求取总体最小二乘解为

求矩阵Ψ_Tls的特征值λ_i(i＝1,2,……,p)，计算模式的频率和阻尼比

随后通过构造矩阵、拟合系数计算模式的幅值和初相位，进行主导模式筛选；采用频率比对的方式，确定信号的模态成份。同理，对整流器中间直流电压进行处理。结果网压频率信号与整流器中间直流电压频率成份存在如下关系：

式中，u_ab为机车整流器输入端电压；U_kr和b_kr分别表示整流器输出调制信号电压的幅值和谐波能量系数，k＝1,2,3…，U_dc为整流器输出电压中的直流电压分量。

2、考虑该现象中高次谐波成份也出现被调制现象，构造电压波动信号表示为

式中，m_i、m_hj为基波、谐波的调制系数，其取值范围为0～1；表示基波的初始相位角；f_hj和分别表示谐波频率和初始相位。

3、结合构造的数学模型，机车整流器电路如图1所示，为便于分析，定义理想开关函数S_a和S_b并忽略牵引绕组电阻，由于上桥臂与下桥臂不允许直通，则在每相桥臂中，上桥臂的开关信号必须与下桥臂的开关信号互反。采用双极性SPWM算法，开关函数如图2所示，输入端电压u_ab的取值有U_d、0、-U_d三种电平，有效的开关组合有2²＝4种，即S_ab＝00、01、10、11四种逻辑。当调制波电压大于载波电压时，S_A为1，否则为0。b相与a相调制方式相同，但b相调制波与a相调制波相位相差180°。本发明分析的牵引变流器开关函数为：

式中，J_n(x)为贝塞尔函数；ω_m为调制信号角频率；ω_c为载波信号角频率；p为调制波与载波频率比例系数(载波比的倒数)；ε为采样系数，取值一般为0～1；M为调制系数，其取值范围为0～1。

忽略谐波间的相互影响，则式(5)可简化如下：

整理后得

式(7)为牵引供电系统侧调制电压的表达式，该表达式可以准确反映出牵引供电系统侧电压受到调制的频谱特征。显然，式(7)中第一项为基波和一系列特征谐波之和，其为整流开关函数对整流器输出电压中直流电压分量U_dc的调制结果，特征谐波的频率满足2v±1的关系。其中，v＝1，2，…，∞。式(7)中第2、3、…项为一系列电压调制波之和，其为整流开关函数对整流器输出调制波电压的调制结果。

此外，式(7)表明对于频率为f_k的直流电压波动分量，其会在基波和各特征谐波附近引起等幅成对的频率成份，即n·f_m±f_k。伴随特征谐波次数、幅值的变化，调制波幅值将随之变化，考虑牵引网电压以工频为主，因而，对工频作用的调制信号主导影响网压幅值不稳定。对比式(3)、(7)可发现，两式具有高度统一性，式(3)仅是式(7)的一个特例，验证了本方法的实用性。

下面对本发明方法进行更详细的阐述。

1)、使用DFT变换分析牵引网网压各时间段主导频率能量幅值分布，如表1所示。

表1 各时间段主导频率能量幅值分布

2)、通过TLS-ESPRIT构造矩阵、拟合系数计算模式的幅值和初相位，并进行主导模式筛选。随后采用频率比对的方式，确定信号的模态成份，如表2所示。

表2 TLS-ESPRIT算法分析的牵引网电压模态

3)、描述网压频率信号与整流器中间直流电压频率成份存在数学关系，如式(3)所示。

4)、考虑该现象中高次谐波成份也出现被调制现象，构造电压波动信号，如式(4)所示。

5)、结合调制理论分析调制信号在HXD型电力列车整流器中传播机理，该推导出的公式能够反映工频作用的调制信号主导影响网压幅值不稳定现象。

6)、再无补偿装置的情况下，分析多车接入牵引网引发的电气量波动规律，验证本发明的实用性。