一种居民用户用电智能调度优化方法与流程

本发明涉及智能家庭用电技术领域，具体涉及智能家电的用电安排优化方法。

背景技术：

随着社会的发展，居民住宅用电设备在数量和容量上也在逐年增加，居民用电在电网二次侧占的比重越来越大。通过利用智能控制设备平台，实现居民智能用电。在面对火力发电污染日益严重的情况下，合理用电变得更加迫切。

然而现阶段在居民用电方面存在诸多问题需要研究，一些学者对用电设备之间的协调优化进行了研究，如：基于用户对家电的偏爱程度，预先设定的用电设备优先级，提出了可以协调用电设备用电时间的智能家庭能源管理模型。考虑电动汽车的用电成本和用户用电舒适度，研究了优化电动汽车用电策略的问题。以减小用电费用和尖峰用电量为总目标，提出了家庭能源管理系统的基本框架和家电设备优化用电的方法。

居民用户智能用电策略优化方法是构建电网二次侧健康、合理用电的重要支柱。用户根据电价和自身的用电习惯，优化安排用电设备未来一段时间内的用电计划，但目前并未有在分时电价机制下考虑用户用电厌恶度的居民用户智能用电优化策略。

技术实现要素：

本发明的目的在于为了克服现有技术的不足，提出一种基于分时电价下居民智能用电策略优化方法。根据用户用电行为和用电设备的负荷特性，分别建立负荷模型、用电厌恶度模型和用电费用模型以及智能用电调度总体模型，求解总体模型得到用电调度的最优方法。

实现上述目的的技术方案为：

居民用户用电智能调度优化方法，包括如下步骤：

步骤一：收集近期各家电的用电数据；

步骤二：根据各用电设备的用电特性分别建立负荷模型；

步骤三：根据用户用电需求构建用户用电厌恶度模型；

步骤四：建立用户用电总费用模型；

步骤五：建立智能用电调度总体模型，求解总体模型得到智能用电调度的最优方案。

进一步，所述步骤一的实现包括：根据供电商提供的分时电价政策将一小时平均划分成n段，即每小段时间为单位h，一天总时间段D＝24·n，其中取7:00～次日7:00为一天；收集最近一个月内各个智能家电设备的用电数据，其中用电数据包括各用电设备的用电起始时间、用电结束时间、用电持续时间以及运行功率。

进一步，所述步骤一还包括：对居民工作日在不同的季度的早、中、晚三个时段的到家、离家的时间建立函数，即早晨上班离家时间t₁，中午下班到家、离家时间t₂、t₃，晚上下班到家时间t₄。建立的到家-离家的时间模型如下：

其中季度A取值{-1,0,1}，A＝-1表示处于冬季，A＝0表示处于春秋季，A＝1表示处于夏季。

进一步，所述步骤二的实现包括：建立储能型设备的负荷模型；建立非储能型设备的负荷模型；所述非储能设备负荷模型包括离散型设备负荷模型与连续型设备负荷模型。

进一步，建立储能型设备的负荷模型的过程如下：

S1.1：建立储能型设备Sto在运行时间段t内的充电量表达式：

其中Z表示储能设备的总数；P_z,t表示为设备z在时间段t的充电功率：

其P_N表示设备充电的额定功率；λ_z,t表示开关变量，当λ_z,t＝0时，设备在时间段t断开电源，当λ_z,t＝1时，设备在时间段t连接电源充电。

S1.2：建立设备z实际累计充电时间的表达式：

其中分别表示设备z所允许充电的最早开始时间和最迟结束时间。

S1.3：建立设备z的荷电状态SOC的表达式：

当Soc_z,t＝0时，储能设备z放电完全，当Soc_z,t＝1时，储能设备z完全充满；其中C_z,t,C_z,d分别表示设备z在时间段t时的剩余电量和设备z完全充电状态下的容量，且其中分别表示储能设备z保持正常工作所需的最低容量和设备z的额定容量。

S1.4：建立Sto设备在运行时间段t内的放电量：

其中P'_z,t＝P'_N·λ'_z,t表示设备z在时间段t的放电功率，P'_N表示设备z放电的额定功率；λ'_z,t表示开关变量，当λ'_z,t＝0时，设备z在时间段t断开电源，当λ'_z,t＝1时，设备z在时间段t连接电网放电，且λ'_z,t＝0，1；W'_z,t＝P'_z,t·τ表示设备z在时间段t内的放电量。

S1.5：建立设备z实际累计放电时间表达式：

其中分别表示设备z所允许放电的最早开始时间和最迟结束时间。

S1.6：运用阿伦尼乌斯方程对S1.5的表达式分析，建立在其一个工作周期内的电池容量表达式：

其中A表示Arrhenius常数系数，B表示Arrhenius修正系数，表示电池在常温20℃下的标称容量，R表示摩尔气体常量，T表示绝对温度，E_a表示活化能。

进一步，建立离散型设备负荷模型的过程如下：

S2.1：建立离散型设备x在运行时间段t内的耗电量表达式：

其中X表示参与调度的Dis设备的总数；作为开关标记量，当时表示设备x在时间段t结束运行，当时表示设备x在时间段t是在工序S_i下稳定运行；约束条件：其中分别表示Dis设备x的最小运行功率和最大运行功率。

S2.2：建立离散型设备x的运行时间表达式：

进一步，建立连续型用电设备负荷模型的过程如下：

S3.1：对连续型设备y建立模型，引入标记变量λ_y,t，当λ_y,t＝0时表示用电设备y在时间段t内结束运行，当λ_y,t＝1时表示用电设备y在时间段t内保持运行，则设备y在运行时间段t内的耗电量表达式：

其中约束条件：λ_y,t＝0，1；Y表示参与调度的Con设备的总数。

S3.2：建立连续型设备y的运行时间表达式：

进一步，步骤三的实现包括：

S4.1：建立储能型设备厌恶度模型：

其中Soc_z表示设备z在充电结束时的SOC，时间比例系数其中t”_z，t”'_z分别表示设备z在时间D内的放电总时间和该设备在电价高峰期内的放电总时间，非负权重系数取值0～1。

S4.2：建立离散型设备厌恶度模型：

S4.3：建立连续型设备厌恶度模型：

其中正权重系数ζ₁，ζ₂的取值为ζ₁+ζ₂＝1。

S4.4：上述三类厌恶度模型求得居民用户总体平均厌恶度模型：

γ＝σ₁·γ_Sto+σ₂·γ_Dis+σ₃·γ_Con

其中σ₁，σ₂，σ₃为引入的非负权重系数，用户根据需求设定各个权重系数的值，其值的大小与用户对设备用电的需求程度成正比，约束条件：σ₁+σ₂+σ₃＝1。

进一步，步骤四的实现包括：建立居民用户智能用电花费ε模型：

其中W_t＝W_Sto,t+W_Dis,t+W_Con,t表示居民家中参与本次调度的各个用电设备在时间段t的耗电量总和；表示为Sto设备在时间段t时的放电量，表示供电商提供的在时间t时的电价即分时电价；约束条件其中E₀表示居民用户家中导线所允许通过的最大功率。

进一步，步骤五的实现包括：建立优化总体目标：

min{σ₄·ε+σ₅·γ}

其中σ₄+σ₅＝1，σ₄和σ₅为非负权重系数；

采用遗传算法对所述优化总体目标进行求解，得到以缴纳电费用和厌恶度两者加权和最低为目标的优化方案的负荷分布。

本发明的有益效果：

和现有的技术相比，本发明能够让用户根据个人习惯作出适时的调整，大型储能设备使电网的削峰填谷能够达到更加理想的效果，进而使电网更加稳定、健康。

附图说明

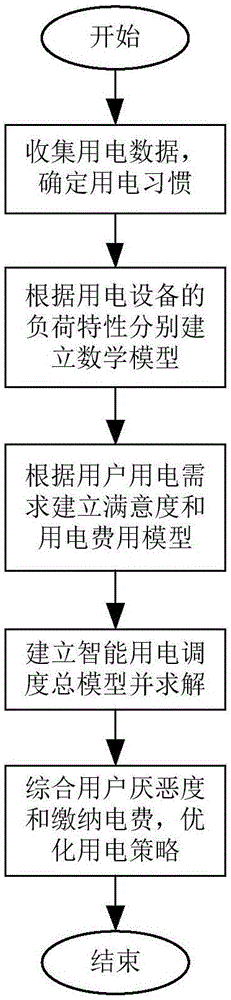
图1为本发明方法的总流程图。

具体实施方式

结合附图对本发明的具体实施方式做进一步的详细说明。

步骤一：收集近期各家电的用电数据

根据供电商提供的分时电价政策将一小时平均划分成n段，即每小段时间为单位h，一天总时间段D＝24·n，其中取7:00～次日7:00为一天。收集最近一个月内各个智能家电设备的用电数据，其中用电数据包括各用电设备的用电起始时间、用电结束时间、用电持续时间以及运行功率，进而确定居民用户用电习惯。

对居民工作日在不同的季度的早、中、晚三个时段的到家、离家的时间建立函数，即早晨上班离家时间t₁，中午下班到家、离家时间t₂、t₃，晚上下班到家时间t₄。建立的到家-离家的时间模型如下：

其中季度A取值{-1,0,1}，A＝-1表示处于冬季，A＝0表示处于春秋季，A＝1表示处于夏季。

步骤二：根据主要用电设备负荷特性建立数学模型

居民用电设备分可控设备和不可控设备两类，为了简化分析只考虑可控家电。按照各家电是否具有存储电能的特性可以将居民用电设备分为储能设备和非储能设备两类。其中非储能设备分为离散型设备与连续型设备。

(1)储能型设备

在居民日常用电设备中，储能设备z即电池类储电设备，记为Sto。对Sto设备建立模型，设备Sto在运行时间段t内的充电量：

其中Z表示储能设备z的总数；P_z,t表示为设备z在时间段t的充电功率：

其P_N表示设备z充电的额定功率；λ_z,t表示开关变量，当λ_z,t＝0时，设备z在时间段t断开电源，当λ_z,t＝1时，设备z在时间段t连接电源充电。

设备z实际累计充电时间：

其中分别表示设备z所允许充电的最早开始时间和最迟结束时间。

设备z的荷电状态SOC：

当Soc_z,t＝0时，储能设备z放电完全，当Soc_z,t＝1时，储能设备z完全充满；其中C_z,t,C_z,d分别表示设备z在时间段t时的剩余电量和设备z完全充电状态下的容量，且其中分别表示储能设备z保持正常工作所需的最低容量和设备z的额定容量。

Sto设备在运行时间段t的放电量：

其中P'_z,t＝P'_N·λ'_z,t表示设备z在时间段t的放电功率，P'_N表示设备z放电的额定功率；λ'_z,t表示开关变量，当λ'_z,t＝0时，设备z在时间段t断开电源，当λ'_z,t＝1时，设备z在时间段t连接电网放电，且λ'_z,t＝0，1；W'_z,t＝P'_z,t·τ表示设备z在时间段t内的放电量。

设备z实际累计放电时间：

其中分别表示设备z所允许放电的最早开始时间和最迟结束时间。

本发明中的电池选择锂离子电池，运用阿伦尼乌斯方程对其分析，在其一个工作周期内的电池容量：

其中A表示Arrhenius常数系数，B表示Arrhenius修正系数，表示电池在常温20℃下的标称容量，R表示摩尔气体常量，T表示绝对温度，E_a表示活化能。为了方便计算，认定温度在储能设备z的一个工作周期内保持不变。

(2)非储能设备

1)离散型用电设备

有些家居用电设备x是在以用户给予的开关信号在运行的，当该类设备接收到用户的命令，开始进入稳定运行状态，运行过程依次经历S₁,...,S_i,...,S_I道工序，其中I_x表示用电设备x的工序数目，其数值由设备本身运行特性所决定，即I＝I_x，其用电功率保持在额定功率其中表示设备x稳定运行在S_i道工序下所需的额定功率，每道工序之间无时间间隔且整个运行过程均无人为干预因素。当设备结束运行时，用电功率变为0。若设备x运行过程只有单一的功率保持，则取值I_x＝1，即例如家用电饭煲，智能电热壶等，该类设备工作过程中存在加热-保温两道工序，每个模式下的稳态功率也不一样。该类设备被定义为离散型用电设备，记为Dis。

对于Dis设备在运行时间段t内的耗电量：

其中X表示参与调度的Dis设备的总数；作为开关标记量，当时表示设备x在时间段t结束运行，当时表示设备x在时间段t是在工序S_i下稳定运行。约束条件：其中分别表示Dis设备x的最小运行功率和最大运行功率。

Dis设备x的运行时间：

2)连续型用电设备

一些家居用电设备y有一定的额定功率，稳定运行功率根据用户的需求可以选择处在最大运行功率和最小运行功率之间的任意数值的额定功率，即设备y的功率连续可调，例如可调节亮度的照明设备，其运行额定功率在一定范围内上下可调，即该类设备被定义为连续型用电设备，记为Con。

对Con设备建立模型，引入标记变量λ_y,t，当λ_y,t＝0时表示用电设备y在时间段t内结束运行，当λ_y,t＝1时表示用电设备y在时间段t内保持运行，则设备y在运行时间段t内的耗电量：

其中约束条件：λ_y,t＝0，1；Y表示参与调度的Con设备的总数。

Con设备y的运行时间：

步骤三：构建居民用户对用电设备的厌恶度模型

根据用户偏爱于设备的即时运行状态或结束状态，将用电设备分为即时需要设备和完时需要设备两类，分别记为Im和Ov，其中Ov设备分为离家前需完成任务的设备和到家前需完成的设备两类，分别记为Ov1Ov2。对于Im设备，用户对其厌恶的是在用户在家时间段内，其运行时间不在用户舒适的时间段内；对于Ov设备，用户厌恶其在用户离家，到家时尚未完成任务，对设备w＝{x,y}建立的厌恶度模型表示为：

γ_w＝ξ_w·g(t_w,end)+(1-ξ_w)·h(t_w,start,t_w,end) (13)

其中0-1型参数ξ_w＝1时，表示设备w为用户偏好于完时需要型设备Ov，ξ_w＝0时，表示设备w为用户偏好于即时需要型设备Im。g(t_w,end)，h(t_w,start,t_w,end)分别表示为Ov型和Im型设备的厌恶度函数，其Ov设备的厌恶度模型具体如下：

g(t_w,end)＝δ_w·g₁(t_w,end)+(1-δ_w)·g₂(t_w,end) (14)

其中0-1型参数δ_w表示设备w是否为用户所偏好于离家前需完成任务的Ov1设备，当δ_w＝1时，表示设备w是Ov1型；当δ_w＝0时，表示设备x是Ov2型。具体模型如下：

其中a取值2或4，b取值1或3；分别表示用户设定设备w的最早，最晚结束时间；Δt_w,tq,Δt_w,yc分别表示用户对于设备w所能忍受的最大提前完成的时间，最大延迟完成的时间。

此外，Im设备的厌恶度模型表示为：

其中Δt_w表示设备w的实际运行时间；表示用户偏爱设备w运行的起始时间和结束时间；比重系数表示设备w在用户偏爱的时间段的运行时间比例，其中表示设备w在区间内的运行时间。

进一步：对步骤二中的Sto，Dis，Con三类负荷，分别从时间、功率和任务完成程度三方面考虑用户对用电负荷的厌恶程度，并建立相应的厌恶度模型。

(1)储能型设备

Sto设备充电结束时存储的电量占完全充电状态下容量的比例大小影响用户对该类负荷运行的厌恶程度。此外，储能型设备可以很好地参与电网二次侧的削峰填谷，在用电高峰期，将日常剩余电量出售给需求方。在分时电价下，用户必然厌恶储能设备在结束运行状态时过低的储电量以及所花过高的电费，此外本发明考虑储能型设备的寿命成本，一天充放电一次。该类负荷在运行的整个时段D内的厌恶度模型如下：

其中Soc_z表示设备z在充电结束时的SOC，时间比例系数其中t”_z，t”’_z分别表示设备z在时间D内的放电总时间和该设备在电价高峰期内的放电总时间，非负权重系数取值0～1。

(2)离散型设备

Dis设备作为功率离散型设备，可以参与智能家电的调度，该类设备的工作功率有其自身的负荷特性决定的，用户对其用电厌恶度由其工作的时间因素来决定，所以这类负荷运行时的厌恶度模型如下：

其中γ_x＝γ_w,w＝x表示设备x的厌恶度。

(3)连续型设备

Con设备作为功率连续型设备，该类负荷的厌恶度主要由运行时间和功率两个因素决定，时间因素用上述γ_w函数表示。运行功率方面，其工作功率在最大和最小功率之间，厌恶度在于其工作时的功率与其标准功率的偏差的比重，所以这类负荷运行时的厌恶度模型如下：

其中表示设备y的厌恶度；f_y'表示设备y的实际用电计划；f_y表示设备y原来的用电计划；表示用户对设备y所容忍的最大用电计划偏差，且γ_y表示属于Im型或Ov型的设备y的厌恶度；引入的系数表示设备y是否属于Im型或Ov型，当表示设备y属于Im型或Ov型，当表示设备y既不属于Im型也不属于Ov型；ζ₁,ζ₂表示正权重系数，其取值为ζ₁+ζ₂＝1；P_y',分别表示设备y的实际运行功率和用户设定的最佳运行功率；分别表示设备y的最小运行功率和最大运行功率。

由上述三类厌恶度模型求得居民用户总体平均厌恶度模型：

γ＝σ₁·γ_Sto+σ₂·γ_Dis+σ₃·γ_Con (20)

其中σ₁，σ₂，σ₃为引入的非负权重系数，用户根据需求设定各个权重系数的值，其值的大小与用户对设备用电的需求程度成正比，约束条件：σ₁+σ₂+σ₃＝1。

步骤四：结合步骤一收集到的各个家电的用电数据和各地区供电商提供的分时电价政策，提出居民用户智能用电花费ε模型：

其中W_t＝W_Sto,t+W_Dis,t+W_Con,t表示居民各个用电设备在时间段t的耗电量总和，其中W_Sto,t,W_Dis,t,W_Con,t分别表示上述的Sto设备、Dis设备以及Con设备在运行时间段t的用电量；表示供电商提供的在时间t时的电价即分时电价；约束条件其中E₀表示居民用户家中导线所允许通过的最大功率。

步骤五：建立智能用电调度总模型并求解

本发明提出的智能用电建模方法，根据上述的用电设备的特性以及所处的分时电价环境下建立优化总体目标：

min{σ₄·ε+σ₅·γ} (22)

其中σ₄+σ₅＝1，σ₄和σ₅为非负权重系数。

采用遗传算法对该目标进行求解，得到以缴纳电费用和厌恶度两者加权和最低为目标的优化方案的负荷分布。

上文所列出的一系列的详细说明仅仅是针对本发明的可行性实施方式的具体说明，它们并非用以限制本发明的保护范围，凡未脱离本发明技艺精神所作的等效实施方式或变更均应包含在本发明的保护范围之内。