一种基于Matlab的快速分解法潮流计算方法与流程

本发明涉及一种电力系统快速分解法潮流计算方法，特别是一种适合研究目的使用的快速分解法潮流计算方法。
背景技术：
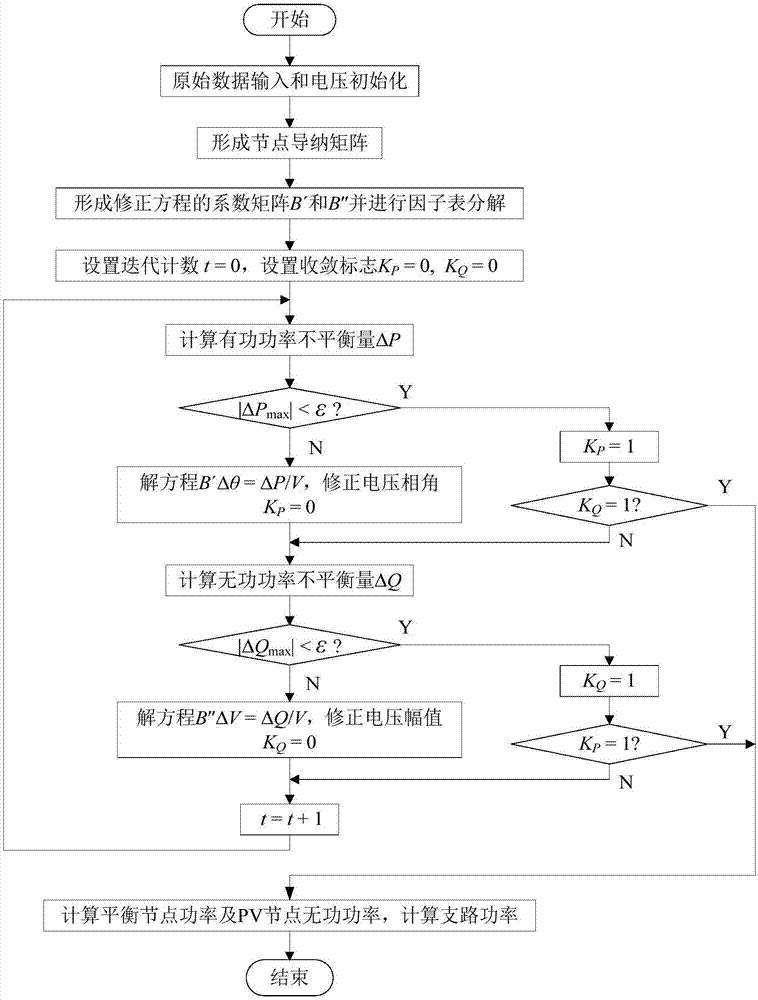
：电力系统潮流计算是研究电力系统稳态运行的一项基本计算，它根据给定的运行条件和网络结构确定整个网络的运行状态。潮流计算也是电力系统其他分析的基础，如安全分析、暂态稳定分析等都要用到潮流计算。由于具有收敛可靠、计算速度快及内存需求少的优点，快速分解法成为当前潮流计算的主流方法之一，科研人员经常以快速分解法潮流计算为基础进行进一步地研究。实用的商业软件采用稀疏矩阵技术和节点优化编号等高级技术。这些技术虽然能大幅度提高潮流计算的速度、降低内存占用量，但编程非常麻烦且难以修改和维护，不易增加新的功能，因而不适合科研人员用于研究目的使用。Matlab软件以矩阵为最基本的数据单位，可以方便地处理各种矩阵和向量运算，也可以很方便自然地处理复数类型，其指令表达式与数学中常用的形式很接近，还有大量常见且实用的函数，给编程带来很大便利。Matlab软件简单易用、代码短小易操作，易于编程和调试，计算功能强大，同时还具有非常强大的可视化图形处理和交互式功能，为科学研究以及工程应用提供了一种高效的编程工具，目前已经成为许多科学领域的基本工具和首选平台，在各种科学和工程计算领域得到了广泛的应用。为了适应越来越多的科研人员需要在Matlab平台上以快速分解法潮流计算为基础进行进一步地研究的需求，迫切需要一种基于Matlab软件的易于编程、修改和调试的快速分解法潮流计算方法。如图1所示，现有快速分解法潮流计算方法，主要包括以下步骤：A、输入原始数据和初始化电压；根据电力系统节点的特点，潮流计算把电力系统节点分成3类：节点有功功率和无功功率已知、节点电压幅值和电压相角未知的节点称为PQ节点；节点有功功率和电压幅值已知、节点无功功率和电压相角未知的节点称为PV节点；节点电压幅值和电压相角已知，节点有功功率和无功功率未知的节点称为平衡节点。电压初始化采用平启动，即PV节点和平衡节点的电压幅值取给定值，PQ节点的电压幅值取1.0；所有电压的相角都取0.0。这里相角单位为弧度，其他量单位采用标幺值。B、形成节点导纳矩阵；C、形成修正方程的系数矩阵B′和B″并进行因子表分解；潮流计算的基本方程是非线性方程组，通常采用逐次线性化方法迭代求解。线性化得到的方程称为修正方程，用来求电压幅值和相角的修正量。快速分解法修正方程是在极坐标牛顿法潮流计算修正方程基础上解耦并改进得到的。快速分解法修正方程为：B′Δθ＝ΔP/V(1)B″ΔV＝ΔQ/V(2)式中，ΔP/V和ΔQ/V分别为有功功率和无功功率不平衡量除以电压幅值后的列向量；ΔV和Δθ分别为电压幅值和电压相角修正量列向量；B′为导纳矩阵的虚部，但计算时不计及支路电阻、对地导纳和非标准变比，导纳矩阵中包含PQ节点和PV节点相关的行和列；B″为导纳矩阵的虚部，仅包括与PQ节点有关的行和列。D、设置迭代计数t＝0，设置收敛标志KP＝0，KQ＝0；E、计算有功功率不平衡量ΔP；PQ节点和PV节点的有功功率不平衡量为：式中，Pis为节点i的注入有功功率；Vi为节点i的电压幅值；θij＝θi-θj，θi、θj分别为节点i和节点j的电压相角；Gij和Bij分别为导纳矩阵元素的电导部分和电纳部分；n为节点数。求各节点中有功功率不平衡量绝对值最大的值，称为有功功率最大不平衡量，记为ΔPmax。F、判断有功功率最大不平衡量绝对值|ΔPmax|是否小于收敛精度ε；如果小于收敛精度ε，令KP＝1，转到步骤G；否则，解修正方程B'Δθ＝ΔP/V，修正电压相角，令KP＝0，转到步骤H；求解修正方程B′Δθ＝ΔP/V，得到Δθ，按下式修正电压相角：θ(t+1)＝θ(t)-Δθ(t)(4)式中，上标(t)表示第t次迭代。G、判断KQ是否等于1；如果KQ＝1，转到步骤L；H、计算无功功率不平衡量ΔQ；PQ节点的无功功率不平衡量为：式中，Qis为节点i的注入无功功率；m为PQ节点数。求各节点中无功功率不平衡量绝对值最大的值，称为无功功率最大不平衡量，记为ΔQmax。I、判断无功功率最大不平衡量绝对值|ΔQmax|是否小于收敛精度ε；如果小于收敛精度ε，令KQ＝1，转到步骤J；否则，解修正方程B"ΔV＝ΔQ/V，修正电压幅值，令KQ＝0，转到步骤K；求解修正方程B″ΔV＝ΔQ/V，得到ΔV，按下式修正电压幅值：V(t+1)＝V(t)-ΔV(t)(6)J、判断KP是否等于1；如果KP＝1，转到步骤L；K、令t＝t+1，返回步骤E进行下一次迭代；L、计算平衡节点功率及PV节点的无功功率，计算支路功率，结束。步骤E和步骤F为P～θ迭代，即通过ΔP求Δθ进而修正θ；步骤H和步骤I为Q～V迭代，即通过ΔQ求ΔV进而修正V。主流快速分解法都是按上述步骤设计方法，即先进行P～θ迭代，后进行Q～V迭代。也有文献采用先进行Q～V迭代，后进行P～θ迭代的方法。直接采用上述原理实现的快速分解法潮流计算软件计算速度较慢，商业使用的快速分解法潮流计算软件采用稀疏矩阵技术和节点优化编号技术，比较复杂，不适合科研人员以此为基础进一步进行科学研究。因此，中国专利ZL201010585176.X提出了一种适合研究目的使用的快速分解法潮流计算方法，为以快速分解法潮流计算为基础进行进一步研究的科研人员提供一个易于修改和维护的快速分解法潮流计算方法，其特点如下：(1)不采用稀疏矩阵技术和节点优化编号，大大降低了算法的实现难度；(2)通过简单逻辑判断来避免不必要运算，提高了潮流计算的计算速度。中国专利ZL201010585176.X所提出方法以快速分解法潮流计算为基础，为进一步研究的科研人员提供了一个易于修改和维护的快速分解法潮流计算方法。该方法采用C语言等编译型编程语言实现时速度很快，但使用Matlab这类解释型编程语言实现时计算速度则很慢，同时该方法也没有充分利用Matlab擅长矩阵运算和复数运算的特点。因此需要一个充分利用Matlab的特点且计算快速的快速分解法潮流计算方法供在Matlab平台上进行科学研究的科研人员使用。技术实现要素：为解决现有技术存在的上述问题，本发明要提出一种基于Matlab的快速分解法潮流计算方法，可以充分利用Matlab特有的擅长矩阵运算和复数运算的特点，同时又有较快计算速度的潮流计算方法。为了实现上述目的，本发明的技术方案如下：一种基于Matlab的快速分解法潮流计算方法，采用矩阵运算和复数运算；包括以下步骤：A、输入原始数据和初始化电压；电压初始化采用平启动，形成节点电压相量列向量同时形成节点电压幅值列向量V；B、形成节点导纳矩阵；C、记录相关节点类型的节点号；快速分解法修正方程组的方程个数及变量个数与电力系统的节点类型有关，P～θ迭代方程组中没有平衡节点有功功率不平衡量对应的方程和平衡节点相角变量；Q～V迭代方程组中仅有PQ节点无功功率不平衡量对应的方程和PQ节点电压幅值变量。为了提高计算速度，形成方程组系数矩阵及方程右端向量时先不考虑节点类型，形成系数矩阵及方程右端向量后，再去掉无关的行和列。为此，设置两个数组记录有关节点类型的节点号，其中数组bt1记录PQ节点和PV节点的节点号，数组bt2记录PQ节点的节点号。记录相关节点类型的节点号的步骤如下：C1、预定义数组bt的维数为n×1；C2、令k＝1，p＝0；C3、判断节点k是否为平衡节点，如果节点k是平衡节点转至步骤C6；C4、令p＝p+1；C5、令btp＝k；C6、令k＝k+1；C7、判断k是否大于节点数n，如果k不大于n，则返回到步骤C3；否则，转至步骤C8；C8、令数组bt1为数组bt的前p项；C9、令k＝1，p＝0；C10、判断节点k是否为PQ节点，如果节点k不是PQ节点转至步骤C13；C11、令p＝p+1；C12、令btp＝k；C13、令k＝k+1；C14、判断k是否大于节点数n，如果k不大于n，则返回到步骤C10；否则，转至步骤C15；C15、令数组bt2为数组bt的前p项；C16、转至步骤D。D、形成修正方程的系数矩阵B′和B″并进行因子表分解；为了提高计算速度和简化程序，形成系数矩阵B′和B″时不考虑节点类型，都形成n阶方阵，然后再按数组bt1和bt2记录的节点号提取矩阵元素，去掉多余的行和列。按数组bt1记录的节点号提取矩阵B′需要的行和列，去掉平衡节点对应的行和列，形成新的系数矩阵B′；按数组bt2记录的节点号提取矩阵B″需要的行和列，去掉平衡节点和PV节点对应的行和列，形成新的系数矩阵B″。直接调用Matlab软件的LU分解法对系数矩阵B′进行三角分解形成下三角矩阵L1和上三角矩阵U1；对系数矩阵B″进行三角分解形成下三角矩阵L2和上三角矩阵U2。分解后得到的矩阵L1、U1、L2和U2都不包含无关的行和列，在迭代过程解方程时不用再提取矩阵元素。E、形成节点注入有功功率和无功功率向量；潮流计算迭代过程中，计算节点有功功率不平衡量向量和节点无功功率不平衡量向量时，要用到节点注入有功功率列向量Ps和节点注入无功功率列向量Qs，为了提高计算速度，先形成节点注入有功功率向量和节点注入无功功率向量。节点注入有功功率列向量为Ps＝PG-PL(7)式中，Ps为节点注入有功功率列向量；PG为节点发电有功功率列向量；PL为节点负荷有功功率列向量。节点注入无功功率列向量为Qs＝QG-QL(8)式中，Qs为节点注入无功功率列向量；QG为节点发电无功功率列向量；QL为节点负荷无功功率列向量。形成向量Ps和Qs时不考虑节点类型，然后再按数组bt1和bt2记录的节点号提取向量元素，去掉多余的元素。按数组bt1记录的节点号提取向量Ps需要的元素，去掉平衡节点对应的元素，形成新的向量Ps；按数组bt2记录的节点号提取向量Qs需要的元素，去掉平衡节点和PV节点对应的元素，形成新的向量Qs。F、设置迭代计数t＝0，设置收敛标志KP＝0，KQ＝0；G、计算有功功率不平衡量ΔP，并求有功功率最大不平衡量ΔPmax；Matlab擅长矩阵运算和复数运算，因此采用Matlab编程，推导出基于矩阵运算和复数运算的功率计算方法。节点i的复功率公式为式中，为节点i的复功率；Pi和Qi分别为节点i的有功功率和无功功率；为节点电压相量；为节点电流相量的共轭，上标(^)表示复数的共轭。式(9)写成向量相乘的形式为式中，.*表示两向量对应的元素相乘。式(10)中，节点i的电流相量为式(11)代入式(10)，得式中，为节点i的电压相量的共轭值；上标(^)表示复数的共轭。式(12)中最右端向量，写成矩阵与向量乘积形式，得式(13)写成简洁矩阵形式为式中，为节点复功率列向量；为节点电压相量列向量；为节点电压相量的共轭值列向量；Y为导纳矩阵；上标(^)表示复数的共轭；.*表示两向量对应行的元素相乘。节点有功功率P为式中，P为节点有功功率列向量；Re表示取矩阵元素的实部。计算节点有功功率不平衡量的矩阵运算的形成为：式中，ΔP为节点有功功率不平衡量列向量；Ps为节点注入有功功率列向量。求各节点中有功功率不平衡量绝对值最大的值，称为有功功率最大不平衡量，记为ΔPmax。H、判断有功功率最大不平衡量绝对值|ΔPmax|是否小于收敛精度ε；如果小于收敛精度ε，令KP＝1，转到步骤I；否则，解式(17)所示的修正方程，然后按式(18)修正电压相角，计算电压相量列向量令KP＝0，转到步骤J；B'Δθ＝ΔP/V(17)θ(t+1)＝θ(t)-Δθ(t)(18)式中，上标(t)表示第t次迭代的值；Δθ为节点电压相角修正量列向量。使用步骤D形成的下三角矩阵L1和上三角矩阵U1直接调用Matlab软件的解线性方程组算法解修正方程组(17)。I、判断KQ是否等于1；如果KQ＝1，转到步骤N；J、计算无功功率不平衡量ΔQ，并求无功功率最大不平衡量ΔQmax；按式(14)计算节点复功率然后按下式计算节点无功功率Q：式中，Q为节点无功功率列向量；Im表示取矩阵元素的虚部。计算节点无功功率不平衡量矩阵运算的形成为：式中，ΔQ为节点无功功率不平衡量列向量；Qs为节点注入无功功率列向量。求各节点中无功功率不平衡量绝对值最大的值，称为无功功率最大不平衡量，记为ΔQmax。K、判断无功功率最大不平衡量绝对值|ΔQmax|是否小于收敛精度ε；如果小于收敛精度ε，令KQ＝1，转到步骤L；否则，解式(21)所示的修正方程，然后按式(22)修正电压幅值，计算电压相量列向量令KQ＝0，转到步骤M；B"ΔV＝ΔQ/V(21)V(t+1)＝V(t)-ΔV(t)(22)式中，上标(t)表示第t次迭代的值；ΔV为节点电压幅值修正量列向量。使用步骤D形成的三角矩阵L2和U2直接调用Matlab软件的解线性方程组算法解修正方程组(21)。L、判断KP是否等于1；如果KP＝1，转到步骤N；M、令t＝t+1，返回步骤G进行下一次迭代；N、计算平衡节点的有功功率和无功功率及PV节点的无功功率，计算各支路有功功率和无功功率，结束。与现有技术相比，本发明具有以下有益效果：1、本发明提出的方法在Matlab平台实现，便于科研人员使用Matlab提供的各种工具和函数对计算结果进行测试和分析。2、本发明提出的方法采用矩阵运算和复数运算，减少了程序代码，简化了编程，使得程序更加清晰，便于科研人员修改程序、对程序进行调试和改进、添加新功能。3、本发明在LU分解时去掉系数矩阵的无关元素以及在迭代过程前形成节点注入有功功率和无功功率并去掉无关元素，可以避免在迭代过程反复进行提相关矩阵或向量元素的工作，减少了计算工作量，提高了计算速度。4、由于Matlab对矩阵运算实行优化，采用矩阵运算要比按矩阵元素循环运算编程快得多，同时直接调用Matlab的三角分解法方程求解算法，也大大提高了计算速度。实践证明，本发明的方法既方便了科研人员对程序进行编写、修改和调试，同时计算速度也基本接近了在C语言平台上实现的速度，为科研人员的科研工作提供了一个优秀的分析工具。附图说明本发明共有附图3张。其中：图1是现有快速分解法潮流计算的流程图。图2是本发明快速分解法潮流计算的流程图。图3是本发明记录相关节点类型的节点号的流程图。具体实施方式下面结合附图对本发明进行进一步地说明，按照图2-3所示流程对一个修改后的445节点实际系统算例进行了计算。445节点实际大型电力系统有445个节点，544条支路，含有大量的小阻抗支路。为了对各种方法进行比较，把这些小阻抗支路改为正常阻抗支路以满足各种方法的要求。采用本发明和几种对比方法对445节点实际系统算例进行了计算，计算时收敛精度为0.00001。几种潮流计算方法分别为：方法1：中国专利201010585176.X方法，采用Matlab语言实现。方法2：中国专利201010585176.X方法，采用Matlab语言实现，计算节点功率时判断导纳矩阵元素是否为0，导纳矩阵元素为0不计算。方法3：本发明方法。几种方法的计算时间见表1，计算时间不包括数据读入和输出及支路功率计算的时间。表1几种快速分解法潮流计算计算时间比较潮流计算方法计算时间(s)方法188.7881方法22.5083方法30.1487从表1可见，直接采用Matlab实现中国专利ZL201010585176.X方法，计算时间很长；采用Matlab实现专利ZL201010585176.X方法，计算节点功率时判断导纳矩阵元素是否为0，可以大幅度提高计算速度；本发明的计算结果表明采用Matlab的矩阵运算和复数运算，并采用Matlab的三角分解解方程可以有效提高计算速度，同时简化了编程，使程序更加清晰。本发明可以在任何版本的MATLAB编程语言实现，但建议使用较新版本的MATLAB语言。本发明不局限于本实施例，任何在本发明披露的技术范围内的等同构思或者改变，均列为本发明的保护范围。当前第1页1 2 3