一种无位置传感器无刷直流电机的宽速滑模观测器的制作方法

本发明涉及机电控制技术领域，涉及无刷直流电机的无位置传感器控制系统，具体涉及一种无位置传感器无刷直流电机的宽速滑模观测器。

背景技术：

无刷直流电机(Brushless DC Motor，BLDCM)无需电刷便可实现电机定子和转子之间的电气连接，融合了直流电机和交流电机各自的特点，具有控制方式简单、转矩特性高、动态响应快、调速性能良好和制造工艺简单的优势，特别适用于对空间大小有较高要求的场合。

为确保无刷直流电机的正常连续运转，需要通过位置传感器获取转子的位置信息以便进行换相。然而，位置传感器的使用容易受周围环境和条件影响且使用寿命有限，降低了控制系统的可靠性。同时，霍尔位置传感器的存在使得系统的空间占比无法进一步缩小，不利于其在一些空间资源不足的场合发挥作用，也加大了生产和维护的难度，提高了制造成本，限制了制造工艺的进一步提升。

为消除上述位置传感器带来的不利影响，进一步减小控制系统执行机构的成本和空间大小，可采用软硬件结合的技术避免位置传感装置的使用，通过软件算法来提供电机连续换相所需的位置信息，再据此估计出转子速度信息，并将其反馈给控制器实现闭环调速控制。特别是在一些极端环境下，位置检测装置无法正常稳定地工作，无位置传感器控制技术依旧能够确保系统具有良好稳定的控制性能。因此，世界各国各地越来越多的学者和科研人员积极参与到高效稳定且适用广泛的无位置传感器控制技术的研究中来。

通过文献(Position and Speed Control of Brushless DC Motors Using Sensorless Techniques and Application Trends[J].SENSORS,2010,10(7):6901-6947.)可知，目前较常用且相对精准的无位置传感器的转子位置检测方法分为基于反电势检测和基于模型两大类。

基于反电势的检测方法有反电势过零检测法、三次谐波电压积分法、续流二极管检测法和反电势积分法，这些方法都受到速度条件的限制，在低速时性能较差、误差较大且不适用于需要频繁调速系统，或存在无法消除换相误差，易引起误差积累和偏差的问题。

在基于模型的估计方法中，应用最广泛的是状态估计法，主要包括扩展卡尔曼滤波法(EKF)、人工神经网络法(ANN)、模型参考自适应法(MARS)和滑模观测器法(SMO)，适用的速度范围相对更加宽广，但难免存在缺点。扩展卡尔曼滤波具有复杂的算法和结构，限制了其在实际工程中的推广。人工神经网络为了系统参数辨识取得好的结果，常采用在线辨识方式，引入了耗时长和实时性较低的缺点。模型参考自适应法对参数过于敏感，如果参考模型选取不准可能导致系统发散，所以稳定性较差。区别于以上三种方法，很多学者提出了结构简单且便于实现的滑模观测器法，对内部参数和外界扰动有一定的鲁棒性，但鲁棒性依旧有待加强，同时由于滑模结构特点存在无法消除的固有抖振。此外，目前常用的滑模观测器大多只适用于特定速度范围，在速度过低或者过高的条件下存在估计误差较大的缺点。

技术实现要素：

有鉴于此，本发明提供了一种无位置传感器无刷直流电机的宽速滑模观测器，能够扩大滑模观测器的速度适用范围，实现较宽速度范围内的估计，进而实现更宽范围的调速控制。

本发明的无位置传感器无刷直流电机的宽速滑模观测器，将无刷直流电机的参考输入速度分为低速、中速和高速三个速度区间；当无刷直流电机的参考输入速度处于不同速度区间时，所述滑模观测器的滑膜面函数的边界层厚度不同；其中，无刷直流电机的参考输入速度为低速时对应的滑膜面函数的边界层厚度大于中速时对应的滑膜面函数的边界层厚度；无刷直流电机的参考输入速度为高速时对应的滑膜面函数的边界层厚度小于中速时对应的滑膜面函数的边界层厚度。

进一步地，所述低速为：无刷直流电机的参考输入速度小于或等于电机额定转速的30％；所述高速为：无刷直流电机的参考输入速度大于或等于电机额定转速的70％。

进一步地，所述各速度区间所对应的滑膜面函数的边界层厚度为定值。

进一步地，所述中速区间所对应的滑膜面函数的边界层厚度为定值，高速和低速区间所对应的滑膜面函数的边界层厚度为变值。

进一步地，所述各速度区间所对应的滑膜面函数的边界层厚度为变值，所述边界层厚度随着无刷直流电机的参考输入速度的减小而增大。

进一步地，采用神经网络控制器或一维模糊控制器实现所述边界层厚度的自适应变化控制。

进一步地，采用一维模糊控制器进行边界层厚度的自适应变化控制，其中，以无刷直流电机的参考输入速度的绝对值|ω_ref|作为模糊控制器的输入变量，以边界层厚度φ为输出变量；输入变量|ω_ref|和输出变量φ的论域分别选取为{0,0.25,0.5,0.75,1}和{0,0.2,0.4,0.6,0.8,1}，对应的模糊语言子集为{零，正小，正中，正大}；模糊控制规则为：当输入变量|ω_ref|较小时，模糊控制器的输出变量φ较大；当输入变量|ω_ref|较大时，模糊控制器的输出变量φ较小。

进一步地，所述模糊控制规则为：

(1)当输入变量|ω_ref|为零，模糊控制器的输出变量φ为正大；

(2)当输入变量|ω_ref|为正小，模糊控制器的输出变量φ为正中；

(3)当输入变量|ω_ref|为正中，模糊控制器的输出变量φ为正小；

(4)当输入变量|ω_ref|为正大，模糊控制器的输出变量φ为零。

进一步地，采用正弦饱和函数作为滑模面函数。

有益效果：

(1)本发明将无刷直流电机的参考输入速度分为低速、中速和高速三个速度区间，根据直流电机的参考输入速度的不同调整边界层厚度：在低速时增大边界层厚度，有效抑制抖振；在高速时减小边界层厚度，加快观测器响应速度，减小估计误差，从而在整体上提高了滑模观测器准确的观测范围和估计精度，进而获取更好的估计效果和实现更宽范围的调速控制。

(2)可以将各速度区间对应的滑膜面函数的边界层厚度设为定值，调节简单，便于实现；也可以将各速度区间对应的滑膜面函数的边界层厚度设为变值，提高响应精度。

(3)采用正弦饱和函数作为滑模面函数，无需使用低通滤波器即可有效抑制抖振，且收敛速度快、估计精度高。

(4)采用一维模糊控制器实现边界层厚度的自适应变化控制，实现方法简单、鲁棒性强。

附图说明

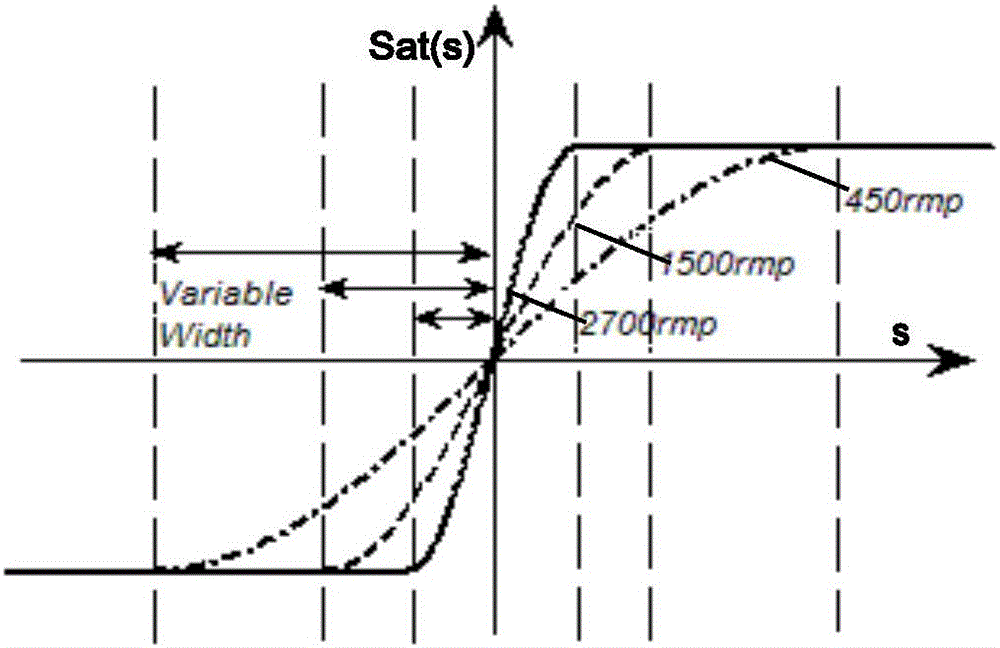
图1为自适应边界层厚度调整示意图。

图2为隶属度函数；(a)输入变量|ω_ref|，(b)输出变量φ。

图3为宽速滑模观测器的结构。

图4为基于宽速滑模观测器的无位置传感器电机系统仿真结构图。

图5为低速下传统滑模观测器速度估计和误差仿真对比图。

图6为低速下宽速滑模观测器速度估计和误差仿真对比图。

图7为高速下传统滑模观测器速度估计和误差仿真对比图。

图8为高速下宽速滑模观测器速度估计和误差仿真对比图。

图9为本发明的宽速滑模观测器估算流程图。

具体实施方式

下面结合附图并举实施例，对本发明进行详细描述。

本发明提供了一种无位置传感器无刷直流电机的宽速滑模观测器，以传统滑模观测器为基础，对无位置传感器无刷直流电机速度控制系统中的滑模观测器进行改进。

在一个无位置传感器控制系统中，传统滑模观测器通常采用Signum函数和Sigmoid函数作为滑模面函数。Signum函数需要配合低通滤波器才能达到抑制抖动的目的，带来严重相位延迟，降低了估计精度。Sigmoid函数相比Signum函数，抑制滑模固有抖振的同时又能够避免低通滤波器使用带来的严重相位延迟，但是却存在以下问题：(1)响应速度变慢且可能造成稳态响应时的脉动，尤其是当滑模观测器需要要求在更宽的速度范围运作时，更加无法保证观测器的快速的响应；(2)传统滑模观测器在设计时会选定参数，然而这些参数仅针对特定速度条件下能取得最好的估计效果，却对不同速度条件缺乏适应性，所以无法在更宽的调速范围下获得精准的估计。

由此，本发明提出一种具有可变边界层滑膜面函数的宽速滑模观测器：所述滑模观测器的滑膜面函数的边界层厚度根据不同的无刷直流电机的参考输入速度进行调节：将无刷直流电机的参考输入速度分为低速、中速和高速三个速度区间，当无刷直流电机的参考输入速度处于不同速度区间时，所述滑模观测器的滑膜面函数的边界层厚度不同；当参考输入速度处于低速时(参考输入速度小于或等于电机额定转速30％)，通过增大边界层厚度来削弱滑模观测器的活动，从而达到有效抑制抖振的目的，进而确保滑模观测器的输出具有良好的稳态性能和准确的估计效果；当参考输入速度处于高速时(参考输入速度大于或等于电机额定转速70％)，通过减小边界层厚度来增强滑模观测器的活动，增强对外部扰动和自身参数变化的鲁棒性，提高响应速度和估计精度。

各速度区间所对应的滑膜面函数的边界层厚度可以为定值；也可以为变值，满足边界层厚度随着参考输入速度的减小而增大的自适应规律。

此外，在实际工程应用中滑模观测器滑膜面函数的边界层厚度不宜过小或过大，厚度过小的边界层会带来严重抖振，反之则会带来很大误差。可通过多次实验和经验找出这两个临界值，限定边界层厚度在有效区间内进行自适应调整。

其中，所述滑膜面函数可以采用传统的Signum函数或Sigmoid函数。本发明采用新型正弦饱和函数代替Signum函数或Sigmoid函数作为观测器的滑模面函数：相比Signum函数，它无需使用低通滤波器即可有效抑制抖振；相比Sigmoid函数，具有更加快速的收敛速度和更高的估计精度。

下面给出一个基于具有可变边界层饱和正弦函数的宽速滑模观测器：

无刷直流电机本身的气息磁场分布、反电势和电流都不是正弦波形式，无需经过直、交轴的坐标系变换，直接利用电机本身的状态变量即可建立数学模型。为了建立电机的数学模型、电磁转矩和运动方程等，以两相通电模式的星形三相六状态电机为例，首先做如下假设：

a)定子上的三相绕组完全对称，空间互差120°电角度，各相参数都相同；

b)忽略磁滞损耗、涡流、铁芯齿槽效应和定子绕组电枢反应等的影响；

c)气隙磁场为方波形式、转子磁场分布都是对称的；

则根据BLDCM的特性，其电压平衡方程

其中，U_a、U_b、U_c是电机定子三相绕组的电压(V)，I_a、I_b、I_c为定子三相的绕组电流(A)，E_a、E_b、E_c是定子三绕组的反电势(V)，L是电机每相绕组的自感(H)，M为两相绕组间的互感，R为定子绕组的电阻(Ω)，P是微分算子。

由于三相电流满足：

I_a+I_b+I_c＝0 (2)

则

MI_a+MI_b＝-MI_c (3)

结合式(1)、式(2)和式(3)，有

考虑电机三相间的对称关系和上述假设成立的情况下，以相电流差和线反电势为状态量，根据式(4)可得到BLDCM的简化数学模型：

其中E_ab和E_bc为定子绕组的两端反电势，U_ab和U_bc为端电压，α＝L-M,β＝R。

根据电机简化的对称数学模型式(5)，可得到以下滑模观测器：

其中x₁＝I_a-I_b，x₂＝I_b-I_c，x₃＝E_ab，x₄＝E_bc，另外ε₁和ε₂是电流观测增益，ε₃和ε₄是反电势观测增益，’^’代表其观测值,Sat(s)是新型正弦饱和函数，表达式如下：

其中θ＝π/2φ，φ是滑模面函数的边界层厚度，并且可以根据不同的参考输入速度自适应调节。

可以采用一个一维模糊控制器来实现新型正弦饱和函数边界层厚度对参考输入速度的自适应策略。从整体上看来，新型正弦饱和函数的边界层厚度随着参考输入速度的减小而增大，示意图可参考图1。同时设计模糊控制器的时候限定边界层厚度，确保其始终处于有效区间，避免引入严重抖振和大的误差。

选取滑模面则定义误差可得到如下所示误差方程：

新型正弦饱和函数自适应调整策略是通过一维模糊控制器实现的，根据ω_ref绝对值的大小对边界层厚度φ进行实时地调整。因为模糊控制器原理简单且实现容易，所以本实施例采用一维模糊控制器实现边界层厚度的自适应调整。在实际应用中只要能够满足该数学规律的一切控制器都可以替代它，例如神经网络控制器等。在此一维模糊控制器中，以参考输入速度的绝对值|ω_ref|作为模糊控制器的输入变量，那么边界层厚度φ即为输出变量。将输入变量|ω_ref|和输出变量φ进行模糊化可分别得到对应的模糊语言变量，然后其论域分别选取为{0,0.25,0.5,0.75,1}和{0,0.2,0.4,0.6,0.8,1}，对应的模糊语言子集则为{Z(零)，PS(正小),PM(正中),PB(正大)}，根据提出边界层厚度自适应调整策略，可以得到如下模糊控制规则：

(1)当输入变量|ω_ref|较小时(正小，零)，模糊控制器的输出变量φ较大(正中，正大)，用较宽的边界层厚度来避免严重抖振；

(2)当输入变量|ω_ref|较大时(正大，正中)，模糊控制器的输出变量φ较小(零，正小)，用较窄的边界层厚度来确保良好的估计精度。

具体的，输入变量|ω_ref|和输出变量φ的隶属度函数如图2所示，模糊控制规则表如表1所示。

表1模糊控制规则表

图3为本发明所提出的宽滑模观测器的结构图，以a-b线反电势为例。其中x₁＝I_a-I_b，x₃＝E_ab，另外ε₁是电流观测增益，ε₃是反电势观测增益，’^’代表其观测值,Sat(s)是新型饱和正弦函数，它的边界层厚度通过一个基于参考输入速度的模糊控制器进行自适应调节。

在Matlab中的仿真结构如图4，主要由以下六个部分组成：电机本体模块(图中的BLDCM)，电流滞环控制模块，速度控制模块(图中的SMC速度控制器)，参考电流模块，电压逆变模块，滑模观测器模块(图中的SMO)。本发明重点部分在于滑模观测器模块，从图中可知它的输入为三相电流、三相电压和参考输入速度，输出是估计的转子位置和速度信号速度，反馈到速度控制器和参考电流模块，构成无位置传感器无刷直流电机闭环控制系统。其他模块的功能和实现可通过相关文献查阅，此处不再详细给出。

为说明本发明提出的宽速滑模观测器具有更宽的观测速度范围，主要考虑在较低和较高两种参考输入速度的情况：低速(900r/mim)和高速(3000r/min)。

图5和图6展示了在低速时传统的滑模观测器和本发明提出的滑模观测器估计的转子速度及稳态时估计误差仿真波形，传统方法的速度估计误差为3.0r/min，本发明滑模观测器误差约为1.5r/min，比传统方法减小了50％左右，有效地提高了估计精度。图7和图8展示参考输入速度在高速时传统的滑模观测器和本发明的滑模观测器估计的转子速度及稳态时估计误差仿真波形的仿真波形。传统方法的速度估计误差为57.0r/min，本发明滑模观测器误差约为16.5r/min，比传统方法减小了71.1％左右，大幅度提高估计精度，同样也有效抑制抖振。

通过在仿真环境中两种方法的对比，可以验证本发明滑模观测器能够在更宽的速度范围下对包括线反电动势、速度和位置在内的状态进行有效且准确的估算。

下面在基于TMS320F28035型MCU的无位置传感器控制实验平台验证本发明中提出的方法。整个无刷直流电机无位置传感器调速控制系统可以分成硬件部分和软件算法部分。控制电路和功率电路组成了硬件的核心部分。软件控制算法是在CCS5.5开发工具中实现，使用C语言进行编程，包括主程序和中断服务程序等，主要重点是本发明提出的滑模观测器估计算法的实现。宽速滑模观测器的算法程序流程如图9所示。

本发明的基于可变边界层厚度的新型正弦饱和函数的宽速滑模观测器，能根据不同速度输入实时调整边界层厚度，确保在更低或者更高速度范围下取得更好的估计效果，进而实现更宽范围的更加精准有效的调速控制。

综上所述，以上仅为本发明的较佳实施例而已，并非用于限定本发明的保护范围。凡在本发明的精神和原则之内，所作的任何修改、等同替换、改进等，均应包含在本发明的保护范围之内。