电压源型换流器高压直流输电附加恒容阻尼控制方法与流程

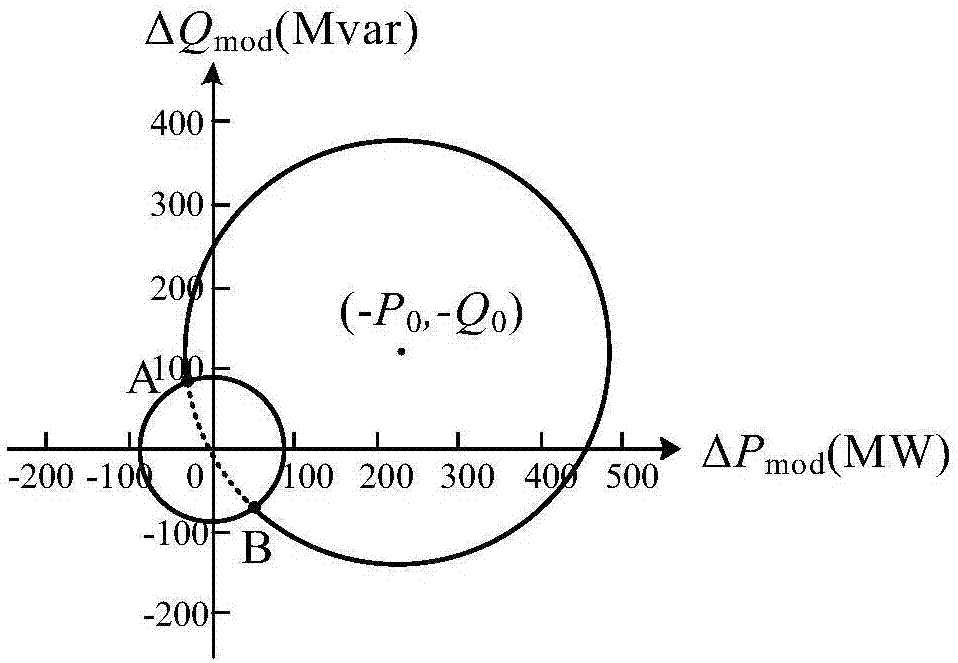
本发明属于高压直流输电领域，尤其是基于暂态能量原理的一种维持换流器传输容量恒定的电压源型换流器高压直流阻尼控制方法。

背景技术：

随着电网规模的日益扩大和直流输电的接入，我国已形成交直流大区互联电力系统，低频振荡对稳定性的影响越来越值得关注。鉴于电压源型换流器高压直流输电(voltage source converter based high voltage direct current transmission，VSC-HVDC)具有有功无功快速独立解耦控制的优势，利用其附加控制抑制电力系统低频振荡变得越来越有实用价值。

目前常用的高压直流附加阻尼控制方法多采用电压源型换流器的有功功率调制来设计附加控制器，没有充分利用到电压源型换流器的调制能力。而电压源型换流器输送容量还较小，因此针对有功参与调制的调制量较小，对于严重故障引起的扰动会显得出力不足且参数协调配合较为复杂。所以，设计一种同时利用系统有功和无功功率进行调制、参数设计简单的附加控制器具有尤为重要的意义。

技术实现要素：

本发明所要解决的技术问题是提供一种电压源型换流器高压直流输电附加恒容阻尼控制方法，在换流站参与功率调制的同时，保证了换流站输送容量的恒定，利于系统稳定运行。

为解决上述技术问题，本发明采用的技术方案是：

一种电压源型换流器高压直流输电附加恒容阻尼控制方法，包括以下步骤：

步骤1：通过基于最小二乘-旋转不变技术的信号参数估计方法对系统进行振荡特性辨识，确定需要抑制的低频振荡模态；

步骤2：检测两区域发电机惯性中心转速差信号ω_AB，对ω_AB取绝对值之后与预设的启动值Δω₀进行比较，若|ω_AB|>Δω₀，则经过一定延时后启动控制器；

步骤3：将ω_AB作为控制器输入信号，ω_AB通过增益环节放大并限幅后作为有功附加调制信号ΔP_mod，将其与原有功整定值P_{I_ref}相叠加作为新的有功整定值P_{I_ref11}；

步骤4：将有功调制信号作为无功调制环节输入，通过式得到的数学逻辑环节来得到无功调制信号ΔQ_mod，将其与原有功整定值Q_{I_ref}相叠加作为新的有功整定值Q_{I_ref11}；P₀、Q₀分别为有功和无功功率整定值，ΔP_mod、ΔQ_mod分别为参与调制的有功和无功功率附加调制信号。

进一步的，所述步骤4具体为：

1)基于暂态能量原理的建模

根据惯性中心坐标下对转子运动方程中的δ_I-II积分得到下式：

定义暂态能量函数：V＝V_P+V_K+V_D＝C；其中，暂态势能函数暂态动能函数阻尼耗散能函数

δ_AB为区域A、B惯性中心角度差；ω_AB为区域A、B惯性中心转子角速度差；M_AB为区域A、B发电机的惯性时间常数；P_mAB为区域A、B间发电机输出机械功率差；P_eAB为区域A、B间发电机输出电磁功率差；D_AB为区域A、B间发电机综合阻尼系数；

2)换流站有功和无功控制规律

系统负荷消耗功率：

式中，P_i0、Q_i0分别为负荷的额定有功功率和无功功率，V_i为母线i的实际电压，V_Ni为母线i的额定电压；定义系统阻尼耗散函数中的D_ABω_AB为从区域A流向区域B的阻尼功率，用流出区域A的阻尼功率和流入区域B的阻尼功率来等效；

设定系统有功功率和无功功率及其调制量的关系满足：

式中，P₀、Q₀分别为VSC2有功和无功功率整定值，ΔP_mod、ΔQ_mod分别为参与调制的有功和无功功率附加调制信号，c为常数；

控制器输出限幅与换流站容量关系为：

式中，η为控制器输出限幅与换流站容量之比；

3)控制器运行区域上有功和无功之间的数学关系

以有功功率调制量ΔP_mod为自变量，对(2)式进行求解，得出无功功率调制量ΔQ_mod的表达式：

进一步的，还包括步骤5：通过数字仿真软件验证控制方法的准确性和有效性。

与现有技术相比，本发明的有益效果是：本发明方法利用换流站参与功率调制的同时，保证换流站输送容量的恒定，利于系统稳定运行；通过数学方法推导出的控制规律不依赖于具体的系统模型，因此具有很好的可移植性；此外，控制器参数设计简单，无需参数协调优化，易于工程实践。

附图说明

图1为恒容阻尼控制器结构图。

图2为恒容阻尼控制器调制功率运行区域。

图3为四机两区域系统结构图。

图4为控制器不同增益k₁下各振荡模态幅值变化曲线。

图5为控制器不同增益k₁下各振荡模态阻尼变化曲线。

图6为母线8单相接地短路时投入恒容阻尼控制器前后区域A、B间惯性中心转子角速度差。

图7为母线8三相接地短路时投入恒容阻尼控制器前后区域A、B间惯性中心转子角速度差。

图8为母线9三相接地短路时投入恒容阻尼控制器前后区域A、B间惯性中心转子角速度差。

具体实施方式

下面结合附图和具体实施方式对本发明作进一步详细的说明。对系统振荡的暂态能量进行分析和建模，从系统暂态能量的消耗机理出发，寻找暂态能量消耗与功率调制的关系，设计恒容阻尼控制器。本发明控制器的控制方法包括以下步骤：

步骤1、对系统进行仿真，检测无扰动情况下两区域发电机的惯性中心转速差信号；并在换流站有功整定值处加0.02倍标幺值的阶跃扰动，再检测两区域发电机的惯性中心转速差信号；以测得的转速差减去无扰动情况下的转速差作为辨识信号，采用最小二乘-旋转不变技术的信号参数估计(TLS-ESPRIT)方法对系统进行振荡特性辨识，得到系统振荡模态信息。

步骤2、检测两区域发电机惯性中心转速差信号ω_AB，对ω_AB取绝对值之后与预设的启动值Δω₀进行比较，若|ω_AB|>Δω₀,则经过一定延时后启动控制器，将ω_AB作为控制器输入信号，ω_AB通过增益环节放大并限幅后作为有功附加调制信号ΔP_mod，将其与原有功整定值P_{I_ref}相叠加作为新的有功整定值P_{I_ref11}。

步骤3、将有功调制信号作为无功调制环节输入，通过以式(4)得到的数学逻辑环节得到无功调制信号Q_mod，将其与原有功整定值Q_{I_ref}相叠加作为新的有功整定值Q_{I_ref11}。

下面通过实例详细阐述本发明方法及其达到的有益效果。

一、基于暂态能量原理的建模分析

根据惯性中心坐标下对转子运动方程中的δ_I-II积分得到下式：

定义暂态能量函数：V＝V_P+V_K+V_D＝C；其中，暂态势能函数暂态动能函数阻尼耗散能函数

式中，δ_AB为区域A、B惯性中心角度差；ω_AB为区域A、B惯性中心转子角速度差；M_AB为区域A、B发电机的惯性时间常数；P_mAB为区域A、B间发电机输出机械功率差；P_eAB为区域A、B间发电机输出电磁功率差；D_AB为区域A、B间发电机综合阻尼系数。

二、换流站有功和无功控制规律

系统负荷消耗功率：

式中，P_i0、Q_i0分别为负荷的额定有功功率和无功功率，V_i为母线i的实际电压，V_Ni为母线i的额定电压。

定义系统阻尼耗散函数中的D_ABω_AB为从区域A流向区域B的阻尼功率，用流出区域A的阻尼功率和流入区域B的阻尼功率来等效。

对于有功功率参与调制的情况，利用直流有功调制构造一个从区域A流向区域B的功率ΔP_dc＝k₁ω_AB,k₁＞0，则ΔP_dc的作用与系统阻尼功率P_D的作用相同，相当于增大了系统的阻尼功率，系统阻尼得到提升。

对于无功功率参与调制的情况，由无功调制产生等效阻尼功率需通过无功与电压的关系来间接实现。从式(1)可以看出，换流站无功调制可提升(增大换流站注入无功时)或降低(减小换流站注入无功时)系统母线电压；系统母线电压升高或降低又会使负荷消耗的有功功率增大或减小。对于环流站VSC2，当换流站产生无功调制量ΔQ_D＝k₂ω_AB,k₂＜0时，系统母线电压将减少(ω_AB＞0时)或增加(ω_AB＜0时)，设此时负荷消耗的功率增量为-D_Bω_AB,D_B＞0，该负荷功率增量可用于等效流入区域B的阻尼功率的作用。即无功调制可产生等效阻尼功率，从而提高系统阻尼。

设想以传输容量恒定作为控制目标，系统有功功率和无功功率及其调制量的关系满足：

式中：P₀、Q₀分别为VSC2有功和无功功率整定值，ΔP_mod、ΔQ_mod分别为参与调制的有功和无功功率附加调制信号，c为常数。

控制器输出限幅与换流站容量关系为：

式中，η为控制器输出限幅与换流站容量之比。

根据(2)式可以画出本文提出的恒容阻尼控制器调制功率的运行范围，如图2中的大圆所示，小圆表示对控制器调制量的限幅。

由式(2)、(3)可求出本文换流器调制输出极限，如图2中的交点A、B，其坐标分别为A(ΔP_min，ΔQ_max)、B(ΔP_max，ΔQ_min)。在系统正常运行情况下，控制器有功和无功调制量均为零；在系统发生故障控制器参与调制的情况下，控制器有功和无功调制量运行在弧所表示的这段区域上。在此区域上有功调制量ΔP_mod和无功调制量ΔQ_mod符号相反，满足各自的阻尼规律。这样，换流站在参与阻尼调制的同时，保持了输送容量恒定。

为进一步描述图2中控制器实际运行区域弧上有功和无功之间的数学关系，以有功功率调制量ΔP_mod为自变量，对(2)式进行求解，得出无功功率调制量ΔQ_mod的表达式：

根据式(4)设计出本发明的恒容阻尼控制器。

三、实际模型仿真

选取标准四机两区域系统作为仿真算例，其结构图如图3所示。其中所有发电机模型均包含励磁及调试系统，VSC1为定直流电压和定无功功率控制，其额定值U_{rec_set}＝320kV，Q_{rec_set}＝-120Mvar；VSC2为定有功功率和定无功功率，其额定值P_{inv_set}＝-200MW，Q_{inv_set}＝-120Mvar。

本发明所设计的控制器中只需对其输出限幅和增益k₁的值进行设置即可。为保证控制器进行无功调制时母线电压变化在相应范围内，将式(3)中η设为30％，并计算出有功和无功限幅值。虽然控制器本身不依赖辨识模型，但可由辨识出的振荡模态选择控制器增益k₁的取值。采用TLS-ESPRIT辨识算法辨识出系统存在三种振荡模态，三种模态具体信息如图4、图5所示。

根据控制器在不同增益下各振荡模态幅值和阻尼比的变化情况可知：系统存在的弱阻尼低频振荡为模态1，其频率为0.51Hz，阻尼比为1.64％。目标模态的阻尼比随着控制器增益k₁的增大而增加，而模态3阻尼比随着k₁增大而降低，两个模态的频率均基本维持恒定。目标模态的阻尼比的提升是以牺牲模态3阻尼比为代价的，但随着k₁的增大模态3的幅值变小，选择模态1、3阻尼比交点附近的增益作为本文控制器的实际增益k₁以保证恰当地阻尼比，在此取k₁＝2。

得到基于电压源型换流器高压直流输电附加恒容阻尼控制器后，在系统中施加不同的扰动与故障，验证控制器的控制性能。仿真的扰动方式为：

1)系统运行第2s时，在母线8设置单相接地短路故障，故障持续0.1s；

2)系统运行第2s时，分别在母线8上加入三相接地短路故障，故障持续0.1s；

3)系统运行第2s时，分别在母线9上加入三相接地短路故障，故障持续0.1s；

根据系统特点和控制目标，选取区域A、B间惯性中心转子角速度差进行观测，并与未加附加阻尼控制器进行对比，如图6-8所示。

仿真结果表明，在不同故障情况下，本发明控制方法均很好地抑制了因交流线路单相接地短路故障引起的系统区间低频振荡，能有效提高系统阻尼。阻尼控制器系统波动较小，传输容量基本维持恒定，可以在保证系统电压稳定的前提下，放宽有功和无功调制容量的限制，将控制器调制能力提升了数倍，使控制器在严重故障时仍能保持良好的控制性能。且控制器只需改变一个增益参数便可实现阻尼控制功能，不需要不同参数之间协调配合，也不依赖于系统特定运行状态对应模型，具有很强的适应性和可移植性。