一种适用于微网的多类型储能多级控制方法与流程

本发明涉及一种微网储能多级控制方法。

背景技术：

由于风光等可再生能源发电的随机性和间歇性，以及负荷波动的不规律性，使得微网的非计划功率变化较大，这给系统的可靠运行带来了很大挑战。而应用储能系统进行微网功率波动的平抑，可以提高系统运行的安全性和稳定性，从而提高电网对可再生能源的消纳。

微网中微源和负荷的波动往往具有多个不同的时间尺度，长时间尺度的波动可以持续数小时或数天，而短时间尺度的波动只有几分钟，甚至几秒钟。因此，单一的储能技术难以同时满足容量和响应速度的要求，需要采用多种性能互补的复合储能平抑微网功率波动。

当前的研究主要侧重于一种功率型储能和一种能量型储能组成的多类型储能，而很少涉及到多种能量型储能及其分配策略。而在实际工程当中，多种能量型储能的联合应用也已出现，在这种复杂的多类型储能系统中，如何协调功率型与能量型，以及多种能量型储能之间的运行，是一个重要课题。因此，需要研究含多种能量型储能和功率型储能的多类型储能系统平抑微网功率波动的控制问题。

中国专利201410391305公开了一种混合储能平抑风电功率波动系统及其协调控制方法，分析风电实际发出的功率和期望功率之间的差额，确定风电平抑所需的有功功率，利用低通滤波方法和模糊控制方法进行有功功率分配，实现蓄电池储能和超级电容器储能的协调控制，但是该专利主要考虑了蓄电池储能和超级电容器储能之间的功率分配，没有考虑不同类型能量型储能内部的功率分配。丁明，林根德，陈自年，等在《中国电机工程学报》2012.32(7):1-6中发表的《一种适用于混合储能系统的控制策略》提出了混合储能运行控制策略，采用时间常数随储能系统荷电状态变化的低通滤波算法确定目标功率值；根据蓄电池和超级电容的荷电状态，采用模糊控制理论将超出目标值的功率偏差在两种储能介质之间进行分配；当超级电容电量充足时，由其独立补偿功率偏差值，以减少蓄电池的充放电次数。但是该文章中提出的控制方法同样没有考虑功率型储能和能量型储能内部的功率分配措施。

技术实现要素：

本发明的目的是克服现有技术的缺点，解决微网中可再生能源发电和负荷功率在不同时间尺度上存在的不同波动特性问题，提出一种适用于微网的多类型储能多级控制方法，以实现功率型储能和能量型电池储能的载荷分配。

本发明通过以下技术方案实现：

本发明控制方法包括波动平抑策略、能量/功率分配策略和经济运行策略等三级控制方法，具体为：首先采用波动平抑策略对微网原始功率进行平滑，获取微网并网功率和储能总载荷曲线；然后在一阶滤波算法的基础上使用基于功率型储能荷电状态的储能充放电分配策略，实现能量型储能和功率型储能之间的功率分配；继而利用基于全寿命周期成本的经济运行策略实现功率型储能内部的功率分配，即超级电容器和飞轮储能的功率分配，同时利用基于度电成本的经济运行策略实现能量型储能内部的功率分配，即锂电池和液流电池的功率分配。

本发明的具体步骤如下：

1、采用模型预测控制算法的波动平抑策略对微网原始功率进行平滑，获取微网并网功率和储能总载荷曲线；

所述的波动平抑策略采用模型预测控制算法，该算法具有较强的应对扰动和不确定性能力，适用于微网功率波动；

所述的模型预测控制算法的核心思想是滚动时域优化策略，滚动时域优化策略包括以下步骤：

(1)在当前时刻k和当前状态x(k)，考虑当前和未来的约束条件，通过优化求解，得到未来k+1，k+2，…k+m时刻的指令序列；

(2)将指令序列的第1个值应用于模型预测算法；

(3)在k+1时刻，更新状态为x(k+1)，重复上述步骤(1)和步骤(2)。

基于所述的模型预测控制算法，通过滚动时域优化策略，可得到微网并网功率和储能总载荷曲线，其具体操作步骤为：

(1)确定微网的并网功率与微网原始功率和储能功率之间的关系，即假设k时刻微网原始功率为pmg(k)，储能功率为pes(k)，则微网的并网功率pg(k)与原始功率pmg(k)、储能功率pes(k)三者之间存在如下关系：

pg(k+1)＝pes(k)+pmg(k)；(1)

(2)确定储能的荷电状态，即假设储能装置控制周期为tc，储能装置总容量为ces，则储能的荷电状态soc,es满足：

soc,es(k+1)＝soc,es(k)-tcpes(k)/ces；(2)

(3)综合考虑储能并网功率与微网原始功率、储能功率关系和储能荷电状态，确定储能平抑微网功率状态空间方程，获取的方法为：将微网的并网功率pg和储能荷电状态soc,es分别作为状态变量x1和x2，储能功率pes作为控制变量u，微网原始功率pmg作为扰动输入量r，pg和soc,es作为输出变量y1和y2，可得到储能平抑微网功率状态空间方程如下：

式(3)中，tc代表储能装置控制周期，k代表k时刻；

(4)确定储能平抑微网功率波动的约束条件；所述的储能平抑微网功率状态空间方程中，储能功率约束条件满足0≤pes(i)≤pes_max，储能荷电状态约束条件满足0≤soc,es(i)≤1，微网并网功率波动率限制约束条件满足

其中，γ为波动率限制值，pes_max为pes(i)的最大值，pes(i)为i时刻储能功率；prated为微网的额定装机容量；pgmax(i)、pgmin(i)分别为pg(i)的最大值和最小值，pg(i)为i时刻微网的并网功率；

(5)利用滚动时域优化策略对微网原始功率进行滚动计算，得到未来k+1，k+2，…k+m时刻的指令序列。通过步骤(4)得到的储能平抑微网功率波动的约束条件对微网原始功率进行约束，可得到满足约束条件的微网并网功率，微网原始功率与微网并网功率的差值为储能总需求功率，将不同时间段的储能总需求功率进行连线处理，即可得到储能总载荷曲线。

2、在一阶滤波算法的基础上采用基于功率型储能荷电状态的储能充放电分配策略，实现能量型储能和功率型储能之间的功率分配，具体步骤为：

(1)通过查询储能总载荷曲线，确定t时刻需求的储能功率，同时，对微网原始数据进行傅里叶分析，确定微网原始数据的主频率，根据该主频率f获取该功率的一阶低通滤波算法时间常数te满足te＝1/2πf。继而，选取一阶低通滤波算法时间常数te对t时刻需求的储能功率进行一阶低通滤波处理，即可确定功率型储能t时刻的充/放电功率。

(2)获取不同时刻下功率型储能的充/放电功率，具体获取方法是：

1)通过改变一阶低通滤波算法时间常数te，判断一阶低通滤波算法对功率型储能荷电状态调节能力，确定一阶低通滤波算法对功率型储能荷电状态调节上下限，其中，soc,p.ess,h为一阶低通滤波算法对功率型储能荷电状态调节上限，soc,p.ess,l为一阶低通滤波算法对功率型储能荷电状态调节下限。

2)将功率型储能储能荷电状态分为5个区域，分别为荷电状态空区(soc,p.ess(t)＝0，soc,p.ess(t)代表t时刻功率型储能的荷电状态)，荷电状态低区(0<soc,p.ess(t)≤soc,p.ess,l)，荷电状态中区(soc,p.ess,l<soc,p.ess(t)<soc,p.ess,h)，荷电状态高区(soc,p.ess,h≤soc,p.ess(t)<100％)和荷电状态满区(soc,p.ess(t)＝100％)。

3)根据不同时刻下(以m时刻为例)功率型储能荷电状态，判断在当前时刻下是否需要调整一阶低通滤波算法时间常数te；如需调整，则重新求取功率型储能的充/放电功率，具体调整方式如下：

a)当荷电状态属于荷电状态空区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为0，若功率型储能处于充电状态，则调整低通滤波时间常数为te(m+1)＝te(m)+△t，其中△t为调整的时间常数，且△t>0；

b)当荷电状态属于荷电状态低区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为te(m+1)＝te(m)-△t，若功率型储能处于充电状态，则调整低通滤波时间常数为te(m+1)＝te(m)+△t；

c)当荷电状态属于荷电状态中区时，不调整一阶低通滤波算法时间常数te；

d)当荷电状态属于荷电状态高区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为te(m+1)＝te(m)+△t，若功率型储能处于充电状态，则调整低通滤波时间常数为te(m+1)＝te(m)-△t；

e)当荷电状态属于荷电状态满区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为te(m+1)＝te(m)+△t，若功率型储能处于充电状态，则功率型储能充电功率设为0。

3、利用基于全寿命周期成本的经济运行策略实现功率型储能内部的功率分配，即超级电容器和飞轮储能的功率分配，具体分配策略如下：

(1)功率型储能全寿命周期成本包括一次投资成本，运行维护成本和回收及环保成本3部分，功率型储能的全寿命周期成本满足：

lcc＝ic+omc+rec(4)

其中，lcc为全寿命周期成本，ic为一次投资成本，omc为运行维护成本，rec为回收及环保成本；

(2)建立功率型储能的经济运行函数，考虑在在1个控制周期内，以功率型储能全寿命周期成本最低为目标函数。由于功率型储能的充放电功率有正有负，所以将储能功率的平方作为功率型储能使用幅度的指标，目标函数f为：

其中，np为功率型储能的种类，包括超级电容器和飞轮储能2类；lcci为第i种功率型储能的度电成本；pi(t)为第i种功率型储能的充放电功率；t0、tc分别为储能作用时的初始时间和结束时间；

(3)确定经济运行的相关约束条件，约束条件为所有储能电池的总出力限制、不同储能电池的充放电限制和荷电状态限制等，具体表达式为：

其中：pi,max和pi,min分别为i种功率型储能的功率上限值和下限值；soc,i为i种功率型储能的荷电状态，soc,i,max和soc,i,min分别为soc,i的上限值和下限值；

(4)在约束条件下对目标函数进行优化求解，实现功率型储能的内部分配，使总体运行成本最低。

4、利用基于度电成本的经济运行策略实现能量型储能内部的功率分配，即锂电池和液流电池的功率分配，具体分配策略如下：

(1)根据不同储能电池的成本特性，考虑以充放电1kw·h的电量为基准，结合其初始投资、循环寿命以及充放电深度等特性，定义不同储能电池的度电成本，储能电池的度电成本满足：

其中，cost为电池的度电成本；n为循环寿命；dod为电池充放电深度，omc为运行维护成本；

(2)建立能量型储能电池的经济运行函数，考虑在在1个控制周期内，以储能电池总的度电成本最低为目标函数。由于电池的充放电功率有正有负，所以将储能功率的平方作为电池使用幅度的指标，目标函数f为：

其中，nb为电池的种类，包括液流电池和锂电池2类；cost,i为第i种电池的度电成本；p1i(t)为第i种电池的充放电功率；t0、tc分别为储能作用时的初始时间和结束时间；

(3)确定经济运行的相关约束条件，约束条件为所有储能电池的总出力限制、不同储能电池的充放电限制和荷电状态限制等，具体表达式为：

其中：p1i,max和p1i,min分别为i种电池的功率上限值和下限值；soc,1i为i种电池的荷电状态，soc,1i,max和soc,1i,min分别为soc,1i的上限值和下限值；

(4)在约束条件下对目标函数进行优化求解，实现能量型储能的内部分配，使总体运行成本最低。

附图说明

图1为多类型储能协调控制原理图；

图2为储能载荷的确定方法框图；

图3为能量型和功率型储能的载荷分配控制框图；

图4为多种功率型储能的载荷分配控制框图；

图5为多种能量型储能的载荷分配控制框图；

图6为多级控制策略流程图；

图7为平抑前后微网功率时域图；

图8为平抑前后1min波动率；

图9为平抑前后30min波动率；

图10为综合储能、能量型储能和功率型储能功率分配曲线；

图11为功率型储能电池载荷经济分配曲线；

图12为能量型储能电池载荷经济分配曲线。

具体实施方式

以下结合图和具体实施方式对本发明作进一步说明。

图1为多类型储能协调控制原理图。图1中，pmg为微网的原始功率，pg为微网的并网功率，pes为总储能功率，pp.ess为功率型储能功率，pw.ess为能量型储能功率，psc为超级电容器功率，pfess为飞轮储能功率，pvrb为液流电池储能功率，pli为锂电池储能功率。

本发明包括以下步骤：

1、采用模型预测控制算法的波动平抑策略对微网原始功率进行平滑，获取微网并网功率和储能总载荷曲线；

所述的波动平抑策略采用模型预测控制算法。如图1所示，当微网原始功率输入后，基于所述的模型预测控制算法，通过滚动时域优化策略，可得到微网并网功率和储能总载荷曲线。

所述模型预测控制算法的核心思想是滚动时域优化策略，滚动时域优化策略包括以下步骤：

(1)在当前时刻k和当前状态x(k)，考虑当前和未来的约束条件，通过优化求解，得到未来k+1，k+2，…k+m时刻的控制序列；

(2)将控制指令序列的第1个值应用于模型预测算法；

(3)在k+1时刻，更新状态为x(k+1)，重复上述步骤(1)和步骤(2)。

所述的储能总载荷曲线即为在不同时刻下储能总功率需求的连线。

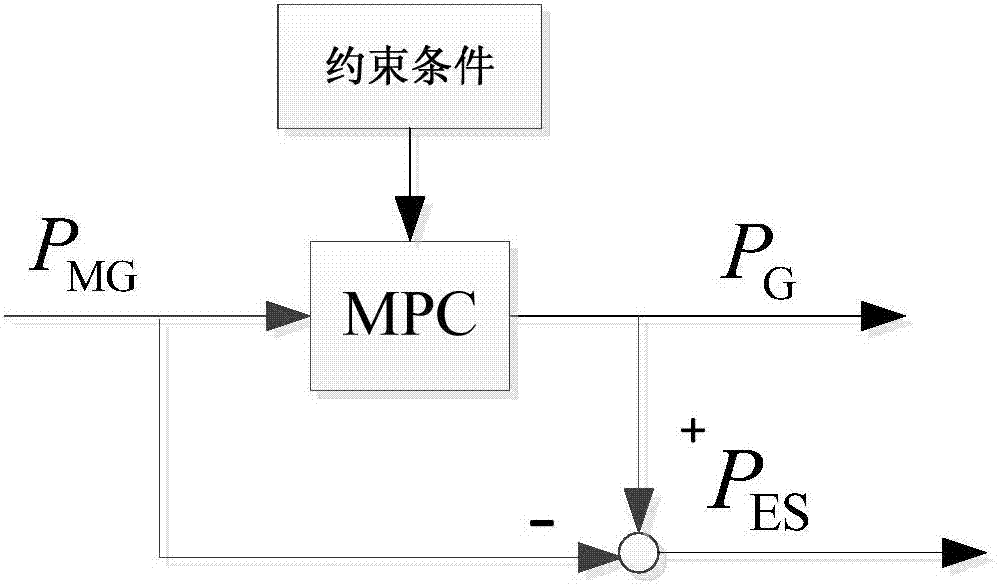
图2为储能总载荷曲线的确定方法框图。图2中，mpc为模型预测控制算法，约束条件包括储能功率约束条件、储能荷电状态约束条件和微网并网功率波动率限制。

储能功率约束条件满足0≤pes(i)≤pes_max，其中，pes(i)为i时刻的储能功率，pes_max为pes(i)的最大值。

储能荷电状态约束条件满足0≤soc,es(i)≤1，其中，soc,es(i)为i时刻的储能荷电状态。

微网并网波动率限制满足其中，γ为波动率限制值，选择的波动率限制值为波动率限制条件为1min内≤2％和30min内≤7％。prated为微网的额定装机容量；pgmax(i)、pgmin(i)分别为pg(i)的最大值和最小值，pg(i)为i时刻微网的并网功率。

储能总载荷曲线的确定包括以下步骤：

(1)确定微网的并网功率与微网原始功率和储能功率之间的关系，即假设k时刻微网原始功率为pmg(k)，储能功率为pes(k)，则微网的并网功率pg(k)与原始功率pmg(k)、储能功率pes(k)三者之间满足pg(k+1)＝pes(k)+pmg(k)；

(2)综合考虑储能并网功率与微网原始功率、储能功率关系和储能荷电状态，确定储能平抑微网功率状态空间方程，将微网的并网功率pg和储能荷电状态soc,es分别作为状态变量x1和x2，储能功率pes作为控制变量u，微网原始功率pmg作为扰动输入量r，pg和soc,es作为输出变量y1和y2，可得到储能平抑微网功率状态空间方程为：

其中，tc代表储能装置控制周期，k代表k时刻。

(3)利用滚动时域优化策略对微网原始功率进行滚动计算，得到未来k+1，k+2，…k+m时刻的控制序列。通过储能平抑微网功率波动的约束条件对微网原始功率进行约束，可得到满足约束条件的微网并网功率，微网原始功率与微网并网功率的差值为储能总需求功率，将不同时间段的储能总需求功率进行连线处理，即可得到储能总载荷曲线。

2、得到储能总载荷曲线后，在一阶滤波算法的基础上使用基于超级电容器荷电状态的储能充放电分配策略，实现能量型储能和功率型储能之间的功率分配。所分配的功率型储能功率通过经济运行策略进行分配，分别得到超级电容器功率和飞轮储能功率，并将相应的功率分别输送给超级电容器和飞轮储能，控制超级电容器和飞轮储能输出相应功率；所分配的能量型储能功率通过经济运行策略进行分配，分别得到液流电池储能功率和锂电池储能功率，并将相应的功率分别输送给液流电池和锂电池，控制液流电池和锂电池发出相应功率。

图3为能量型储能和功率型储能的载荷分配控制框图，图3中，soc,p.ess,lim为超级电容器储能的荷电状态限制值，psc,lim为功率限制值。考虑到超级电容器具有充放电速率快、循环寿命长等优点，基于超级电容器荷电状态的充放电原则来实现超级电容器和蓄电池之间的载荷分配。

能量型储能和功率型储能的载荷分配控制方法包括以下步骤：

(1)通过查询储能总载荷曲线，确定t时刻需求的储能功率，同时，对微网原始数据进行傅里叶分析，确定微网原始数据的主频率，根据该主频率f获取该功率的一阶低通滤波算法时间常数te满足te＝1/2πf。继而，选取一阶低通滤波算法时间常数te对t时刻需求的储能功率进行一阶低通滤波处理，确定功率型储能t时刻的充/放电功率。

(2)获取不同时刻下功率型储能的充/放电功率，具体获取方法是：

1)通过改变一阶低通滤波算法时间常数te，判断一阶低通滤波算法对功率型储能荷电状态调节能力，确定一阶低通滤波算法对功率型储能荷电状态调节上下限，其中，soc,p.ess,h为一阶低通滤波算法对功率型储能荷电状态调节上限，soc,p.ess,l为一阶低通滤波算法对功率型储能荷电状态调节下限。

2)将功率型储能储能荷电状态分为5个区域，分别为荷电状态空区(soc,p.ess(t)＝0，soc,p.ess(t)代表t时刻功率型储能的荷电状态)，荷电状态低区(0<soc,p.ess(t)≤soc,p.ess,l)，荷电状态中区(soc,p.ess,l<soc,p.ess(t)<soc,p.ess,h)，荷电状态高区(soc,p.ess,h≤soc,p.ess(t)<100％)和荷电状态满区(soc,p.ess(t)＝100％)。

3)根据不同时刻下功率型储能荷电状态，判断在当前时刻下是否需要调整一阶低通滤波算法时间常数te；如需调整，则重新求取功率型储能的充/放电功率，以m时刻为例说明具体调整方式如下：

a)当荷电状态属于荷电状态空区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为0，若功率型储能处于充电状态，则调整低通滤波时间常数为te(m+1)＝te(m)+△t，其中△t为调整的时间常数，且△t>0；

b)当荷电状态属于荷电状态低区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为te(m+1)＝te(m)-△t，若功率型储能处于充电状态，则调整低通滤波时间常数为te(m+1)＝te(m)+△t；

c)当荷电状态属于荷电状态中区时，不调整一阶低通滤波算法时间常数te；

d)当荷电状态属于荷电状态高区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为te(m+1)＝te(m)+△t，若功率型储能处于充电状态，则调整低通滤波时间常数为te(m+1)＝te(m)-△t；

e)当荷电状态属于荷电状态满区时，判断m时刻功率型储能状态，若功率型储能处于放电状态，则功率型储能放电功率设为te(m+1)＝te(m)+△t，若功率型储能处于充电状态，则功率型储能充电功率设为0。

4)确定不同时刻下，能量型储能的充/放电功率，以i时刻能量型储能的充/放电功率获取为例，具体获取方法是：将i时刻的储能总需求功率与i时刻的超级电容器充/放电功率取差即可得到i时刻的能量型电池储能充/放电功率。

3、在得到功率型储能和能量型储能充/放电功率后，利用基于全寿命周期成本的经济运行策略实现功率型储能内部的功率分配，即超级电容器和飞轮储能的功率分配。

图4为多种功率型储能的载荷分配控制框图，图4中，σpi为第i种功率型储能总的充/放电功率，soc,sc,lim和psc,lim分别为超级电容器的荷电状态和功率限制,soc,fess,lim和pfess,lim分别为飞轮储能的荷电状态和功率限制。

多种功率型储能载荷的具体分配策略如下：

1)功率型储能全寿命周期成本包括一次投资成本，运行维护成本和回收及环保成本3部分，功率型储能的全寿命周期成本满足：

lcc＝ic+omc+rec

其中，lcc为全寿命周期成本，ic为一次投资成本，omc为运行维护成本，rec为回收及环保成本。

2)建立功率型储能的经济运行函数，考虑在在1个控制周期内，以功率型储能全寿命周期成本最低为目标函数。由于功率型储能的充放电功率有正有负，所以将储能功率的平方作为功率型储能使用幅度的指标，目标函数f为：

其中，np为功率型储能的种类，包括超级电容器和飞轮储能2类；lcci为第i种功率型储能的度电成本；pi(t)为第i种功率型储能的充放电功率；t0、tc分别为储能作用时的初始时间和结束时间；

3)确定经济运行的相关约束条件，约束条件为所有储能电池的总出力限制、不同储能电池的充放电限制和荷电状态限制等，具体表达式为：

其中：pi,max和pi,min分别为i种功率型储能的功率上限值和下限值；soc,i为i种功率型储能的荷电状态，soc,i,max和soc,i,min分别为soc,i的上限值和下限值；

4、利用基于度电成本的经济运行策略实现能量型储能内部的功率分配，即锂电池和液流电池的功率分配；

图5为多种能量型电池储能的载荷分配控制框图，图5中，σp1i为第i种电池总的充放电功率，soc,v,lim和pv,lim分别为液流电池的荷电状态和功率限制,soc,l,lim和pl,lim分别为锂电池的荷电状态和功率限制。

多种能量型电池储能的载荷分配控制具体步骤如下：

(1)根据不同储能电池的成本特性，考虑以充放电1kw·h的电量为基准，结合其初始投资、循环寿命以及充放电深度等特性，定义不同储能电池的度电成本，储能电池的度电成本满足：

其中，cost为电池的度电成本；n为循环寿命；dod为电池充放电深度，omc为运行维护成本；

(2)建立能量型储能电池的经济运行函数，考虑在在1个控制周期内，以储能电池总的度电成本最低为目标函数。由于电池的充放电功率有正有负，所以将储能功率的平方作为电池使用幅度的指标，目标函数f为：

其中，nb为电池的种类，包括液流电池和锂电池2类；cost,i为第i种电池的度电成本；p1i(t)为第i种电池的充放电功率；t0、tc分别为储能作用时的初始时间和结束时间；

(3)确定经济运行的相关约束条件，约束条件为所有储能电池的总出力限制、不同储能电池的充放电限制和荷电状态限制等，具体表达式为：

其中：p1i,max和p1i,min分别为i种电池的功率上限值和下限值；soc,1i为i种电池的荷电状态，soc,1i,max和soc,1i,min分别为soc,1i的上限值和下限值；

(4)在约束条件下对目标函数进行优化求解，实现能量型储能的内部分配，使总体运行成本最低。

对适用于微网的多类型储能多级控制方案的控制流程进行梳理，可得到图6所示的多级控制策略流程图，具体控制流程为：

(1)输入实测微网功率数据；

(2)根据并网波动率要求，利用模型预测控制算法求取储能总载荷和并网功率；

(3)根据功率型储能的荷电状态和充放电功率限制，利用功率型储能优先充放电的控制策略求取能量型储能和功率型储能的载荷；

(4)利用基于全寿命周期成本的经济运行策略实现功率型储能内部的功率分配，即超级电容器和飞轮储能的功率分配；

(5)利用基于度电成本的经济运行策略实现能量型储能内部的功率分配，即锂电池和液流电池的功率分配。

以实际案例对适用于微网的多类型储能多级控制方案进行验证。

图7为平抑前后微网功率时域图，采用波动率限制条件为1min内≤2％和30min内≤7％。在该并网波动率限制下，采用模型预测控制算法对微网功率数据进行仿真分析，如图6所示。对比分析平抑前后的微网功率可以发现，平抑后的微网功率波动较小，平滑效果相对显著。

图8为平抑前后1min波动率，由图7可以看出，在平抑前，微网功率波动率最大值在6％，不满足1min波动率要求，平抑后的微网功率波动率得到了有效改善，其1min的波动率<2％，满足并网波动率要求。

图9为平抑前后30min波动率，由图8可以看出，在平抑前，微网功率波动率最大值在18％，不满足30min波动率要求，平抑后的微网功率波动率得到了有效改善，其30min的波动率<7％，满足并网波动率要求。

图10为综合储能、能量型储能和功率型储能功率分配曲线，其中，第一个图为综合储能功率曲线，第二个图为能量型储能功率曲线，第三个图为功率型储能功率曲线。综合储能、能量型储能和功率型储能分配曲线获取方法为将模型预测控制算法求得的储能总载荷曲线利用基于超级电容器荷电状态的储能充放电分配策略进行处理。当超级电容器荷电状态较高时，提高放电减少充电；当其荷电状态较低时，提高充电减少放电。通过滤波常数的调整，优先获取超级电容器功率型储能载荷曲线，即可获取能量型储能载荷曲线。图10中变化较慢的功率由能量型储能吸收，变化较快的功率由功率型储能吸收，使多类型储能的高能量密度和高功率密度特性得到有效发挥。

图11为功率型储能载荷经济分配曲线，功率型储能主要包括超级电容器和飞轮储能。根据设定的参数求取两种功率型储能的全寿命周期成本，超级电容器的功率成本约为500元/kw，飞轮储能的功率成本约为1700元/kw，两种功率型储能成本由低到高的排序为超级电容器<飞轮储能。

图11的功率型储能载荷经济分配曲线可以看出，功率型储能的载荷首先由全寿命周期成本较低的超级电容器承担，其承担了较大部分的功率输出；当其自身不能满足储能功率要求时，超出的功率部分按照全寿命周期成本从低到高的顺序由飞轮储能承担，从而使得功率型储能的总体经济成本最低。

图12为能量型储能载荷经济分配曲线，能量型储能主要包括液流电池和锂电池。根据设定的参数求取储能电池的度电成本，每种电池的度电成本和功率数值等参数如下表所示。

表1液流电池和锂电池度电成本特性

根据表1中2种电池的度电成本特性可以看出，2种电池成本由低到高的排序为：液流电池<锂电池。

图12的能量型储能载荷经济分配曲线可以看出，能量型储能的载荷首先由度电成本较低的液流电池承担，其承担了较大部分的功率输出；当其自身不能满足储能功率要求时，超出的功率部分按照度电成本从低到高的顺序由锂电池承担，从而使得能量型储能的总体经济成本最低。