对称式LCC谐振网络的ECPT系统及其参数设计方法与流程

本发明涉及无线电能传输技术领域，具体涉及一种对称式LCC谐振网络的ECPT系统及其参数设计方法。

背景技术：

无线电能传输技术(Wireless Power Transfer，WPT)是一种综合利用了现代电力电子技术、磁场(电场)耦合技术和现代控制理论来实现电能无线传输的技术，该技术已成为全球的研究热点，世界经济论坛(WEF)也连续两年将无线电能传输技术列为对世界影响最大、最有可能为全球面临的挑战提供答案的十大新兴技术之一。它解决了传统导线直接电气接触带来的各种问题，具有广泛的应用前景。其中以感应耦合电能传输技术(Inductively Coupled Power Transfer，ICPT)的研究最为热门，也取得了众多的理论和实际成果，并逐步推广应用。

作为近年来提出的一种基于电场耦合式无线电能传输(Electric-Field Coupled Power Transfer，ECPT)技术，以电场作为能量传输媒介，电能耦合机构简易轻薄，形状易变；在工作状态中，电场耦合机构的绝大部分电通量分布于电极之间，对周围环境的电磁干扰很小；当电场耦合机构之间或周围存在金属导体时，不会引起导体产生涡流损耗。从ECPT技术的上述特点可以看出其具有广阔的发展前景，因此也越来越受到国内外专家和学者的关注。目前，对于ECPT系统，已在LED灯、无线鼠标、移动电话、生物电测量以及电动汽车充电等方面展开了研究，也取得了众多研究成果。

传统的ECPT系统由于耦合极板容值过小，通常需要串联较大电感来补偿其容抗，从而导致系统体积和质量增大，且电感等效串联电阻较大，损耗增加。一般通过增大系统工作频率或耦合极板容值，以减小串联补偿电感，从而达到增大传输功率和传输效率的目的。然而频率高达上兆赫兹的系统，开关管损耗必然会增大，而且系统控制难度也大大增加。而增大耦合极板容值则致使耦合极板面积增大或传输距离变小，也使得ECPT系统应用受限。

技术实现要素：

本申请通过提供一种对称式LCC谐振网络的ECPT系统及其参数设计方法，在不需要大幅度增加系统频率和串联补偿电感的条件下，就可以实现传输距离大、传输效率高的效果，同时也提高了系统鲁棒性，提升了系统功率密度，降低了应用成本。

为解决上述技术问题，本申请采用以下技术方案予以实现：

一种对称式LCC谐振网络的ECPT系统，其特征在于，包括直流电源、高频逆变电路、LC补偿网络、由两对耦合极板构成的耦合单元、CL补偿网络、整流滤波电路以及负载电阻R_L，其中，所述直流电源经由所述高频逆变电路转换为高频交流电，所述LC补偿网络由电感L₁以及电容C₁构成，所述电感L₁的一端连接所述高频逆变电路的第一输出端，所述电感L₁的另一端连接一块发射极板以及所述电容C₁的一端，所述电容C₁的另一端连接另一块发射极板以及所述高频逆变电路的第二输出端，所述CL补偿网络由电感L₂以及电容C₂构成，在所述电容C₂的两端各自连接有一块接收极板，发射极板与接收极板一一对应耦合实现能量无线传输，电容C₂的一端与所述整流滤波电路的第一输入端连接，电容C₂的另一端与所述谐振电感L₂连接，所述电感L₂的另一端与所述整流滤波电路的第二输入端连接，在所述整流滤波电路的两个输出端之间连接所述负载电阻R_L。

进一步地，为了满足参数对称关系，C₁＝C₂，L₁＝L₂。

一种对称式LCC谐振网络的ECPT系统的参数设计方法，包括如下步骤：

S1：根据应用场景的需求来确定该系统的工作频率f，耦合单元等效电容C_s以及负载电阻R_L；

S2：根据下面公式计算系统参数：

所述谐振电感式中，k₁＝k₂＝k，k₁＝C₁/C_s，k₂＝C₂/C_s，ω为系统基波角频率；

当时，系统工作于ZPA状态，式中，品质因数Q＝ωL₂/R_eq，R_eq为等效交流电阻，且R_eq＝8R_L/π²；

所述谐振电容

根据需要选择最低次谐波分量(其角频率为ω_min)，并确定与之对应的电压幅值增益上限k_min，即|T(jω_min)|≤k_min≤|T(jω)|，也即

S3：利用系统谐振工作点函数验证系统参数和系统鲁棒性：

S31：建立系统状态空间模型；

S32：建立系统频闪映射模型；

S33：分析系统参数变化对系统谐振工作点的影响。

进一步地，步骤S31中建立的系统状态空间模型为：

其中，

式中，x＝[i₁ u₁ u₂ u_s i₂]^T为该系统的状态向量，u＝[u_i]为该系统的输入向量，为谐振电感L₁的等效串联电阻，为谐振电感L₂的等效串联电阻，为耦合单元等效电容C_s的等效串联电阻，tanδ为介质损耗角正切值。

进一步地，建立系统频闪映射模型包括以下步骤：

S321：将建立的状态空间模型分段线性化为两个模态：

模态1：开关管S₁和S₄导通，开关管S₂和S₃关断，系统的输入变量u_i＝E；

模态2：开关管S₁和S₄关断，开关管S₂和S₃导通，系统的输入变量u_i＝-E；

E为系统输入电压；

S322：两个模态的持续时间分别为半个周期T/2，在模态1和模态2下该系统的状态映射函数如下：

S323：假设第n个稳态周期的初始状态为x_n，第n个稳态周期的结束状态为x_n+1，当系统处于稳态时，系统的状态向量周期性的重复，即有x_n+1＝x_n，建立系统第n个稳态周期的频闪映射模型：

式中，Φ(t)＝e^At；

S324：得到系统的稳态周期不动点x*：

S325：定义Y＝[10000]为系统的状态选择矩阵，取出不动点x^*中的电流分量，得到用于分析谐振软开关工作点的系统周期不动点函数：

进一步地，步骤S3中利用系统谐振工作点函数方程对参数进行验证，若满足条件，则给出确定的系统参数；若不满足条件，则微调系统频率f，使系统参数满足函数方程同时，通过求解系统谐振工作点函数方程可得到系统谐振软开关工作点随各参数的变化曲线，由此可说明系统鲁棒性问题。

作为一种优选的参数配置方法，在步骤S1中，该系统的工作频率f＝500kHz，耦合单元等效电容C_s＝30pF以及等效交流电阻R_eq＝40Ω。

与现有技术相比，本申请提供的技术方案，具有的技术效果或优点是：通过提供一种对称式LCC谐振网络的ECPT系统及其参数设计方法，在不需要大幅度增加系统频率和串联补偿电感的条件下，就可以实现传输距离大、传输效率高的效果，同时也提高了系统鲁棒性，提升了系统功率密度，降低了应用成本。

附图说明

图1为对称式LCC谐振网络的ECPT系统原理图；

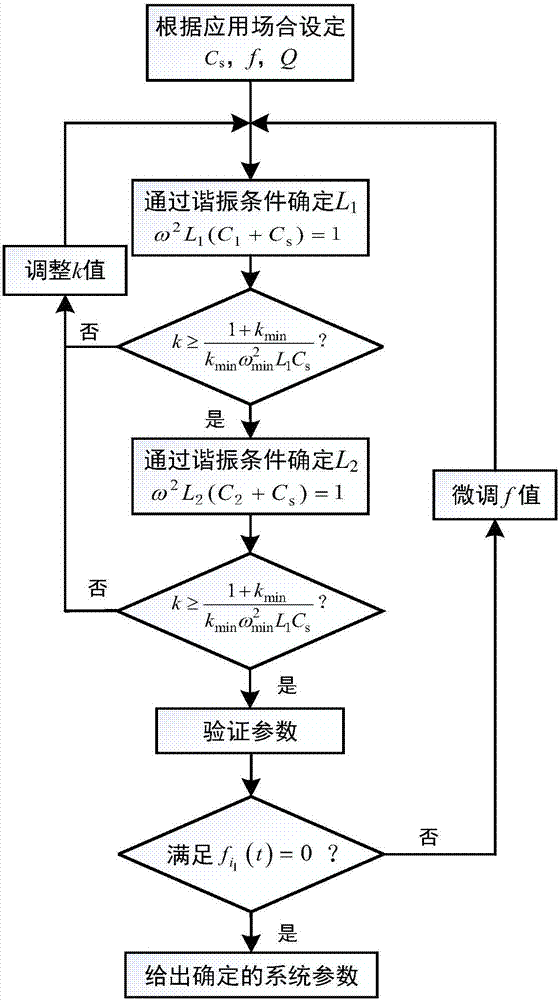
图2为系统参数设计流程图；

图3为ECPT系统等效电路；

图4为ECPT系统实际电路原理图；

图5为逆变器输出电流周期不动点函数曲线图；

图6(a)为谐振工作点随负载变化图；

图6(b)为谐振工作点随耦合极板电容变化图；

图6(c)为谐振工作点随L₁和L₂变化图；

图6(d)为谐振工作点随C₁和C₂变化图；

图7为逆变输出电压和电流关系曲线图；

图8为系统输入电压和极板激励电压关系曲线图；

图9为负载切换下系统输出电流图；

图10为逆变输出电压和电流波形图；

图11为系统输入电压和极板激励电压波形图；

图12为激励电压和负载拾取电压波形图；

图13为P_out和η随C_s的变化曲线图。

具体实施方式

本申请通过提供一种对称式LCC谐振网络的ECPT系统及其参数设计方法，在不需要大幅度增加系统频率和串联补偿电感的条件下，就可以实现传输距离大、传输效率高的效果，同时也提高了系统鲁棒性，提升了系统功率密度，降低了应用成本。

当传输距离增大时，若极板尺寸和系统频率保持不变，耦合电容C_s的值则减小，对于传统的ECPT系统而言，需要串联较大的电感来补偿其容抗，因此导致损耗增加，体积和成本也相应增加。为解决上述问题，本发明将C_s引入LC网络中构成LCC谐振网络进行分析，用L补偿两并联电容容抗之和。通过使C₁的值增大，使C_s的值减小或保持不变来增大两电容之和，既能保证传输距离较大，又能减小L的值，减小电感损耗。为进一步减小开关管损耗以提高传输效率，同时减弱电磁干扰，降低系统工作频率至500KHz。此外，通过对称的参数设计，使系统工作于ZPA状态，增大了系统功率因数。为了更好的理解上述技术方案，下面将结合说明书附图以及具体的实施方式，对上述技术方案进行详细的说明。

实施例

如图1所示，一种对称式LCC谐振网络的ECPT系统，包括直流电源、高频逆变电路、LC补偿网络、由两对耦合极板构成的耦合单元、CL补偿网络、整流滤波电路以及负载电阻R_L，其中，所述直流电源经由所述高频逆变电路转换为高频交流电，所述LC补偿网络由电感L₁以及电容C₁构成，所述电感L₁的一端连接所述高频逆变电路的第一输出端，所述电感L₁的另一端连接一块发射极板以及所述电容C₁的一端，所述电容C₁的另一端连接另一块发射极板以及所述高频逆变电路的第二输出端，所述CL补偿网络由电感L₂以及电容C₂构成，在所述电容C₂的两端各自连接有一块接收极板，发射极板与接收极板一一对应耦合实现能量无线传输，电容C₂的一端与所述整流滤波电路的第一输入端连接，电容C₂的另一端与所述谐振电感L₂连接，所述电感L₂的另一端与所述整流滤波电路的第二输入端连接，在所述整流滤波电路的两个输出端之间连接所述负载电阻R_L。

系统工作原理：

LC补偿网络与耦合极板等效电容C_s构成正向LCC谐振网络，耦合极板等效电容C_s与CL补偿网络构成反向LCC谐振网络。能量发射端首先由直流电源输入高频逆变电路(或由供电电网输入的工频交流电经整流后输入给高频逆变电路)，高频逆变电路将直流电转换为高频交流电输出，经LC补偿网络后提供给发射极板，发射极板与接收极板在交互电场的作用下产生位移电流，实现极板之间能量的传输。通过在能量接收端引入CL补偿网络，以减小极板上的无功功率，同时提高传输效率，最后输出交流电经整流滤波后为负载电阻R_L供能。

为了便于分析，本发明采用基波近似简化系统，且认为所有元件均为理想元件。ECPT系统等效电路如图3所示，图中u_i为逆变输出方波电压的基波分量，R_eq为等效交流电阻，R_eq＝8R_L/π²。

对由L₁、C₁和C_s构成的正向LCC谐振网络，根据基尔霍夫电压定律有：

式中，为电压源输入电压，为谐振电容C₁两端电压，为谐振电容C₂两端电压，也即正向LCC网络输出电压，和分别为流过谐振电感L₁和耦合极板等效电容C_s的电流，ω为基波角频率，由公式1可得：

式中，k₁＝C₁/C_s，令公式2的虚部为零，即得到谐振电感L₁的参数设计：

由公式3可知，L₁实际上补偿C₁与C_s的容抗之和，可见只需通过设计合适的C₁和C_s既可保证耦合极板尺寸无需很大，距离也不会太小(即耦合极板等效电容可以很小)，也能保证L₁的值不会太大，避免了传统ECPT系统中因为耦合极板容值过小而必须串联较大电感来补偿其无功，从而减小了电感等效内阻损耗，提高传输效率。

结合公式2和公式3，则有

联立公式3和公式4可得

由公式5可知，LCC网络输出电压仅由输入电压决定，与后级电路结构和特性无关，且不管后级电路如何变化，LCC网络的输出电压最终都能够自动调节到变化前的状态。同时也可以看出，LCC网络有电压倍增作用，且输出电压与输入电压同相位。

由上述分析可知，流过R_eq的电流为：

由公式6可得：

公式7中U₂和I₂分别为和的有效值，由公式7可以看出，针对本发明所提ECPT系统，当负载电阻在百欧姆以内时，满足Q²＞＞1(Q为品质因数，且Q＝ωL₂/R_eq)，则

可见系统表现出恒流输出特性。

对由L₂、C₂和C₂构成的反向LCC谐振网络，分析原理与上述正向LCC相同，可得：

式中，k₂＝C₂/C_s，为等效交流电阻R_eq两端电压。可见R_eq两端电压与C₁两端电压同相位，同时系统在后级反向LCC的作用下实现了从耦合极板激励电压到输出电压的降压作用，降压倍数可以通过设置C₂值灵活变化。对输出电压，也有

若k＝k₁＝k₂，可以求得C₁＝C₂，L₁＝L₂，即满足参数对称关系，由公式5、6、9、10可得：

即为耦合极板激励电压，为使耦合极板两端电压不至于过高而产生安全隐患，可以通过设置合适的k值来改变激励电压的大小。

又由公式11可得：

所以电路输入阻抗为：

且有

式中，为输入电压和电流的相位角之差。由公式14可知，随Q值增大而增大，当时，此时输入电压和电流同相位，即系统实现ZPA工作。

进一步地，为了满足参数对称关系，C₁＝C₂，L₁＝L₂。

一种对称式LCC谐振网络的ECPT系统的参数设计方法，包括如下步骤：

S1：根据应用场景的需求来确定该系统的工作频率f，耦合单元等效电容C_s以及负载电阻R_L；

S2：根据下面公式计算系统参数：

为了满足参数对称关系，即L₁＝L₂，C₁＝C₂；

所述谐振电感式中，k₁＝k₂＝k，k₁＝C₁/C_s，k₂＝C₂/C_s，ω为系统基波角频率；

当时，系统工作于ZPA状态，式中，品质因数Q＝ωL₂/Req，R_eq为等效交流电阻，且R_eq＝8R_L/π²；

所述谐振电容

此外，对正向LCC网络而言，可求得其传递函数为

式中R为正向LCC网络等效负载，ω_x为角频率，其值不小于基波角频率ω。由式公式15可知，当时，|T(jω_x)|随ω_x的增大而减小，且有可见LCC网络能衰减输入电压中的高频成分，具有滤波器的功能。因此，在设计电路时，根据需要选择最低次谐波分量(其角频率为ω_min)，并确定与之对应的电压幅值增益上限k_min，即|T(jω_min)|≤k_min≤|T(jω)|，也即解得

可见，角频率不低于ω_min的电压谐波分量的幅值增益均不会大于k_min，这样就确保了LCC电路具有良好的滤波性能。系统参数设计流程图如图2所示，图中为系统全谐振条件下，得到的系统工作频率与各参数应满足的条件，为第4节中频闪映射建模所得。

最后，利用不动点函数方程对参数进行验证。

下面将通过频闪映射建模，来分析系统各参数在一定范围内变化时，对系统谐振工作点的影响。

首先，建立系统状态空间模型：

以文献Chun Sen Tang,Yue Sun,Yu Gang Su,Sing Kiong Nguang,and Aiguo Patrick Hu.Determining Multiple Steady-State ZCS Operating Points of a Switch-Mode Contactless Power Transfer System[J].2009,24(2):416-425中软开关不动点理论对谐振频率的分析方法为基础，建立系统状态空间模型。基于参数互补对称式LCC的ECPT系统实际电路原理图如图4所示，图中和分别为L₁、L₂和C_s的等效串联电阻，由于和与绕制电感的绕线材料及长度等众多因素有关，并无通用公式对其值进行直接计算，故本实施例只做测量近似等效。R_Cs＝tanδ/(2πfC_s)，tanδ为介质损耗角正切值。

以电感电流和电容电压为变量，采用基尔霍夫电压定律和电流定律对图3所示电路列写微分方程：

令x＝[i₁ u₁ u₂ u_s i₂]^T为该系统的状态向量,u＝[u_i]为该系统的输入向量，则由微分方程模型(17)可得ECPT系统的状态空间模型：

式中，

接着，建立系统频闪映射模型：

现对图4所示ECPT系统精确模型建立频闪映射模型，将建立的状态空间模型(18)分段线性化为两个模态：

模态1：开关管S₁和S₄导通，开关管S₂和S₃关断，系统的输入变量u_i＝E；

模态2：开关管S₁和S₄关断，开关管S₂和S₃导通，系统的输入变量u_i＝-E；

两个模态的持续时间分别为半个周期T/2，在模态1和模态2下该系统的状态映射函数如下：

假设第n个稳态周期的初始状态为x_n，第n个稳态周期的结束状态为x_n+1，当系统处于稳态时，系统的状态向量周期性的重复，即有x_n+1＝x_n，可以得到系统第n个稳态周期的频闪映射模型：

进而得到系统的稳态周期不动点x^*：

式中，Φ(t)＝e^At，定义Y＝[1 0 0 0 0]为系统的状态选择矩阵，从状态向量x^*中取出开关电流分量，即为流过电感L₁的逆变器输出电流。如果设置周期T为变量，那么系统的周期不动点x^*就可以认为是周期T的函数。取出不动点x^*中的电流分量，就可以得到用于分析谐振软开关工作点的系统周期不动点函数：

按照表1所示参数带入式(22)，得到系统周期不动点函数的时间曲线如图5所示，可见系统有多个谐振软开关工作点，即

有多个非零解。由文献Chun Sen Tang,Yue Sun,Yu Gang Su,Sing Kiong Nguang,and Aiguo Patrick Hu.Determining Multiple Steady-State ZCS Operating Points of a Switch-Mode Contactless Power Transfer System[J].2009,24(2):416-425可知应取第一个过零点作为系统谐振工作点，系统处于基波全谐振状态。

表1系统精确模型参数

在实际应用中，一般要求耦合极板可以有一定的偏移，同时谐振电感和电容受外部不确定因素影响也会发生微小变化，对鲁棒性较差的高阶系统来说，这些变化可能导致系统工作不稳定甚至崩溃。对于本发明所提出的ECPT系统，通过求解系统谐振工作点函数方程(23)，即可得到系统谐振软开关工作点随各参数的变化曲线，即系统参数鲁棒性曲线。分别将式(23)中的R_eq、C_s、L₁(L₂)和C₁(C₂)设置为变量，分别得到谐振工作点随上述参数变化如图6(a)-图6(d)所示。

由图6(a)可知，当R_eq小于14Ω时，出现频率分叉现象，在这种情况下，系统将处于不稳定状态。当R_eq大于14Ω时，可以看到系统处于比较稳定的状态，其工作频率基本不受R_eq的影响。由图6(b)可知，当耦合极板电容在(10pF，50pF)之间变化时，谐振频率在(495.8kHz，507.1kHz)之间变化，可见C_s在增大或减小67％时，谐振频率最大变化1.42％，说明C_s在上述范围内的变化，对谐振频率影响较小，系统仍能稳定工作。图6(c)和图6(d)所示为谐振电感和电容变化对系统谐振工作点的影响，可见其一定程度的变化对系统谐振性能影响较小。

综合上述分析可知本发明所提出的基于参数互补对称式LCC谐振网络的ECPT系统对系统参数鲁棒性较好，参数在一定范围内变化时系统传输性能仍然较好。

基于以上参数设计方法和谐振软开关工作点分析过程，在MATLAB/Simulink环境下建立系统仿真模型，仿真参数如表1所示。图7所示为逆变输出电压和电流，可见系统工作在ZPA状态下，即系统处于全谐振状态，确保逆变器具有较高的功率因数。图8所示为逆变器输出电压和耦合极板激励电压的曲线关系，可以看出电压提升约50倍，满足式(11)给出的大小关系。图9为负载在20Ω、40Ω和60Ω之间切换时通过负载的电流波形，可见系统输出电流基本保持不变，即系统表现出恒流输出特性。

基于以上分析，本实验在42V直流输入的情况下，以30pF耦合极板容值传输110W功率。耦合机构由两对四块50cm×50cm金属板构成，极板间距约为4.3cm，每对极板构成一个耦合电容。耦合电容大小根据如下公式：

C_s1＝[1+2.343(d/l)^0.891]·(εl²/d) (24)

可以得到C_s1＝65pF，式中，d为每对耦合极板之间的距离，l为耦合极板边长，ε＝8.85×10^-12F/m，为真空介电常数。现以表2所示参数作为实验参数，对本发明所提系统特性进行验证，其中电感、电容和电阻均为电桥实测参数。实验中开关频率稍高于系统谐振频率，以使系统在给定参数下能工作于ZVS状态，减小了开关管损耗。

表2系统实验参数

图10所示为逆变输出电压和电流波形，可见在开关管开通前，其电压已下降到零，从而实现ZVS，减小了开关管损耗。图11所示为逆变输出电压和耦合极板激励电压，可见其升压在50倍左右，升压效果较好，与仿真一致性较好。图12所示为激励电压和负载拾取电压，其降压效果明显，且两者基本处于同相位，其偏差主要由于工作频率稍大于系统固有谐振频率导致，与理论分析一致。

为获得合适的输出功率和传输效率，现对耦合电容影响系统输出功率和传输效率的规律进行分析。系统损耗主要包括电感等效串联电阻损耗、耦合极板等效串联电阻损耗以及开关器件损耗，耦合电容的变化会直接影响系统输出功率和传输效率。以(10pF，50pF)作为耦合电容变化范围，实验分别得到系统输出功率P_out和传输效率η随耦合电容的变化规律曲线如图13所示。图中可以发现，在(30pF，35pF)之间，C_s越小时，P_out反而越大，是因为C_s越小，k越大，输入端到C₂端的升压倍数增大，负载端接收到的电压也就越大，所以传输功率增大。但如果C_s继续减小，系统将失谐将会比较严重，开关管损耗大大增加，所以传输功率下降。

对于本ECPT系统，当C_s在(25pF，35pF)之间时，负载能获得合适的输出功率，同时，传输效率也很可观。

本申请的上述实例中，通过提供一种对称式LCC谐振网络的ECPT系统及其参数设计方法，包括直流电源、高频逆变电路、LC谐振网络、由两对耦合极板构成的耦合单元、CL谐振网络、整流滤波电路以及负载R_L，其中，LC谐振网络与耦合极板等效电容C_s构成正向LCC谐振网络，通过对正向LCC谐振网络的参数设计保证了正向LCC谐振网络的恒压输出，CL谐振网络与C_s构成反向LCC谐振网络，结合反向LCC谐振网络的对称参数设计，保证系统耦合极板激励电压到负载电压的降压比例灵活可调，本发明在不需要大幅度增加系统频率和串联补偿电感的条件下，就可以实现传输距离大、传输效率高的效果，同时也提高了系统鲁棒性，提升了系统功率密度，降低了应用成本。

应当指出的是，上述说明并非是对本发明的限制，本发明也并不仅限于上述举例，本技术领域的普通技术人员在本发明的实质范围内所做出的变化、改性、添加或替换，也应属于本发明的保护范围。