一种配电网大面积停电快速恢复最优路径选取方法与流程

本发明涉及配电自动化领域，尤其涉及一种配电网大面积停电快速恢复最优路径选取方法

背景技术：

目前，配电网在运行过程中，当110kv变电站发生因进线或母线发生故障时，导致变电站全停时，配电网会生成大面积停电，如何快速恢复供电区域的负荷成为配电网调度的首要问题。

依靠配电自动化系统把故障快速隔离后，就可以把停电负荷通过网络转移出去，常规的方法是把负荷转移到对侧，如果转移过去会导致主变或线路过载，则减少转移负荷量，使其满足过载约束。

配电自动化能够在分钟级别同时完成非故障区恢复供电的任务，其执行效率远远高于现场人工合联络开关，配电自动化能够大大缩短大面积停电时非故障区快速复电的时间，充分发挥配电自动化优势成为配电网调度人员努力的方向。

常规的大面积停电恢复供电算法主要以恢复供电最大量为目标，没有充分发挥配电自动化的优势，即没有考虑整个恢复方案执行时间问题，从而使得计算出来的供电路径有时因执行时间过长而造成用户停电时间过长，使得企业经济效益受损。存在着恢复方案执行时间过长等弊端。

技术实现要素：

有鉴于此，本发明提供了一种配电网大面积停电快速恢复供电方法，以实现最短的时间内恢复最大量的负荷。为实现上述目的，本发明采取以下技术方案：

一种配电网大面积停电快速恢复供电方法，其特征在于包括以下步骤：

(1)对停电变电站每条馈线进行处理，采集与停电前负荷，并识别其所属类型：

a.单路径馈线：馈线只有一条恢复路径；

b.多路径馈线：馈线有多于一条的恢复路径；

(2)收集各路径所关联的母线、变电站、主变，计算转供线路的裕度及主变裕度参数。

(3)进行第一阶段单路径馈线恢复计算，对恢复负荷和限额进行设置，建立安全运行约束，安全运行约束包括线路传输限额约束及主变限额约束，数学表达如下：

(3.1)线路限额约束

xi≤min(ri(1-ai),kli)(1)

式(1)中,xi为单路径馈线i的待恢复负荷量，0<xi,ri为转移侧的线路容量，ai为转移侧实际负载率，li为失电前馈线i的负荷量，k为负荷波动因子，其中0<k,表示负荷波动系数。

(3.2)主变限额约束

式中：ω1为转移到同一台主变上的所有单路径停电馈线的组合，ti为转移到同一台主变的限额，限额由运行方式所确定，bi为转移前主变的负载率。

(4)建立以单路径馈线最优解为目标的数学模型表达；所述数学模型表达建立在以下假设基础上：

a.研究的各停电馈线未来一段时间内的负荷波动是相同的。

b.对于三双接线的馈线认为其停电前的负荷就是其恢复后的负荷，不考虑因送电时间差异所导致的两条馈线间的负荷转移；

c.不考虑停电变电站母线间的运行方式。

所述第一阶段数学模型表达的初始目标函数如下：

式中：xi代表单路径馈线i上所能恢复的负荷，n为单路径馈线的数量，f为停电变电站所能恢复的最大负荷量

对约束条件进行松弛，引入松弛变量将函数不等式约束化为等式约束；

式(1)、(2)可转换成如下形式：

xi+x′i＝min(ri(1-ai),kli)(4)

式中：x′i，x″i分别为对应xi与ti的松驰变量；

最终将第一阶段目标函数转化成：

其中m为转移主变的数量

(6)建立数学模型后，以x′i，x″i作为数学模型的基变量，得到一个单位矩阵，令非基变量为0，得到初始基可行解，利用单纯形法进行迭代，求出目标函数最大值，由于矩阵列向量均为非零向量，故有最优解。

(7)把最优解作为供电恢复第一阶段目标，把第一阶段执行结果作为第二阶段的初始状态，建立第二阶段运行约束，数学表达示如下：

(7.1)线路负荷时效限额约束

wjxj≤min(rj(1-aj),klj)(7)

其中xj为多路径馈线转移的所能恢复的负荷量，wi为负荷转移时间系数，rj转移侧的线路容量，aj为转移侧目前的负载率，lj失电前馈线j的负荷量。

wj计算公式如下：

其中，u为负荷转移路径需要的联络开关数量，k为此条转移路径的每一个联络开关，ck为此联络开关闭合所花费的时间，ck可以取标幺值，其基础量纲可根据实际设置。

(7.2)主变限额约束，

其中，ω2为转移到同一台主变上的所有多路径停电馈线的组合，tj为转移到同一台主变的限额，限额由运行方式所确定，bj为第一阶段转移后主变的负载率。

(8)建立多路径馈线最优解为目标的数学模型表达；所述数学模型表达建立在以下假设基础上：

a.不同多路径馈线可以转移到同一台主变；

b.一条多路径馈线转移路径至少有两条；

c.一条多路径馈线的可转移路径不能同时出现在一个数学模型中。

d.所有的多路径馈线必须在一个数据模型中。

所述数学模型表达的初始目标函数如下：

式中：xj代表多路径馈线j上所能恢复的负荷，d为多路径馈线的数量，f'为停电变电站所能恢复的最大负荷量

对约束条件进行松弛，引入松弛变量将函数不等式约束(7)和(9)化为等

式约束wjxj+x'j＝min(rj(1-aj),klj)(11)

其中x'j，x″j分别为对应xj与tj的松驰变量；

最终将第二阶段目标函数转化成

其中q为转移主变的数量。

(9)选择多路径转移方案，转移方案生成规则如下：

a.在每一次方案生成时，一条多路径馈线只能从其可行的转移方案中选择一种；

b.所有的多路径馈线在每一次方案生成时，都必须选择一次；

c.每种选择方案至少有一条转移路径与其它方案不同；

(10)对每一种转移方案，应用单纯形法求解第二阶段目标函数值。

(11)对转移方案的目标函数值进行比较，选择最大值，把方案加入优选方案集。

本发明的有益效果是：提出一种配电网大面积停电快速恢复最优路径选取方法，此方法有效兼顾最大恢复负荷量与最短恢复时间之间的平衡，能够充分现有网架的网络转供能力，并充分发挥配电自动化系统在恢复供电方案的优势，使得选出的最优路径更具有可操作性。

附图说明

图1是本发明的流程图；

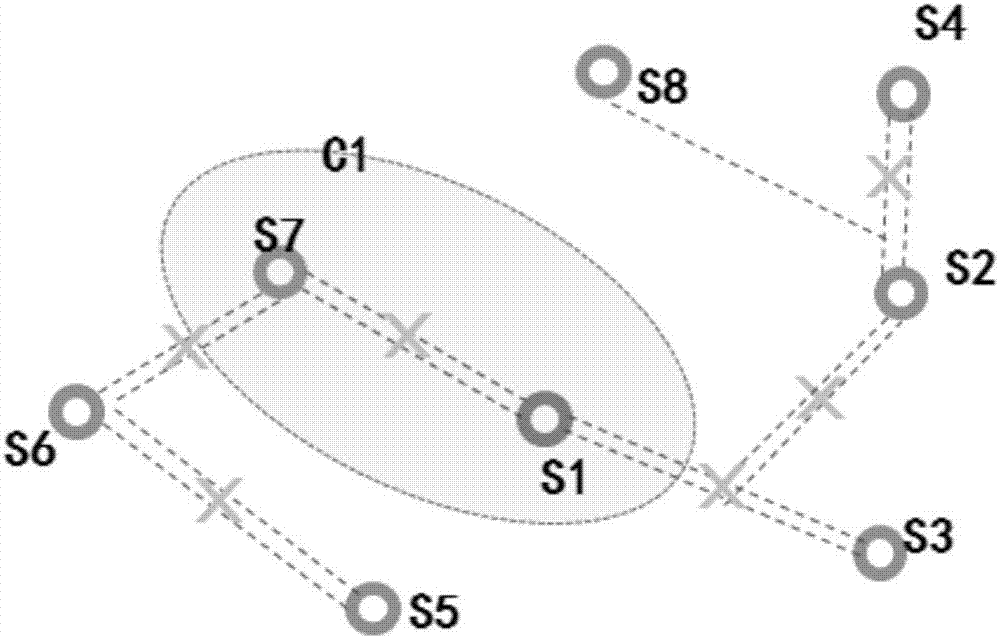
图2是单路径馈线示意图；

图3是多路径馈线示意图。

具体实施方式

下面结合附图和具体实施例对本发明作进一步详细说明。

图1给出了配电网大面积停电快速恢复最优路径选择方法。其中

f1:识别停电馈线路径，对停电变电站每条馈线进行处理，采集与停电前负荷，并识别其所属类型：

a.单路径馈线：馈线只有一条恢复路径；

b.多路径馈线：馈线有多于一条的恢复路径；

所述的单路径馈线见图2中的c1椭圆形区域所包括的馈线。

所述的多路径馈线见图3中的c2椭圆形区域所包括的馈线

f2:收集计算参数，包括各路径所关联的母线、变电站、主变，计算转供线路的裕度及主变裕度参数。

f3：进行第一阶段单路径馈线恢复计算，对恢复负荷和限额进行设置，建立安全运行约束，安全运行约束包括线路传输限额约束及主变限额约束，数学表达如下：

(3.1)线路限额约束

xi≤min(ri(1-ai),kli)(1)

式(1)中,xi为单路径馈线i的待恢复负荷量，0<xi,ri为转移侧的线路容量，ai为转移侧实际负载率，li为失电前馈线i的负荷量，k为负荷波动因子，其中0<k,表示负荷波动系数。

(3.2)主变限额约束

式中：ω1为转移到同一台主变上的所有单路径停电馈线的组合，ti为转移到同一台主变的限额，限额由运行方式所确定，bi为转移前主变的负载率。

(3.3)建立以单路径馈线最优解为目标的数学模型表达；所述数学模型表达建立在以下假设基础上：

a.研究的各停电馈线未来一段时间内的负荷波动是相同的。

b.对于三双接线的馈线认为其停电前的负荷就是其恢复后的负荷，不考虑因送电时间差异所导致的两条馈线间的负荷转移；

c.不考虑停电变电站母线间的运行方式。

所述第一阶段数学模型表达的初始目标函数如下：

式中：xi代表单路径馈线i上所能恢复的负荷，n为单路径馈线的数量，f为停电变电站所能恢复的最大负荷量

对约束条件进行松弛，引入松弛变量将函数不等式约束化为等式约束；

式(1)、(2)可转换成如下形式：

xi+x′i＝min(ri(1-ai),kli)(4)

式中：x′i，x″i分别为对应xi与ti的松驰变量；

最终将第一阶段目标函数转化成：

其中m为转移主变的数量

(3.4)建立数学模型后，以x′i，x″i作为数学模型的基变量，得到一个单位矩阵，令非基变量为0，得到初始基可行解，利用单纯形法进行迭代，求出目标函数最大值，由于矩阵列向量均为非零向量，故有最优解。

f4:修改第二阶段计算参数，把最优解作为供电恢复第一阶段目标，把第一阶段执行结果作为第二阶段的初始状态。建立第二阶段运行约束，数学表达示如下：

(4.1)线路负荷时效限额约束

wjxj≤min(rj(1-aj),klj)(7)

其中xj为多路径馈线转移的所能恢复的负荷量，wi为负荷转移时间系数，rj转移侧的线路容量，aj为转移侧目前的负载率，lj失电前馈线j的负荷量。

wj计算公式如下：

其中，u为负荷转移路径需要的联络开关数量，k为此条转移路径的每一个联络开关，ck为此联络开关闭合所花费的时间，若为自动化开关，其取值为2，若为非自动化开关，其取值为16.

(4.2)主变限额约束，

其中，ω2为转移到同一台主变上的所有多路径停电馈线的组合，tj为转移到同一台主变的限额，限额由运行方式所确定，bj为第一阶段转移后主变的负载率。

(4.3)建立多路径馈线最优解为目标的数学模型表达；所述数学模型表达建立在以下假设基础上：

a.不同多路径馈线可以转移到同一台主变；

b.一条多路径馈线转移路径至少有两条；

c.一条多路径馈线的可转移路径不能同时出现在一个数学模型中。

d.所有的多路径馈线必须在一个数据模型中。

所述数学模型表达的初始目标函数如下：

式中：xj代表多路径馈线j上所能恢复的负荷，d为多路径馈线的数量，f'为停电变电站所能恢复的最大负荷量

对约束条件进行松弛，引入松弛变量将函数不等式约束(7)和(9)化为等

式约束wjxj+x'j＝min(rj(1-aj),klj)(11)

其中x'j，x″j分别为对应xj与tj的松驰变量；

最终将第二阶段目标函数转化成

其中q为转移主变的数量。

f5：识别可选方案，可选方案生成规则如下：

a.在每一次方案生成时，一条多路径馈线只能从其可行的转移方案中选择一种；

b.所有的多路径馈线在每一次方案生成时，都必须选择一次；

c.每种选择方案至少有一条转移路径与其它方案不同；

f6：对每个可选方案进行第二阶段计算。对每个可选方案应用单纯形法求解第二阶段目标函数值。

f7：判断是否所有的可选方案都完成第二阶段目标函数值的计算，如果没有完成，则继续执行s6

f8：对所有可选方进行排序。排序时的主要依据第二阶段目标函数值的大小，如以图3中的s1变电站发生全停，多选路径有s1->s2,s1->s3两条多路径方案。

如果s1->s2和s1->s3联络开关均为自动化开关，并且都能够满足运行约束，则它们都属于最优方案，如果s1->s2联络开关属于自动化开关，而s1->s3中的联络开关属于需要人工现场合闸的非自动化开关，则s1->s2目标函数值将超过s1->s3目标函数值，s1->s2则为最优方案。

f9：选择最优路径，把最大目标函数值的所有路径加入优选方案集做为最优路径。

本发明的有益效果是：提出一种配电网大面积停电快速恢复最优路径选取方法，此方法有效兼顾最大恢复负荷量与最短恢复时间之间的平衡，能够充分现有网架的网络转供能力，并充分发挥配电自动化系统在恢复供电方案的优势，使得选出的最优路径更具有可操作性。